2021暑期小升初数学衔接班课件第4讲有理数的加减法(19张PPT)
文档属性
| 名称 | 2021暑期小升初数学衔接班课件第4讲有理数的加减法(19张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 3.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-27 21:50:10 | ||
图片预览






文档简介
主讲教师:数学老师
2021/小升初数学/总复习/专题复习/教学课件
考点梳理
Knowledge network
01
考点解析
Question type analysis
02
课时训练
Real exercise
03
知识小结
Knowledge summary
04
教学目标:
1,经历探索有理数加法法则的过程,并会根据有理数的加法法则进行有理数的加法运算。
2,经历有理数加法运算律的探索过程,并能用运算律简化有理数加法的运算.
3,掌握有理数减法法则并熟练地进行有理数减法运算。
4,理解有理数的加减法法可以互相转化,熟练地进行有理数的加减混合运算。
教学重点:了解有理数的加法的意义,会根据有理数的加法法则进行有理数的加法运算。
教学难点:有理数加法中的异号两数如何进行加减法运算。
一、创设问题情境,引入新课
(1)计算:2+8= ,+7+8= .
(2)思考:7+(-13)如何计算?
10
15
这涉及到正数和负数的加法。从这节课开始我们就来学习有理数的运算——加法运算。
二、讲授新课:
(一)借助数轴来讨论有理数的加法
1)如果规定向东为正,向西为负,那么一个人向东走4米,再向东走2米,两次共向东走了 米,这个问题用算式表示就是: .
6
(+4)+(+2)=+6
2)如果规定向东为正,向西为负,那么一个人向西走2米,再向西走4米,两次共向西走多少米?很明显,两次共向西走了 米.
这个问题用算式表示就是: .
如图所示:
6
(-4)+(-2)=-6
3)如果向西走2米,再向东走4米, 那么两次运动后,这个人从起点向东走了 米,
写成算式就是 这个问题用数轴表示如下图所示:
2
(-2)+(+4)=+2
4)利用数轴,求以下情况时这个人两次运动的结果:
先向东走3米,再向西走5米,这个人从起点向( )走了( )米;
先向东走5米,再向西走5米,这个人从起点向( )走了( )米;
先向西走5米,再向东走5米,这个人从起点向( )走了( )米。
写出这三种情况运动结果的算式
.
.
.
3十(一5)= 一2
5十(一5)= 0
(一5)十5 = 0
5)如果物体第1秒向右(或向左)运动5m,第2秒原地不动,两秒后物体从起点向 (或 )运动了 m。
启发学生或由教师写出对应的算式:
,
你能从以上算式中发现有理数的加法运算法则吗?
有理数的加法法则:
5十0 = 5 或(一5)十0 = 一5
右(或左)运动5m.
(1)同号两数相加,取相同的符号,并把绝对值相加;
(2)绝对值不相等的异号两数相加,取绝对值较大的加数的符号,并用较大的绝对值减去较小的绝对值,互为相反数的两个数相加得0;
(3)一个数同0相加,仍得这个数。
精讲点拨:
例1.计算:(1)(一5)十(一8)
(2)(一4.9)十3.7.
解:(1)(一5)十(一8)=-(5+8)=-13;
(2)(一4.9)十3.7=-(4.9-3.7)=-1.2.
跟踪练习:
计算:(1)15十(一22);(2)(一13)十(一8);
(3)(一0.9)十1.5;
解:(1)15十(一22)=一(22一15)=一7
(2)(一13)十(一8)= 一(13十8)=一21
(3)(一0.9)十1.5=十(1.5一0.9)=0.6
(二)探究利用运算律进行有理数的加法简便计算
计算:30 +(-20)和 (-20)+30.
[ 8 +(-5)] +(-4)和 8 + [(-5)+(-4)].
思考:观察上面的式子与计算结果,你有什么发现?
30 +(-20)=10,(-20)+30=10. 30 +(-20)=(-20)+30.
[ 8 +(-5)] +(-4)=3+(-4)=-1, 8 + [(-5)+(-4)]= 8 +(-9)=-1.
[ 8 +(-5)] +(-4)= 8 + [(-5)+(-4)].
由上可以知道,小学学习的加法交换律、结合律在有理数范围内同样适应,即:两个数相加,交换加数的位置,和 .式子表示为 .
三个数相加,先把前两个数相加,或者先把后两个数相加,和 .
用式子表示为 .
不变
不变
a+b=b+a
(a+b)+c= a+(b+c)
精讲点拨:
例2, 计算:(1)16 +(-25)+ 24 +(-35)
(2)(—2.48)+(+4.33)+(—7.52)+(—4.33)
解:(1)16 +(-25)+ 24 +(-35)
=16 + 24 +(-25)+(-35)
=40-60
=-20;
(2)(—2.48)+(+4.33)+(—7.52)+(—4.33)
=(—2.48)+(—7.52)(+4.33)+(—4.33)
=-10+0
=-10.
(三)探究有理数的减法法则
计算:(1)9一8,9十(一8);
(2)15一7,15十(一7)
思考:观察上面的式子与计算结果,你有什么发现?
9-8=1,9+(-8)=1,9-8=9+(-8),
15一7=8,15十(一7)=8,15一7=15十(一7).
师生总结出减法法则: ,
用字母表示为: .
在此过程中有两个转化必须同时进行,即当把减号变为 号时,减数必须变为原来的 。
减去一个数,等于加这个数的相反数
加
相反数
精讲点拨:
例1. 计算:(1)一7一(一4); (2)0一9;
(3)6.2一(一3.8);
解:(1)-7-(-4)=-7+4=-3,
(2)0一9=0+(-9)=-9;
(3)6.2一(一3.8)=6.2+3.8=10.
跟踪练习:
计算:(1)﹣5﹣(﹣9); (2)|﹣15|﹣(﹣2);
解:(1)﹣5﹣(﹣9)=﹣5+9=4;
(2)|﹣15|﹣(﹣2)=15+2=17;
探究:有理数的加减混合运算
1.思考:利用有理数的加减法法则把下式改写成省略加号和括号的形式
(一20)十(十3)一(一5)一(十7).
解:(一20)十(十3)一(一5)一(十7)=一20十3十5一7.
2.如何利用运算律可将一5.13十4.62十(一8.47)一(一2.38)简便计算?
解:一5.13十4.62十(一8.47)一(一2.38)
=一5.13十4.62一8.47+2.38
=(一5.13一8.47)+(4.62+2.38)
=-13.5+7
=-6.5.
归纳总结:1.先把算式改写成省略加号和括号的形式2.利用交换律把同号、同分母以及相同形式的数放到一起,然后利用结合律结合,3.利用加减法法则计算即可.
自主练习:(1)(—7)—(+5)+(—4)—(—10);
(2)27—18+(—7)—32 .
解:(—7)—(+5)+(—4)—(—10)= —7—5—4+10=-16+10=-6;
(2)27—18+(—7)—32=27—18—7—32=--30 .
(五)课时小结:
这节课我们主要学习了哪些内容?
1.有理数的加法法则:
(1)同号两数相加,取相同的符号,并把绝对值相加;
(2)绝对值不相等的异号两数相加,取绝对值较大的加数的符号,并用较大的绝对值减去较小的绝对值,互为相反数的两个数相加得0;
(3)一个数同0相加,仍得这个数。
2. 在进行有理数数的加法运算时,先确定符号,再算绝对值.
3.有理数的减法法则,会利用法则进行有理数的减法计算.
4.利用运算律进行有理数的加减混合运算.
主讲教师:数学老师
2021/小升初数学/总复习/专题复习/教学课件
谢谢观赏
21世纪教育网(www.21cnjy.com)中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
2021/小升初数学/总复习/专题复习/教学课件
考点梳理
Knowledge network
01
考点解析
Question type analysis
02
课时训练
Real exercise
03
知识小结
Knowledge summary
04
教学目标:
1,经历探索有理数加法法则的过程,并会根据有理数的加法法则进行有理数的加法运算。
2,经历有理数加法运算律的探索过程,并能用运算律简化有理数加法的运算.
3,掌握有理数减法法则并熟练地进行有理数减法运算。
4,理解有理数的加减法法可以互相转化,熟练地进行有理数的加减混合运算。
教学重点:了解有理数的加法的意义,会根据有理数的加法法则进行有理数的加法运算。
教学难点:有理数加法中的异号两数如何进行加减法运算。
一、创设问题情境,引入新课
(1)计算:2+8= ,+7+8= .
(2)思考:7+(-13)如何计算?
10
15
这涉及到正数和负数的加法。从这节课开始我们就来学习有理数的运算——加法运算。
二、讲授新课:
(一)借助数轴来讨论有理数的加法
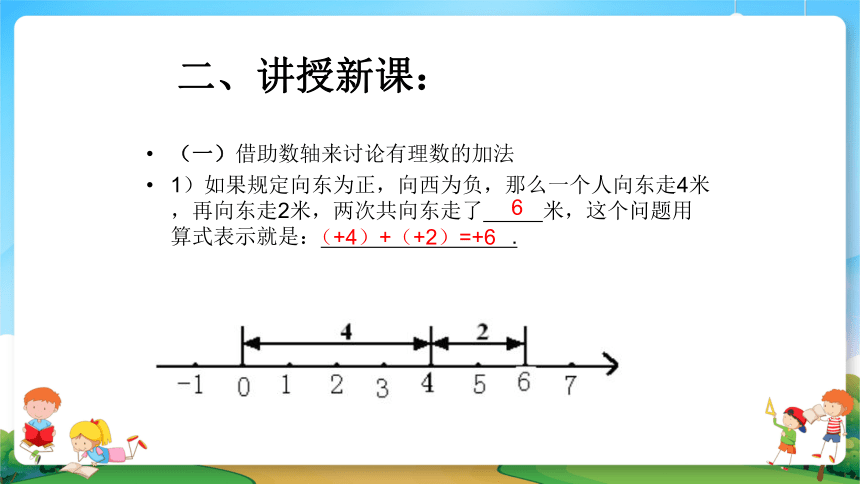
1)如果规定向东为正,向西为负,那么一个人向东走4米,再向东走2米,两次共向东走了 米,这个问题用算式表示就是: .
6
(+4)+(+2)=+6
2)如果规定向东为正,向西为负,那么一个人向西走2米,再向西走4米,两次共向西走多少米?很明显,两次共向西走了 米.
这个问题用算式表示就是: .
如图所示:
6
(-4)+(-2)=-6
3)如果向西走2米,再向东走4米, 那么两次运动后,这个人从起点向东走了 米,
写成算式就是 这个问题用数轴表示如下图所示:
2
(-2)+(+4)=+2
4)利用数轴,求以下情况时这个人两次运动的结果:
先向东走3米,再向西走5米,这个人从起点向( )走了( )米;
先向东走5米,再向西走5米,这个人从起点向( )走了( )米;
先向西走5米,再向东走5米,这个人从起点向( )走了( )米。
写出这三种情况运动结果的算式
.
.
.
3十(一5)= 一2
5十(一5)= 0
(一5)十5 = 0
5)如果物体第1秒向右(或向左)运动5m,第2秒原地不动,两秒后物体从起点向 (或 )运动了 m。
启发学生或由教师写出对应的算式:
,
你能从以上算式中发现有理数的加法运算法则吗?
有理数的加法法则:
5十0 = 5 或(一5)十0 = 一5
右(或左)运动5m.
(1)同号两数相加,取相同的符号,并把绝对值相加;
(2)绝对值不相等的异号两数相加,取绝对值较大的加数的符号,并用较大的绝对值减去较小的绝对值,互为相反数的两个数相加得0;
(3)一个数同0相加,仍得这个数。
精讲点拨:
例1.计算:(1)(一5)十(一8)
(2)(一4.9)十3.7.
解:(1)(一5)十(一8)=-(5+8)=-13;
(2)(一4.9)十3.7=-(4.9-3.7)=-1.2.
跟踪练习:
计算:(1)15十(一22);(2)(一13)十(一8);
(3)(一0.9)十1.5;
解:(1)15十(一22)=一(22一15)=一7
(2)(一13)十(一8)= 一(13十8)=一21
(3)(一0.9)十1.5=十(1.5一0.9)=0.6
(二)探究利用运算律进行有理数的加法简便计算
计算:30 +(-20)和 (-20)+30.
[ 8 +(-5)] +(-4)和 8 + [(-5)+(-4)].
思考:观察上面的式子与计算结果,你有什么发现?
30 +(-20)=10,(-20)+30=10. 30 +(-20)=(-20)+30.
[ 8 +(-5)] +(-4)=3+(-4)=-1, 8 + [(-5)+(-4)]= 8 +(-9)=-1.
[ 8 +(-5)] +(-4)= 8 + [(-5)+(-4)].
由上可以知道,小学学习的加法交换律、结合律在有理数范围内同样适应,即:两个数相加,交换加数的位置,和 .式子表示为 .
三个数相加,先把前两个数相加,或者先把后两个数相加,和 .
用式子表示为 .
不变
不变
a+b=b+a
(a+b)+c= a+(b+c)
精讲点拨:
例2, 计算:(1)16 +(-25)+ 24 +(-35)
(2)(—2.48)+(+4.33)+(—7.52)+(—4.33)
解:(1)16 +(-25)+ 24 +(-35)
=16 + 24 +(-25)+(-35)
=40-60
=-20;
(2)(—2.48)+(+4.33)+(—7.52)+(—4.33)
=(—2.48)+(—7.52)(+4.33)+(—4.33)
=-10+0
=-10.
(三)探究有理数的减法法则
计算:(1)9一8,9十(一8);
(2)15一7,15十(一7)
思考:观察上面的式子与计算结果,你有什么发现?
9-8=1,9+(-8)=1,9-8=9+(-8),
15一7=8,15十(一7)=8,15一7=15十(一7).
师生总结出减法法则: ,
用字母表示为: .
在此过程中有两个转化必须同时进行,即当把减号变为 号时,减数必须变为原来的 。
减去一个数,等于加这个数的相反数
加
相反数
精讲点拨:
例1. 计算:(1)一7一(一4); (2)0一9;
(3)6.2一(一3.8);
解:(1)-7-(-4)=-7+4=-3,
(2)0一9=0+(-9)=-9;
(3)6.2一(一3.8)=6.2+3.8=10.
跟踪练习:
计算:(1)﹣5﹣(﹣9); (2)|﹣15|﹣(﹣2);
解:(1)﹣5﹣(﹣9)=﹣5+9=4;
(2)|﹣15|﹣(﹣2)=15+2=17;
探究:有理数的加减混合运算
1.思考:利用有理数的加减法法则把下式改写成省略加号和括号的形式
(一20)十(十3)一(一5)一(十7).
解:(一20)十(十3)一(一5)一(十7)=一20十3十5一7.
2.如何利用运算律可将一5.13十4.62十(一8.47)一(一2.38)简便计算?
解:一5.13十4.62十(一8.47)一(一2.38)
=一5.13十4.62一8.47+2.38
=(一5.13一8.47)+(4.62+2.38)
=-13.5+7
=-6.5.
归纳总结:1.先把算式改写成省略加号和括号的形式2.利用交换律把同号、同分母以及相同形式的数放到一起,然后利用结合律结合,3.利用加减法法则计算即可.
自主练习:(1)(—7)—(+5)+(—4)—(—10);
(2)27—18+(—7)—32 .
解:(—7)—(+5)+(—4)—(—10)= —7—5—4+10=-16+10=-6;
(2)27—18+(—7)—32=27—18—7—32=--30 .
(五)课时小结:
这节课我们主要学习了哪些内容?
1.有理数的加法法则:
(1)同号两数相加,取相同的符号,并把绝对值相加;
(2)绝对值不相等的异号两数相加,取绝对值较大的加数的符号,并用较大的绝对值减去较小的绝对值,互为相反数的两个数相加得0;
(3)一个数同0相加,仍得这个数。
2. 在进行有理数数的加法运算时,先确定符号,再算绝对值.
3.有理数的减法法则,会利用法则进行有理数的减法计算.
4.利用运算律进行有理数的加减混合运算.
主讲教师:数学老师
2021/小升初数学/总复习/专题复习/教学课件
谢谢观赏
21世纪教育网(www.21cnjy.com)中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
同课章节目录
