2021暑期小升初数学衔接班课件第15讲角与角的运算(25张PPT)
文档属性
| 名称 | 2021暑期小升初数学衔接班课件第15讲角与角的运算(25张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-27 22:04:41 | ||
图片预览








文档简介
第15讲角与角的运算
主讲教师:数学老师
2021/小升初数学/总复习/专题复习/教学课件
考点梳理
Knowledge network
01
考点解析
Question type analysis
02
课时训练
Real exercise
03
知识小结
Knowledge summary
04
CONTENTS
目录
教学目标:
1、掌握角的两种定义形式和四种表示方法.
2、会比较角的大小,能估计一个角的大小.
3、认识度、分、秒,会进行度、分、秒间单位互化及角的和、差、倍、分计算.
4、认识角的平分线;熟练掌握用尺规作一个角等于已知角.
教学重点:
角的概念与角的表示方法,角的大小比较方法,度、分、秒间单位互化及角的和、差、倍、分计算.用尺规作一个角等于已知角.
教学难点:
正确地表示角,度、分、秒间单位互化及角的和、差、倍、分计算.
一、复习旧知
小学中我们已经认识了角,学过哪些关于角的知识?
下面我们更加详细地研究角的有关知识.
二、探求新知
(一)角的概念
1、在学生充分发表自己对角的认识的基础上,师生共同归纳得出:
有公共端点的两条射线组成的图形叫做角,这个公共端点是角的顶点,这两条射线是角的两条边。
2、下面的三个图形是角吗?
不是,因为不符合角的定义,即有公共端点的两条射线组成的图形。
(二)角的表示
我们发现了生活中有许多角的形象.那么,我们如何给这些角取名呢?
有四种方法来表示:
① 用角的两边和角的顶点的字母来表示,如∠AOB,其中O为角的顶点;
② 用角的顶点字母表示,如∠A,其中A为角的顶点;
③ 用数字书写在角的内部来表示,如∠1、∠2等;
④ 用希腊字母来表示,类似于用数字来表示一样,如∠α、∠β等。
(三)用旋转观点定义角
1.思考:在一艘轮船正在大海上打开探照灯寻找目标或一只挂钟的钟摆不停地摆动,在这个过程中,有以新的方式出现的角吗?
探照灯光线移动或钟摆摆动所形成的图形,也可看成是角。
在讨论的基础上,归纳:角也可以看成是由一条射线绕着它的端点旋转而形成的图形。
演示:当射线OA绕点O旋转时,当终止位置OB和起始位置OA成一条线时,会形成什么角?继续旋转,当OB和OA重合时,又形成什么角?
当终止位置OB和起始位置OA成一条线时,会形成平角,也即角的度数为1800,继续旋转,当OB和OA重合时,又形成周角,也即角的度数为3600。
2.把图中的角表示成下列形式,哪些正确,哪些不正确?
(1)∠APO (2)∠AOP
(3)OPC (4)∠OCP
(5)∠O (6)∠P
正确的有:(1)(3)(6)
错误的有:(2)(4)(5)
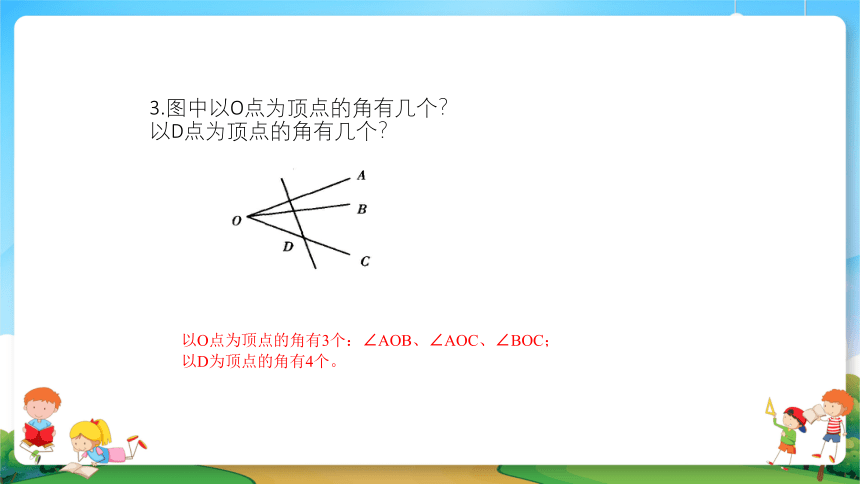
3.图中以O点为顶点的角有几个?
以D点为顶点的角有几个?
以O点为顶点的角有3个:∠AOB、∠AOC、∠BOC;
以D为顶点的角有4个。
(四)度分秒
1.在实际生活中,有时还需要更精密的角度.因此我们把1度的角60等分,每份就是1分的角,记作1′;
把1分的角60等份,每份就是1秒的角,记作1″.
即:1°=60′,1′=60″
归纳:以度、分、秒为单位的角的度量制叫做角度制.
想一想:角度进位制和其他什么进位制相类似?(时间进位制)
2、出示两个问题:
问题1:3.32小时= 3 小时 19 分 12 秒;
3.32度= 3 度 19 分 12 秒。
问题2:12小时9分36秒= 12.16 小时;
12°9′36″= 12.16 度
分组讨论后,请学生回答度、分、秒间的转化方法.
(1)因为计算的时候要将十进制换算成60进制,可将0.32×3600(按照秒计算)得出19.2分,那么0.2分×60得出12秒。故答案为3小时19分12秒。角度由十进制换算成60进制也是同样的道理。
(2)先将秒换算成分,再将分换算成小时。
6秒 = 36 ÷ 60分 = 0.6分 9分 + 0.6分 = 9.6分
9.6分 = 9.6 ÷ 60小时 = 0.16小时 12小时9分36秒 = 12.16小时
师生总结得出:由度化分,由分化秒,只要乘以60即可;由秒化分,由分化l度,只要除以60就行.
例1:计算:
(1)32°21'+68°48';
(2)90°-25°32';
(3)15°23'8”×4.
【答案】
(1)101°9’ (2)64°28’ (3)61°32'32”
【解析】
(1)32°21'+ 68°48'= 100°69’=101°9’
(2)90°- 25°32'= 89°60’- 25°32'= 64°28’
(3)15°23'8”×4 = 60°92'32”= 61°32'32”
练习:计算:
(1)13°29'+78°37',
(2)62°5'-21°39',
(3)107°43'÷5
【答案】
(1)92°6′ (2)40°26′ (3)21°32′36″
【解析】
(1)13°29′+78°37′ = 91°66′= 92°6′
(2)62°5′-21°39′=61°65′-21°39′= 40°26′
(3)107°43′÷5 = 21.4°8.6′=21°32.6′= 21°32′36″
3、平角、周角的度数:
例2:把一个周角8等分,每一份是多少度的角?
每一份角的度数:360°÷ 8 = 45°
(五)角的大小比较
如图已知∠ABC和∠DEF。
请大家讨论一下,用什么方法可以比较这两个角的大小?
分组讨论角的比较方法.在学生讨论过程中,教师深入学生中间巡视,观察并听取他们解决问题的方法和建议.可适当组织交流或分组汇报.师生共同归纳角的比较方法:
(1)度量方法: 用量角器量出角的度数 ,然后比较它们的大小。
(2)叠合方法: 把两个角叠合在一起 比较大小。
2、观察下列图形,图中共有几个角?它们之间有什关系?
3个,∠COB、∠COA、∠BOA;∠COA = ∠COB + ∠BOA
(六)角的平分线问题
问题1:用一副三角尺,你能画出哪些度数的角?
30°、45°、60°、90°;15°、75°、105°、120°、135°、150°。
问题2:在一张纸上画出一个角并剪下,将这个角对折,使其两边重合.想想看,折痕与角两边所成的两个角的大小有什么关系?
相等。折痕与角两边重合,相当于把角平均分成两份,所以两角相等。
由问题2的探讨,引出角的平分线定义及其几何表达式.类似的还有角的三等分线、四等分线等等.想一想,还有什么方法可画出一个角的平分线呢?
一般地,从一个角的顶点出发,把这个角分成两个相等的角的射线,叫做这个角的平分线。
可用量角器平分、尺规作图等方法。
(七)尺规作图
1、画一个角等于已知角,除用量角器外,你还有别的办法吗?
尺规作图法。
2、教师不用量角器和三角尺,而用直尺和圆规来画一个角等于已知∠AOB.
分组讨论:角的顶点和角的一边如何确定?角的另一边怎样画出?画图的关键是什么?
角的顶点和角的一边直接作出即可;角的另一边需要用尺规作图法确定;画图的关键是确定角的另一边上的一个点。
3、教师按课本的步骤边讲边画,学生跟着老师的步骤画.
① 以O点为圆心,适当长为半径作弧,分别交于OA,OB于点C,D;
② 做一条射线O′A′,以点O′为圆心,OC长为半径作弧,交O′A′于点C′;
③ 以点C′为圆心,CD长为半径作弧,交前弧于点D′;
④ 过点O′,D′做射线O′B′;
∠A′O′B′就是所求作的角。
4、已知∠1和∠2如下图所示,用尺规作图画出∠AOB=∠1+∠2,保留作图痕迹
(八)角的计算
例3:已知在平面内,∠AOB=70°,∠BOC=40°,求∠AOC的度数.
【答案】30° 或110°
【解析】
试题分析:∠BOC 可能在∠AOB里边,也可能在∠AOB外边,分情况计算即可。
解:∠BOC在∠AOB里边时,∠AOC = ∠AOB - ∠BOC = 70°- 40° = 30°
∠BOC在∠AOB外边时,∠AOC = ∠AOB + ∠BOC = 70° + 40° = 110°
故答案为30° 或110°。
例4:如图,∠AOB=35°,
∠BOC=90°,
OD是∠AOC 的平分线,
求∠BOD的度数.
三、课堂小结:
这节课你学习了哪些知识?
下课了,谢谢观看
主讲教师:数学老师
2021/小升初数学/总复习/专题复习/教学课件
谢谢观赏
21世纪教育网(www.21cnjy.com)中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
主讲教师:数学老师
2021/小升初数学/总复习/专题复习/教学课件
考点梳理
Knowledge network
01
考点解析
Question type analysis
02
课时训练
Real exercise
03
知识小结
Knowledge summary
04
CONTENTS
目录
教学目标:
1、掌握角的两种定义形式和四种表示方法.
2、会比较角的大小,能估计一个角的大小.
3、认识度、分、秒,会进行度、分、秒间单位互化及角的和、差、倍、分计算.
4、认识角的平分线;熟练掌握用尺规作一个角等于已知角.
教学重点:
角的概念与角的表示方法,角的大小比较方法,度、分、秒间单位互化及角的和、差、倍、分计算.用尺规作一个角等于已知角.
教学难点:
正确地表示角,度、分、秒间单位互化及角的和、差、倍、分计算.
一、复习旧知
小学中我们已经认识了角,学过哪些关于角的知识?
下面我们更加详细地研究角的有关知识.
二、探求新知
(一)角的概念
1、在学生充分发表自己对角的认识的基础上,师生共同归纳得出:
有公共端点的两条射线组成的图形叫做角,这个公共端点是角的顶点,这两条射线是角的两条边。
2、下面的三个图形是角吗?
不是,因为不符合角的定义,即有公共端点的两条射线组成的图形。
(二)角的表示
我们发现了生活中有许多角的形象.那么,我们如何给这些角取名呢?
有四种方法来表示:
① 用角的两边和角的顶点的字母来表示,如∠AOB,其中O为角的顶点;
② 用角的顶点字母表示,如∠A,其中A为角的顶点;
③ 用数字书写在角的内部来表示,如∠1、∠2等;
④ 用希腊字母来表示,类似于用数字来表示一样,如∠α、∠β等。
(三)用旋转观点定义角
1.思考:在一艘轮船正在大海上打开探照灯寻找目标或一只挂钟的钟摆不停地摆动,在这个过程中,有以新的方式出现的角吗?
探照灯光线移动或钟摆摆动所形成的图形,也可看成是角。
在讨论的基础上,归纳:角也可以看成是由一条射线绕着它的端点旋转而形成的图形。
演示:当射线OA绕点O旋转时,当终止位置OB和起始位置OA成一条线时,会形成什么角?继续旋转,当OB和OA重合时,又形成什么角?
当终止位置OB和起始位置OA成一条线时,会形成平角,也即角的度数为1800,继续旋转,当OB和OA重合时,又形成周角,也即角的度数为3600。
2.把图中的角表示成下列形式,哪些正确,哪些不正确?
(1)∠APO (2)∠AOP
(3)OPC (4)∠OCP
(5)∠O (6)∠P
正确的有:(1)(3)(6)
错误的有:(2)(4)(5)
3.图中以O点为顶点的角有几个?
以D点为顶点的角有几个?
以O点为顶点的角有3个:∠AOB、∠AOC、∠BOC;
以D为顶点的角有4个。
(四)度分秒
1.在实际生活中,有时还需要更精密的角度.因此我们把1度的角60等分,每份就是1分的角,记作1′;
把1分的角60等份,每份就是1秒的角,记作1″.
即:1°=60′,1′=60″
归纳:以度、分、秒为单位的角的度量制叫做角度制.
想一想:角度进位制和其他什么进位制相类似?(时间进位制)
2、出示两个问题:
问题1:3.32小时= 3 小时 19 分 12 秒;
3.32度= 3 度 19 分 12 秒。
问题2:12小时9分36秒= 12.16 小时;
12°9′36″= 12.16 度
分组讨论后,请学生回答度、分、秒间的转化方法.
(1)因为计算的时候要将十进制换算成60进制,可将0.32×3600(按照秒计算)得出19.2分,那么0.2分×60得出12秒。故答案为3小时19分12秒。角度由十进制换算成60进制也是同样的道理。
(2)先将秒换算成分,再将分换算成小时。
6秒 = 36 ÷ 60分 = 0.6分 9分 + 0.6分 = 9.6分
9.6分 = 9.6 ÷ 60小时 = 0.16小时 12小时9分36秒 = 12.16小时
师生总结得出:由度化分,由分化秒,只要乘以60即可;由秒化分,由分化l度,只要除以60就行.
例1:计算:
(1)32°21'+68°48';
(2)90°-25°32';
(3)15°23'8”×4.
【答案】
(1)101°9’ (2)64°28’ (3)61°32'32”
【解析】
(1)32°21'+ 68°48'= 100°69’=101°9’
(2)90°- 25°32'= 89°60’- 25°32'= 64°28’
(3)15°23'8”×4 = 60°92'32”= 61°32'32”
练习:计算:
(1)13°29'+78°37',
(2)62°5'-21°39',
(3)107°43'÷5
【答案】
(1)92°6′ (2)40°26′ (3)21°32′36″
【解析】
(1)13°29′+78°37′ = 91°66′= 92°6′
(2)62°5′-21°39′=61°65′-21°39′= 40°26′
(3)107°43′÷5 = 21.4°8.6′=21°32.6′= 21°32′36″
3、平角、周角的度数:
例2:把一个周角8等分,每一份是多少度的角?
每一份角的度数:360°÷ 8 = 45°
(五)角的大小比较
如图已知∠ABC和∠DEF。
请大家讨论一下,用什么方法可以比较这两个角的大小?
分组讨论角的比较方法.在学生讨论过程中,教师深入学生中间巡视,观察并听取他们解决问题的方法和建议.可适当组织交流或分组汇报.师生共同归纳角的比较方法:
(1)度量方法: 用量角器量出角的度数 ,然后比较它们的大小。
(2)叠合方法: 把两个角叠合在一起 比较大小。
2、观察下列图形,图中共有几个角?它们之间有什关系?
3个,∠COB、∠COA、∠BOA;∠COA = ∠COB + ∠BOA
(六)角的平分线问题
问题1:用一副三角尺,你能画出哪些度数的角?
30°、45°、60°、90°;15°、75°、105°、120°、135°、150°。
问题2:在一张纸上画出一个角并剪下,将这个角对折,使其两边重合.想想看,折痕与角两边所成的两个角的大小有什么关系?
相等。折痕与角两边重合,相当于把角平均分成两份,所以两角相等。
由问题2的探讨,引出角的平分线定义及其几何表达式.类似的还有角的三等分线、四等分线等等.想一想,还有什么方法可画出一个角的平分线呢?
一般地,从一个角的顶点出发,把这个角分成两个相等的角的射线,叫做这个角的平分线。
可用量角器平分、尺规作图等方法。
(七)尺规作图
1、画一个角等于已知角,除用量角器外,你还有别的办法吗?
尺规作图法。
2、教师不用量角器和三角尺,而用直尺和圆规来画一个角等于已知∠AOB.
分组讨论:角的顶点和角的一边如何确定?角的另一边怎样画出?画图的关键是什么?
角的顶点和角的一边直接作出即可;角的另一边需要用尺规作图法确定;画图的关键是确定角的另一边上的一个点。
3、教师按课本的步骤边讲边画,学生跟着老师的步骤画.
① 以O点为圆心,适当长为半径作弧,分别交于OA,OB于点C,D;
② 做一条射线O′A′,以点O′为圆心,OC长为半径作弧,交O′A′于点C′;
③ 以点C′为圆心,CD长为半径作弧,交前弧于点D′;
④ 过点O′,D′做射线O′B′;
∠A′O′B′就是所求作的角。
4、已知∠1和∠2如下图所示,用尺规作图画出∠AOB=∠1+∠2,保留作图痕迹
(八)角的计算
例3:已知在平面内,∠AOB=70°,∠BOC=40°,求∠AOC的度数.
【答案】30° 或110°
【解析】
试题分析:∠BOC 可能在∠AOB里边,也可能在∠AOB外边,分情况计算即可。
解:∠BOC在∠AOB里边时,∠AOC = ∠AOB - ∠BOC = 70°- 40° = 30°
∠BOC在∠AOB外边时,∠AOC = ∠AOB + ∠BOC = 70° + 40° = 110°
故答案为30° 或110°。
例4:如图,∠AOB=35°,
∠BOC=90°,
OD是∠AOC 的平分线,
求∠BOD的度数.
三、课堂小结:
这节课你学习了哪些知识?
下课了,谢谢观看
主讲教师:数学老师
2021/小升初数学/总复习/专题复习/教学课件
谢谢观赏
21世纪教育网(www.21cnjy.com)中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
同课章节目录
