2021小升初数学总复习数与代数专题课件(191张PPT)
文档属性
| 名称 | 2021小升初数学总复习数与代数专题课件(191张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 4.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-27 22:18:52 | ||
图片预览








文档简介
数与代数专题
主讲教师:数学老师
2021/小升初数学/总复习/专题复习/教学课件
考点梳理
Knowledge network
01
考点解析
Question type analysis
02
课时训练
Real exercise
03
知识小结
Knowledge summary
04
CONTENTS
目录
数与代数 第1课时
1.进一步理解整数、分数、小数等的概念,沟通知识之间的联系和区别。
2.深入掌握在直线上表示数,学会简单的识图能力。
3.通过自主探索和合作学习,使学生在整理复习中形成完整的知识体系,掌握复习方法,提高综合运用能力。
【重点】对各种数的意义的理解。
【难点】掌握整理知识的方法,学会系统地看待知识的结构。
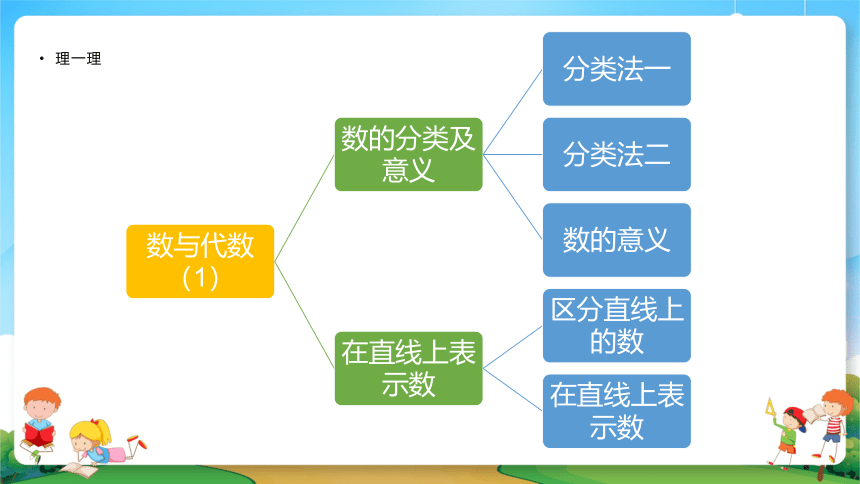
理一理
读一读,想一想
第30届夏季奥林匹克运动会于2012年7月27日至8月12日在英国伦敦举行。
你学过哪些数?它们在生活中有哪些应用?阅读下面的资料,你能
发现什么?
读一读,想一想
此次奥运会,来自205个国家和地区的代表队的总计10500名运员参加了26个大项(合302个小项)的比赛。花费4.96亿英镑修建的主体育场“伦敦碗”可容纳8万观众。
中国代表团共有396名运动员(男171名,女225名)参加比赛,约占总运员人数的3.77%。中国获得了38枚金牌、27枚银牌和23枚铜牌,列金牌榜和奖牌榜的第二位,其中金牌数约占总数302枚的八分之一,虽然金牌数比在北京举行的第29届奥运会出现了25.5%的负增长,但仍然取得了中国体育代表团参加在境外举办的历届奥运会的最好成绩。
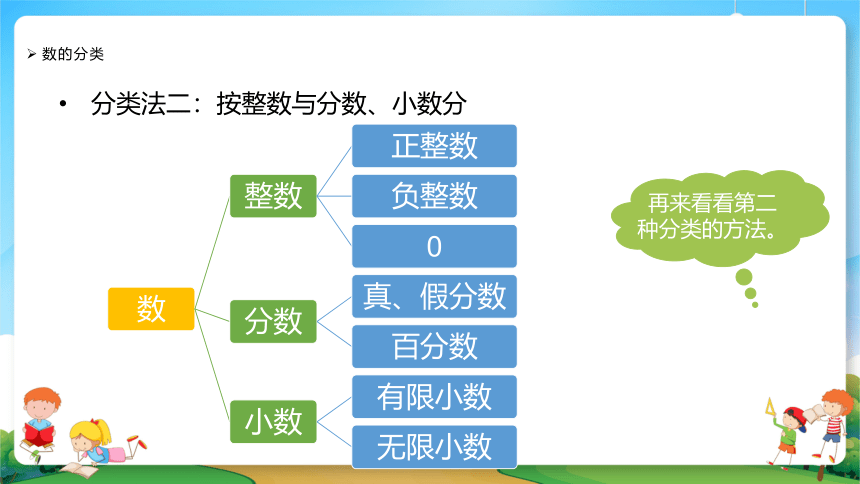
整数
小数
分数
百分数
负数
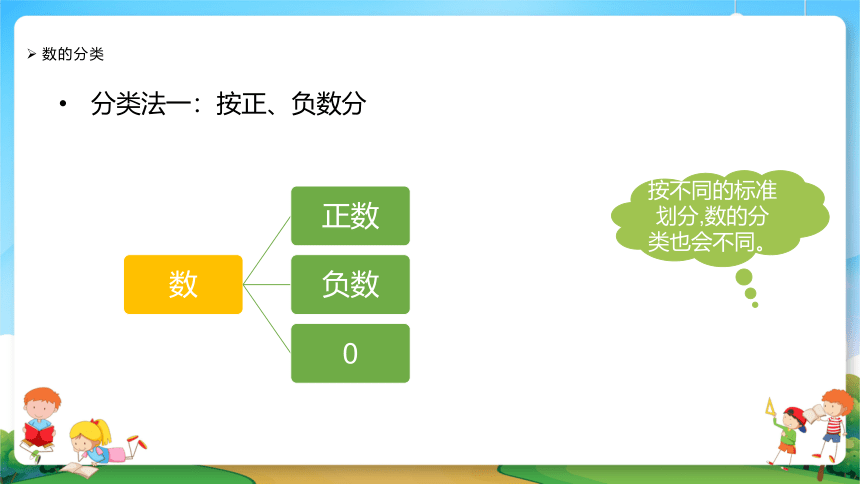
数的分类
按不同的标准划分,数的分类也会不同。
分类法一:按正、负数分
数的分类
再来看看第二种分类的方法。
分类法二:按整数与分数、小数分
数的分类
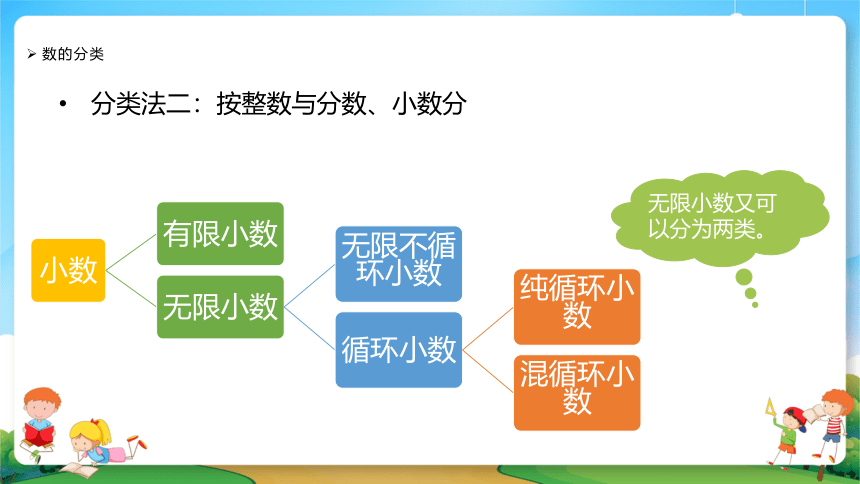
无限小数又可以分为两类。
分类法二:按整数与分数、小数分
数的意义
数的意义
数的意义
分数和百分数的关系:
分数既可以表示一个数,也可以表示两个数的比;而百分数只表示一个数占另一个数的百分比,不能用来表示具体的数。分数后面可以带单位名称,而百分数后面不能带单位名称。
小数:
像0.1、0.2、3.14、10.007……这样用来表示十分之几、百
分之几、千分之几……的数叫做小数。
在直线上表示数
-4 -3 -2 -1 0 1 2 3 4
( )是正数,( )是负数,
( )是自然数,( )是整数。
1,2,3,4
-1,-2,-3,-4
0,1,2,3,4
0,1,2,3,4,-1,-2,-3,-4
-1.5
1.5
( )
( )
在直线上表示数
-4 -3 -2 -1 0 1 2 3 4
3
-3.5
3, ,-3.5,-4。
14
?
-4
14
?
1
你能结合实际说明0.5、 、50%的含义吗?
12
?
0.5表示5个十分之一是多少。
12表示把单位1平均分成2份,其中的1份是多少。
50%表示一个数是另一个数的百分之五十。
?
小数通常表示具体的数量,
如1支铅笔0.5元……
(1)2008年8月3日,我国气象部门在新疆吐鲁番盆地的艾丁湖观测到了我国极端最高气温是49.7℃,可记作 ℃。1969年2月13日,我国气象部门在黑龙江漠河观测到了我国极端最低气温是零下52.3℃,可记作 ℃。
+49.7(或49.7)
-52.3
(2)如果a ÷b=c(a、b、c均为正数,且b≠0),那么a和b的最大公因数是 ,最小公倍数是 。
b
a
(3)一种商品打七折销售,“七折”表示原价的( )%。如果这种商品原价是100元,付款时要少付( )元。
70
30
2
说出下面各数中“2”表示的含义。
23
0.52
23
203.7
?
表示2个十
表示2个百分之一
表示2个三分之一
表示2个百
3
判断
(1)一头野牛重 吨,可以写成25%吨。( )
×
(2)小雨说大于2而小于6的数只有3,4,5。( )
×
4
填空,使每横行的各数相等。
小数
分数
百分数
0.4
80%
40%
0.75
75%
0.8
25
?
45
?
34
?
5
当a为哪些整数时,可以得到下面的答案
(1)在a3中,当a为( )时,a3可以表示自然数的单位。
?
3
(2)在a3中,当a为( )时,a3可以表示真分数。
?
1,2
(3)在a3中,当a为( )时, a3可以表示假分数。
?
大于或等于3的整数
6
数与代数 第2课时
1.进一步掌握十进制计数法,理解数位与计数单位的区别。
2.牢记数位顺序表,利用数位顺序表读数写数,比较数的大小。
3.复习整理因数、倍数的含义,解决因数、倍数在实际问题中的应用。
4.深入理解小数点的移动引起小数大小变化,从而培养学生整理知识的能力。
【重点】牢固掌握数位顺序表。
【难点】理解、掌握小数点的移动引起小数大小的变化。
理一理
计数单位和数位
数位顺序表
整数部分
小
数
点
小数部分
…
( )级
( )级
( )级
数
位
…
位
位
位
位
位
位
位
位
千
位
百
位
十
位
个
位
·
十
分
位
位
位
…
计
数
单
位
…
十
一
(个)
十
分
之
一
…
个
万
亿
万
十
万
百
万
千
万
亿
十
亿
百
亿
千
亿
百
千
万
十
万
百
万
千
万
亿
十
亿
百
亿
千
亿
百
分
千
分
百
分
之
一
千
分
之
一
数的读写、改写
整数的读法、写法
数的读写、改写
分数的读法、写法
读法
整数部分按照整数的读法来读,读完后加上个“又”字;分数部分先读分母,加上“分之”,后面再读分子。
读法
整数部分按照整数的写法来写,“又”字不用写,分数部分先读的是分母,写在下面,后读的是分子,写在上面,中间用分数线隔开。
数的读写、改写
百分数的读法、写法
数的读写、改写
小数的读法、写法
数的读写、改写
大数的改写方法
把多位数改写成用“万”或“亿”作单位的数,在万位或亿位的后面点上小数点,省略小数部分末尾的0,并在后面写上“万”或“亿”字,中间用“=”连接。
省略尾数改写成近似数
用“四舍五入”法省略万位或亿位后面的尾数,并在这个数的后面写“万”或“亿”字,中间用“≈”连接。
小数的近似数
要求把小数保留到哪一位,就把哪一位后面的数用“四舍五入”法省略,中间用“≈”连接。省略尾数改写成近似数。
假分数与带分数、整数之间的互化
假分数化成整数或带分数
例:把123和85改写成整数或带分数。
12÷3=4 123=4
85=135
?
假分数与带分数、整数之间的互化
整数化成假分数
用指定的分母作分母,用整数乘分母的积作分子。
带分数化成假分数
用整数部分乘分母的积加上分数部分的分子作分子,原分母不变。
例:5=5×44=204
623=6×3+23=203
?
数的大小比较
倍数、因数
想想什么是公倍数和公因数呢?
1
判断对错,对的画“√”,错的画“×”。
(1)把0.56扩大到它的100倍是560。 ( )
(2)0是正数。 ( )
(3)假分数的倒数一定都是真分数。 ( )
(4)所有的偶数都是合数。 ( )
(5)a(a>1)的所有因数都小于a。 ( )
×
×
×
×
×
解答问题
(1)写出15,48的因数。
(2)24和36的公因数都有哪些?
15的因数有:1,3,5,15。
48的因数有:1,2,3,4,6,8,12,16,24,48。
24和36的公因数有:1,2,3,4,6,12。
2
一箱苹果有40多个,如果把这箱苹果每8个装一盒,还剩余6个;如果每10个装一盒,也剩余6个。这箱苹果有多少个?
5×8+6=46
10×4+6=46
答:这箱苹果有46个。
3
用 2 、7、4 、5 和5个0写出符合下列要求的数。
最大的九位数:
百万位上是七的最小九位数:
只读出一个零的最小九位数:
个级数位上都是零最小九位数:
754200000
207000045
200000457
204570000
4
第一位是5的最小的倍数,第二位缩小为原来的1100是0.02,第三位是8的最大的因数,第四位是最大的一位自然数,第五位是最小的自然数,第六位是10以内最大的奇数。猜猜这个密码是多少。
?
528909
5
数与代数 第3课时
【重点】能够正确、灵活进行四则混合运算。
【难点】深入掌握四则运算各部分名称之间的关系。
1.进一步理解四则运算的意义,分析在四则运算中0或1参与运算时的特殊情况。
2.深入理解整数、分数、小数四则运算的异同点。帮助学生在辨析学
会整合、理解知识。
3.根据学过的知识整理四则运算中各部分名称之间的关系,利用各部分
名称之间的关系解决实际问题。
理一理
四则运算的运算意义
+
加法
把两个数合成一个数的运算
-
减法
已知两个数的和与其中的一个加数,求另一个加数的运算。
×
乘法
求几个相同加数的和的简便运算。
÷
除法
已知两个乘数的积与其中一个乘数,求另一个乘数的运算。
不同类数(整数、小数、分数)的四则运算的异同
相同点
不同类数(整数、小数、分数)的四则运算的异同
不同点
不同类数(整数、小数、分数)的四则运算的异同
例:计算下面各题。
1260+60=
5700-268=
22.8+1.24=
12+13=
?
450÷3=
15.6×4÷0.2=
1320
5432
24.04
150
312
56
?
0或1参与运算的特殊情况
例: 0+8=0,9-0=9
7×0=0,0÷8=0
0或1参与运算的特殊情况
例:
1×10=10,1÷8=18
?
四则运算各部分之间的关系
26+32=58
58-26=32
58-32=26
2.5×4=10
10÷2.5=4
10÷4=2.5
减法是加法的逆运算
乘法是加法的简便运算
除法是乘法的逆运算
a+a+a+……+a
n个
=a×n
四则运算各部分之间的关系
加数+加数=和
被减数-减数=差
一个加数=和-另一个加数
被减数=减数+差
减数=被减数-差
乘数×乘数=积
被除数÷除数=商
一个乘数=积÷另一个乘数
被除数=商×除数
除数=被除数÷商
四则运算各部分之间的关系
例:根据乘法算式,写出两道除法算式和一道乘法算式。根据加法算式写出两道减法算式和一道加法算式。
26+32=58
125×8=1000
32+26=58
58-26=32
58-32=26
8×125=1000
1000÷8=125
1000÷125=8
四则运算各部分之间的关系
例:根据乘法算式,写出两道除法算式和一道乘法算式。根据加法算式写出两道减法算式和一道加法算式。
1.6+2.7=4.3
2.5×4=10
2.7+1.6=4.3
4.3-2.7=1.6
4.3-1.6=2.7
4×2.5=10
10÷2.5=4
10÷4=2.5
四则运算的顺序
四则运算的顺序
计算,并说说运算顺序。
(128-75)×2
=53×2
=106
45+28÷4
=45+7
=52
47+36+18
=83+18
=101
12.5×8÷10
=100÷10
=10
27+68=
910-540=
95
370
18×40=
720
910÷70=
78-0.8=
13
77.2
3÷12=
6.3÷0.1=
63
36×25%=
9
3
94+34=
?
14
?
口算
1
3?25=
?
56×35=
?
12÷14=
?
3.48+6.52=
1.02-0.43=
10
0.59
0.25×0.8=
0.2
12.6÷3=
4.2
235
?
12
?
2
?
口算
1
(3)0除以任何数都得0。( )
判断对错
(1)做四则混合运算时,先算加减后算乘除。( )
(2)被减数等于减数加差。( )
×
√
×
2
计算
5×47+5×53
=5×(47+53)
=500
(40-13.5)÷14
?
=26.5×4
=106
40÷(15-7)
=40÷8
=5
12.5×(240-480×16)
?
=12.5×(240-80)
=2000
3
数与代数 第4课时
1.复习学过的五种运算定律:加法交换律、加法结合律、乘法交换律、乘法结合律、乘法分配律。
2.灵活运用五种定律在四则混合运算中解决问题。
3.掌握估算的运用原则,了解估算策略,为解决实际问题打好基础。
【重点】牢固掌握运算定律帮助计算。
【难点】运用原有知识解决实际问题。
理一理
运算律
看算式归纳表格
15+28=28+15
65+75+25=65+(75+25)
23×4=4×23
78×125×8=78×(125×8)
8×(125+2)=8×125+8×2
运算律
名称
举例
用字母表示
加法交换律
15+28=28+15
a+b=b+a
加法结合律
乘法交换律
乘法结合律
乘法分配律
65+75+25
=65+(75+25)
a+b+c=a+(b+c)
23×4=4×23
a×b=b×a
78×125×8
=78×(125×8)
a×b×c=a×(b×c)
8×(125+2)
=8×125+8×2
a×(b+c)=a×b+a×c
看算式归纳表格
运算性质
运算性质
例:78.4-12.38-24.62 104÷58÷3215
?
=104÷(58×3215)
?
=78.4-(12.38+24.62)
=78.4-37
=41.4
=104÷43
?
=26
估算策略
估算策略
估算应用
例:完成下面的问题。
(1)7.99×9.99与80比,哪个大?
(2) 12+35比1大吗?
?
(3)妈妈带100元去书店买书,她买了两本文学书,每本20.6元;又花39.6
元买了一本汉语词典;之后,妈妈还想买一本家庭菜谱,有两本菜谱可供选择:薄本的13.7元,厚本的23.8元。请帮妈妈估算一下,这时她的钱够买哪一本?
估算应用
(1)7.99×9.99与80比,哪个大?
把7.99估计成8,把9.99估计成10,8×10=80,但是因为我们利用的是四舍五入法,也就是比五大的就进1,实际上比8和10小,所以结果比80小。
(2) 12+35比1大吗?
?
35比12大,所以看成是两个12相加,结果等于1,所以35比1大。
?
估算应用
(3)妈妈带100元去书店买书,她买了两本文学书,每本20.6元;又花39.6
元买了一本汉语词典;之后,妈妈还想买一本家庭菜谱,有两本菜谱可供选择:薄本的13.7元,厚本的23.8元。请帮妈妈估算一下,这时她的钱够买哪一本?
两本文学书每本估计是21元,两本是42元词典估计是40元,还剩18元,所以只够买薄本的13.7元的菜谱。
1
填一填
(1)27除以6的商是4,余数是3,如果被除数和除数都扩大到原
来的100倍,商是( ),余数是( )。
4
(2)如果a÷b=15……6,那么a最小是( )。
(3)在一个减法算式,差是18,如果被减数不变,减数增加3.2,差( )。
300
111
14.8
457+786+214
=457+(786+214)
=1457
125×16
=125×8×2
=2000
14×59+14×49
?
45?27×59
?
=14×(59+49)
?
=14
?
= 45×59?27?×59
?
=10
?
2
计算下面各题
32+35+25
?
125×24
=125×(8×3)
=125×8×3
=1000×3
=3000
=32+(35+25)
?
=32+1
?
=52
?
2
计算下面各题
六年级有5个班,1至5班的人数依次为:43、 40、41、44、42,学校小礼堂有200个座位,如果召开六年级毕业典礼,需要加椅子吗?
人数最少的班有40人,5个班总人数一定大于200人,需要加椅子。
3
803-207≈
798+205≈
600
1000
23×498≈
10000
632÷69≈
9
4
估算
估一估,在 里填上“>”或“<”
8+75
?
712×397
?
3.7?56
?
59×9.9
60
>
<
32
32÷1.2
57×0.8
57
370
10.1×37
9
2.7
3
49÷1019
?
1
<
>
>
>
>
<
5
0.65×101
=0.65×(100+1)
=0.65×100+0.65×1
=65+0.65
=65.65
0.4×37+0.6×37
?
=(0.4+0.6)×37
?
=1×37
?
=37
?
6
计算
12+13÷25?23
?
23÷89×1?34
?
=56÷25?23
?
=23÷89×14
?
=2512?23
?
=34×14
?
=316
?
=1712
?
6
计算
33338712×79+790×6666114
?
=333387.5×79+790×66661.25
=33338.75×10×79+790×66661.25
=33338.75×790+790×66661.25
=(33338.75+66661.25)×790
=100000×790
=79000000
7
巧算
数与代数 第5课时
1.归纳、总结解决实际问题的主要步骤,从中感受数学的实用性。
2.运用解决实际问题的主要步骤解决实际问题,初步建立学生的社会实践性。
【重点】归纳解决实际问题的主要步骤。
【难点】运用解决问题的主要步骤解决实际问题。
理一理
解决问题归类
相遇
问题
路程÷(甲速+乙速)=相遇时间
(甲速+乙速)×相遇时间=路程
追击
问题
(假设甲速大于乙速)
甲与乙的距离÷(甲速-乙速)=追上时间
(甲速-乙速)×追上时间=甲与乙的距离
工程
问题
工作总量÷工作效率=工作时间
工作总量÷工作时间=工作效率
工作效率×工作时间=工作总量
解决问题归类
和差问题
(和+差)÷2=大数
大数-差=小数
(和-差)÷2=小数
小数+差=大数
和-小数=大数
鸡兔同笼问题
假设全是鸡
(总腿数-总头数×2)÷(4-2)=兔的只数;
假设全是兔
(总头数×4-总腿数)÷(4-2)=鸡的只数。
解决问题归类
求一个数是另一个数的几分之几(或百分之几)。
比较量÷标准量(单位“1”)=分率(百分率)
求一个数的几分之几(或百分之几)是多少。
单位“1”的量× 对应的分率(百分率)=要求的量
求比一个数多(少)几分之几(或百分之几)的数是多少。
标准量× (1 ± 分率或百分率)=比较量(要求的量)
分数/百分数问题
解决问题归类
已知一个数的几分之几(或百分之几)是多少,求这个数。
求一个数比另一个数多(少)几分之几(或百分之几)。
多的量(少的量)÷单位“1”=分率(百分率)
已知一个数比另一个数多或少几分之几或百分之几,求这个数。
已知量÷分率(百分率)=要求的量(单位“1”)
已知量÷分率(百分率)=要求的量(单位“1”)
例:
六年级举行“小发明”比赛,六(1)班同学上交32件作品,六(2)班比六(1)班多交14,两个班共交了多少件作品?
?
六(1)班:
六(2)班:
32件
?件
比六(1)班多
4
1
可以画线段图分析。
例:
六年级举行“小发明”比赛,六(1)班同学上交32件作品,六(2)班比六(1)班多交14,两个班共交了多少件作品?
?
32×1+14=
?
32+40=
?
答:两个班共交了72件作品。
40(件)
72(件)
解决问题的步骤
1
书店第一季度的营业额为15万元,第二季度的营业额为16.5万元。第二季度的营业额比第一季度增长了百分之多少?
16.5-15=1.5(万元)
1.5÷15×100%=10%
答:第二季度的营业额比第一季度增长了10%。
A城开往B城的火车平均每小时行120千米,4小时可以到达;提速
后,平均每小时比原来多行40千米,几小时到达?
120×4=480(千米)
120+40=160(千米)
答:3小时到达。
480÷160=3(小时)
先求路程,再求提速后的速度,最后求时间。
2
女生有150人,男生是女生的 ,男生、女生一共有多少人?
150×45=
?
150+120=
?
270(人)
?
答:男生、女生一共有270人。
120(人)
3
一个旅游公司,去年接待游客24000人,今年比去年减少10%,今年接待游客多少人?
24000×(1-10%)=21600(人)
答:今年接待游客21600人。
4
河东区要修一条640米的景观大道,第一周修了这条路的14,第二周修了这条路的20%,还剩多少米没修?
?
640×(1-14- 20%)
?
=640×0.55
=352(米)
答:还剩352米没修。
先求剩下的占这条路的几分之几,再求剩下多少米没修。
5
学生夏令营组织远足,原计划3小时走完11.25 km。实际2.5小时就走完了原定路程。实际比原计划每小时多走多少千米?
11.25÷2.5-11.25÷3
=4.5-3.75
=0.75(km)
答:实际比原计划每小时多走0.75 km。
6
下表中是G35次列车途径站点的相关信息。你能估算一下这趟列
车在行驶全程中(扣除停留时间)的平均速度大约是多少吗?
7
17:24-11:06-17分≈6(时)
1487÷6≈250(km/h)
答:平均速度大约是250km/h。
7
下表中是G35次列车途径站点的相关信息。你能估算一下这趟列
车在行驶全程中(扣除停留时间)的平均速度大约是多少吗?
1.8+0.6+半臂长>2.6
答:爸爸能换成灯泡。
8
小红家客厅的顶灯需要更换一个灯泡。已知灯泡距地面2.6m,爸爸身高1.80m,小红搬了一个高0.6m的凳子。爸爸能换成灯泡吗?
数与代数 第6课时
1.整理复习用字母表示数、数量关系、计算公式及运算定律,提升学生的自主归纳、整理的能力。
2.理解等式与方程的联系与区别,使学生深刻理解方程的意义,理清解方程的一般步骤,灵活地掌握解方程的方法。
3.在实际问题中掌握列方程解应用题的一般步骤,使学生掌握用方程解决问题,提高学生解决问题的综合实践能力。
【重点】掌握用字母表示数、运算定律及计算公式,灵活解方程。
【难点】利用列方程解应用题的一般步骤解决数学问题。
理一理
用字母表示数
字母表示数量关系
路程=速度×时间
s=vt
总价=单价×数量
c=an
工作总量=工作效率×工作时间
c=at
字母表示计算方法
ba+ca=b+ca
?
用字母表示数
用字母表示运算定律
{5940675A-B579-460E-94D1-54222C63F5DA}名称
用字母表示
加法交换律
加法结合律
乘法交换律
乘法结合律
乘法分配律
a+b=b+a
(a+b)+c=a+(b+c)
a×b=b×a
(a×b)×c=a×(b×c)
(a+b)×c=a×c+b×c
用字母表示数
注意事项
方程
方程
等式的性质
等式的两边同时加上(或减去)同一个数,等式仍然成立;等式的两边同时乘(或除以)同一个数(0除外),等式仍然成立。
例:解方程,说一说什么是解方程,什么是方程的解。
2x+4=20
?
解:
2x=20?4
?
2x=16
?
x=16÷2
?
x=8
?
列方程解应用题
用方程解决问题的步骤
列方程解应用题
列方程解决实际问题的类型
1
小雨今年a岁,比妈妈小23岁,2年后小雨和妈妈的年龄和是多少?
2年后小雨年龄:(a+2)岁
2年后妈妈年龄:(a+23+2)岁
2年后年龄和是:(a+2)+(a+23+2)=(2a+27)岁
写出平行四边形、长方形、正方形、三角形、梯形的面积公式,长方形、正方形的周长公式。
平行四边形面积=底×高,S=ah
长方形面积=长×宽,S=ab
正方形面积=边长×边长,S=a·a=a2
三角形面积=底×高÷2,S=ah÷2
梯形面积=(上底+下底)×高÷2,S=(a+b)h÷2
长方形周长=(长+宽)×2,C=2(a+b)
正方形周长=边长×4,C=4a
2
(1)李奶奶家本月用电a千瓦时,比上个月多用10千瓦时,上个月用电
( )千瓦时。如果每千瓦时电的价格是c元,李奶奶家本月的电费是( )元。李奶奶家银行缴费卡上原有215元,扣除本月电费后,还剩( )元。
(3)小明今年m 岁,妈妈的岁数比她的3倍少6岁。妈妈的岁数是( )岁。如果m=12,妈妈今年是( )岁。
(4)三个连续的自然数,最大的一个是n,那么最小的一个数是( )。
a-10
ac
215-ac
3m-6
30
n-2
填空
3
学校买来9个足球,每个a元,又买来b个篮球,每个58元。
9a表示 ;
58b表示 ;?
58-a表示 ;?
9a+58b表示 ;?
如果a=45,b=6,则9a+58b= 。
9个足球的钱数
b个篮球的钱数
每个篮球比足球贵的钱数
买9个足球和b个篮球共用的钱数
753
4
判断题
(1)所有的等式都是方程,所有的方程不一定都是等式。( )
?
(2)3+4=7是等式,不是方程。 ( )
√
(3)方程的解可以是整数、小数、分数、百分数。( )
√
5
x=13+0.25
?
4+0.7x=102
?
解:
解:
x=712
?
x?0.25=13
?
0.7x=102?4
?
0.7x=98
?
x=98÷0.7
?
x=140
?
解方程
6
x4=30%
?
23x+12x=42
?
解:
解:
x=30%×4
?
x=1.2
?
76x=42
?
x=42÷76
?
x=36
?
解方程
6
绿化队为一个居民社区栽花。栽月季花240棵,再加上16棵就是所栽丁香花棵树的2倍。栽了多少棵丁香花?
7
解:设栽丁香花x棵。
2x=240+16
x=128
答:栽了128棵丁香花。
绿化队为一个居民社区栽花。栽月季花240棵,再加上16棵就是所栽丁香花棵树的2倍。栽了多少棵丁香花?
7
商店卖一种书包,如果每个售价为150元,那么售价的60%是进价,售价的40%就是赚的钱。现在要搞促销活动,为保证一个书包赚的钱不少于30元,应该怎样确定折扣?
答:八折或八折以上。
150×60%=90(元)
90+30=120(元)
120÷150=80%
8
数与代数 第7课时
1.通过比较比和比例各部分名称和基本性质,深刻理解比和比例的意
义,联系及区别。
2.通过回顾正比例关系、反比例关系的概念,使学生正确掌握在生活
事例中对于正比例和反比例的判断方法,在实际问题中能够灵活运用
正比例和反比例解决问题。
【重点】掌握比和比例的意义和性质。
【难点】掌握在生活事例中对于正比例和反比例的判断方法。
理一理
比和比例的联系与区别
{5940675A-B579-460E-94D1-54222C63F5DA}
比
比例
意义
各部分名称
基本性质
两数相除又叫两个数的比。
两个比相等的式子叫作比例。
0.6 :0.8 = 0.75
前项
后项
比值
…
…
…
2 : 3 = 6 : 9
内项
外项
比的前项和后项都乘或除以相同的数(0除外)比值不变。
在比例里,两外项之积等于两内项之积。
化简比的依据
解比例的依据
化简比、求比值
化简比的方法
整数比
小数比
分数比
比的前项和后项同时除以它们的最大公因数。
把比前、后项的小数点向右移动相同的位数,转化成整数比再化简。
把比前、后项同时乘分母的最小公倍数,转化成整数比再化简。
化简比、求比值
{616DA210-FB5B-4158-B5E0-FEB733F419BA}
一般方法
结果
求比值
化简比
根据比值的意义,用前项除
以后项。
结果是一个数,可以是整数、小数或分数。
根据比的基本性质,把比的前项和后项都乘或者除以相同的数(零除外)。
结果是一个比,而且是最简整数比。
求比值和化简比的区别
比、分数、除法之间的联系及区别
{8799B23B-EC83-4686-B30A-512413B5E67A}
比
除法
分数
联 系
区 别
前项
后项
比号
比值
被除数
除号
除数
商
分子
分数线
分母
分数值
比是两个数之间的倍数关系
除法是一种运算
分数是一种数
比、分数、除法之间的联系及区别
比的基本性质、分数的基本性质、商不变的性质三者之间联系及区别
比的基本性质
分数的基本性质
商不变的性质
比的前项和后项同时乘或除以相同的数(0除外),比值不变。
分数的分母和分子同时乘或除以相同的数(0除外),分数的大小不变。
在除法中,被除数和除数同时乘或除以相同的数(0除外),商不变。
商不变的性质、比的基本性质和分数的基本性质的内容实质上是一样的。
比和比例的应用
比例尺
{8799B23B-EC83-4686-B30A-512413B5E67A}
分 类
举 例
意 义
一幅图的图上距离和实际距离的比。
按表现形式,可以分为数值比例尺和线段比例尺。
按将实际距离放大还是缩小分,分为缩小比例尺和放大比例尺。
1:500000
0
50km
1:500000
20:1
比和比例的应用
解决按比分配问题的解题步骤
{5940675A-B579-460E-94D1-54222C63F5DA}名称
联系
区别
变化规律
关系式
图像
正比例
反比例
比和比例的应用
正比例和反比例
1.两种相关联的量。
2.一种量随着另一种量的变化而变化。
相对应的两个量的比值(商)一定。
相对应的两个量的积一定。
y:x=k
(一定)
xy=k
(一定)
1
(1)7÷8可以写成( )。
(2)( )叫方程。
含有未知数的等式
(3)2∶4=( )∶12。
6
(4)在比例里,两个内项的积是70,两个外项的积是( )。
70
填空
7:8或78
?
判断下面两种量是否成比例,成什么比例?
(1)爸爸上班的路程一定,速度和时间。
(2)故事书的总页数一定,看的页数和剩余的页数。
(3)单价一定,总价和数量。
(4)三角形的面积一定,三角形的底与底边上的高。
(1)成比例,成反比例
(2)不成比例
(3)成比例,成正比例
(4)成比例,成反比例
2
判断题
(1)甲数除以乙数的商是1.4,甲数和乙数的比是7∶5。 ( )
(2)π是圆的周长与直径的比值。 ( )
(3)甲、乙两人同时从A地到B地,甲6小时到达,乙5小时到达。甲、乙所用的时间的比和速度的比都是6∶5。 ( )
(4)在比例中,两个外项的积除以两个内项的积,商是0。 ( )
(5)因为3×10=5×6,所以3:5=10:6。 ( )
(6) 18:30和3:5可以组成比例。 ( )
√
×
√
×
×
√
3
伦敦奥运会一块金牌的黄金含量与金牌总重的比为6:412。一块金牌总重412 g,302块金牌需要黄金多少克?
答:302块金牌需要黄金1812克。
412×6412=
?
6×302=
?
6(克)
1812(克)
4
北京到济南高速公路距离大约为430 km,北京到天津大约为120 km。一辆汽车从北京出发开往济南,当行驶到天津时用了1.5小时。按照这个速度,北京到济南全程需要多少小时?
答:北京到济南全程需要5.375小时。
解:设需要x小时。
430x=1201.5
?
x=5.375
?
5
同一幅地图上,量得甲、乙两地的直线距离是20cm,甲、丙两地的直线距离是12 cm。如果甲、乙两地的实际距离是1600 km,那么甲、丙两地的实际距离是多少?
答:甲、丙两地的实际距离是960 km。
解:设甲、丙两地的实际距离为x km。
201600=12x
?
x=960
?
6
六年级(2)班乘车去农家果园采摘草莓,汽车以40千米/时的速度行驶1小时到达果园,在果园活动了2小时,然后乘车以相同的速度返回。观察下面两幅图象,它们有什么不同?
返回时汽车行驶的路程不断增加,而离校距离越来越近(少),与来时的方向相反。
7
数与代数 第8课时
1.复习利用数形结合寻找规律解决实际问题的方法。
2.进一步巩固、发展学生找规律的能力,体会找规律对解决问题的重要性及数形结合数学思想的重要性。
3. 激发学生学习数学、探索规律的兴趣。提高学生的合作意识。
【重点】复习利用数形结合寻找规律解决问题的方法。
【难点】能够正确的利用数形结合法分析归纳出规律。
忆一忆
回忆我们学过的知识,想想解决这类问题用什么方法?
……
如下图,摆1个正方形需用4根小棍,摆2个正方形需用7根小棍,摆
3个正方形需用10根小棍,照这样摆下去,第n个图形需用多少根小
棍?
找规律。
第n个图形需用4+3(n-1)根小棍
找规律
例:每两个点连成一条线段,一共可以连成多少条线段呢?
有什么规律呢?
{5DA37D80-6434-44D0-A028-1B22A696006F}点数
增加条数
总条数
A
B
A
B
1
我们通过画图来看看!
{5DA37D80-6434-44D0-A028-1B22A696006F}点数
增加条数
总条数
1
A
B
C
A
B
A
B
C
2
3
{5DA37D80-6434-44D0-A028-1B22A696006F}点数
增加条数
2
总条数
1
3
A
B
C
A
B
C
D
A
B
C
D
A
B
3
6
A
B
C
D
E
{5DA37D80-6434-44D0-A028-1B22A696006F}点数
增加
条数
2
3
总条数
1
3
6
A
B
C
D
A
B
C
A
B
C
D
E
A
B
4
10
3个点共连:1+2=3(条)
4个点共连:1+2+3=6(条)
{5DA37D80-6434-44D0-A028-1B22A696006F}点数
2个点
3个点
4个点
5个点
6个点
增加
条数
2
3
4
总条数
1
3
6
10
5个点共连:1+2+3+4=10(条)
5
15
6个点共连:1+2+3+4+5=15(条)
你在你有什么发现吗?
{5DA37D80-6434-44D0-A028-1B22A696006F}点数
2个点
3个点
4个点
5个点
6个点
增加
条数
2
3
4
总条数
1
3
6
10
5
15
有几个点,增加的条数比点数少1。
计算有几条线段,就是从1+2+3+…一直加到比点数少1的
数再求和就可以了。
n个点
12个点共连
20个点共连
根据规律,你知道12个点、20个点能连成多少条线段?请写出算式。
1+2+3+4+5+6+7+8+9+10+11=66(条)
1+2+3+…+19=190(条)
1+2+3+…+(n-1)=n(n-1)÷2
和=(首项+末项)×项数÷2
这种算式叫做等差数列。
(1)
(2)
(3)
(4)
(1)第7幅图有多少个棋子?第15幅图呢?
1 4 9 16
观察下图,想一想。
7×7=49(个)
15×15=225(个)
答:第7幅图有49个棋子,第15幅图有225个棋子。
1
(1)
(2)
(3)
(4)
(2) 每边的棋子数与图形的序号有什么关系?
{5940675A-B579-460E-94D1-54222C63F5DA}
图形的序号
每边的棋子数
1
2
1
4
3
2
3
4
……
……
答:每边的棋子数与图形的序号相等。
1
{5940675A-B579-460E-94D1-54222C63F5DA}
(1)
(2)
(3)
(4)
图形的序号
每边的棋子数
1
2
1
4
3
2
3
4
……
……
(3)第n幅图每边有多少个棋子?一共有多少个棋子?
每行的棋子数×行数=棋子总数
n×n=棋子总数
n2=棋子总数
n
n
答:第n幅图每边有n个棋子,一共有n2个棋子。
1
摆一摆,找规律。
(1)第6个图形是什么图形?
答:第6个图形是平行四边形。
2
(2)摆第7个图形需要用多少根小棒?
答:需要用15根小棒。
摆一摆,找规律。
2
(3)摆第n个图形需要用多少根小棒?
答:需要用2n+1根小棒。
摆一摆,找规律。
2
(1)多边形的内角和与它的边数有什么关系?
答:多边形的内角和等于边数减2,再乘180°。
{5940675A-B579-460E-94D1-54222C63F5DA}多边形
……
边数
3
4
5
6
……
内角和
180°
360°
……
3
(2)一个九边形的内角和是多少度?
答:九边形的内角和是1260°。
{5940675A-B579-460E-94D1-54222C63F5DA}多边形
……
边数
3
4
5
6
……
内角和
180°
360°
……
3
(3)一个n边形的内角和是多少度?
答:n边形的内角和是180°×(n-2)。
{5940675A-B579-460E-94D1-54222C63F5DA}多边形
……
边数
3
4
5
6
……
内角和
180°
360°
……
3
数与代数 第9课时
1.复习通过列表格推理从而解决实际问题的方法。
2.进一步发展逻辑推理能力和解决问题的能力,体会列表法对解决问题的重要性。
3. 激发学生学习数学、解决数学问题的兴趣。提高学生的合作意识。
【重点】熟练掌握列表法解决实际问题的方法。
【难点】列出表格后能够正确的进行逻辑推理并解决问题。
忆一忆
学校秋季运动会乒乓球比赛项目中有甲、乙、丙、丁四位同学参加,比赛规则要求四位选手彼此见面,总共需要进行多少场比赛?
回忆我们学过的知识,想想解决这类问题用什么方法?
可以用列表法。
总共需要进行6场比赛。
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
甲
乙
丙
丁
甲
√
√
√
乙
√
√
丙
√
丁
例:
六年级有三个班,每班有2个班长。开班长会时,每次每班只要一个班长参加。第一次到会的有A、B、C;第二次有B、D、E;第三次有A、E、F。请问:哪两位班长是同班的?
列表法解决问题
怎样才能有序思考呢?
例:
六年级有三个班,每班有2个班长。开班长会时,每次每班只要一个班长参加。第一次到会的有A、B、C;第二次有B、D、E;第三次有A、E、F。请问:哪两位班长是同班的?
{8799B23B-EC83-4686-B30A-512413B5E67A}
A
B
C
D
E
F
第一次
1
1
1
0
0
0
第二次
第三次
0
1
0
1
1
0
1
0
0
0
1
1
用数字“1”表示到会
用数字“0”表示没到会
{8799B23B-EC83-4686-B30A-512413B5E67A}??
A
B
C
D
E
F
第一次
第二次
第三次
1
1
0
0
0
1
1
1
0
0
0
1
0
0
1
1
1
0
提示:开班长会时,每次每班只要一个班长参加。
例:
六年级有三个班,每班有2个班长。开班长会时,每次每班只要一个班长参加。第一次到会的有A、B、C;第二次有B、D、E;第三次有A、E、F。请问:哪两位班长是同班的?
那一起参加班会的一定不在同一班级。有且只有一个班长参加。
例:
六年级有三个班,每班有2个班长。开班长会时,每次每班只要一个班长参加。第一次到会的有A、B、C;第二次有B、D、E;第三次有A、E、F。请问:哪两位班长是同班的?
{8799B23B-EC83-4686-B30A-512413B5E67A}??
A
B
C
D
E
F
第一次
第二次
第三次
1
1
0
0
0
1
1
1
0
0
0
1
0
0
1
1
1
0
1
√
√
√
√
√
0
1
√
A和谁可能是同班?
{8799B23B-EC83-4686-B30A-512413B5E67A}??
A
B
C
D
E
F
第一次
第二次
第三次
1
1
0
0
0
1
1
1
0
0
0
1
0
0
1
1
1
0
1
√
√
√
√
√
0
1
√
第一次:A只可能和D、E、
F同班。
第二次:A只可能和D、E同班。
第三次:A只可能和D同班。
例:
六年级有三个班,每班有2个班长。开班长会时,每次每班只要一个班长参加。第一次到会的有A、B、C;第二次有B、D、E;第三次有A、E、F。请问:哪两位班长是同班的?
例:
六年级有三个班,每班有2个班长。开班长会时,每次每班只要一个班长参加。第一次到会的有A、B、C;第二次有B、D、E;第三次有A、E、F。请问:哪两位班长是同班的?
{8799B23B-EC83-4686-B30A-512413B5E67A}??
A
B
C
D
E
F
第一次
第二次
第三次
1
1
0
0
0
1
1
1
0
0
0
1
0
0
1
1
1
0
1
√
√
√
1
B、C可能和谁是同班?
{8799B23B-EC83-4686-B30A-512413B5E67A}??
A
B
C
D
E
F
第一次
第二次
第三次
1
1
0
0
0
1
1
1
0
0
0
1
0
0
1
1
1
0
1
√
√
√
1
A和D同班,则B只可能和E、F同班,根据第二轮推测,B和F同班,据此可推出C、E同班。
例:
六年级有三个班,每班有2个班长。开班长会时,每次每班只要一个班长参加。第一次到会的有A、B、C;第二次有B、D、E;第三次有A、E、F。请问:哪两位班长是同班的?
请问:他们的职业各是什么?
王阿姨、刘阿姨、丁叔叔、李叔叔分别是工人、教师、军人。王阿姨是教师;丁叔叔不是工人;只有刘阿姨和李叔叔的职业相同。
王阿姨
刘阿姨
丁叔叔
李叔叔
工人
教师
军人
√
×
×
√
×
×
√
√
答:王阿姨是教师,丁叔叔是军人,刘阿姨和李叔叔都是工人。
1
学校组织了足球,航模和电脑兴趣小组,淘气、笑笑和小明分别参加了其中一项。笑笑不喜欢踢足球,小明没有参加电脑小组,淘气喜欢航模。他们分别在哪个小组。
足球
航模
电脑
淘气
笑笑
小明
×
×
×
×
×
×
√
√
√
答:淘气在航模小组, 笑笑在电脑小组,小明在足球小组。
2
球场休息时,保管员慌忙中把甲、乙、丙三个运动员先前交给他的水瓶都递送错了,结果甲喝的是丙的。乙、丙各喝的是谁的?
甲
乙
丙
甲的水
乙的水
丙的水
×
√
×
×
×
×
√
√
答:乙喝的是甲的,丙喝的是乙的。
×
3
下图中一共有几条线段?
或7×(7-1)÷2=21(条)
(7-1)+5+4+3+2+1=21(条 )
4
小明、小莉、小刚、小芳四个好朋友站成一排拍毕业纪念照,要求男女间隔排列,一共有多少种站法?
(5)小莉 小明 小芳 小刚
(6)小莉 小刚 小芳 小明
(7)小芳 小明 小莉 小刚
(8)小芳 小刚 小莉 小明
(1)小明 小莉 小刚 小芳
(2)小明 小芳 小刚 小莉
(3)小刚 小莉 小明 小芳
(4)小刚 小芳 小明 小莉
答:共有8种不同的站法。
5
方法一:用列举法
B1 B2
小明 小刚 小莉 小芳
A1 A2 B1 B2
第一位 第二位 第三位 第四位
A1 A2
答:共有8种不同的站法。
2×4=8
互换
互换
小明、小莉、小刚、小芳四个好朋友站成一排拍毕业纪念照,要求男女间隔排列,一共有多少种站法?
方法一:用字母表示法
5
警察抓住了4个偷东西的嫌疑人,其中的一个人是主谋。审问谁是主谋时,甲说:我不是主谋。乙说:丁是主谋。丙说:我不是主谋。
丁说:甲是主谋。已知他们4人中只有一个人说了真话。主谋是谁?
{93296810-A885-4BE3-A3E7-6D5BEEA58F35}
甲
乙
丙
丁
是否
真话
否
是
是
是
结论
主谋
非主谋
非主谋
主谋
是否
真话
是
否
否
否
结论
非主谋
非主谋
主谋
非主谋
通过列表,结合题目信息可知丙是主谋。
6
数与代数 第10课时
1.复习通过等量代换从而解决实际问题的方法,复习简单的几何证
明方法。
2.进一步发展逻辑推理能力和解决问题的能力,体会等量代换对解决
问题的重要性。
3. 激发学生学习数学、解决数学问题的兴趣。提高学生的合作意识。
【重点】掌握通过等量代换解决实际问题的方法。
【难点】能够正确的进行等量代换,能够正确的进行逻辑推理。
忆一忆
已知????=2,????=5,????=????+????,求2????+????+????=?
回忆我们学过的知识,想想解决这类问题用什么方法?
因为????=2,????=5,
所以2????=2×2=4,2????+????=9
又已知????=????+????,
所以2????+????+????=19。
这体现的就是等量代换的数学思想。
各代表一个数。
、
、
、
、
+
=
(1)已知
24,
=
+
+
。求 和 的值。
一个 等于三个 的和。
把 + =24中的 换成 + + ,
这叫等量代换。
用等量代换解决实际问题
例1
+
=
24
+ = 24
+
+
等量代换
=
6
=
+
+
=18
4× = 24
代 换
是否等于 ?
+ =160,
+
=160。
已知
两个等式里都有 ☆,可以利用等式的性质。
根据等式的性质,等式两边都减去☆。
可以推出○=160-☆,?=160-☆ 。
因为☆代表同一个数,所以○=? 。
+ =160
+
=160
= 160 -
= 160 -
=
例2
如右图,两条直线相交于点O。
(1)每相邻两个角可以组成一个平角,一共能
组成几个平角?
∠1和∠2, ∠ 2和∠3,∠3和∠4,∠4和∠1,一共能组成4个平角。
平角的两边在一条直线上。
(2)你能推出∠1=∠3吗?
如右图,两条直线相交于点O。
①根据第(1)题的结论,可以得到
∠1+∠2=180°,∠2+∠3=180°。
②根据等式的性质,等式的两边都减去∠2,可以
得到∠1=180°-∠2,∠3=180°-∠2。
③因为180°-∠2=180°-∠2,所以∠1=∠3。
∠1和∠2,,2和∠3,都能组成平角。
这就是等量代换。
1
根据下面的已知条件,求○、□、△的值。
(1) ○+□=91
△+□=63
△+○=46
○=37
□=54
△=9
(2) □-○=8
□+○=12
△=□+□+○
○=2
□=10
△=22
(2)○+□=31 △+○=20
□+△=39
○=( ) △=( )
□=( )
(1)○+△=150 ○= 4×△
○=( ) △=( )
120
30
6
14
25
2
求图形代表的数。
+
已知
=114,
+
+
+
+
=63
+
求 、 的值。
+
=63
+
+
=114,
+
+
+
3 ×
=63
=21
3 × +42
=114
3 ×
=72
=24
3
所以10+ =15
+ =10
因为 + + =15
=5
因为 + =12
所以 =7
因为 + =10
所以 =3
求 、 、 的值。
+ =10, + =12, + + =15。
4
如图中∠1=30°,∠2=50°,求∠3、∠4、∠5的度数。
因为∠1+∠5=180°, ∠1=30°
所以∠5=180° -∠1
=180° -30°
=150°
5
因为∠4+∠5=180°, ∠5=150°
所以∠4=180° -∠5
=180° -150°
=30°
如图中∠1=30°,∠2=50°,求∠3、∠4、∠5的度数。
5
因为∠3+∠2+∠4=180°,
∠4=30° ,∠2=50°
所以∠3=180° -∠4-∠2
=180° -30°-50°
=100°
如图中∠1=30°,∠2=50°,求∠3、∠4、∠5的度数。
5
如图,把三角形ABC的边BC延长到点D。
(1)∠3和∠4拼成的是什么角?(2)你能说∠1+∠2=∠4吗?
(1)∠3和∠4拼成的是平角。
(2)因为∠1+∠2+∠3=180°
∠3+∠4=180°
所以∠1+∠2+∠3=∠3+∠4
两边都减去∠3,可以得到:
∠1+∠2=∠4
6
下课了,谢谢观看
主讲教师:数学老师
2021/小升初数学/总复习/专题复习/教学课件
主讲教师:数学老师
2021/小升初数学/总复习/专题复习/教学课件
考点梳理
Knowledge network
01
考点解析
Question type analysis
02
课时训练
Real exercise
03
知识小结
Knowledge summary
04
CONTENTS
目录
数与代数 第1课时
1.进一步理解整数、分数、小数等的概念,沟通知识之间的联系和区别。
2.深入掌握在直线上表示数,学会简单的识图能力。
3.通过自主探索和合作学习,使学生在整理复习中形成完整的知识体系,掌握复习方法,提高综合运用能力。
【重点】对各种数的意义的理解。
【难点】掌握整理知识的方法,学会系统地看待知识的结构。
理一理
读一读,想一想
第30届夏季奥林匹克运动会于2012年7月27日至8月12日在英国伦敦举行。
你学过哪些数?它们在生活中有哪些应用?阅读下面的资料,你能
发现什么?
读一读,想一想
此次奥运会,来自205个国家和地区的代表队的总计10500名运员参加了26个大项(合302个小项)的比赛。花费4.96亿英镑修建的主体育场“伦敦碗”可容纳8万观众。
中国代表团共有396名运动员(男171名,女225名)参加比赛,约占总运员人数的3.77%。中国获得了38枚金牌、27枚银牌和23枚铜牌,列金牌榜和奖牌榜的第二位,其中金牌数约占总数302枚的八分之一,虽然金牌数比在北京举行的第29届奥运会出现了25.5%的负增长,但仍然取得了中国体育代表团参加在境外举办的历届奥运会的最好成绩。
整数
小数
分数
百分数
负数
数的分类
按不同的标准划分,数的分类也会不同。
分类法一:按正、负数分
数的分类
再来看看第二种分类的方法。
分类法二:按整数与分数、小数分
数的分类
无限小数又可以分为两类。
分类法二:按整数与分数、小数分
数的意义
数的意义
数的意义
分数和百分数的关系:
分数既可以表示一个数,也可以表示两个数的比;而百分数只表示一个数占另一个数的百分比,不能用来表示具体的数。分数后面可以带单位名称,而百分数后面不能带单位名称。
小数:
像0.1、0.2、3.14、10.007……这样用来表示十分之几、百
分之几、千分之几……的数叫做小数。
在直线上表示数
-4 -3 -2 -1 0 1 2 3 4
( )是正数,( )是负数,
( )是自然数,( )是整数。
1,2,3,4
-1,-2,-3,-4
0,1,2,3,4
0,1,2,3,4,-1,-2,-3,-4
-1.5
1.5
( )
( )
在直线上表示数
-4 -3 -2 -1 0 1 2 3 4
3
-3.5
3, ,-3.5,-4。
14
?
-4
14
?
1
你能结合实际说明0.5、 、50%的含义吗?
12
?
0.5表示5个十分之一是多少。
12表示把单位1平均分成2份,其中的1份是多少。
50%表示一个数是另一个数的百分之五十。
?
小数通常表示具体的数量,
如1支铅笔0.5元……
(1)2008年8月3日,我国气象部门在新疆吐鲁番盆地的艾丁湖观测到了我国极端最高气温是49.7℃,可记作 ℃。1969年2月13日,我国气象部门在黑龙江漠河观测到了我国极端最低气温是零下52.3℃,可记作 ℃。
+49.7(或49.7)
-52.3
(2)如果a ÷b=c(a、b、c均为正数,且b≠0),那么a和b的最大公因数是 ,最小公倍数是 。
b
a
(3)一种商品打七折销售,“七折”表示原价的( )%。如果这种商品原价是100元,付款时要少付( )元。
70
30
2
说出下面各数中“2”表示的含义。
23
0.52
23
203.7
?
表示2个十
表示2个百分之一
表示2个三分之一
表示2个百
3
判断
(1)一头野牛重 吨,可以写成25%吨。( )
×
(2)小雨说大于2而小于6的数只有3,4,5。( )
×
4
填空,使每横行的各数相等。
小数
分数
百分数
0.4
80%
40%
0.75
75%
0.8
25
?
45
?
34
?
5
当a为哪些整数时,可以得到下面的答案
(1)在a3中,当a为( )时,a3可以表示自然数的单位。
?
3
(2)在a3中,当a为( )时,a3可以表示真分数。
?
1,2
(3)在a3中,当a为( )时, a3可以表示假分数。
?
大于或等于3的整数
6
数与代数 第2课时
1.进一步掌握十进制计数法,理解数位与计数单位的区别。
2.牢记数位顺序表,利用数位顺序表读数写数,比较数的大小。
3.复习整理因数、倍数的含义,解决因数、倍数在实际问题中的应用。
4.深入理解小数点的移动引起小数大小变化,从而培养学生整理知识的能力。
【重点】牢固掌握数位顺序表。
【难点】理解、掌握小数点的移动引起小数大小的变化。
理一理
计数单位和数位
数位顺序表
整数部分
小
数
点
小数部分
…
( )级
( )级
( )级
数
位
…
位
位
位
位
位
位
位
位
千
位
百
位
十
位
个
位
·
十
分
位
位
位
…
计
数
单
位
…
十
一
(个)
十
分
之
一
…
个
万
亿
万
十
万
百
万
千
万
亿
十
亿
百
亿
千
亿
百
千
万
十
万
百
万
千
万
亿
十
亿
百
亿
千
亿
百
分
千
分
百
分
之
一
千
分
之
一
数的读写、改写
整数的读法、写法
数的读写、改写
分数的读法、写法
读法
整数部分按照整数的读法来读,读完后加上个“又”字;分数部分先读分母,加上“分之”,后面再读分子。
读法
整数部分按照整数的写法来写,“又”字不用写,分数部分先读的是分母,写在下面,后读的是分子,写在上面,中间用分数线隔开。
数的读写、改写
百分数的读法、写法
数的读写、改写
小数的读法、写法
数的读写、改写
大数的改写方法
把多位数改写成用“万”或“亿”作单位的数,在万位或亿位的后面点上小数点,省略小数部分末尾的0,并在后面写上“万”或“亿”字,中间用“=”连接。
省略尾数改写成近似数
用“四舍五入”法省略万位或亿位后面的尾数,并在这个数的后面写“万”或“亿”字,中间用“≈”连接。
小数的近似数
要求把小数保留到哪一位,就把哪一位后面的数用“四舍五入”法省略,中间用“≈”连接。省略尾数改写成近似数。
假分数与带分数、整数之间的互化
假分数化成整数或带分数
例:把123和85改写成整数或带分数。
12÷3=4 123=4
85=135
?
假分数与带分数、整数之间的互化
整数化成假分数
用指定的分母作分母,用整数乘分母的积作分子。
带分数化成假分数
用整数部分乘分母的积加上分数部分的分子作分子,原分母不变。
例:5=5×44=204
623=6×3+23=203
?
数的大小比较
倍数、因数
想想什么是公倍数和公因数呢?
1
判断对错,对的画“√”,错的画“×”。
(1)把0.56扩大到它的100倍是560。 ( )
(2)0是正数。 ( )
(3)假分数的倒数一定都是真分数。 ( )
(4)所有的偶数都是合数。 ( )
(5)a(a>1)的所有因数都小于a。 ( )
×
×
×
×
×
解答问题
(1)写出15,48的因数。
(2)24和36的公因数都有哪些?
15的因数有:1,3,5,15。
48的因数有:1,2,3,4,6,8,12,16,24,48。
24和36的公因数有:1,2,3,4,6,12。
2
一箱苹果有40多个,如果把这箱苹果每8个装一盒,还剩余6个;如果每10个装一盒,也剩余6个。这箱苹果有多少个?
5×8+6=46
10×4+6=46
答:这箱苹果有46个。
3
用 2 、7、4 、5 和5个0写出符合下列要求的数。
最大的九位数:
百万位上是七的最小九位数:
只读出一个零的最小九位数:
个级数位上都是零最小九位数:
754200000
207000045
200000457
204570000
4
第一位是5的最小的倍数,第二位缩小为原来的1100是0.02,第三位是8的最大的因数,第四位是最大的一位自然数,第五位是最小的自然数,第六位是10以内最大的奇数。猜猜这个密码是多少。
?
528909
5
数与代数 第3课时
【重点】能够正确、灵活进行四则混合运算。
【难点】深入掌握四则运算各部分名称之间的关系。
1.进一步理解四则运算的意义,分析在四则运算中0或1参与运算时的特殊情况。
2.深入理解整数、分数、小数四则运算的异同点。帮助学生在辨析学
会整合、理解知识。
3.根据学过的知识整理四则运算中各部分名称之间的关系,利用各部分
名称之间的关系解决实际问题。
理一理
四则运算的运算意义
+
加法
把两个数合成一个数的运算
-
减法
已知两个数的和与其中的一个加数,求另一个加数的运算。
×
乘法
求几个相同加数的和的简便运算。
÷
除法
已知两个乘数的积与其中一个乘数,求另一个乘数的运算。
不同类数(整数、小数、分数)的四则运算的异同
相同点
不同类数(整数、小数、分数)的四则运算的异同
不同点
不同类数(整数、小数、分数)的四则运算的异同
例:计算下面各题。
1260+60=
5700-268=
22.8+1.24=
12+13=
?
450÷3=
15.6×4÷0.2=
1320
5432
24.04
150
312
56
?
0或1参与运算的特殊情况
例: 0+8=0,9-0=9
7×0=0,0÷8=0
0或1参与运算的特殊情况
例:
1×10=10,1÷8=18
?
四则运算各部分之间的关系
26+32=58
58-26=32
58-32=26
2.5×4=10
10÷2.5=4
10÷4=2.5
减法是加法的逆运算
乘法是加法的简便运算
除法是乘法的逆运算
a+a+a+……+a
n个
=a×n
四则运算各部分之间的关系
加数+加数=和
被减数-减数=差
一个加数=和-另一个加数
被减数=减数+差
减数=被减数-差
乘数×乘数=积
被除数÷除数=商
一个乘数=积÷另一个乘数
被除数=商×除数
除数=被除数÷商
四则运算各部分之间的关系
例:根据乘法算式,写出两道除法算式和一道乘法算式。根据加法算式写出两道减法算式和一道加法算式。
26+32=58
125×8=1000
32+26=58
58-26=32
58-32=26
8×125=1000
1000÷8=125
1000÷125=8
四则运算各部分之间的关系
例:根据乘法算式,写出两道除法算式和一道乘法算式。根据加法算式写出两道减法算式和一道加法算式。
1.6+2.7=4.3
2.5×4=10
2.7+1.6=4.3
4.3-2.7=1.6
4.3-1.6=2.7
4×2.5=10
10÷2.5=4
10÷4=2.5
四则运算的顺序
四则运算的顺序
计算,并说说运算顺序。
(128-75)×2
=53×2
=106
45+28÷4
=45+7
=52
47+36+18
=83+18
=101
12.5×8÷10
=100÷10
=10
27+68=
910-540=
95
370
18×40=
720
910÷70=
78-0.8=
13
77.2
3÷12=
6.3÷0.1=
63
36×25%=
9
3
94+34=
?
14
?
口算
1
3?25=
?
56×35=
?
12÷14=
?
3.48+6.52=
1.02-0.43=
10
0.59
0.25×0.8=
0.2
12.6÷3=
4.2
235
?
12
?
2
?
口算
1
(3)0除以任何数都得0。( )
判断对错
(1)做四则混合运算时,先算加减后算乘除。( )
(2)被减数等于减数加差。( )
×
√
×
2
计算
5×47+5×53
=5×(47+53)
=500
(40-13.5)÷14
?
=26.5×4
=106
40÷(15-7)
=40÷8
=5
12.5×(240-480×16)
?
=12.5×(240-80)
=2000
3
数与代数 第4课时
1.复习学过的五种运算定律:加法交换律、加法结合律、乘法交换律、乘法结合律、乘法分配律。
2.灵活运用五种定律在四则混合运算中解决问题。
3.掌握估算的运用原则,了解估算策略,为解决实际问题打好基础。
【重点】牢固掌握运算定律帮助计算。
【难点】运用原有知识解决实际问题。
理一理
运算律
看算式归纳表格
15+28=28+15
65+75+25=65+(75+25)
23×4=4×23
78×125×8=78×(125×8)
8×(125+2)=8×125+8×2
运算律
名称
举例
用字母表示
加法交换律
15+28=28+15
a+b=b+a
加法结合律
乘法交换律
乘法结合律
乘法分配律
65+75+25
=65+(75+25)
a+b+c=a+(b+c)
23×4=4×23
a×b=b×a
78×125×8
=78×(125×8)
a×b×c=a×(b×c)
8×(125+2)
=8×125+8×2
a×(b+c)=a×b+a×c
看算式归纳表格
运算性质
运算性质
例:78.4-12.38-24.62 104÷58÷3215
?
=104÷(58×3215)
?
=78.4-(12.38+24.62)
=78.4-37
=41.4
=104÷43
?
=26
估算策略
估算策略
估算应用
例:完成下面的问题。
(1)7.99×9.99与80比,哪个大?
(2) 12+35比1大吗?
?
(3)妈妈带100元去书店买书,她买了两本文学书,每本20.6元;又花39.6
元买了一本汉语词典;之后,妈妈还想买一本家庭菜谱,有两本菜谱可供选择:薄本的13.7元,厚本的23.8元。请帮妈妈估算一下,这时她的钱够买哪一本?
估算应用
(1)7.99×9.99与80比,哪个大?
把7.99估计成8,把9.99估计成10,8×10=80,但是因为我们利用的是四舍五入法,也就是比五大的就进1,实际上比8和10小,所以结果比80小。
(2) 12+35比1大吗?
?
35比12大,所以看成是两个12相加,结果等于1,所以35比1大。
?
估算应用
(3)妈妈带100元去书店买书,她买了两本文学书,每本20.6元;又花39.6
元买了一本汉语词典;之后,妈妈还想买一本家庭菜谱,有两本菜谱可供选择:薄本的13.7元,厚本的23.8元。请帮妈妈估算一下,这时她的钱够买哪一本?
两本文学书每本估计是21元,两本是42元词典估计是40元,还剩18元,所以只够买薄本的13.7元的菜谱。
1
填一填
(1)27除以6的商是4,余数是3,如果被除数和除数都扩大到原
来的100倍,商是( ),余数是( )。
4
(2)如果a÷b=15……6,那么a最小是( )。
(3)在一个减法算式,差是18,如果被减数不变,减数增加3.2,差( )。
300
111
14.8
457+786+214
=457+(786+214)
=1457
125×16
=125×8×2
=2000
14×59+14×49
?
45?27×59
?
=14×(59+49)
?
=14
?
= 45×59?27?×59
?
=10
?
2
计算下面各题
32+35+25
?
125×24
=125×(8×3)
=125×8×3
=1000×3
=3000
=32+(35+25)
?
=32+1
?
=52
?
2
计算下面各题
六年级有5个班,1至5班的人数依次为:43、 40、41、44、42,学校小礼堂有200个座位,如果召开六年级毕业典礼,需要加椅子吗?
人数最少的班有40人,5个班总人数一定大于200人,需要加椅子。
3
803-207≈
798+205≈
600
1000
23×498≈
10000
632÷69≈
9
4
估算
估一估,在 里填上“>”或“<”
8+75
?
712×397
?
3.7?56
?
59×9.9
60
>
<
32
32÷1.2
57×0.8
57
370
10.1×37
9
2.7
3
49÷1019
?
1
<
>
>
>
>
<
5
0.65×101
=0.65×(100+1)
=0.65×100+0.65×1
=65+0.65
=65.65
0.4×37+0.6×37
?
=(0.4+0.6)×37
?
=1×37
?
=37
?
6
计算
12+13÷25?23
?
23÷89×1?34
?
=56÷25?23
?
=23÷89×14
?
=2512?23
?
=34×14
?
=316
?
=1712
?
6
计算
33338712×79+790×6666114
?
=333387.5×79+790×66661.25
=33338.75×10×79+790×66661.25
=33338.75×790+790×66661.25
=(33338.75+66661.25)×790
=100000×790
=79000000
7
巧算
数与代数 第5课时
1.归纳、总结解决实际问题的主要步骤,从中感受数学的实用性。
2.运用解决实际问题的主要步骤解决实际问题,初步建立学生的社会实践性。
【重点】归纳解决实际问题的主要步骤。
【难点】运用解决问题的主要步骤解决实际问题。
理一理
解决问题归类
相遇
问题
路程÷(甲速+乙速)=相遇时间
(甲速+乙速)×相遇时间=路程
追击
问题
(假设甲速大于乙速)
甲与乙的距离÷(甲速-乙速)=追上时间
(甲速-乙速)×追上时间=甲与乙的距离
工程
问题
工作总量÷工作效率=工作时间
工作总量÷工作时间=工作效率
工作效率×工作时间=工作总量
解决问题归类
和差问题
(和+差)÷2=大数
大数-差=小数
(和-差)÷2=小数
小数+差=大数
和-小数=大数
鸡兔同笼问题
假设全是鸡
(总腿数-总头数×2)÷(4-2)=兔的只数;
假设全是兔
(总头数×4-总腿数)÷(4-2)=鸡的只数。
解决问题归类
求一个数是另一个数的几分之几(或百分之几)。
比较量÷标准量(单位“1”)=分率(百分率)
求一个数的几分之几(或百分之几)是多少。
单位“1”的量× 对应的分率(百分率)=要求的量
求比一个数多(少)几分之几(或百分之几)的数是多少。
标准量× (1 ± 分率或百分率)=比较量(要求的量)
分数/百分数问题
解决问题归类
已知一个数的几分之几(或百分之几)是多少,求这个数。
求一个数比另一个数多(少)几分之几(或百分之几)。
多的量(少的量)÷单位“1”=分率(百分率)
已知一个数比另一个数多或少几分之几或百分之几,求这个数。
已知量÷分率(百分率)=要求的量(单位“1”)
已知量÷分率(百分率)=要求的量(单位“1”)
例:
六年级举行“小发明”比赛,六(1)班同学上交32件作品,六(2)班比六(1)班多交14,两个班共交了多少件作品?
?
六(1)班:
六(2)班:
32件
?件
比六(1)班多
4
1
可以画线段图分析。
例:
六年级举行“小发明”比赛,六(1)班同学上交32件作品,六(2)班比六(1)班多交14,两个班共交了多少件作品?
?
32×1+14=
?
32+40=
?
答:两个班共交了72件作品。
40(件)
72(件)
解决问题的步骤
1
书店第一季度的营业额为15万元,第二季度的营业额为16.5万元。第二季度的营业额比第一季度增长了百分之多少?
16.5-15=1.5(万元)
1.5÷15×100%=10%
答:第二季度的营业额比第一季度增长了10%。
A城开往B城的火车平均每小时行120千米,4小时可以到达;提速
后,平均每小时比原来多行40千米,几小时到达?
120×4=480(千米)
120+40=160(千米)
答:3小时到达。
480÷160=3(小时)
先求路程,再求提速后的速度,最后求时间。
2
女生有150人,男生是女生的 ,男生、女生一共有多少人?
150×45=
?
150+120=
?
270(人)
?
答:男生、女生一共有270人。
120(人)
3
一个旅游公司,去年接待游客24000人,今年比去年减少10%,今年接待游客多少人?
24000×(1-10%)=21600(人)
答:今年接待游客21600人。
4
河东区要修一条640米的景观大道,第一周修了这条路的14,第二周修了这条路的20%,还剩多少米没修?
?
640×(1-14- 20%)
?
=640×0.55
=352(米)
答:还剩352米没修。
先求剩下的占这条路的几分之几,再求剩下多少米没修。
5
学生夏令营组织远足,原计划3小时走完11.25 km。实际2.5小时就走完了原定路程。实际比原计划每小时多走多少千米?
11.25÷2.5-11.25÷3
=4.5-3.75
=0.75(km)
答:实际比原计划每小时多走0.75 km。
6
下表中是G35次列车途径站点的相关信息。你能估算一下这趟列
车在行驶全程中(扣除停留时间)的平均速度大约是多少吗?
7
17:24-11:06-17分≈6(时)
1487÷6≈250(km/h)
答:平均速度大约是250km/h。
7
下表中是G35次列车途径站点的相关信息。你能估算一下这趟列
车在行驶全程中(扣除停留时间)的平均速度大约是多少吗?
1.8+0.6+半臂长>2.6
答:爸爸能换成灯泡。
8
小红家客厅的顶灯需要更换一个灯泡。已知灯泡距地面2.6m,爸爸身高1.80m,小红搬了一个高0.6m的凳子。爸爸能换成灯泡吗?
数与代数 第6课时
1.整理复习用字母表示数、数量关系、计算公式及运算定律,提升学生的自主归纳、整理的能力。
2.理解等式与方程的联系与区别,使学生深刻理解方程的意义,理清解方程的一般步骤,灵活地掌握解方程的方法。
3.在实际问题中掌握列方程解应用题的一般步骤,使学生掌握用方程解决问题,提高学生解决问题的综合实践能力。
【重点】掌握用字母表示数、运算定律及计算公式,灵活解方程。
【难点】利用列方程解应用题的一般步骤解决数学问题。
理一理
用字母表示数
字母表示数量关系
路程=速度×时间
s=vt
总价=单价×数量
c=an
工作总量=工作效率×工作时间
c=at
字母表示计算方法
ba+ca=b+ca
?
用字母表示数
用字母表示运算定律
{5940675A-B579-460E-94D1-54222C63F5DA}名称
用字母表示
加法交换律
加法结合律
乘法交换律
乘法结合律
乘法分配律
a+b=b+a
(a+b)+c=a+(b+c)
a×b=b×a
(a×b)×c=a×(b×c)
(a+b)×c=a×c+b×c
用字母表示数
注意事项
方程
方程
等式的性质
等式的两边同时加上(或减去)同一个数,等式仍然成立;等式的两边同时乘(或除以)同一个数(0除外),等式仍然成立。
例:解方程,说一说什么是解方程,什么是方程的解。
2x+4=20
?
解:
2x=20?4
?
2x=16
?
x=16÷2
?
x=8
?
列方程解应用题
用方程解决问题的步骤
列方程解应用题
列方程解决实际问题的类型
1
小雨今年a岁,比妈妈小23岁,2年后小雨和妈妈的年龄和是多少?
2年后小雨年龄:(a+2)岁
2年后妈妈年龄:(a+23+2)岁
2年后年龄和是:(a+2)+(a+23+2)=(2a+27)岁
写出平行四边形、长方形、正方形、三角形、梯形的面积公式,长方形、正方形的周长公式。
平行四边形面积=底×高,S=ah
长方形面积=长×宽,S=ab
正方形面积=边长×边长,S=a·a=a2
三角形面积=底×高÷2,S=ah÷2
梯形面积=(上底+下底)×高÷2,S=(a+b)h÷2
长方形周长=(长+宽)×2,C=2(a+b)
正方形周长=边长×4,C=4a
2
(1)李奶奶家本月用电a千瓦时,比上个月多用10千瓦时,上个月用电
( )千瓦时。如果每千瓦时电的价格是c元,李奶奶家本月的电费是( )元。李奶奶家银行缴费卡上原有215元,扣除本月电费后,还剩( )元。
(3)小明今年m 岁,妈妈的岁数比她的3倍少6岁。妈妈的岁数是( )岁。如果m=12,妈妈今年是( )岁。
(4)三个连续的自然数,最大的一个是n,那么最小的一个数是( )。
a-10
ac
215-ac
3m-6
30
n-2
填空
3
学校买来9个足球,每个a元,又买来b个篮球,每个58元。
9a表示 ;
58b表示 ;?
58-a表示 ;?
9a+58b表示 ;?
如果a=45,b=6,则9a+58b= 。
9个足球的钱数
b个篮球的钱数
每个篮球比足球贵的钱数
买9个足球和b个篮球共用的钱数
753
4
判断题
(1)所有的等式都是方程,所有的方程不一定都是等式。( )
?
(2)3+4=7是等式,不是方程。 ( )
√
(3)方程的解可以是整数、小数、分数、百分数。( )
√
5
x=13+0.25
?
4+0.7x=102
?
解:
解:
x=712
?
x?0.25=13
?
0.7x=102?4
?
0.7x=98
?
x=98÷0.7
?
x=140
?
解方程
6
x4=30%
?
23x+12x=42
?
解:
解:
x=30%×4
?
x=1.2
?
76x=42
?
x=42÷76
?
x=36
?
解方程
6
绿化队为一个居民社区栽花。栽月季花240棵,再加上16棵就是所栽丁香花棵树的2倍。栽了多少棵丁香花?
7
解:设栽丁香花x棵。
2x=240+16
x=128
答:栽了128棵丁香花。
绿化队为一个居民社区栽花。栽月季花240棵,再加上16棵就是所栽丁香花棵树的2倍。栽了多少棵丁香花?
7
商店卖一种书包,如果每个售价为150元,那么售价的60%是进价,售价的40%就是赚的钱。现在要搞促销活动,为保证一个书包赚的钱不少于30元,应该怎样确定折扣?
答:八折或八折以上。
150×60%=90(元)
90+30=120(元)
120÷150=80%
8
数与代数 第7课时
1.通过比较比和比例各部分名称和基本性质,深刻理解比和比例的意
义,联系及区别。
2.通过回顾正比例关系、反比例关系的概念,使学生正确掌握在生活
事例中对于正比例和反比例的判断方法,在实际问题中能够灵活运用
正比例和反比例解决问题。
【重点】掌握比和比例的意义和性质。
【难点】掌握在生活事例中对于正比例和反比例的判断方法。
理一理
比和比例的联系与区别
{5940675A-B579-460E-94D1-54222C63F5DA}
比
比例
意义
各部分名称
基本性质
两数相除又叫两个数的比。
两个比相等的式子叫作比例。
0.6 :0.8 = 0.75
前项
后项
比值
…
…
…
2 : 3 = 6 : 9
内项
外项
比的前项和后项都乘或除以相同的数(0除外)比值不变。
在比例里,两外项之积等于两内项之积。
化简比的依据
解比例的依据
化简比、求比值
化简比的方法
整数比
小数比
分数比
比的前项和后项同时除以它们的最大公因数。
把比前、后项的小数点向右移动相同的位数,转化成整数比再化简。
把比前、后项同时乘分母的最小公倍数,转化成整数比再化简。
化简比、求比值
{616DA210-FB5B-4158-B5E0-FEB733F419BA}
一般方法
结果
求比值
化简比
根据比值的意义,用前项除
以后项。
结果是一个数,可以是整数、小数或分数。
根据比的基本性质,把比的前项和后项都乘或者除以相同的数(零除外)。
结果是一个比,而且是最简整数比。
求比值和化简比的区别
比、分数、除法之间的联系及区别
{8799B23B-EC83-4686-B30A-512413B5E67A}
比
除法
分数
联 系
区 别
前项
后项
比号
比值
被除数
除号
除数
商
分子
分数线
分母
分数值
比是两个数之间的倍数关系
除法是一种运算
分数是一种数
比、分数、除法之间的联系及区别
比的基本性质、分数的基本性质、商不变的性质三者之间联系及区别
比的基本性质
分数的基本性质
商不变的性质
比的前项和后项同时乘或除以相同的数(0除外),比值不变。
分数的分母和分子同时乘或除以相同的数(0除外),分数的大小不变。
在除法中,被除数和除数同时乘或除以相同的数(0除外),商不变。
商不变的性质、比的基本性质和分数的基本性质的内容实质上是一样的。
比和比例的应用
比例尺
{8799B23B-EC83-4686-B30A-512413B5E67A}
分 类
举 例
意 义
一幅图的图上距离和实际距离的比。
按表现形式,可以分为数值比例尺和线段比例尺。
按将实际距离放大还是缩小分,分为缩小比例尺和放大比例尺。
1:500000
0
50km
1:500000
20:1
比和比例的应用
解决按比分配问题的解题步骤
{5940675A-B579-460E-94D1-54222C63F5DA}名称
联系
区别
变化规律
关系式
图像
正比例
反比例
比和比例的应用
正比例和反比例
1.两种相关联的量。
2.一种量随着另一种量的变化而变化。
相对应的两个量的比值(商)一定。
相对应的两个量的积一定。
y:x=k
(一定)
xy=k
(一定)
1
(1)7÷8可以写成( )。
(2)( )叫方程。
含有未知数的等式
(3)2∶4=( )∶12。
6
(4)在比例里,两个内项的积是70,两个外项的积是( )。
70
填空
7:8或78
?
判断下面两种量是否成比例,成什么比例?
(1)爸爸上班的路程一定,速度和时间。
(2)故事书的总页数一定,看的页数和剩余的页数。
(3)单价一定,总价和数量。
(4)三角形的面积一定,三角形的底与底边上的高。
(1)成比例,成反比例
(2)不成比例
(3)成比例,成正比例
(4)成比例,成反比例
2
判断题
(1)甲数除以乙数的商是1.4,甲数和乙数的比是7∶5。 ( )
(2)π是圆的周长与直径的比值。 ( )
(3)甲、乙两人同时从A地到B地,甲6小时到达,乙5小时到达。甲、乙所用的时间的比和速度的比都是6∶5。 ( )
(4)在比例中,两个外项的积除以两个内项的积,商是0。 ( )
(5)因为3×10=5×6,所以3:5=10:6。 ( )
(6) 18:30和3:5可以组成比例。 ( )
√
×
√
×
×
√
3
伦敦奥运会一块金牌的黄金含量与金牌总重的比为6:412。一块金牌总重412 g,302块金牌需要黄金多少克?
答:302块金牌需要黄金1812克。
412×6412=
?
6×302=
?
6(克)
1812(克)
4
北京到济南高速公路距离大约为430 km,北京到天津大约为120 km。一辆汽车从北京出发开往济南,当行驶到天津时用了1.5小时。按照这个速度,北京到济南全程需要多少小时?
答:北京到济南全程需要5.375小时。
解:设需要x小时。
430x=1201.5
?
x=5.375
?
5
同一幅地图上,量得甲、乙两地的直线距离是20cm,甲、丙两地的直线距离是12 cm。如果甲、乙两地的实际距离是1600 km,那么甲、丙两地的实际距离是多少?
答:甲、丙两地的实际距离是960 km。
解:设甲、丙两地的实际距离为x km。
201600=12x
?
x=960
?
6
六年级(2)班乘车去农家果园采摘草莓,汽车以40千米/时的速度行驶1小时到达果园,在果园活动了2小时,然后乘车以相同的速度返回。观察下面两幅图象,它们有什么不同?
返回时汽车行驶的路程不断增加,而离校距离越来越近(少),与来时的方向相反。
7
数与代数 第8课时
1.复习利用数形结合寻找规律解决实际问题的方法。
2.进一步巩固、发展学生找规律的能力,体会找规律对解决问题的重要性及数形结合数学思想的重要性。
3. 激发学生学习数学、探索规律的兴趣。提高学生的合作意识。
【重点】复习利用数形结合寻找规律解决问题的方法。
【难点】能够正确的利用数形结合法分析归纳出规律。
忆一忆
回忆我们学过的知识,想想解决这类问题用什么方法?
……
如下图,摆1个正方形需用4根小棍,摆2个正方形需用7根小棍,摆
3个正方形需用10根小棍,照这样摆下去,第n个图形需用多少根小
棍?
找规律。
第n个图形需用4+3(n-1)根小棍
找规律
例:每两个点连成一条线段,一共可以连成多少条线段呢?
有什么规律呢?
{5DA37D80-6434-44D0-A028-1B22A696006F}点数
增加条数
总条数
A
B
A
B
1
我们通过画图来看看!
{5DA37D80-6434-44D0-A028-1B22A696006F}点数
增加条数
总条数
1
A
B
C
A
B
A
B
C
2
3
{5DA37D80-6434-44D0-A028-1B22A696006F}点数
增加条数
2
总条数
1
3
A
B
C
A
B
C
D
A
B
C
D
A
B
3
6
A
B
C
D
E
{5DA37D80-6434-44D0-A028-1B22A696006F}点数
增加
条数
2
3
总条数
1
3
6
A
B
C
D
A
B
C
A
B
C
D
E
A
B
4
10
3个点共连:1+2=3(条)
4个点共连:1+2+3=6(条)
{5DA37D80-6434-44D0-A028-1B22A696006F}点数
2个点
3个点
4个点
5个点
6个点
增加
条数
2
3
4
总条数
1
3
6
10
5个点共连:1+2+3+4=10(条)
5
15
6个点共连:1+2+3+4+5=15(条)
你在你有什么发现吗?
{5DA37D80-6434-44D0-A028-1B22A696006F}点数
2个点
3个点
4个点
5个点
6个点
增加
条数
2
3
4
总条数
1
3
6
10
5
15
有几个点,增加的条数比点数少1。
计算有几条线段,就是从1+2+3+…一直加到比点数少1的
数再求和就可以了。
n个点
12个点共连
20个点共连
根据规律,你知道12个点、20个点能连成多少条线段?请写出算式。
1+2+3+4+5+6+7+8+9+10+11=66(条)
1+2+3+…+19=190(条)
1+2+3+…+(n-1)=n(n-1)÷2
和=(首项+末项)×项数÷2
这种算式叫做等差数列。
(1)
(2)
(3)
(4)
(1)第7幅图有多少个棋子?第15幅图呢?
1 4 9 16
观察下图,想一想。
7×7=49(个)
15×15=225(个)
答:第7幅图有49个棋子,第15幅图有225个棋子。
1
(1)
(2)
(3)
(4)
(2) 每边的棋子数与图形的序号有什么关系?
{5940675A-B579-460E-94D1-54222C63F5DA}
图形的序号
每边的棋子数
1
2
1
4
3
2
3
4
……
……
答:每边的棋子数与图形的序号相等。
1
{5940675A-B579-460E-94D1-54222C63F5DA}
(1)
(2)
(3)
(4)
图形的序号
每边的棋子数
1
2
1
4
3
2
3
4
……
……
(3)第n幅图每边有多少个棋子?一共有多少个棋子?
每行的棋子数×行数=棋子总数
n×n=棋子总数
n2=棋子总数
n
n
答:第n幅图每边有n个棋子,一共有n2个棋子。
1
摆一摆,找规律。
(1)第6个图形是什么图形?
答:第6个图形是平行四边形。
2
(2)摆第7个图形需要用多少根小棒?
答:需要用15根小棒。
摆一摆,找规律。
2
(3)摆第n个图形需要用多少根小棒?
答:需要用2n+1根小棒。
摆一摆,找规律。
2
(1)多边形的内角和与它的边数有什么关系?
答:多边形的内角和等于边数减2,再乘180°。
{5940675A-B579-460E-94D1-54222C63F5DA}多边形
……
边数
3
4
5
6
……
内角和
180°
360°
……
3
(2)一个九边形的内角和是多少度?
答:九边形的内角和是1260°。
{5940675A-B579-460E-94D1-54222C63F5DA}多边形
……
边数
3
4
5
6
……
内角和
180°
360°
……
3
(3)一个n边形的内角和是多少度?
答:n边形的内角和是180°×(n-2)。
{5940675A-B579-460E-94D1-54222C63F5DA}多边形
……
边数
3
4
5
6
……
内角和
180°
360°
……
3
数与代数 第9课时
1.复习通过列表格推理从而解决实际问题的方法。
2.进一步发展逻辑推理能力和解决问题的能力,体会列表法对解决问题的重要性。
3. 激发学生学习数学、解决数学问题的兴趣。提高学生的合作意识。
【重点】熟练掌握列表法解决实际问题的方法。
【难点】列出表格后能够正确的进行逻辑推理并解决问题。
忆一忆
学校秋季运动会乒乓球比赛项目中有甲、乙、丙、丁四位同学参加,比赛规则要求四位选手彼此见面,总共需要进行多少场比赛?
回忆我们学过的知识,想想解决这类问题用什么方法?
可以用列表法。
总共需要进行6场比赛。
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
甲
乙
丙
丁
甲
√
√
√
乙
√
√
丙
√
丁
例:
六年级有三个班,每班有2个班长。开班长会时,每次每班只要一个班长参加。第一次到会的有A、B、C;第二次有B、D、E;第三次有A、E、F。请问:哪两位班长是同班的?
列表法解决问题
怎样才能有序思考呢?
例:
六年级有三个班,每班有2个班长。开班长会时,每次每班只要一个班长参加。第一次到会的有A、B、C;第二次有B、D、E;第三次有A、E、F。请问:哪两位班长是同班的?
{8799B23B-EC83-4686-B30A-512413B5E67A}
A
B
C
D
E
F
第一次
1
1
1
0
0
0
第二次
第三次
0
1
0
1
1
0
1
0
0
0
1
1
用数字“1”表示到会
用数字“0”表示没到会
{8799B23B-EC83-4686-B30A-512413B5E67A}??
A
B
C
D
E
F
第一次
第二次
第三次
1
1
0
0
0
1
1
1
0
0
0
1
0
0
1
1
1
0
提示:开班长会时,每次每班只要一个班长参加。
例:
六年级有三个班,每班有2个班长。开班长会时,每次每班只要一个班长参加。第一次到会的有A、B、C;第二次有B、D、E;第三次有A、E、F。请问:哪两位班长是同班的?
那一起参加班会的一定不在同一班级。有且只有一个班长参加。
例:
六年级有三个班,每班有2个班长。开班长会时,每次每班只要一个班长参加。第一次到会的有A、B、C;第二次有B、D、E;第三次有A、E、F。请问:哪两位班长是同班的?
{8799B23B-EC83-4686-B30A-512413B5E67A}??
A
B
C
D
E
F
第一次
第二次
第三次
1
1
0
0
0
1
1
1
0
0
0
1
0
0
1
1
1
0
1
√
√
√
√
√
0
1
√
A和谁可能是同班?
{8799B23B-EC83-4686-B30A-512413B5E67A}??
A
B
C
D
E
F
第一次
第二次
第三次
1
1
0
0
0
1
1
1
0
0
0
1
0
0
1
1
1
0
1
√
√
√
√
√
0
1
√
第一次:A只可能和D、E、
F同班。
第二次:A只可能和D、E同班。
第三次:A只可能和D同班。
例:
六年级有三个班,每班有2个班长。开班长会时,每次每班只要一个班长参加。第一次到会的有A、B、C;第二次有B、D、E;第三次有A、E、F。请问:哪两位班长是同班的?
例:
六年级有三个班,每班有2个班长。开班长会时,每次每班只要一个班长参加。第一次到会的有A、B、C;第二次有B、D、E;第三次有A、E、F。请问:哪两位班长是同班的?
{8799B23B-EC83-4686-B30A-512413B5E67A}??
A
B
C
D
E
F
第一次
第二次
第三次
1
1
0
0
0
1
1
1
0
0
0
1
0
0
1
1
1
0
1
√
√
√
1
B、C可能和谁是同班?
{8799B23B-EC83-4686-B30A-512413B5E67A}??
A
B
C
D
E
F
第一次
第二次
第三次
1
1
0
0
0
1
1
1
0
0
0
1
0
0
1
1
1
0
1
√
√
√
1
A和D同班,则B只可能和E、F同班,根据第二轮推测,B和F同班,据此可推出C、E同班。
例:
六年级有三个班,每班有2个班长。开班长会时,每次每班只要一个班长参加。第一次到会的有A、B、C;第二次有B、D、E;第三次有A、E、F。请问:哪两位班长是同班的?
请问:他们的职业各是什么?
王阿姨、刘阿姨、丁叔叔、李叔叔分别是工人、教师、军人。王阿姨是教师;丁叔叔不是工人;只有刘阿姨和李叔叔的职业相同。
王阿姨
刘阿姨
丁叔叔
李叔叔
工人
教师
军人
√
×
×
√
×
×
√
√
答:王阿姨是教师,丁叔叔是军人,刘阿姨和李叔叔都是工人。
1
学校组织了足球,航模和电脑兴趣小组,淘气、笑笑和小明分别参加了其中一项。笑笑不喜欢踢足球,小明没有参加电脑小组,淘气喜欢航模。他们分别在哪个小组。
足球
航模
电脑
淘气
笑笑
小明
×
×
×
×
×
×
√
√
√
答:淘气在航模小组, 笑笑在电脑小组,小明在足球小组。
2
球场休息时,保管员慌忙中把甲、乙、丙三个运动员先前交给他的水瓶都递送错了,结果甲喝的是丙的。乙、丙各喝的是谁的?
甲
乙
丙
甲的水
乙的水
丙的水
×
√
×
×
×
×
√
√
答:乙喝的是甲的,丙喝的是乙的。
×
3
下图中一共有几条线段?
或7×(7-1)÷2=21(条)
(7-1)+5+4+3+2+1=21(条 )
4
小明、小莉、小刚、小芳四个好朋友站成一排拍毕业纪念照,要求男女间隔排列,一共有多少种站法?
(5)小莉 小明 小芳 小刚
(6)小莉 小刚 小芳 小明
(7)小芳 小明 小莉 小刚
(8)小芳 小刚 小莉 小明
(1)小明 小莉 小刚 小芳
(2)小明 小芳 小刚 小莉
(3)小刚 小莉 小明 小芳
(4)小刚 小芳 小明 小莉
答:共有8种不同的站法。
5
方法一:用列举法
B1 B2
小明 小刚 小莉 小芳
A1 A2 B1 B2
第一位 第二位 第三位 第四位
A1 A2
答:共有8种不同的站法。
2×4=8
互换
互换
小明、小莉、小刚、小芳四个好朋友站成一排拍毕业纪念照,要求男女间隔排列,一共有多少种站法?
方法一:用字母表示法
5
警察抓住了4个偷东西的嫌疑人,其中的一个人是主谋。审问谁是主谋时,甲说:我不是主谋。乙说:丁是主谋。丙说:我不是主谋。
丁说:甲是主谋。已知他们4人中只有一个人说了真话。主谋是谁?
{93296810-A885-4BE3-A3E7-6D5BEEA58F35}
甲
乙
丙
丁
是否
真话
否
是
是
是
结论
主谋
非主谋
非主谋
主谋
是否
真话
是
否
否
否
结论
非主谋
非主谋
主谋
非主谋
通过列表,结合题目信息可知丙是主谋。
6
数与代数 第10课时
1.复习通过等量代换从而解决实际问题的方法,复习简单的几何证
明方法。
2.进一步发展逻辑推理能力和解决问题的能力,体会等量代换对解决
问题的重要性。
3. 激发学生学习数学、解决数学问题的兴趣。提高学生的合作意识。
【重点】掌握通过等量代换解决实际问题的方法。
【难点】能够正确的进行等量代换,能够正确的进行逻辑推理。
忆一忆
已知????=2,????=5,????=????+????,求2????+????+????=?
回忆我们学过的知识,想想解决这类问题用什么方法?
因为????=2,????=5,
所以2????=2×2=4,2????+????=9
又已知????=????+????,
所以2????+????+????=19。
这体现的就是等量代换的数学思想。
各代表一个数。
、
、
、
、
+
=
(1)已知
24,
=
+
+
。求 和 的值。
一个 等于三个 的和。
把 + =24中的 换成 + + ,
这叫等量代换。
用等量代换解决实际问题
例1
+
=
24
+ = 24
+
+
等量代换
=
6
=
+
+
=18
4× = 24
代 换
是否等于 ?
+ =160,
+
=160。
已知
两个等式里都有 ☆,可以利用等式的性质。
根据等式的性质,等式两边都减去☆。
可以推出○=160-☆,?=160-☆ 。
因为☆代表同一个数,所以○=? 。
+ =160
+
=160
= 160 -
= 160 -
=
例2
如右图,两条直线相交于点O。
(1)每相邻两个角可以组成一个平角,一共能
组成几个平角?
∠1和∠2, ∠ 2和∠3,∠3和∠4,∠4和∠1,一共能组成4个平角。
平角的两边在一条直线上。
(2)你能推出∠1=∠3吗?
如右图,两条直线相交于点O。
①根据第(1)题的结论,可以得到
∠1+∠2=180°,∠2+∠3=180°。
②根据等式的性质,等式的两边都减去∠2,可以
得到∠1=180°-∠2,∠3=180°-∠2。
③因为180°-∠2=180°-∠2,所以∠1=∠3。
∠1和∠2,,2和∠3,都能组成平角。
这就是等量代换。
1
根据下面的已知条件,求○、□、△的值。
(1) ○+□=91
△+□=63
△+○=46
○=37
□=54
△=9
(2) □-○=8
□+○=12
△=□+□+○
○=2
□=10
△=22
(2)○+□=31 △+○=20
□+△=39
○=( ) △=( )
□=( )
(1)○+△=150 ○= 4×△
○=( ) △=( )
120
30
6
14
25
2
求图形代表的数。
+
已知
=114,
+
+
+
+
=63
+
求 、 的值。
+
=63
+
+
=114,
+
+
+
3 ×
=63
=21
3 × +42
=114
3 ×
=72
=24
3
所以10+ =15
+ =10
因为 + + =15
=5
因为 + =12
所以 =7
因为 + =10
所以 =3
求 、 、 的值。
+ =10, + =12, + + =15。
4
如图中∠1=30°,∠2=50°,求∠3、∠4、∠5的度数。
因为∠1+∠5=180°, ∠1=30°
所以∠5=180° -∠1
=180° -30°
=150°
5
因为∠4+∠5=180°, ∠5=150°
所以∠4=180° -∠5
=180° -150°
=30°
如图中∠1=30°,∠2=50°,求∠3、∠4、∠5的度数。
5
因为∠3+∠2+∠4=180°,
∠4=30° ,∠2=50°
所以∠3=180° -∠4-∠2
=180° -30°-50°
=100°
如图中∠1=30°,∠2=50°,求∠3、∠4、∠5的度数。
5
如图,把三角形ABC的边BC延长到点D。
(1)∠3和∠4拼成的是什么角?(2)你能说∠1+∠2=∠4吗?
(1)∠3和∠4拼成的是平角。
(2)因为∠1+∠2+∠3=180°
∠3+∠4=180°
所以∠1+∠2+∠3=∠3+∠4
两边都减去∠3,可以得到:
∠1+∠2=∠4
6
下课了,谢谢观看
主讲教师:数学老师
2021/小升初数学/总复习/专题复习/教学课件
同课章节目录
