1.1共点力平衡条件的应用 课件(共38张PPT)
文档属性
| 名称 | 1.1共点力平衡条件的应用 课件(共38张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 物理 | ||
| 更新时间 | 2021-05-27 16:52:17 | ||
图片预览







文档简介
(共38张PPT)
1.1
共点力作用下的平衡问题
知识点回顾:
01
02
03
04
常用方法
动态平衡问题
定义及条件
临界和极值问题
2.平衡态
(1)静止:物体的速度和加速度都等于零的状态。
(2)匀速直线运动:物体的速度不为零,其加速度为零的状态。
1.
共点力平衡:指受力物体在多个力作用下处于静止、匀速直线运动或缓慢运动状态,利用平行四边形定则、合成法与分解法求解力的大小、方向及分析其变化情况的一类问题。
定义及条件
01
定义及条件
01
3.平衡条件
(1)物体所受合外力为零,即F合=0。
(2)若采用正交分解法,平衡条件表达式为Fx=0,Fy=0。
4.物体平衡条件的相关推论
(1)二力平衡:如果物体在两个共点力的作用下处于平衡状态,这两个力必定大小相等,方向相反。
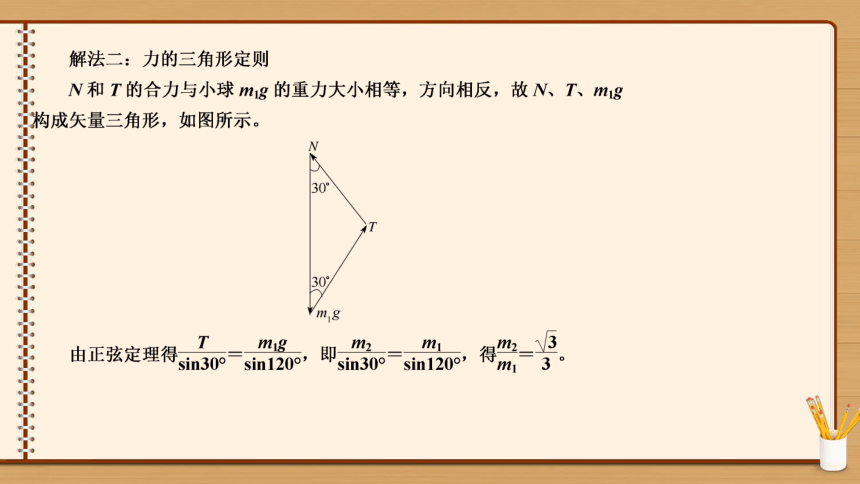
(2)三力平衡:如果物体在三个共点力的作用下处于平衡状态,其中任意两个力的合力一定与第三个力大小相等、方向相反。
(3)多力平衡:如果物体受多个力作用处于平衡状态,其中任何一个力与其余力的合力大小相等,方向相反。
定义及条件
01
特别提醒 物体的速度等于零不同于静止,物体静止时(v=0,a=0)处于平衡状态,而物体只是速度等于零,不一定处于平衡态,如物体竖直上抛到最高点和单摆摆球及弹簧振子在最大位移处时,速度均等于零,但加速度不等于零,不处于平衡态。
02
常用方法
方法
内容
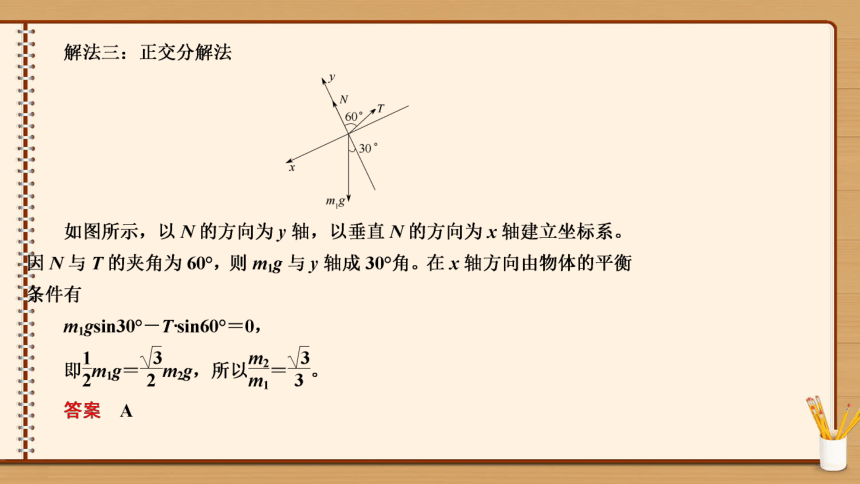
正交
分解法
将处于平衡状态的物体所受的力分解为相互正交的两组,每一组的力都满足力的平衡条件
力的三
角形法
物体受同一平面内三个互不平行的力的作用平衡时,这三个力的矢量箭头首尾相接,构成一个矢量三角形,则这三个力的合力为零;反之,若不能构成三角形,则这三个力的合力必不为零。利用三角形法,根据正弦定理、余弦定理或相似三角形等数学知识可求得未知力
02
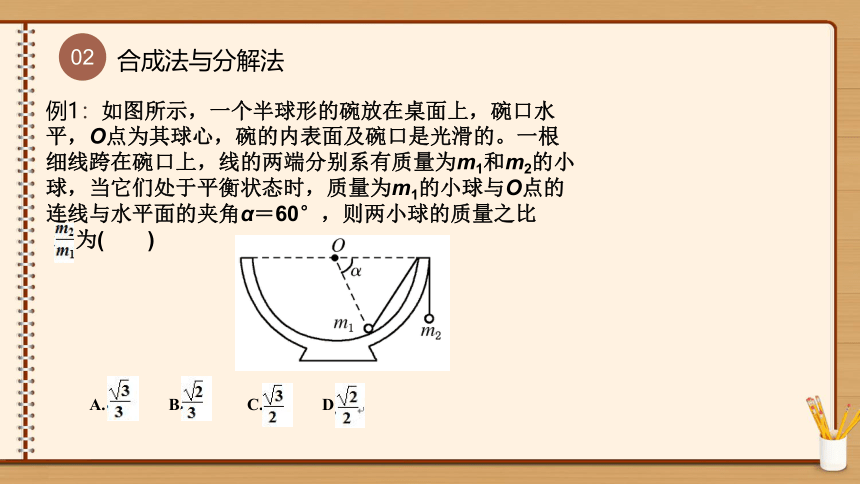
合成法与分解法
例1:如图所示,一个半球形的碗放在桌面上,碗口水平,O点为其球心,碗的内表面及碗口是光滑的。一根细线跨在碗口上,线的两端分别系有质量为m1和m2的小球,当它们处于平衡状态时,质量为m1的小球与O点的连线与水平面的夹角α=60°,则两小球的质量之比
为( )
A.
B.
C.
D.
02
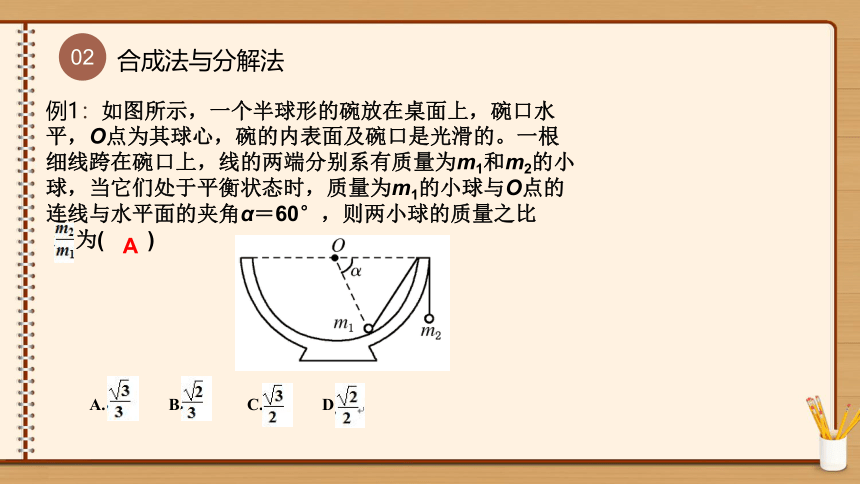
合成法与分解法
例1:如图所示,一个半球形的碗放在桌面上,碗口水平,O点为其球心,碗的内表面及碗口是光滑的。一根细线跨在碗口上,线的两端分别系有质量为m1和m2的小球,当它们处于平衡状态时,质量为m1的小球与O点的连线与水平面的夹角α=60°,则两小球的质量之比
为( )
A.
B.
C.
D.
A
02
合成法与分解法
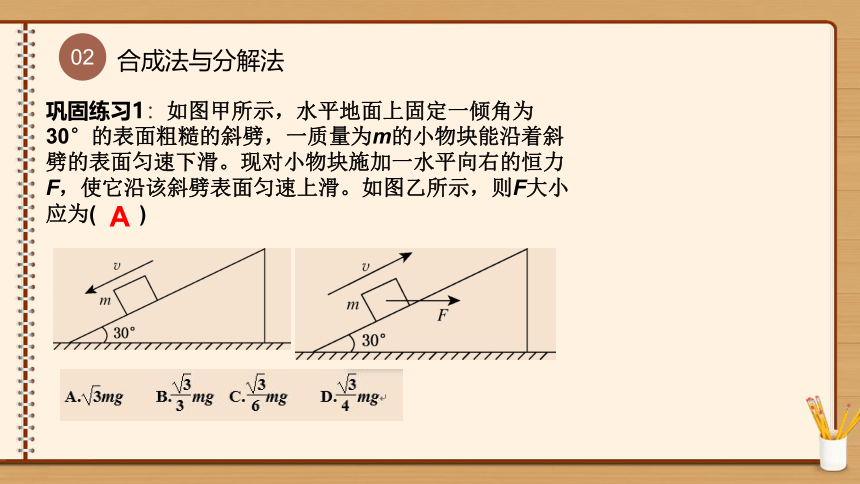
巩固练习1:如图甲所示,水平地面上固定一倾角为30°的表面粗糙的斜劈,一质量为m的小物块能沿着斜劈的表面匀速下滑。现对小物块施加一水平向右的恒力F,使它沿该斜劈表面匀速上滑。如图乙所示,则F大小应为( )
A
03
动态平衡问题
1.动态平衡:通过控制某些物理量,使物体的状态发生缓慢的变化,而在这个过程中物体又始终处于一系列的平衡状态,在问题的描述中常用“缓慢”等语言叙述。
2.处理动态平衡问题的一般思路
(1)平行四边形定则是基本方法,但也要根据实际情况采用不同的方法,若出现直角三角形,常用三角函数表示合力与分力的关系。
(2)图解法的适用情况
图解法分析物体动态平衡问题时,一般物体只受三个力作用.
03
动态平衡问题
3.几种常见情况
①一力不变,一力方向不变的三力动态平衡
②一力不变,两力方向都变的三力动态平衡
③一力不变,另两力夹角保持不变的三力动态平衡
03
一力不变,一力方向不变的三力动态平衡
例2:光滑斜面上安装一光滑挡板AO,挡板可绕O处铰链无摩擦转动,在挡板与斜面间放一匀质球,现使挡板从图示位置缓慢转到竖直位置,此过程中球对挡板的压力N1和球对斜面的压力N2的变化情况?
解析:在缓慢转动过程中,选位置1、2、3,可直观判断N1先减小,后增大;N2一直在增大。
巩固练习2:半圆柱体P放在粗糙的水平地面上,其右端有一固定放置的竖直挡板MN。在半圆柱体P和MN之间放有一个光滑均匀的小圆柱体Q,整个装置处于静止。如图所示是这个装置的纵截面图。若用外力先使MN保持竖直,然后缓慢地水平向右移动,在Q落到地面以前,发现P始终保持静止。在此过程中,下列说法正确的是( )
03
一力不变,一力方向不变的三力动态平衡
A.MN对Q的弹力逐渐增大
B.Q所受的合力逐渐增大
C.P、Q间的弹力先减小后增大
D.地面对P的摩擦力逐渐减小
A.MN对Q的弹力逐渐增大
B.Q所受的合力逐渐增大
C.P、Q间的弹力先减小后增大
D.地面对P的摩擦力逐渐减小
巩固练习2:半圆柱体P放在粗糙的水平地面上,其右端有一固定放置的竖直挡板MN。在半圆柱体P和MN之间放有一个光滑均匀的小圆柱体Q,整个装置处于静止。如图所示是这个装置的纵截面图。若用外力先使MN保持竖直,然后缓慢地水平向右移动,在Q落到地面以前,发现P始终保持静止。在此过程中,下列说法正确的是( )
03
一力不变,一力方向不变的三力动态平衡
A.MN对Q的弹力逐渐增大
B.Q所受的合力逐渐增大
C.P、Q间的弹力先减小后增大
D.地面对P的摩擦力逐渐减小
A
03
一力不变,两力方向都变的三力动态平衡
例3:如图所示为一简易起重装置,AC是上端带有滑轮的固定支架,BC为质量不计的轻杆,杆的一端C用较链固定在支架上,另一端B悬挂一个质量为m的重物,并用钢丝绳跨过滑轮A连接在卷扬机上.开始时,杆BC与AC的夹角∠BCA>90°,现使∠BCA缓缓变小,直到∠BCA=30°.在此过程中,杆BC所受的力及钢丝绳的拉力的变化情况(不计一切摩擦阻力)?
解析:受力分析,构建矢量三角形,与△ABC相似,对应边成比例,可得,由于比值恒定且G不变,∠BCA
变小过程中,AC边、BC边不变,AB边变小,可得杆的支持力不变,绳的拉力变小。
巩固练习3:如图所示,质量均为m的小球A、B用劲度系数为k1的轻弹簧相连,B球用长为L的细绳悬于O点,A球固定在O点正下方,当小球B平衡时,绳子所受的拉力为T1,弹簧的弹力为F1;现把A、B间的弹簧换成原长相同但劲度系数为k2(k2>k1)的另一轻弹簧,在其他条件不变的情况下仍使系统平衡,此时绳子所受的拉力为T2,弹簧的弹力为F2,则下列关于T1与T2、F1与F2之间的大小关系正确的是( )
03
一力不变,两力方向都变的三力动态平衡
A.T1>T2
B.T1=T2
C.F1D.F1=F2
由三角形相似得
巩固练习3:如图所示,质量均为m的小球A、B用劲度系数为k1的轻弹簧相连,B球用长为L的细绳悬于O点,A球固定在O点正下方,当小球B平衡时,绳子所受的拉力为T1,弹簧的弹力为F1;现把A、B间的弹簧换成原长相同但劲度系数为k2(k2>k1)的另一轻弹簧,在其他条件不变的情况下仍使系统平衡,此时绳子所受的拉力为T2,弹簧的弹力为F2,则下列关于T1与T2、F1与F2之间的大小关系正确的是( )
03
一力不变,两力方向都变的三力动态平衡
A.T1>T2
B.T1=T2
C.F1D.F1=F2
BC
03
一力不变,另两力夹角保持不变的三力动态平衡
例3:【2017·全国新课标Ⅰ卷】如图,柔软轻绳ON的一端O固定,其中间某点M拴一重物,用手拉住绳的另一端N。初始时,OM竖直且MN被拉直,OM与MN之间的夹角为
(
)。现将重物向右上方缓慢拉起,并保持夹角
不变。在OM由竖直被拉到水平的过程中(
)
A.MN上的张力逐渐增大
B.MN上的张力先增大后减小
C.OM上的张力逐渐增大
D.OM上的张力先增大后减小
法一:解析法(正弦定理)
矢量三角形中,分别设角θ、β、γ,根据正弦定理有,由题意可知,γ=180°-
α不变,β先增大后减小,θ逐渐增大,故当β=90°时,OM上的张力最大,MN上的张力逐渐增大。
法二:作图法(矢量三角形)
三力合力为零,能构成封闭的三角形,
再借助圆,同一圆弧对应圆周角(γ=180°-α)不变。
P点沿圆弧顺时针方向旋转的过程中,当FOM过直径时最大,而FMN一直增大。
法三:转换法(等效法)
等效细绳OM、MN不动,重力G逆时针旋转90°,同样利用作图法能够判断出OM上的张力先增大后减小,而MN上张力一直增大。
?
03
一力不变,另两力夹角保持不变的三力动态平衡
例3:【2017·全国新课标Ⅰ卷】如图,柔软轻绳ON的一端O固定,其中间某点M拴一重物,用手拉住绳的另一端N。初始时,OM竖直且MN被拉直,OM与MN之间的夹角为
(
)。现将重物向右上方缓慢拉起,并保持夹角
不变。在OM由竖直被拉到水平的过程中(
)
A.MN上的张力逐渐增大
B.MN上的张力先增大后减小
C.OM上的张力逐渐增大
D.OM上的张力先增大后减小
AD
04
临界和极值问题
1.临界问题
当某物理量变化时,会引起其他几个物理量的变化,从而使物体所处的平衡状态“恰好出现”或“恰好不出现”,在问题描述中常用“刚好”“刚能”“恰好”等语言叙述。
2.极值问题
平衡物体的极值,一般是指在力的变化过程中的最大值和最小值问题。
04
临界和极值问题
3.解题思路
解决共点力平衡中的临界、极值问题“四字诀”
例4:将两个质量均为m的小球a、b用细线相连后,再用细线悬挂于O点,如图所示。用力F拉小球b,使两个小球都处于静止状态,且细线Oa与竖直方向的夹角保持θ=30°,则F达到最小值时Oa绳上的拉力为( )
04
临界和极值问题
整体为研究对象,分析受力,作出F在三个方向时整体的受力图,根据平衡条件得知:F与T的合力与重力mg总是大小相等、方向相反,由力的合成图可知,当F与绳子Oa垂直时,F有最小值,即图中2位置,F有最小值,根据平衡条件得F=2mgsin30°=mg,T=2mgcos30°=
mg。
例4:将两个质量均为m的小球a、b用细线相连后,再用细线悬挂于O点,如图所示。用力F拉小球b,使两个小球都处于静止状态,且细线Oa与竖直方向的夹角保持θ=30°,则F达到最小值时Oa绳上的拉力为( )
04
临界和极值问题
A
直击高考
直击高考练习
【2016·全国新课标Ⅱ卷】质量为m的物体用轻绳AB悬挂于天花板上。用水平向左的力F缓慢拉动绳的中点O,如图所示。用T
表示绳OA段拉力的大小,在O点向左移动的过程中(
)
A.F逐渐变大,T逐渐变大
B.F逐渐变大,T逐渐变小
C.F逐渐变小,T逐渐变大
D.F逐渐变小,T逐渐变小
直击高考:
A
【2017·新课标Ⅱ卷】如图,一物块在水平拉力F的作用下沿水平桌面做匀速直线运动。若保持F的大小不变,而方向与水平面成60°角,物块也恰好做匀速直线运动。物块与桌面间的动摩擦因数为(
)
直击高考:
C
感谢观看
THANK
YOU
FOR
WATCHING
1.1
共点力作用下的平衡问题
知识点回顾:
01
02
03
04
常用方法
动态平衡问题
定义及条件
临界和极值问题
2.平衡态
(1)静止:物体的速度和加速度都等于零的状态。
(2)匀速直线运动:物体的速度不为零,其加速度为零的状态。
1.
共点力平衡:指受力物体在多个力作用下处于静止、匀速直线运动或缓慢运动状态,利用平行四边形定则、合成法与分解法求解力的大小、方向及分析其变化情况的一类问题。
定义及条件
01
定义及条件
01
3.平衡条件
(1)物体所受合外力为零,即F合=0。
(2)若采用正交分解法,平衡条件表达式为Fx=0,Fy=0。
4.物体平衡条件的相关推论
(1)二力平衡:如果物体在两个共点力的作用下处于平衡状态,这两个力必定大小相等,方向相反。
(2)三力平衡:如果物体在三个共点力的作用下处于平衡状态,其中任意两个力的合力一定与第三个力大小相等、方向相反。
(3)多力平衡:如果物体受多个力作用处于平衡状态,其中任何一个力与其余力的合力大小相等,方向相反。
定义及条件
01
特别提醒 物体的速度等于零不同于静止,物体静止时(v=0,a=0)处于平衡状态,而物体只是速度等于零,不一定处于平衡态,如物体竖直上抛到最高点和单摆摆球及弹簧振子在最大位移处时,速度均等于零,但加速度不等于零,不处于平衡态。
02
常用方法
方法
内容
正交
分解法
将处于平衡状态的物体所受的力分解为相互正交的两组,每一组的力都满足力的平衡条件
力的三
角形法
物体受同一平面内三个互不平行的力的作用平衡时,这三个力的矢量箭头首尾相接,构成一个矢量三角形,则这三个力的合力为零;反之,若不能构成三角形,则这三个力的合力必不为零。利用三角形法,根据正弦定理、余弦定理或相似三角形等数学知识可求得未知力
02
合成法与分解法
例1:如图所示,一个半球形的碗放在桌面上,碗口水平,O点为其球心,碗的内表面及碗口是光滑的。一根细线跨在碗口上,线的两端分别系有质量为m1和m2的小球,当它们处于平衡状态时,质量为m1的小球与O点的连线与水平面的夹角α=60°,则两小球的质量之比
为( )
A.
B.
C.
D.
02
合成法与分解法
例1:如图所示,一个半球形的碗放在桌面上,碗口水平,O点为其球心,碗的内表面及碗口是光滑的。一根细线跨在碗口上,线的两端分别系有质量为m1和m2的小球,当它们处于平衡状态时,质量为m1的小球与O点的连线与水平面的夹角α=60°,则两小球的质量之比
为( )
A.
B.
C.
D.
A
02
合成法与分解法
巩固练习1:如图甲所示,水平地面上固定一倾角为30°的表面粗糙的斜劈,一质量为m的小物块能沿着斜劈的表面匀速下滑。现对小物块施加一水平向右的恒力F,使它沿该斜劈表面匀速上滑。如图乙所示,则F大小应为( )
A
03
动态平衡问题
1.动态平衡:通过控制某些物理量,使物体的状态发生缓慢的变化,而在这个过程中物体又始终处于一系列的平衡状态,在问题的描述中常用“缓慢”等语言叙述。
2.处理动态平衡问题的一般思路
(1)平行四边形定则是基本方法,但也要根据实际情况采用不同的方法,若出现直角三角形,常用三角函数表示合力与分力的关系。
(2)图解法的适用情况
图解法分析物体动态平衡问题时,一般物体只受三个力作用.
03
动态平衡问题
3.几种常见情况
①一力不变,一力方向不变的三力动态平衡
②一力不变,两力方向都变的三力动态平衡
③一力不变,另两力夹角保持不变的三力动态平衡
03
一力不变,一力方向不变的三力动态平衡
例2:光滑斜面上安装一光滑挡板AO,挡板可绕O处铰链无摩擦转动,在挡板与斜面间放一匀质球,现使挡板从图示位置缓慢转到竖直位置,此过程中球对挡板的压力N1和球对斜面的压力N2的变化情况?
解析:在缓慢转动过程中,选位置1、2、3,可直观判断N1先减小,后增大;N2一直在增大。
巩固练习2:半圆柱体P放在粗糙的水平地面上,其右端有一固定放置的竖直挡板MN。在半圆柱体P和MN之间放有一个光滑均匀的小圆柱体Q,整个装置处于静止。如图所示是这个装置的纵截面图。若用外力先使MN保持竖直,然后缓慢地水平向右移动,在Q落到地面以前,发现P始终保持静止。在此过程中,下列说法正确的是( )
03
一力不变,一力方向不变的三力动态平衡
A.MN对Q的弹力逐渐增大
B.Q所受的合力逐渐增大
C.P、Q间的弹力先减小后增大
D.地面对P的摩擦力逐渐减小
A.MN对Q的弹力逐渐增大
B.Q所受的合力逐渐增大
C.P、Q间的弹力先减小后增大
D.地面对P的摩擦力逐渐减小
巩固练习2:半圆柱体P放在粗糙的水平地面上,其右端有一固定放置的竖直挡板MN。在半圆柱体P和MN之间放有一个光滑均匀的小圆柱体Q,整个装置处于静止。如图所示是这个装置的纵截面图。若用外力先使MN保持竖直,然后缓慢地水平向右移动,在Q落到地面以前,发现P始终保持静止。在此过程中,下列说法正确的是( )
03
一力不变,一力方向不变的三力动态平衡
A.MN对Q的弹力逐渐增大
B.Q所受的合力逐渐增大
C.P、Q间的弹力先减小后增大
D.地面对P的摩擦力逐渐减小
A
03
一力不变,两力方向都变的三力动态平衡
例3:如图所示为一简易起重装置,AC是上端带有滑轮的固定支架,BC为质量不计的轻杆,杆的一端C用较链固定在支架上,另一端B悬挂一个质量为m的重物,并用钢丝绳跨过滑轮A连接在卷扬机上.开始时,杆BC与AC的夹角∠BCA>90°,现使∠BCA缓缓变小,直到∠BCA=30°.在此过程中,杆BC所受的力及钢丝绳的拉力的变化情况(不计一切摩擦阻力)?
解析:受力分析,构建矢量三角形,与△ABC相似,对应边成比例,可得,由于比值恒定且G不变,∠BCA
变小过程中,AC边、BC边不变,AB边变小,可得杆的支持力不变,绳的拉力变小。
巩固练习3:如图所示,质量均为m的小球A、B用劲度系数为k1的轻弹簧相连,B球用长为L的细绳悬于O点,A球固定在O点正下方,当小球B平衡时,绳子所受的拉力为T1,弹簧的弹力为F1;现把A、B间的弹簧换成原长相同但劲度系数为k2(k2>k1)的另一轻弹簧,在其他条件不变的情况下仍使系统平衡,此时绳子所受的拉力为T2,弹簧的弹力为F2,则下列关于T1与T2、F1与F2之间的大小关系正确的是( )
03
一力不变,两力方向都变的三力动态平衡
A.T1>T2
B.T1=T2
C.F1
由三角形相似得
巩固练习3:如图所示,质量均为m的小球A、B用劲度系数为k1的轻弹簧相连,B球用长为L的细绳悬于O点,A球固定在O点正下方,当小球B平衡时,绳子所受的拉力为T1,弹簧的弹力为F1;现把A、B间的弹簧换成原长相同但劲度系数为k2(k2>k1)的另一轻弹簧,在其他条件不变的情况下仍使系统平衡,此时绳子所受的拉力为T2,弹簧的弹力为F2,则下列关于T1与T2、F1与F2之间的大小关系正确的是( )
03
一力不变,两力方向都变的三力动态平衡
A.T1>T2
B.T1=T2
C.F1
BC
03
一力不变,另两力夹角保持不变的三力动态平衡
例3:【2017·全国新课标Ⅰ卷】如图,柔软轻绳ON的一端O固定,其中间某点M拴一重物,用手拉住绳的另一端N。初始时,OM竖直且MN被拉直,OM与MN之间的夹角为
(
)。现将重物向右上方缓慢拉起,并保持夹角
不变。在OM由竖直被拉到水平的过程中(
)
A.MN上的张力逐渐增大
B.MN上的张力先增大后减小
C.OM上的张力逐渐增大
D.OM上的张力先增大后减小
法一:解析法(正弦定理)
矢量三角形中,分别设角θ、β、γ,根据正弦定理有,由题意可知,γ=180°-
α不变,β先增大后减小,θ逐渐增大,故当β=90°时,OM上的张力最大,MN上的张力逐渐增大。
法二:作图法(矢量三角形)
三力合力为零,能构成封闭的三角形,
再借助圆,同一圆弧对应圆周角(γ=180°-α)不变。
P点沿圆弧顺时针方向旋转的过程中,当FOM过直径时最大,而FMN一直增大。
法三:转换法(等效法)
等效细绳OM、MN不动,重力G逆时针旋转90°,同样利用作图法能够判断出OM上的张力先增大后减小,而MN上张力一直增大。
?
03
一力不变,另两力夹角保持不变的三力动态平衡
例3:【2017·全国新课标Ⅰ卷】如图,柔软轻绳ON的一端O固定,其中间某点M拴一重物,用手拉住绳的另一端N。初始时,OM竖直且MN被拉直,OM与MN之间的夹角为
(
)。现将重物向右上方缓慢拉起,并保持夹角
不变。在OM由竖直被拉到水平的过程中(
)
A.MN上的张力逐渐增大
B.MN上的张力先增大后减小
C.OM上的张力逐渐增大
D.OM上的张力先增大后减小
AD
04
临界和极值问题
1.临界问题
当某物理量变化时,会引起其他几个物理量的变化,从而使物体所处的平衡状态“恰好出现”或“恰好不出现”,在问题描述中常用“刚好”“刚能”“恰好”等语言叙述。
2.极值问题
平衡物体的极值,一般是指在力的变化过程中的最大值和最小值问题。
04
临界和极值问题
3.解题思路
解决共点力平衡中的临界、极值问题“四字诀”
例4:将两个质量均为m的小球a、b用细线相连后,再用细线悬挂于O点,如图所示。用力F拉小球b,使两个小球都处于静止状态,且细线Oa与竖直方向的夹角保持θ=30°,则F达到最小值时Oa绳上的拉力为( )
04
临界和极值问题
整体为研究对象,分析受力,作出F在三个方向时整体的受力图,根据平衡条件得知:F与T的合力与重力mg总是大小相等、方向相反,由力的合成图可知,当F与绳子Oa垂直时,F有最小值,即图中2位置,F有最小值,根据平衡条件得F=2mgsin30°=mg,T=2mgcos30°=
mg。
例4:将两个质量均为m的小球a、b用细线相连后,再用细线悬挂于O点,如图所示。用力F拉小球b,使两个小球都处于静止状态,且细线Oa与竖直方向的夹角保持θ=30°,则F达到最小值时Oa绳上的拉力为( )
04
临界和极值问题
A
直击高考
直击高考练习
【2016·全国新课标Ⅱ卷】质量为m的物体用轻绳AB悬挂于天花板上。用水平向左的力F缓慢拉动绳的中点O,如图所示。用T
表示绳OA段拉力的大小,在O点向左移动的过程中(
)
A.F逐渐变大,T逐渐变大
B.F逐渐变大,T逐渐变小
C.F逐渐变小,T逐渐变大
D.F逐渐变小,T逐渐变小
直击高考:
A
【2017·新课标Ⅱ卷】如图,一物块在水平拉力F的作用下沿水平桌面做匀速直线运动。若保持F的大小不变,而方向与水平面成60°角,物块也恰好做匀速直线运动。物块与桌面间的动摩擦因数为(
)
直击高考:
C
感谢观看
THANK
YOU
FOR
WATCHING
