5.3.3分式的加减法(3) 课件(共24张PPT)
文档属性
| 名称 | 5.3.3分式的加减法(3) 课件(共24张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 899.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-27 19:45:23 | ||
图片预览








文档简介
5.3.3分式的加减法(3)
第五章 分式与分式方程
2020-2021北师大版八年级数学下册
学习目标
1、会进行分母是多项式的异分母分式的加减法运算及分式与整式的加减法运算;
2、能进行分式的混合运算及较复杂的分式化简求值;(重点)
3、会运用分式解决实际问题.(难点)
1.异分母分式的加减法法则:
异分母的分式相加减,先通分,化为同分母的分式,然后再按同分母分式的加减法法则进行计算.
★关键:确定最简公分母
导入新课
(3)单一字母(多项式):
确定最简公分母的方法:
(1)确定系数:
(2)相同字母(多项式):
各分母系数的最小公倍数
取最高次幂
连同它的指数一起当作最简公分母的因式
2.确定下列分式的最简公分母
导入新课
异分母分式的加减
解:原式
分母是多项式先因式分解
最简公因式x(y+1)(y-1)
例 计算:
再正确通分,转化为同分母的分式相加减.
探究新知
解:原式
例 计算:
把整式看成分母为“1”的分式
填括号法则,括号前为负号,括号各项都变号
探究新知
解:原式
例 计算:
多个分式相加减通分原理相同
探究新知
知识要点
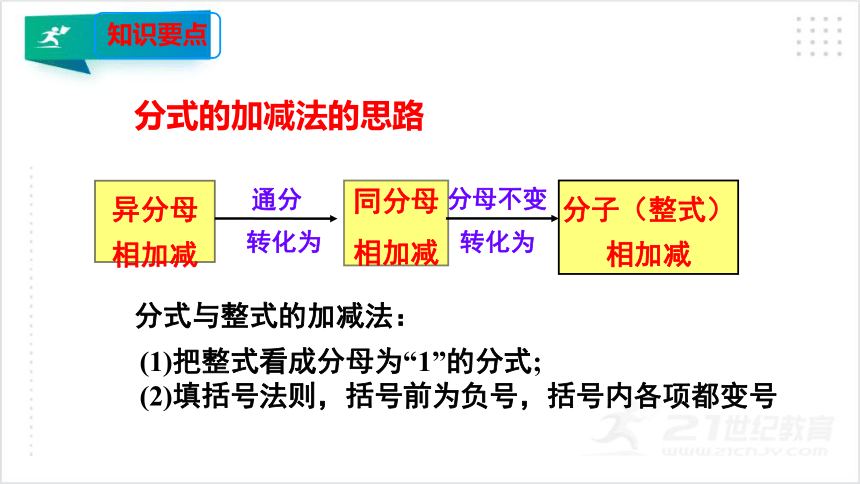
分式的加减法的思路
通分
转化为
异分母相加减
同分母
相加减
分子(整式)相加减
分母不变
转化为
分式与整式的加减法:
(1)把整式看成分母为“1”的分式;
(2)填括号法则,括号前为负号,括号内各项都变号
阅读下面题目的计算过程.
①
= ②
= ③
= ④
(1)上述计算过程,从哪一步开始错误,请写出该步的代号_______;
(2)错误原因___________;
(3)本题的正确结果为: .
②
漏掉了分母
做一做
探究新知
分式的混合运算
问题:如何计算 ?
请先思考这道题包含的运算,确定运算顺序,再独立完成.
探究新知
解:
先乘方,再乘除,最后加减
探究新知
分式的混合运算顺序
先算乘方,再算乘除,最后算加减,有括号的先算括号里面的.
要点归纳
计算结果要化为最简分式或整式.
例 计算:
解:原式
先算括号里的加法,再算括号外的乘法
注:当式子中出现整式时,把整式看成整体,并把分母看做“1”
或
例题讲解
解:原式
注意:分子或分母是多项式的先因式分解,不能分解的要视为整体.
例题讲解
解:原式
方法总结:观察题目的结构特点,灵活运用运算律,适当运用计算技巧,可简化运算,提高速度.
例 计算:
利用乘法分配率简化运算
例题讲解
分式的混合运算
(1)进行混合运算时,要注意运算顺序,在没有括号的情况下,按从左往右的方向,先算乘方,再算乘除,后算加减;
(2)分式的混合运算,一般按常规运算顺序,但有时应先根据题目的特点,运用乘法的运算律进行灵活运算.
混合运算的特点:是整式运算、因式分解、分式运算的综合运用,综合性强.
总结归纳
A. B. C.-1 D.2
1. 计算
的结果为( )
C
2.填空:
4
课堂练习
3.计算:
解:(1)原式=
(2)原式=
课堂练习
课堂练习
4.先化简,再求值: ,其中 .
解:
课堂练习
5.先化简,再求值:: ,其中x=2016.
课堂练习
课堂小结
2.分式的混合运算法则
先算乘除,再算加减;如果有括号先算括号内的.
1.分式加减运算的方法思路:
通分
转化为
异分母相加减
同分母相加减
分子(整式)相加减
分母不变
转化为
https://www.21cnjy.com/help/help_extract.php
第五章 分式与分式方程
2020-2021北师大版八年级数学下册
学习目标
1、会进行分母是多项式的异分母分式的加减法运算及分式与整式的加减法运算;
2、能进行分式的混合运算及较复杂的分式化简求值;(重点)
3、会运用分式解决实际问题.(难点)
1.异分母分式的加减法法则:
异分母的分式相加减,先通分,化为同分母的分式,然后再按同分母分式的加减法法则进行计算.
★关键:确定最简公分母
导入新课
(3)单一字母(多项式):
确定最简公分母的方法:
(1)确定系数:
(2)相同字母(多项式):
各分母系数的最小公倍数
取最高次幂
连同它的指数一起当作最简公分母的因式
2.确定下列分式的最简公分母
导入新课
异分母分式的加减
解:原式
分母是多项式先因式分解
最简公因式x(y+1)(y-1)
例 计算:
再正确通分,转化为同分母的分式相加减.
探究新知
解:原式
例 计算:
把整式看成分母为“1”的分式
填括号法则,括号前为负号,括号各项都变号
探究新知
解:原式
例 计算:
多个分式相加减通分原理相同
探究新知
知识要点
分式的加减法的思路
通分
转化为
异分母相加减
同分母
相加减
分子(整式)相加减
分母不变
转化为
分式与整式的加减法:
(1)把整式看成分母为“1”的分式;
(2)填括号法则,括号前为负号,括号内各项都变号
阅读下面题目的计算过程.
①
= ②
= ③
= ④
(1)上述计算过程,从哪一步开始错误,请写出该步的代号_______;
(2)错误原因___________;
(3)本题的正确结果为: .
②
漏掉了分母
做一做
探究新知
分式的混合运算
问题:如何计算 ?
请先思考这道题包含的运算,确定运算顺序,再独立完成.
探究新知
解:
先乘方,再乘除,最后加减
探究新知
分式的混合运算顺序
先算乘方,再算乘除,最后算加减,有括号的先算括号里面的.
要点归纳
计算结果要化为最简分式或整式.
例 计算:
解:原式
先算括号里的加法,再算括号外的乘法
注:当式子中出现整式时,把整式看成整体,并把分母看做“1”
或
例题讲解
解:原式
注意:分子或分母是多项式的先因式分解,不能分解的要视为整体.
例题讲解
解:原式
方法总结:观察题目的结构特点,灵活运用运算律,适当运用计算技巧,可简化运算,提高速度.
例 计算:
利用乘法分配率简化运算
例题讲解
分式的混合运算
(1)进行混合运算时,要注意运算顺序,在没有括号的情况下,按从左往右的方向,先算乘方,再算乘除,后算加减;
(2)分式的混合运算,一般按常规运算顺序,但有时应先根据题目的特点,运用乘法的运算律进行灵活运算.
混合运算的特点:是整式运算、因式分解、分式运算的综合运用,综合性强.
总结归纳
A. B. C.-1 D.2
1. 计算
的结果为( )
C
2.填空:
4
课堂练习
3.计算:
解:(1)原式=
(2)原式=
课堂练习
课堂练习
4.先化简,再求值: ,其中 .
解:
课堂练习
5.先化简,再求值:: ,其中x=2016.
课堂练习
课堂小结
2.分式的混合运算法则
先算乘除,再算加减;如果有括号先算括号内的.
1.分式加减运算的方法思路:
通分
转化为
异分母相加减
同分母相加减
分子(整式)相加减
分母不变
转化为
https://www.21cnjy.com/help/help_extract.php
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
