2020-2021学年人教五四新版八年级下册数学期末练习试题(Word版有答案)
文档属性
| 名称 | 2020-2021学年人教五四新版八年级下册数学期末练习试题(Word版有答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 474.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(五四学制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-28 00:00:00 | ||
图片预览


文档简介
2020-2021学年人教五四新版八年级下册数学期末练习试题
一.选择题
1.下列解析式中,y不是x的函数的是( )
A.y=2x
B.y=x2
C.y=±(x>0)
D.y=|x|
2.下列计算正确的是( )
A.
B.
C.
D.
3.下列各组数中,不能构成直角三角形的是( )
A.a=1,b=,c=
B.a=5,b=12,c=13
C.a=1,b=3,c=
D.a=1,b=1,c=2
4.矩形具有而平行四边形不一定具有的性质是( )
A.对边相等
B.对角相等
C.对角线相等
D.对角线互相平分
5.若一次函数y=kx+b的图象经过一、二、四象限,则一次函数y=﹣bx+k的图象不经过( )
A.第一象限
B.第二象限
C.第三象限
D.第四象限
6.高为3,底边长为8的等腰三角形腰长为( )
A.3
B.4
C.5
D.6
7.等腰三角形的底边长为10cm,一腰上的中线把三角形周长分成两部分的差为4cm,则这个三角形的腰长是( )
A.6cm
B.14cm
C.4cm或14cm
D.6cm或14cm
8.如图,在Rt△ABC中,∠ABC=90°,AB=8,BC=6,D是AC的中点,AF平分∠BAC交BD于点E,则BE的长为( )
A.
B.3
C.
D.
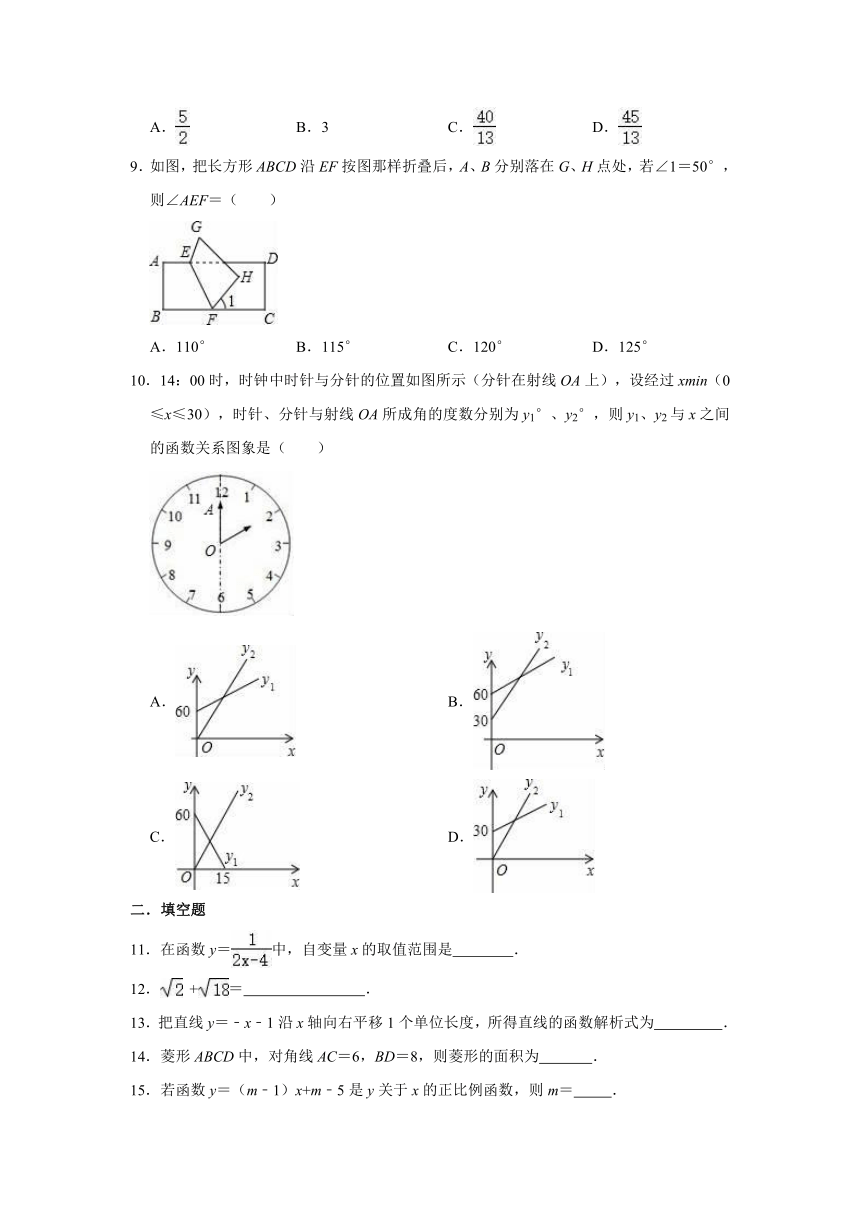
9.如图,把长方形ABCD沿EF按图那样折叠后,A、B分别落在G、H点处,若∠1=50°,则∠AEF=( )
A.110°
B.115°
C.120°
D.125°
10.14:00时,时钟中时针与分针的位置如图所示(分针在射线OA上),设经过xmin(0≤x≤30),时针、分针与射线OA所成角的度数分别为y1°、y2°,则y1、y2与x之间的函数关系图象是( )
A.
B.
C.
D.
二.填空题
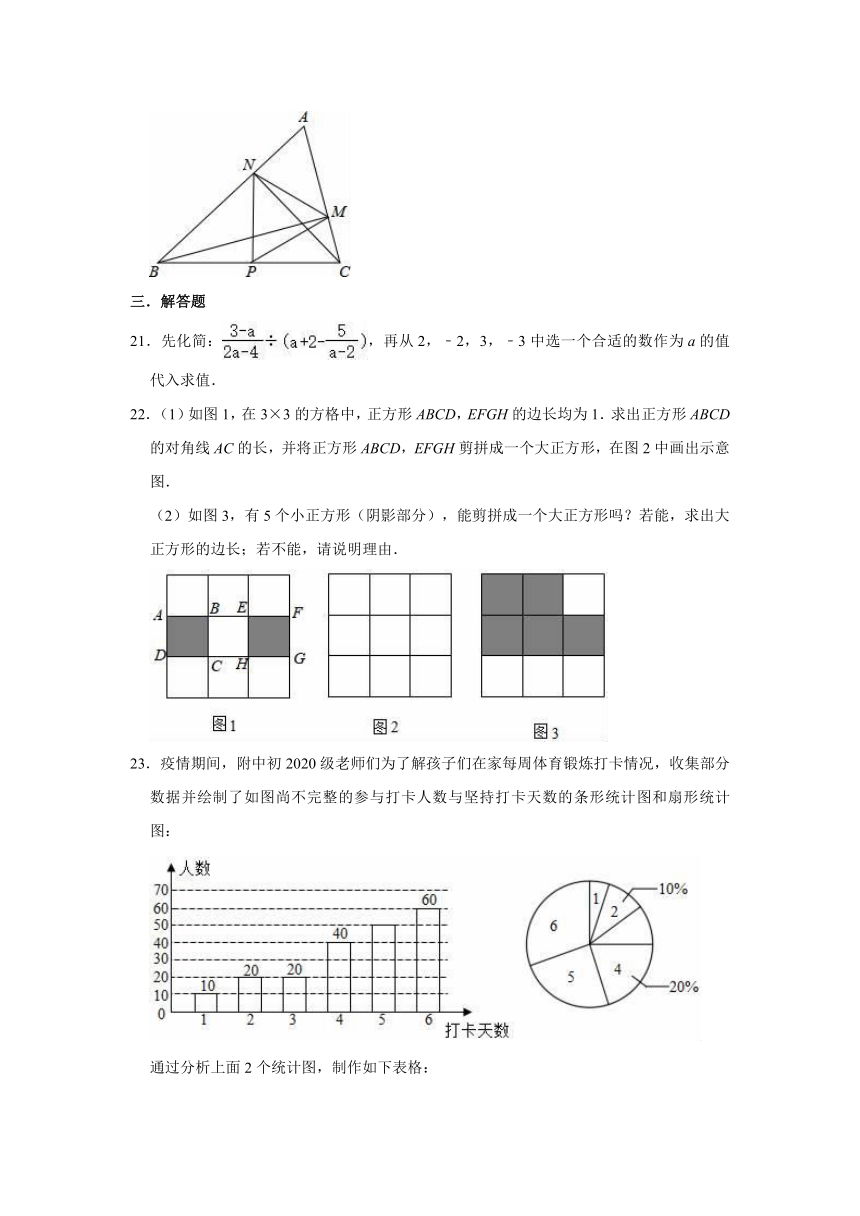
11.在函数y=中,自变量x的取值范围是
.
12.
+=
.
13.把直线y=﹣x﹣1沿x轴向右平移1个单位长度,所得直线的函数解析式为
.
14.菱形ABCD中,对角线AC=6,BD=8,则菱形的面积为
.
15.若函数y=(m﹣1)x+m﹣5是y关于x的正比例函数,则m=
.
16.如图,矩形ABCD中,AB=6,BC=8,点E是BC边上一点,连接AE,把△ABE沿AE折叠,使点B落在点F处,当△CEF为直角三角形时,CF的长为
.
17.如图,在?ABCD中,按以下步骤作图:①以点A为圆心,AB的长为半径作弧,交AD于点F;②分别以点B、F为圆心,大于BF的长为半径作弧,两弧在∠BAD内交于点G;③作射线AG,交边BC于点E.若BF=6,AB=5,则AE的长是
.
18.如图,已知正方形ABCD中,两动点M和N分别从顶点B、C同时出发,以相同的速度沿BC、CD向终点C、D运动,连接AM、BN,交于点P,再连接PC,若AB=4,则PC长的最小值为
.
19.如图,在Rt△ABC中,∠A=90°,AB=6,BC=10,P是BC边上的一点,作PE垂直AB,PF垂直AC,垂足分别为E、F,求EF的最小值是
.
20.△ABC中,∠A=60°,BM⊥AC于点M,CN⊥AB于点N,P为BC边的中点,连接PM,PN,则下列结论:①PM=PN②③△PMN为等边三角形
④若BN=CP,则∠ACB=75°.则正确结论是
.
三.解答题
21.先化简:,再从2,﹣2,3,﹣3中选一个合适的数作为a的值代入求值.
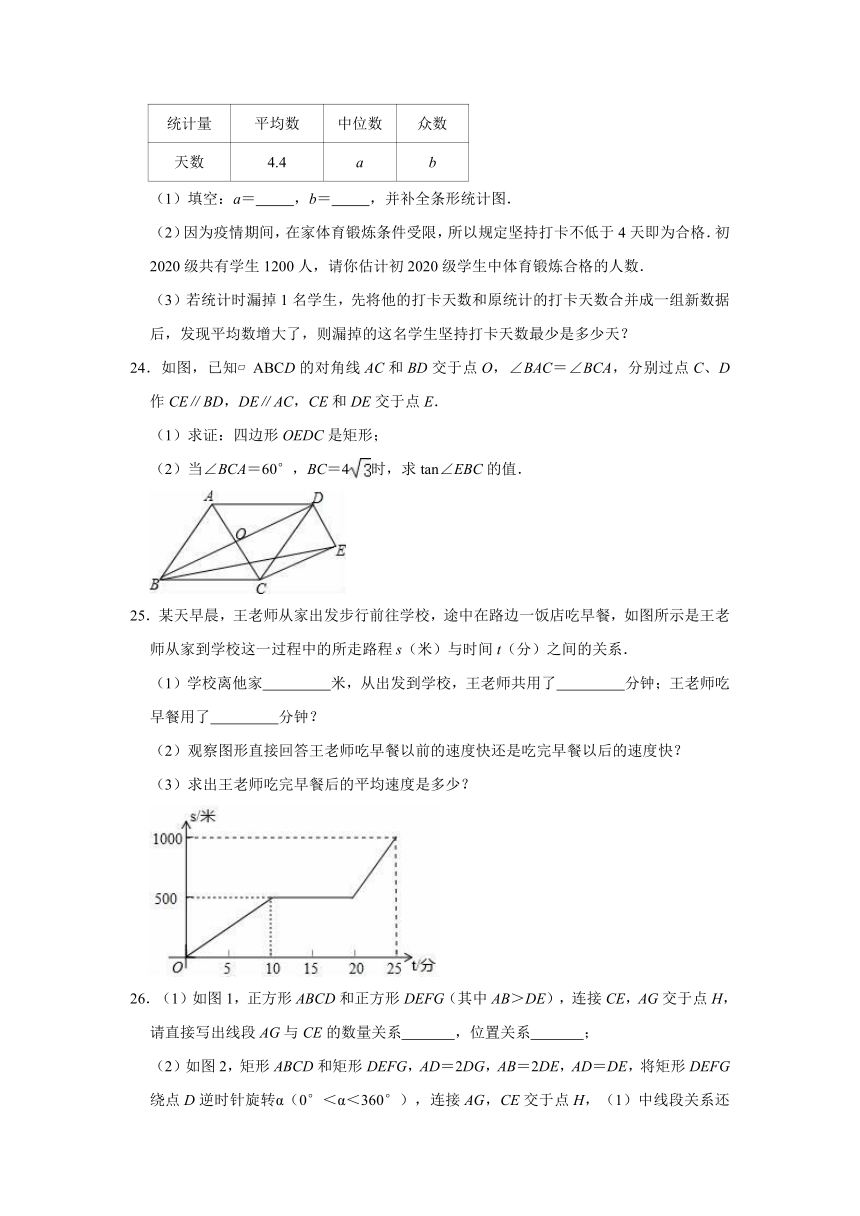
22.(1)如图1,在3×3的方格中,正方形ABCD,EFGH的边长均为1.求出正方形ABCD的对角线AC的长,并将正方形ABCD,EFGH剪拼成一个大正方形,在图2中画出示意图.
(2)如图3,有5个小正方形(阴影部分),能剪拼成一个大正方形吗?若能,求出大正方形的边长;若不能,请说明理由.
23.疫情期间,附中初2020级老师们为了解孩子们在家每周体育锻炼打卡情况,收集部分数据并绘制了如图尚不完整的参与打卡人数与坚持打卡天数的条形统计图和扇形统计图:
通过分析上面2个统计图,制作如下表格:
统计量
平均数
中位数
众数
天数
4.4
a
b
(1)填空:a=
,b=
,并补全条形统计图.
(2)因为疫情期间,在家体育锻炼条件受限,所以规定坚持打卡不低于4天即为合格.初2020级共有学生1200人,请你估计初2020级学生中体育锻炼合格的人数.
(3)若统计时漏掉1名学生,先将他的打卡天数和原统计的打卡天数合并成一组新数据后,发现平均数增大了,则漏掉的这名学生坚持打卡天数最少是多少天?
24.如图,已知?ABCD的对角线AC和BD交于点O,∠BAC=∠BCA,分别过点C、D作CE∥BD,DE∥AC,CE和DE交于点E.
(1)求证:四边形OEDC是矩形;
(2)当∠BCA=60°,BC=4时,求tan∠EBC的值.
25.某天早晨,王老师从家出发步行前往学校,途中在路边一饭店吃早餐,如图所示是王老师从家到学校这一过程中的所走路程s(米)与时间t(分)之间的关系.
(1)学校离他家
米,从出发到学校,王老师共用了
分钟;王老师吃早餐用了
分钟?
(2)观察图形直接回答王老师吃早餐以前的速度快还是吃完早餐以后的速度快?
(3)求出王老师吃完早餐后的平均速度是多少?
26.(1)如图1,正方形ABCD和正方形DEFG(其中AB>DE),连接CE,AG交于点H,请直接写出线段AG与CE的数量关系
,位置关系
;
(2)如图2,矩形ABCD和矩形DEFG,AD=2DG,AB=2DE,AD=DE,将矩形DEFG绕点D逆时针旋转α(0°<α<360°),连接AG,CE交于点H,(1)中线段关系还成立吗?若成立,请写出理由;若不成立,请写出线段AG,CE的数量关系和位置关系,并说明理由;
(3)矩形ABCD和矩形DEFG,AD=2DG=6,AB=2DE=8,将矩形DEFG绕点D逆时针旋转α(0°<α<360°),直线AG,CE交于点H,当点E与点H重合时,请直接写出线段AE的长.
27.如图,在平面直角坐标系中,过点C(0,6)的直线AC与直线OA相交于点A(4,2).
(1)求直线AC的表达式;
(2)求△OAC的面积;
(3)动点M在线段OA和射线AC上运动,是否存在点M,使△OMC的面积是△OAC的面积的?若存在,求出此时点M的坐标;若不存在,请说明理由.
参考答案与试题解析
一.选择题
1.解:A、y=2x对于x的每一个取值,y都有唯一确定的值,符合函数的定义;
B、y=x2对于x的每一个取值,y都有唯一确定的值,符合函数的定义;
C、y=±(x>0)对于x的每一个取值,y有两个确定的值,不符合函数的定义;
D、y=|x|对于x的每一个取值,y都有唯一确定的值,符合函数的定义.
故选:C.
2.解:(B)原式==,故B错误;
(C)原式=﹣,故C错误;
(D)原式=|2﹣|=﹣2,故D错误;
故选:A.
3.解:A、12+()2=()2,此三角形是直角三角形,故本选项不符合题意;
B、52+122=132,此三角形是直角三角形,故本选项不符合题意;
C、12+32=()2,此三角形是直角三角形,故本选项不符合题意;
D、12+12≠22,此三角形不是直角三角形,故本选项符合题意;
故选:D.
4.解:矩形的对角线相等,而平行四边形的对角线不一定相等.
故选:C.
5.解:一次函数y=kx+b过一、二、四象限,
则函数值y随x的增大而减小,因而k<0;
图象与y轴的正半轴相交则b>0,
因此一次函数y=﹣bx+k的一次项系数﹣b<0,
y随x的增大而减小,经过二四象限,
常数项k<0,则函数与y轴负半轴相交,
因此一定经过二三四象限,
因此函数不经过第一象限.
故选:A.
6.解:∵AD⊥BC,
∴BD=CD,
∵BC=8,
∴BD=4,
又AD=3,
在Rt△ABD中,AB==5.
故选:C.
7.解:如图,
BC=10,由题意一腰上的中线把三角形周长分成两部分的差为4
cm
所以AC+AD﹣BD﹣BC=4,即AC=14cm
也有可能是BD+BC﹣AC﹣AD=4,解得AC=6cm
故选:D.
8.解:过点F作FG⊥AC于G,作DH∥AF交BC于H,
在Rt△ABC中,∠ABC=90°,AB=8,BC=6,D是AC的中点,
∴BD=AC,AC==10,
∴BD=5,
∵AF平分∠BAC,FG⊥AC,∠ABC=90°,
∴BF=FG,
∵∠C=∠C,∠CGF=∠CBA=90°,
∴△CGF∽△CBA,
∴,即,
∴BF=,
∴CF=BC﹣BF=,
∵D是AC的中点,DH∥AF,
∴DH是△AFC的中位线,
∴FH=CF=,
∴BH=BF+FH=,
∵DH∥AF,
∴△BEF∽△BDH,
∴,即,
∴BE=.
故选:C.
9.解:如图,
∵四边形ABCD为长方形,
∴AE∥BF,∠AEF+∠BFE=180°;
由折叠变换的性质得:
∠BFE=∠HFE,而∠1=50°,
∴∠BFE=(180°﹣50°)÷2=65°,
∴∠AEF=180°﹣65°=115°.
故选:B.
10.解:由题意,得
y1=0.5x+60(0≤x≤30),
y2=6x(0≤x≤30),
∴得出y1是一次函数,y1随x的增大而僧大,与y轴的交点是(0,60),y2是正比例函数,y2随x的增大而增大,
∴A答案正确,故选:A.
二.填空题
11.解:根据题意得2x﹣4≠0,
解得x≠2;
∴自变量x的取值范围是x≠2.
12.解:原式=+3
=4.
故答案为:4.
13.解:把直线y=﹣x﹣1沿x轴向右平移1个单位长度,所得直线的函数解析式为:y=﹣(x﹣1)﹣1=﹣x.
故答案为:y=﹣x.
14.解:菱形的面积计算公式S=ab(a、b为菱形对角线长)
故菱形的面积为S=ab=×6×8=24.
故答案为:24.
15.解:由题意得:m﹣5=0,且m﹣1≠0,
解得:m=5,
故答案为:5.
16.解:当△CEF为直角三角形时,有两种情况:
①当点F落在矩形内部时,如答图1所示.
连接AC,
在Rt△ABC中,AB=6,BC=8,
∴AC=10,
∵∠B沿AE折叠,使点B落在点F处,
∴∠AFE=∠B=90°,
当△CEF为直角三角形时,只能得到∠EFC=90°,
∴点A、F、C共线,即∠B沿AE折叠,使点B落在对角线AC上的点F处,
∴EB=EF,AB=AF=6,
∴CF=10﹣6=4;
②当点F落在AD边上时,如答图2所示.
此时ABEF为正方形,
∴BE=AB=6,CE=8﹣6=2,
∴CF=2.
综上所述,CF的长为4或2.
故答案为:4或2.
17.解:如图,设AE交BF于点O.
由作图可知:AB=AF,AE⊥BF,
∴OB=OF,∠BAE=∠EAF,
∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠EAF=∠AEB,
∴∠BAE=∠AEB,
∴AB=BE=AF,∵AF∥BE,
∴四边形ABEF是平行四边形,
∵AB=AF,
∴四边形ABEF是菱形,
∴OA=OE,OB=OF=3,
在Rt△AOB中,∵∠AOB=90°,
∴OA===4,
∴AE=2OA=8.
故答案为8.
18.解:由题意得:BM=CN,
∵四边形ABCD是正方形,
∴∠ABM=∠BCN=90°,AB=BC=4,
在△ABM和△BCN中,
,
∴△ABM≌△BCN(SAS),
∴∠BAM=∠CBN,
∵∠ABP+∠CBN=90°,
∴∠ABP+∠BAM=90°,
∴∠APB=90°,
∴点P在以AB为直径的圆上运动,设圆心为O,运动路径一条弧,是这个圆的,如图所示:
连接OC交圆O于P,此时PC最小,
∵AB=4,
∴OP=OB=2,
由勾股定理得:OC==2,
∴PC=OC﹣OP=2﹣2;
故答案为:2﹣2.
19.解:连接AP,
∵∠BAC=90°,PE⊥AB,PF⊥AC,
∴∠BAC=∠AEP=∠AFP=90°,
∴四边形AFPE是矩形,
∴EF=AP,
要使EF最小,只要AP最小即可,
当AP⊥BC时,AP最小,
在Rt△BAC中,∠BAC=90°,AB=6,BC=10,
由勾股定理得:AC===8,
由三角形面积公式得:△ABC的面积=×AB×AC=×BC×AP,
∴AP===4.8,
即EF=4.8,
故答案为:4.8.
20.解:①∵BM⊥AC于点M,CN⊥AB于点N,P为BC边的中点,
∴PM=BC,PN=BC,
∴PM=PN,故①正确;
②在△ABM与△ACN中,
∵∠A=∠A,∠AMB=∠ANC=90°,
∴△ABM∽△ACN,
∴=,
∴=,故②正确;
③∵∠A=60°,BM⊥AC于点M,CN⊥AB于点N,
∴∠ABM=∠ACN=30°,
在△ABC中,∠BCN+∠CBM=180°﹣60°﹣30°×2=60°,
∵点P是BC的中点,BM⊥AC,CN⊥AB,
∴PM=PN=PB=PC,
∴∠BPN=2∠BCN,∠CPM=2∠CBM,
∴∠BPN+∠CPM=2(∠BCN+∠CBM)=2×60°=120°,
∴∠MPN=60°,
∴△PMN是等边三角形,故③正确;
∵BN=CP,BP=CP(P为BC的中点),
∴BN=BP,
∵∠BPN=90°,
∴∠ABC=45°,
∵∠A=60°,
∴∠ACB=180°﹣∠A﹣∠ABC=75°,故④正确;
故答案为:①②③④.
三.解答题
21.解:原式=÷(﹣)
=?
=﹣,
∵a﹣2≠0,a﹣3≠0,a+3≠0,
∴a≠2,a≠±3,
∴当a=﹣2时,原式=﹣=﹣.
22.解:(1)如图2中,正方形PQMN即为所求作.
(2)能,拼成正方形,边长为,如图3所示.
23.解:(1)本次调查的人数为:20÷10%=200,
打卡5天的学生有:200﹣10﹣20﹣20﹣40﹣60=50(人),
故a=5,b=6,
补全的条形统计图如右图所示,
故答案为:5,6;
(2)1200×=900(人),
即初2020级学生中体育锻炼合格的有900人;
(3)由题意可得,
漏掉的这名学生坚持打卡天数最少是5天.
24.(1)证明:∵四边形ABCD是平行四边形,
∴AB=CD,AD=BC,
∵∠BAC=∠BCA,
∴AB=BC,
∴AB=CD=AD=BC,
∴四边形ABCD是菱形,
∴AC⊥BD,
∴∠DOC=90°,
∵CE∥BD,
∴∠OCE=90°,
同理可得∠ODE=90°,
∴四边形OEDC是矩形;
(2)解:过点E作EF垂直BC交BC延长线于点F,
∵∠BCA=60°,
∴∠BCD=120°,
∴∠ECF=120°﹣90°=30°,
∵BC=4,
∴BO=OD=6,
∴OD=CE=6,
∴EF=3,CF=3,
∴tan∠EBC==.
25.解:(1)学校离他家1000米,从出发到学校,王老师共用了25分钟;王老师吃早餐用了20﹣10=10分钟
故答案为:1000,25,10;
(2)根据图象可得:,所以吃完早餐以后速度快;
(3)(1000﹣500)÷(25﹣20)=100(米/分)
答:吃完早餐后的平均速度是100米/分.
26.解:(1)如图1,
在正方形ABCD和正方形DEFG中,∠ADC=∠EDG=90°,
∴∠ADE+∠EDG=∠ADC+∠ADE,
即∠ADG=∠CDE,
∵DG=DE,DA=DC,
∴△GDA≌△EDC(SAS),
∴AG=CE,∠GAD=∠ECD,
∵∠COD=∠AOH,
∴∠AHO=∠CDO=90°,
∴AG⊥CE,
故答案为:相等,垂直;
(2)不成立,CE=2AG,AG⊥CE,理由如下:
如图2,由(1)知,∠EDC=∠ADG,
∵AD=2DG,AB=2DE,AD=DE,
∴,==,
∴=,
∴△GDA∽△EDC,
∴=,即CE=2AG,
∵△GDA∽△EDC,
∴∠ECD=∠GAD,
∵∠COD=∠AOH,
∴∠AHO=∠CDO=90°,
∴AG⊥CE;
(3)①当点E在线段AG上时,如图3,
在Rt△EGD中,DG=3,ED=4,则EG=5,
过点D作DP⊥AG于点P,
∵∠DPG=∠EDG=90°,∠DGP=∠EGD,
∴△DGP∽△EGD,
∴=,即,
∴PD=,PG=,
则AP===,
则AE=AG﹣GE=AP+GP﹣GE=+﹣5=;
②当点G在线段AE上时,如图4,
过点D作DP⊥AG于点P,
∵∠DPG=∠EDG=90°,∠DGP=∠EGD,
同理得:PD=,AP=,
由勾股定理得:PE==,
则AE=AP+PE=+=;
综上,AE的长为.
27.解:(1)设直线AC的解析式是y=kx+b,
根据题意得:,
解得:.
则直线AC的解析式是:y=﹣x+6;
(2)∵C(0,6),A(4,2),
∴OC=6,
∴S△OAC=×6×4=12;
(3)设OA的解析式是y=mx,则4m=2,
解得:m=.
则直线的解析式是:y=x,
∵当△OMC的面积是△OAC的面积的时,
∴M到y轴的距离是×4=1,
∴点M的横坐标为1或﹣1;
当M的横坐标是:1,
在y=x中,当x=1时,y=,则M的坐标是(1,);
在y=﹣x+6中,x=1则y=5,则M的坐标是(1,5).
则M的坐标是:M1(1,)或M2(1,5).
当M的横坐标是:﹣1,
在y=﹣x+6中,当x=﹣1时,y=7,则M的坐标是(﹣1,7).
综上所述:M的坐标是:M1(1,)或M2(1,5)或M3(﹣1,7).
一.选择题
1.下列解析式中,y不是x的函数的是( )
A.y=2x
B.y=x2
C.y=±(x>0)
D.y=|x|
2.下列计算正确的是( )
A.
B.
C.
D.
3.下列各组数中,不能构成直角三角形的是( )
A.a=1,b=,c=
B.a=5,b=12,c=13
C.a=1,b=3,c=
D.a=1,b=1,c=2
4.矩形具有而平行四边形不一定具有的性质是( )
A.对边相等
B.对角相等
C.对角线相等
D.对角线互相平分
5.若一次函数y=kx+b的图象经过一、二、四象限,则一次函数y=﹣bx+k的图象不经过( )
A.第一象限
B.第二象限
C.第三象限
D.第四象限
6.高为3,底边长为8的等腰三角形腰长为( )
A.3
B.4
C.5
D.6
7.等腰三角形的底边长为10cm,一腰上的中线把三角形周长分成两部分的差为4cm,则这个三角形的腰长是( )
A.6cm
B.14cm
C.4cm或14cm
D.6cm或14cm
8.如图,在Rt△ABC中,∠ABC=90°,AB=8,BC=6,D是AC的中点,AF平分∠BAC交BD于点E,则BE的长为( )
A.
B.3
C.
D.
9.如图,把长方形ABCD沿EF按图那样折叠后,A、B分别落在G、H点处,若∠1=50°,则∠AEF=( )
A.110°
B.115°
C.120°
D.125°
10.14:00时,时钟中时针与分针的位置如图所示(分针在射线OA上),设经过xmin(0≤x≤30),时针、分针与射线OA所成角的度数分别为y1°、y2°,则y1、y2与x之间的函数关系图象是( )
A.
B.
C.
D.
二.填空题
11.在函数y=中,自变量x的取值范围是
.
12.
+=
.
13.把直线y=﹣x﹣1沿x轴向右平移1个单位长度,所得直线的函数解析式为
.
14.菱形ABCD中,对角线AC=6,BD=8,则菱形的面积为
.
15.若函数y=(m﹣1)x+m﹣5是y关于x的正比例函数,则m=
.
16.如图,矩形ABCD中,AB=6,BC=8,点E是BC边上一点,连接AE,把△ABE沿AE折叠,使点B落在点F处,当△CEF为直角三角形时,CF的长为
.
17.如图,在?ABCD中,按以下步骤作图:①以点A为圆心,AB的长为半径作弧,交AD于点F;②分别以点B、F为圆心,大于BF的长为半径作弧,两弧在∠BAD内交于点G;③作射线AG,交边BC于点E.若BF=6,AB=5,则AE的长是
.
18.如图,已知正方形ABCD中,两动点M和N分别从顶点B、C同时出发,以相同的速度沿BC、CD向终点C、D运动,连接AM、BN,交于点P,再连接PC,若AB=4,则PC长的最小值为
.
19.如图,在Rt△ABC中,∠A=90°,AB=6,BC=10,P是BC边上的一点,作PE垂直AB,PF垂直AC,垂足分别为E、F,求EF的最小值是
.
20.△ABC中,∠A=60°,BM⊥AC于点M,CN⊥AB于点N,P为BC边的中点,连接PM,PN,则下列结论:①PM=PN②③△PMN为等边三角形
④若BN=CP,则∠ACB=75°.则正确结论是
.
三.解答题
21.先化简:,再从2,﹣2,3,﹣3中选一个合适的数作为a的值代入求值.
22.(1)如图1,在3×3的方格中,正方形ABCD,EFGH的边长均为1.求出正方形ABCD的对角线AC的长,并将正方形ABCD,EFGH剪拼成一个大正方形,在图2中画出示意图.
(2)如图3,有5个小正方形(阴影部分),能剪拼成一个大正方形吗?若能,求出大正方形的边长;若不能,请说明理由.
23.疫情期间,附中初2020级老师们为了解孩子们在家每周体育锻炼打卡情况,收集部分数据并绘制了如图尚不完整的参与打卡人数与坚持打卡天数的条形统计图和扇形统计图:
通过分析上面2个统计图,制作如下表格:
统计量
平均数
中位数
众数
天数
4.4
a
b
(1)填空:a=
,b=
,并补全条形统计图.
(2)因为疫情期间,在家体育锻炼条件受限,所以规定坚持打卡不低于4天即为合格.初2020级共有学生1200人,请你估计初2020级学生中体育锻炼合格的人数.
(3)若统计时漏掉1名学生,先将他的打卡天数和原统计的打卡天数合并成一组新数据后,发现平均数增大了,则漏掉的这名学生坚持打卡天数最少是多少天?
24.如图,已知?ABCD的对角线AC和BD交于点O,∠BAC=∠BCA,分别过点C、D作CE∥BD,DE∥AC,CE和DE交于点E.
(1)求证:四边形OEDC是矩形;
(2)当∠BCA=60°,BC=4时,求tan∠EBC的值.
25.某天早晨,王老师从家出发步行前往学校,途中在路边一饭店吃早餐,如图所示是王老师从家到学校这一过程中的所走路程s(米)与时间t(分)之间的关系.
(1)学校离他家
米,从出发到学校,王老师共用了
分钟;王老师吃早餐用了
分钟?
(2)观察图形直接回答王老师吃早餐以前的速度快还是吃完早餐以后的速度快?
(3)求出王老师吃完早餐后的平均速度是多少?
26.(1)如图1,正方形ABCD和正方形DEFG(其中AB>DE),连接CE,AG交于点H,请直接写出线段AG与CE的数量关系
,位置关系
;
(2)如图2,矩形ABCD和矩形DEFG,AD=2DG,AB=2DE,AD=DE,将矩形DEFG绕点D逆时针旋转α(0°<α<360°),连接AG,CE交于点H,(1)中线段关系还成立吗?若成立,请写出理由;若不成立,请写出线段AG,CE的数量关系和位置关系,并说明理由;
(3)矩形ABCD和矩形DEFG,AD=2DG=6,AB=2DE=8,将矩形DEFG绕点D逆时针旋转α(0°<α<360°),直线AG,CE交于点H,当点E与点H重合时,请直接写出线段AE的长.
27.如图,在平面直角坐标系中,过点C(0,6)的直线AC与直线OA相交于点A(4,2).
(1)求直线AC的表达式;
(2)求△OAC的面积;
(3)动点M在线段OA和射线AC上运动,是否存在点M,使△OMC的面积是△OAC的面积的?若存在,求出此时点M的坐标;若不存在,请说明理由.
参考答案与试题解析
一.选择题
1.解:A、y=2x对于x的每一个取值,y都有唯一确定的值,符合函数的定义;
B、y=x2对于x的每一个取值,y都有唯一确定的值,符合函数的定义;
C、y=±(x>0)对于x的每一个取值,y有两个确定的值,不符合函数的定义;
D、y=|x|对于x的每一个取值,y都有唯一确定的值,符合函数的定义.
故选:C.
2.解:(B)原式==,故B错误;
(C)原式=﹣,故C错误;
(D)原式=|2﹣|=﹣2,故D错误;
故选:A.
3.解:A、12+()2=()2,此三角形是直角三角形,故本选项不符合题意;
B、52+122=132,此三角形是直角三角形,故本选项不符合题意;
C、12+32=()2,此三角形是直角三角形,故本选项不符合题意;
D、12+12≠22,此三角形不是直角三角形,故本选项符合题意;
故选:D.
4.解:矩形的对角线相等,而平行四边形的对角线不一定相等.
故选:C.
5.解:一次函数y=kx+b过一、二、四象限,
则函数值y随x的增大而减小,因而k<0;
图象与y轴的正半轴相交则b>0,
因此一次函数y=﹣bx+k的一次项系数﹣b<0,
y随x的增大而减小,经过二四象限,
常数项k<0,则函数与y轴负半轴相交,
因此一定经过二三四象限,
因此函数不经过第一象限.
故选:A.
6.解:∵AD⊥BC,
∴BD=CD,
∵BC=8,
∴BD=4,
又AD=3,
在Rt△ABD中,AB==5.
故选:C.
7.解:如图,
BC=10,由题意一腰上的中线把三角形周长分成两部分的差为4
cm
所以AC+AD﹣BD﹣BC=4,即AC=14cm
也有可能是BD+BC﹣AC﹣AD=4,解得AC=6cm
故选:D.
8.解:过点F作FG⊥AC于G,作DH∥AF交BC于H,
在Rt△ABC中,∠ABC=90°,AB=8,BC=6,D是AC的中点,
∴BD=AC,AC==10,
∴BD=5,
∵AF平分∠BAC,FG⊥AC,∠ABC=90°,
∴BF=FG,
∵∠C=∠C,∠CGF=∠CBA=90°,
∴△CGF∽△CBA,
∴,即,
∴BF=,
∴CF=BC﹣BF=,
∵D是AC的中点,DH∥AF,
∴DH是△AFC的中位线,
∴FH=CF=,
∴BH=BF+FH=,
∵DH∥AF,
∴△BEF∽△BDH,
∴,即,
∴BE=.
故选:C.
9.解:如图,
∵四边形ABCD为长方形,
∴AE∥BF,∠AEF+∠BFE=180°;
由折叠变换的性质得:
∠BFE=∠HFE,而∠1=50°,
∴∠BFE=(180°﹣50°)÷2=65°,
∴∠AEF=180°﹣65°=115°.
故选:B.
10.解:由题意,得
y1=0.5x+60(0≤x≤30),
y2=6x(0≤x≤30),
∴得出y1是一次函数,y1随x的增大而僧大,与y轴的交点是(0,60),y2是正比例函数,y2随x的增大而增大,
∴A答案正确,故选:A.
二.填空题
11.解:根据题意得2x﹣4≠0,
解得x≠2;
∴自变量x的取值范围是x≠2.
12.解:原式=+3
=4.
故答案为:4.
13.解:把直线y=﹣x﹣1沿x轴向右平移1个单位长度,所得直线的函数解析式为:y=﹣(x﹣1)﹣1=﹣x.
故答案为:y=﹣x.
14.解:菱形的面积计算公式S=ab(a、b为菱形对角线长)
故菱形的面积为S=ab=×6×8=24.
故答案为:24.
15.解:由题意得:m﹣5=0,且m﹣1≠0,
解得:m=5,
故答案为:5.
16.解:当△CEF为直角三角形时,有两种情况:
①当点F落在矩形内部时,如答图1所示.
连接AC,
在Rt△ABC中,AB=6,BC=8,
∴AC=10,
∵∠B沿AE折叠,使点B落在点F处,
∴∠AFE=∠B=90°,
当△CEF为直角三角形时,只能得到∠EFC=90°,
∴点A、F、C共线,即∠B沿AE折叠,使点B落在对角线AC上的点F处,
∴EB=EF,AB=AF=6,
∴CF=10﹣6=4;
②当点F落在AD边上时,如答图2所示.
此时ABEF为正方形,
∴BE=AB=6,CE=8﹣6=2,
∴CF=2.
综上所述,CF的长为4或2.
故答案为:4或2.
17.解:如图,设AE交BF于点O.
由作图可知:AB=AF,AE⊥BF,
∴OB=OF,∠BAE=∠EAF,
∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠EAF=∠AEB,
∴∠BAE=∠AEB,
∴AB=BE=AF,∵AF∥BE,
∴四边形ABEF是平行四边形,
∵AB=AF,
∴四边形ABEF是菱形,
∴OA=OE,OB=OF=3,
在Rt△AOB中,∵∠AOB=90°,
∴OA===4,
∴AE=2OA=8.
故答案为8.
18.解:由题意得:BM=CN,
∵四边形ABCD是正方形,
∴∠ABM=∠BCN=90°,AB=BC=4,
在△ABM和△BCN中,
,
∴△ABM≌△BCN(SAS),
∴∠BAM=∠CBN,
∵∠ABP+∠CBN=90°,
∴∠ABP+∠BAM=90°,
∴∠APB=90°,
∴点P在以AB为直径的圆上运动,设圆心为O,运动路径一条弧,是这个圆的,如图所示:
连接OC交圆O于P,此时PC最小,
∵AB=4,
∴OP=OB=2,
由勾股定理得:OC==2,
∴PC=OC﹣OP=2﹣2;
故答案为:2﹣2.
19.解:连接AP,
∵∠BAC=90°,PE⊥AB,PF⊥AC,
∴∠BAC=∠AEP=∠AFP=90°,
∴四边形AFPE是矩形,
∴EF=AP,
要使EF最小,只要AP最小即可,
当AP⊥BC时,AP最小,
在Rt△BAC中,∠BAC=90°,AB=6,BC=10,
由勾股定理得:AC===8,
由三角形面积公式得:△ABC的面积=×AB×AC=×BC×AP,
∴AP===4.8,
即EF=4.8,
故答案为:4.8.
20.解:①∵BM⊥AC于点M,CN⊥AB于点N,P为BC边的中点,
∴PM=BC,PN=BC,
∴PM=PN,故①正确;
②在△ABM与△ACN中,
∵∠A=∠A,∠AMB=∠ANC=90°,
∴△ABM∽△ACN,
∴=,
∴=,故②正确;
③∵∠A=60°,BM⊥AC于点M,CN⊥AB于点N,
∴∠ABM=∠ACN=30°,
在△ABC中,∠BCN+∠CBM=180°﹣60°﹣30°×2=60°,
∵点P是BC的中点,BM⊥AC,CN⊥AB,
∴PM=PN=PB=PC,
∴∠BPN=2∠BCN,∠CPM=2∠CBM,
∴∠BPN+∠CPM=2(∠BCN+∠CBM)=2×60°=120°,
∴∠MPN=60°,
∴△PMN是等边三角形,故③正确;
∵BN=CP,BP=CP(P为BC的中点),
∴BN=BP,
∵∠BPN=90°,
∴∠ABC=45°,
∵∠A=60°,
∴∠ACB=180°﹣∠A﹣∠ABC=75°,故④正确;
故答案为:①②③④.
三.解答题
21.解:原式=÷(﹣)
=?
=﹣,
∵a﹣2≠0,a﹣3≠0,a+3≠0,
∴a≠2,a≠±3,
∴当a=﹣2时,原式=﹣=﹣.
22.解:(1)如图2中,正方形PQMN即为所求作.
(2)能,拼成正方形,边长为,如图3所示.
23.解:(1)本次调查的人数为:20÷10%=200,
打卡5天的学生有:200﹣10﹣20﹣20﹣40﹣60=50(人),
故a=5,b=6,
补全的条形统计图如右图所示,
故答案为:5,6;
(2)1200×=900(人),
即初2020级学生中体育锻炼合格的有900人;
(3)由题意可得,
漏掉的这名学生坚持打卡天数最少是5天.
24.(1)证明:∵四边形ABCD是平行四边形,
∴AB=CD,AD=BC,
∵∠BAC=∠BCA,
∴AB=BC,
∴AB=CD=AD=BC,
∴四边形ABCD是菱形,
∴AC⊥BD,
∴∠DOC=90°,
∵CE∥BD,
∴∠OCE=90°,
同理可得∠ODE=90°,
∴四边形OEDC是矩形;
(2)解:过点E作EF垂直BC交BC延长线于点F,
∵∠BCA=60°,
∴∠BCD=120°,
∴∠ECF=120°﹣90°=30°,
∵BC=4,
∴BO=OD=6,
∴OD=CE=6,
∴EF=3,CF=3,
∴tan∠EBC==.
25.解:(1)学校离他家1000米,从出发到学校,王老师共用了25分钟;王老师吃早餐用了20﹣10=10分钟
故答案为:1000,25,10;
(2)根据图象可得:,所以吃完早餐以后速度快;
(3)(1000﹣500)÷(25﹣20)=100(米/分)
答:吃完早餐后的平均速度是100米/分.
26.解:(1)如图1,
在正方形ABCD和正方形DEFG中,∠ADC=∠EDG=90°,
∴∠ADE+∠EDG=∠ADC+∠ADE,
即∠ADG=∠CDE,
∵DG=DE,DA=DC,
∴△GDA≌△EDC(SAS),
∴AG=CE,∠GAD=∠ECD,
∵∠COD=∠AOH,
∴∠AHO=∠CDO=90°,
∴AG⊥CE,
故答案为:相等,垂直;
(2)不成立,CE=2AG,AG⊥CE,理由如下:
如图2,由(1)知,∠EDC=∠ADG,
∵AD=2DG,AB=2DE,AD=DE,
∴,==,
∴=,
∴△GDA∽△EDC,
∴=,即CE=2AG,
∵△GDA∽△EDC,
∴∠ECD=∠GAD,
∵∠COD=∠AOH,
∴∠AHO=∠CDO=90°,
∴AG⊥CE;
(3)①当点E在线段AG上时,如图3,
在Rt△EGD中,DG=3,ED=4,则EG=5,
过点D作DP⊥AG于点P,
∵∠DPG=∠EDG=90°,∠DGP=∠EGD,
∴△DGP∽△EGD,
∴=,即,
∴PD=,PG=,
则AP===,
则AE=AG﹣GE=AP+GP﹣GE=+﹣5=;
②当点G在线段AE上时,如图4,
过点D作DP⊥AG于点P,
∵∠DPG=∠EDG=90°,∠DGP=∠EGD,
同理得:PD=,AP=,
由勾股定理得:PE==,
则AE=AP+PE=+=;
综上,AE的长为.
27.解:(1)设直线AC的解析式是y=kx+b,
根据题意得:,
解得:.
则直线AC的解析式是:y=﹣x+6;
(2)∵C(0,6),A(4,2),
∴OC=6,
∴S△OAC=×6×4=12;
(3)设OA的解析式是y=mx,则4m=2,
解得:m=.
则直线的解析式是:y=x,
∵当△OMC的面积是△OAC的面积的时,
∴M到y轴的距离是×4=1,
∴点M的横坐标为1或﹣1;
当M的横坐标是:1,
在y=x中,当x=1时,y=,则M的坐标是(1,);
在y=﹣x+6中,x=1则y=5,则M的坐标是(1,5).
则M的坐标是:M1(1,)或M2(1,5).
当M的横坐标是:﹣1,
在y=﹣x+6中,当x=﹣1时,y=7,则M的坐标是(﹣1,7).
综上所述:M的坐标是:M1(1,)或M2(1,5)或M3(﹣1,7).
同课章节目录
