2.2 向心力 课件—粤教版高中物理必修二16张PPT
文档属性
| 名称 | 2.2 向心力 课件—粤教版高中物理必修二16张PPT |

|
|
| 格式 | zip | ||
| 文件大小 | 417.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 粤教版 | ||
| 科目 | 物理 | ||
| 更新时间 | 2021-05-28 00:00:00 | ||
图片预览






文档简介
(共17张PPT)
第二章第二节
向心力
(第二课时)
一、定义:
质点沿圆周运动,在相等的时间里通过的圆弧长
度相等。
二、描述运动的物理量:
线速度:
角速度:
周期:
频率:
向心加速度
大小:
方向:
始终指向圆心
向心力
始终指向圆心
大小:
方向:
周期性的非匀变速曲线运动。
三、匀速圆周运动性质是:
本章知识要点回顾
ω
O
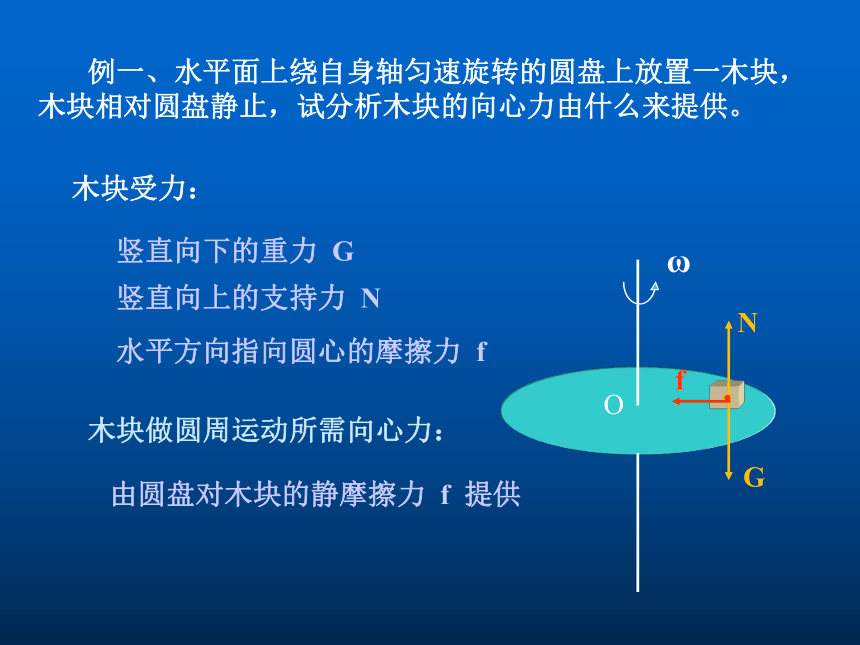
例一、水平面上绕自身轴匀速旋转的圆盘上放置一木块,木块相对圆盘静止,试分析木块的向心力由什么来提供。
木块受力:
竖直向下的重力
G
G
竖直向上的支持力
N
N
水平方向指向圆心的摩擦力
f
木块做圆周运动所需向心力:
f
由圆盘对木块的静摩擦力
f
提供
f
f
f
f
f
f
例二、试分析在竖直放置光滑圆锥内做匀速圆周运动小球所需的向心力。(杂技节目中的飞车走壁现象中的稳定状态)
小球受力:
竖直向下的重力
G
垂直圆锥面的支持力
N
G
N
F
小球的向心力:
由重力和支持力的合力提供
例三、讨论火车转弯时所需向心力。
1、内外轨道一样高时:
F
向心力
F
由外侧轨道对铁轨
的压力提供
2、当外轨略高于内轨时:
火车受力:
竖直向下的重力
G
G
垂直轨道面的支持力
N
N
F
火车的向心力:
由G和N的合力提供
当
时,车轮对内外轨都无压力。
在外轨略高于内轨时,火车转弯时的速度
v
G
N
F
火车的向心力:
由G和N的合力提供
(1)当
时,车轮
对内外轨都无压力。
火车行驶速率v>v规定
(2)当火车行驶速率v>v规定时,
(3)当火车行驶速率vG
N
N‘
火车行驶速率vG
N
N’
外轨对轮缘有侧压力;
内轨对轮缘有侧压力。
处理匀速圆周运动问题的一般步骤:
(1)明确对象,找出圆周平面,确定圆心及半径;
(2)进行受力分析,画出受力图;
(3)求出指向圆心方向的合力,即向心力;
(4)用牛顿第二定律
结合匀速圆周运的特点列方程求解。
例四、小球做圆锥摆时细绳长L,与竖直方向成θ角,求小球做匀速圆周运动的角速度ω。
O‘
O
mg
T
F
小球受力:
竖直向下的重力G
沿绳方向的拉力T
小球的向心力:
由T和G的合力提供
解:
θ
L
小球做圆周运动的半径
由牛顿第二定律:
即:
例五、质量为m的汽车以恒定的速率v通过半径均为r的拱桥和凹型地面,如图所示,求在A点和B点,汽车对路面的压力分别是多少?
A
B
解:
汽车通过A、B时,受力情况如图。
汽车通过A点时:
G
汽车通过B点时:
G
NB
NA
h
h
NA’
NB’
由牛顿第二定律:
由牛顿第三定律:
由牛顿第二定律:
由牛顿第三定律:
例六、如图要使小球滑到圆形轨道顶端不掉下来,小球在轨道顶端的最小速度应当是多大?已知轨道半径为R。
v
R
解:小球在最高点的受力情况如图
由等式可看出,由于m
、
R一定,所以
v
越小,N
就越小;当N=0时,小球可具有最小速度为
(此时,仅由重力提供其向心力)。
G
N
时,物体作离心运动;
时,物体靠近圆心运动。
v
R
时,物体作圆周运动;
小结:
一、处理匀速圆周运动问题的一般步骤:
(1)明确对象,找出圆周平面,确定圆心;
(2)进行受力分析,画出受力分析图;
(3)求出在半径方向的合力,即向心力;
二、用牛顿第二定律的瞬时对应关系,分析做圆周运动的条件:
时,物体作圆周运动;
时,物体作离心运动;
时,物体靠近圆心运动。
(4)用牛顿第二定律
结合匀速圆周运的特点列方程求解。
小结:
3、圆周运动主要有水平面运动和竖直面内运动典型情形。
竖直内的圆周运动实际上往往是变速率的运动,在切线方向还应当有力改变速率大小。(此时向心力不等于其合力)
竖直面内的圆周运动分成运动物体在圆周内、外两种情况,在运动的最高点有临界速度的计算问题值得我们留意。
作业:配套练习习题
(见本节附录习题)
第二章第二节
向心力
(第二课时)
一、定义:
质点沿圆周运动,在相等的时间里通过的圆弧长
度相等。
二、描述运动的物理量:
线速度:
角速度:
周期:
频率:
向心加速度
大小:
方向:
始终指向圆心
向心力
始终指向圆心
大小:
方向:
周期性的非匀变速曲线运动。
三、匀速圆周运动性质是:
本章知识要点回顾
ω
O
例一、水平面上绕自身轴匀速旋转的圆盘上放置一木块,木块相对圆盘静止,试分析木块的向心力由什么来提供。
木块受力:
竖直向下的重力
G
G
竖直向上的支持力
N
N
水平方向指向圆心的摩擦力
f
木块做圆周运动所需向心力:
f
由圆盘对木块的静摩擦力
f
提供
f
f
f
f
f
f
例二、试分析在竖直放置光滑圆锥内做匀速圆周运动小球所需的向心力。(杂技节目中的飞车走壁现象中的稳定状态)
小球受力:
竖直向下的重力
G
垂直圆锥面的支持力
N
G
N
F
小球的向心力:
由重力和支持力的合力提供
例三、讨论火车转弯时所需向心力。
1、内外轨道一样高时:
F
向心力
F
由外侧轨道对铁轨
的压力提供
2、当外轨略高于内轨时:
火车受力:
竖直向下的重力
G
G
垂直轨道面的支持力
N
N
F
火车的向心力:
由G和N的合力提供
当
时,车轮对内外轨都无压力。
在外轨略高于内轨时,火车转弯时的速度
v
G
N
F
火车的向心力:
由G和N的合力提供
(1)当
时,车轮
对内外轨都无压力。
火车行驶速率v>v规定
(2)当火车行驶速率v>v规定时,
(3)当火车行驶速率v
N
N‘
火车行驶速率v
N
N’
外轨对轮缘有侧压力;
内轨对轮缘有侧压力。
处理匀速圆周运动问题的一般步骤:
(1)明确对象,找出圆周平面,确定圆心及半径;
(2)进行受力分析,画出受力图;
(3)求出指向圆心方向的合力,即向心力;
(4)用牛顿第二定律
结合匀速圆周运的特点列方程求解。
例四、小球做圆锥摆时细绳长L,与竖直方向成θ角,求小球做匀速圆周运动的角速度ω。
O‘
O
mg
T
F
小球受力:
竖直向下的重力G
沿绳方向的拉力T
小球的向心力:
由T和G的合力提供
解:
θ
L
小球做圆周运动的半径
由牛顿第二定律:
即:
例五、质量为m的汽车以恒定的速率v通过半径均为r的拱桥和凹型地面,如图所示,求在A点和B点,汽车对路面的压力分别是多少?
A
B
解:
汽车通过A、B时,受力情况如图。
汽车通过A点时:
G
汽车通过B点时:
G
NB
NA
h
h
NA’
NB’
由牛顿第二定律:
由牛顿第三定律:
由牛顿第二定律:
由牛顿第三定律:
例六、如图要使小球滑到圆形轨道顶端不掉下来,小球在轨道顶端的最小速度应当是多大?已知轨道半径为R。
v
R
解:小球在最高点的受力情况如图
由等式可看出,由于m
、
R一定,所以
v
越小,N
就越小;当N=0时,小球可具有最小速度为
(此时,仅由重力提供其向心力)。
G
N
时,物体作离心运动;
时,物体靠近圆心运动。
v
R
时,物体作圆周运动;
小结:
一、处理匀速圆周运动问题的一般步骤:
(1)明确对象,找出圆周平面,确定圆心;
(2)进行受力分析,画出受力分析图;
(3)求出在半径方向的合力,即向心力;
二、用牛顿第二定律的瞬时对应关系,分析做圆周运动的条件:
时,物体作圆周运动;
时,物体作离心运动;
时,物体靠近圆心运动。
(4)用牛顿第二定律
结合匀速圆周运的特点列方程求解。
小结:
3、圆周运动主要有水平面运动和竖直面内运动典型情形。
竖直内的圆周运动实际上往往是变速率的运动,在切线方向还应当有力改变速率大小。(此时向心力不等于其合力)
竖直面内的圆周运动分成运动物体在圆周内、外两种情况,在运动的最高点有临界速度的计算问题值得我们留意。
作业:配套练习习题
(见本节附录习题)
同课章节目录
- 第一章 抛体运动
- 第01节 什么是抛体运动
- 第02节 运动的合成与分解
- 第03节 竖直方向的抛体运动
- 第04节 平抛运动
- 第05节 斜抛运动
- 第二章 圆周运动
- 第01节 匀速圆周运动
- 第02节 向心力
- 第03节 离心现象及其应用
- 第三章 万有引力定律及其应用
- 第01节 万有引力定律
- 第02节 万有引力定律的应用
- 第03节 飞向太空
- 第四章 机械能和能源
- 第01节 功
- 第02节 动能 势能
- 第03节 探究外力做功与物体动能变化的关系
- 第04节 机械能守恒定律
- 第05节 验证机械能守恒定律
- 第06节 能量 能量转化与守恒定律
- 第07节 功率
- 第08节 能源的开发与利用
- 第五章 经典力学与物理学的革命
- 第01节 经典力学的成就与局限性
- 第02节 经典时空观与相对论时空观
- 第03节 量子化现象
- 第04节 物理学——人类文明进步的阶梯
