北师大版数学四年级上册 4.2 加法交换律和乘法交换律 课件(21页PPT)
文档属性
| 名称 | 北师大版数学四年级上册 4.2 加法交换律和乘法交换律 课件(21页PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 280.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-28 00:00:00 | ||
图片预览







文档简介
第2课时 加法交换律和乘法交换律
四 运算律
一、情境引入
小宁在写字
“小宁”和“字”可以交换吗?
不能,交换后就变成“字在写小宁”。
数字36中的“3”和“6”可以交换吗?
不能,交换后就变成63。36和63是两个不同的数字。
二、学习新课
仔细观察,这两个算式有什么相同点和不同点?
相同点:两个加数都分别是4和6,和都是10;
不同点:两个加数的位置不同。
二、学习新课
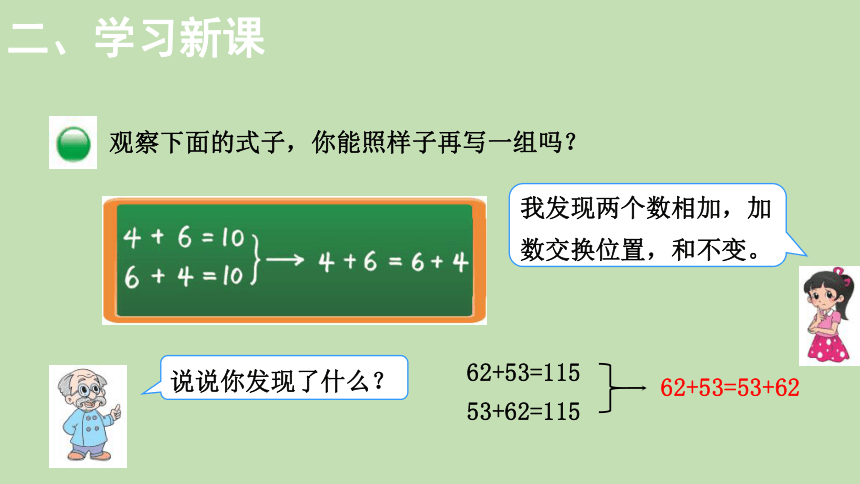
观察下面的式子,你能照样子再写一组吗?
62+53=115
53+62=115
62+53=53+62
说说你发现了什么?
二、学习新课
观察下面的式子,你能照样子再写一组吗?
62+53=115
53+62=115
62+53=53+62
说说你发现了什么?
我发现两个数相加,加数交换位置,和不变。
二、学习新课
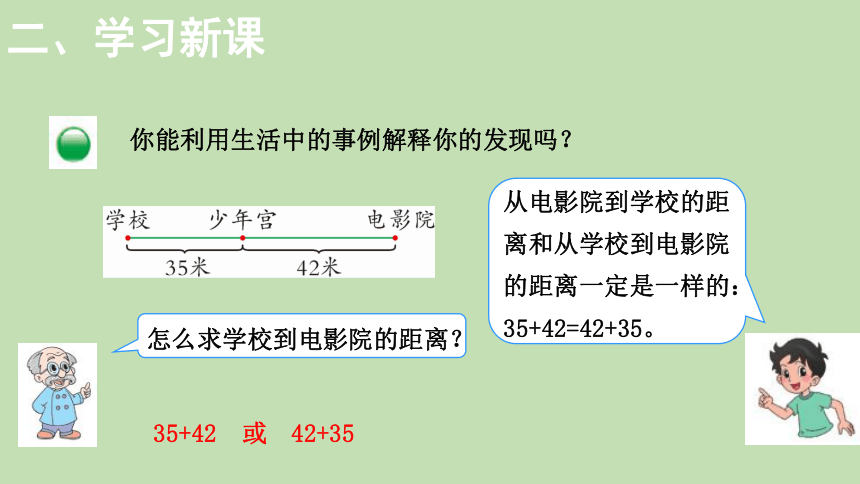
你能利用生活中的事例解释你的发现吗?
从电影院到学校的距离和从学校到电影院的距离一定是一样的:35+42=42+35。
怎么求学校到电影院的距离?
35+42
42+35
或
二、学习新课
用a、b代表两个数,你能写出上面发现的规律吗?
a+b=b+a
加法交换律
62+53=53+62
4+6=6+4
( )+270=270+80
400+500=( )+( )
400
500
80
二、学习新课
加法交换律
你能结合今天学习的知识解释下面计算的道理吗?
3 5 8
+ 2 7 6
1
1
2 7 6
+ 3 5 8
1
1
358+276=634
验算:
应用加法交换律,可以验算加法计算是否准确。
a+b=b+a
6
3
4
6
3
4
加法交换律:两个数相加,交换加数的位置,它们的和不变。用字母表示为:a+b=b+a。
二、学习新课
通过前面的学习,你能对加法交换律进行总结吗?
二、学习新课
仔细观察,这两个算式有什么相同点和不同点?
相同点:两个乘数都分别是3和5,积都是15;
不同点:两个乘数的位置不同。
二、学习新课
观察下面的式子,你能照样子再写一组吗?
说说你发现了什么?
7×9=63
9×7=63
7×9=9×7
二、学习新课
观察下面的式子,你能照样子再写一组吗?
说说你发现了什么?
7×9=63
9×7=63
7×9=9×7
我发现两个数相乘,乘数交换位置,积不变。
二、学习新课
你能利用生活中的事例解释你的发现吗?
横着看,每排6把,有5排;竖着看,每列5把,有6列。实际上是一样的:6×5=5×6。
怎么求一共有多少把椅子?
6×5
5×6
或
二、学习新课
用a、b代表两个数,你能写出上面发现的规律吗?
a×b=b×a
乘法交换律
7×9=9×7
3×5=5×3
( )×713=( )×84
119×74=( )×( )
119
74
84
713
二、学习新课
乘法交换律
你能结合今天学习的知识解释下面计算的道理吗?
1 0 7
× 5
5 3 5
5×107=535
应用乘法交换律,可以验算乘法计算是否准确。
a×b=b×a
乘法交换律:两个数相乘,交换乘数的位置,它们的积不变。用字母表示为:a×b=b×a。
二、学习新课
通过前面的学习,你能对乘法交换律进行总结吗?
三、巩固反馈
45+76 = +45
28+13= +
+ = +
45×102=102×
296×200= ×
× = ×
2.运用加法交换律和乘法交换律填一填。
76
13
28
45
200
296
答案不唯一
答案不唯一
52
23
23
52
36
47
47
36
三、巩固反馈
918+395
35×27
3.计算下列各题,并运用加法交换律或乘法交换律进行验算。
三、巩固反馈
3.计算下列各题,并运用加法交换律或乘法交换律进行验算。
918+395
验算:
9 1 8
3 9 5
+
1
1
3
1
3
1
3 9 5
9 1 8
+
1
1
3
1
3
1
=1313
1
1
三、巩固反馈
3.计算下列各题,并运用加法交换律或乘法交换律进行验算。
35×27
验算:
3 5
2 7
×
2
4
5
=945
7
0
9
4
5
2 7
3 5
×
1
3
5
8
1
9
4
5
四、课堂小结
乘法交换律:两个数相乘,交换乘数的位置,它们的积不变。用字母表示为:a×b=b×a。
加法交换律:两个数相加,交换加数的位置,它们的和不变。用字母表示为:a+b=b+a。
四 运算律
一、情境引入
小宁在写字
“小宁”和“字”可以交换吗?
不能,交换后就变成“字在写小宁”。
数字36中的“3”和“6”可以交换吗?
不能,交换后就变成63。36和63是两个不同的数字。
二、学习新课
仔细观察,这两个算式有什么相同点和不同点?
相同点:两个加数都分别是4和6,和都是10;
不同点:两个加数的位置不同。
二、学习新课
观察下面的式子,你能照样子再写一组吗?
62+53=115
53+62=115
62+53=53+62
说说你发现了什么?
二、学习新课
观察下面的式子,你能照样子再写一组吗?
62+53=115
53+62=115
62+53=53+62
说说你发现了什么?
我发现两个数相加,加数交换位置,和不变。
二、学习新课
你能利用生活中的事例解释你的发现吗?
从电影院到学校的距离和从学校到电影院的距离一定是一样的:35+42=42+35。
怎么求学校到电影院的距离?
35+42
42+35
或
二、学习新课
用a、b代表两个数,你能写出上面发现的规律吗?
a+b=b+a
加法交换律
62+53=53+62
4+6=6+4
( )+270=270+80
400+500=( )+( )
400
500
80
二、学习新课
加法交换律
你能结合今天学习的知识解释下面计算的道理吗?
3 5 8
+ 2 7 6
1
1
2 7 6
+ 3 5 8
1
1
358+276=634
验算:
应用加法交换律,可以验算加法计算是否准确。
a+b=b+a
6
3
4
6
3
4
加法交换律:两个数相加,交换加数的位置,它们的和不变。用字母表示为:a+b=b+a。
二、学习新课
通过前面的学习,你能对加法交换律进行总结吗?
二、学习新课
仔细观察,这两个算式有什么相同点和不同点?
相同点:两个乘数都分别是3和5,积都是15;
不同点:两个乘数的位置不同。
二、学习新课
观察下面的式子,你能照样子再写一组吗?
说说你发现了什么?
7×9=63
9×7=63
7×9=9×7
二、学习新课
观察下面的式子,你能照样子再写一组吗?
说说你发现了什么?
7×9=63
9×7=63
7×9=9×7
我发现两个数相乘,乘数交换位置,积不变。
二、学习新课
你能利用生活中的事例解释你的发现吗?
横着看,每排6把,有5排;竖着看,每列5把,有6列。实际上是一样的:6×5=5×6。
怎么求一共有多少把椅子?
6×5
5×6
或
二、学习新课
用a、b代表两个数,你能写出上面发现的规律吗?
a×b=b×a
乘法交换律
7×9=9×7
3×5=5×3
( )×713=( )×84
119×74=( )×( )
119
74
84
713
二、学习新课
乘法交换律
你能结合今天学习的知识解释下面计算的道理吗?
1 0 7
× 5
5 3 5
5×107=535
应用乘法交换律,可以验算乘法计算是否准确。
a×b=b×a
乘法交换律:两个数相乘,交换乘数的位置,它们的积不变。用字母表示为:a×b=b×a。
二、学习新课
通过前面的学习,你能对乘法交换律进行总结吗?
三、巩固反馈
45+76 = +45
28+13= +
+ = +
45×102=102×
296×200= ×
× = ×
2.运用加法交换律和乘法交换律填一填。
76
13
28
45
200
296
答案不唯一
答案不唯一
52
23
23
52
36
47
47
36
三、巩固反馈
918+395
35×27
3.计算下列各题,并运用加法交换律或乘法交换律进行验算。
三、巩固反馈
3.计算下列各题,并运用加法交换律或乘法交换律进行验算。
918+395
验算:
9 1 8
3 9 5
+
1
1
3
1
3
1
3 9 5
9 1 8
+
1
1
3
1
3
1
=1313
1
1
三、巩固反馈
3.计算下列各题,并运用加法交换律或乘法交换律进行验算。
35×27
验算:
3 5
2 7
×
2
4
5
=945
7
0
9
4
5
2 7
3 5
×
1
3
5
8
1
9
4
5
四、课堂小结
乘法交换律:两个数相乘,交换乘数的位置,它们的积不变。用字母表示为:a×b=b×a。
加法交换律:两个数相加,交换加数的位置,它们的和不变。用字母表示为:a+b=b+a。
同课章节目录
- 一 认识更大的数
- 1 数一数
- 2 认识更大的数
- 3 人口普查
- 4 国土面积
- 5 近似数
- 6 从结绳计数说起
- 二 线与角
- 1 线的认识
- 2 相交与垂直
- 3 平移与平行
- 4 旋转与角
- 5 角的度量(一)
- 6 角的度量(二)
- 三 乘法
- 1 卫星运行时间
- 2 有多少名观众
- 3 神奇的计算工具
- 4 有趣的算式
- 四 运算律
- 1 买文具
- 2 加法交换律和乘法交换律
- 3 加法结合律
- 4 乘法结合律
- 5 乘法分配律
- 五 方向与位置
- 1 去图书馆
- 2 确定位置
- 六 除法
- 1 买文具
- 2 参观花圃
- 3 秋游
- 4 商不变的规律
- 5 路程、时间与速度
- 七 生活中的负数
- 1 温度
- 2 正负数
- 数学好玩
- 1 滴水试验
- 2 编码
- 3 数图形的学问
- 八 可能性
- 1 不确定性
- 2 摸球游戏
