北师大版数学四年级上册 4.5 乘法分配律 课件(26页PPT)
文档属性
| 名称 | 北师大版数学四年级上册 4.5 乘法分配律 课件(26页PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 539.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-28 08:36:41 | ||
图片预览




文档简介
第5课时 乘法分配律
四 运算律
一、情境引入
两个数相加,交换加数的位置,和不变,叫作加法交换律。
什么是加法交换律?
两个数相乘,交换乘数的位置,积不变,叫作乘法交换律。
什么是乘法交换律?
一、情境引入
什么是加法结合律?
在加法中,三个数相加,先把前两个数相加,再与第三个数相加;或者先把后两个数相加,再与第一个数相加,它们的和不变。
什么是乘法结合律?
在乘法中,三个数相乘,先把前两个数相乘,再与第三个数相乘;或者先把后两个数相乘,再与第一个数相乘,它们的积不变。
二、学习新课
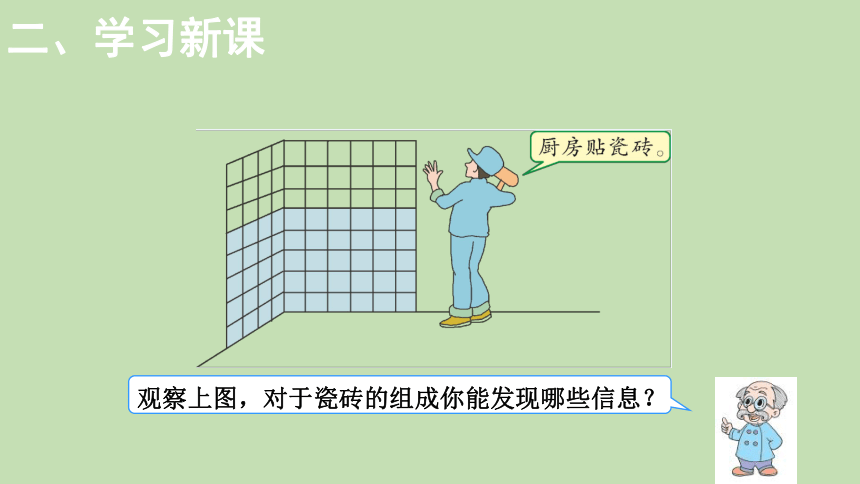
观察上图,对于瓷砖的组成你能发现哪些信息?
二、学习新课
贴了多少块瓷砖?说说你是怎样算的。
二、学习新课
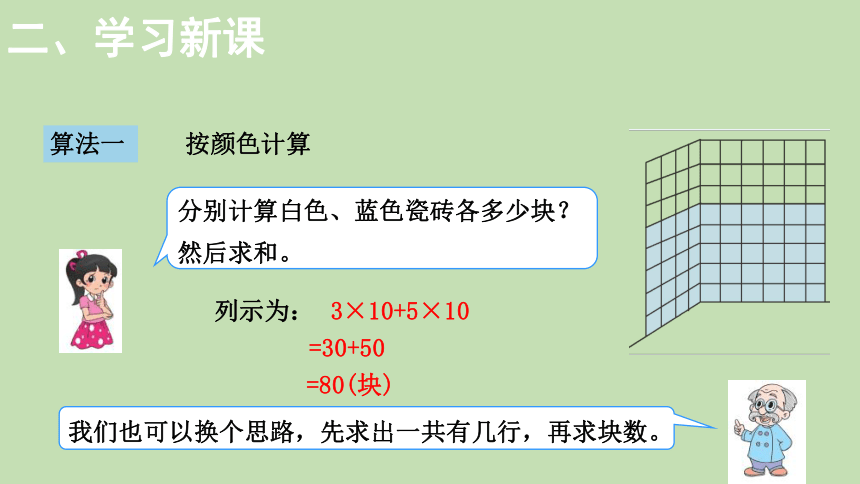
算法一
按颜色计算
分别计算白色、蓝色瓷砖各多少块?然后求和。
3×10+5×10
我们也可以换个思路,先求出一共有几行,再求块数。
列示为:
=30+50
=80(块)
二、学习新课
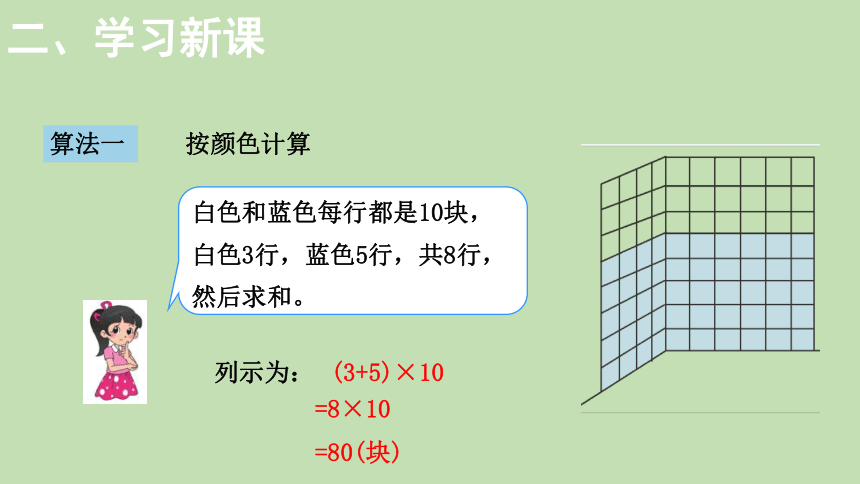
算法一
按颜色计算
白色和蓝色每行都是10块,白色3行,蓝色5行,共8行,然后求和。
(3+5)×10
列示为:
=8×10
=80(块)
二、学习新课
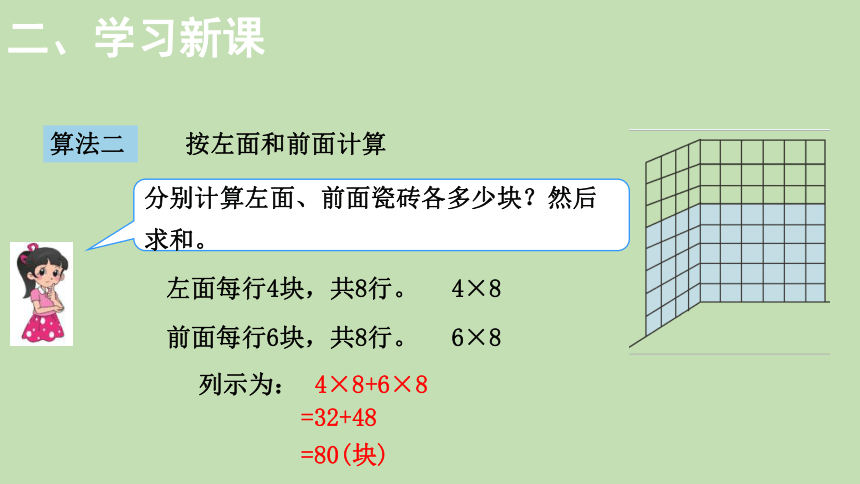
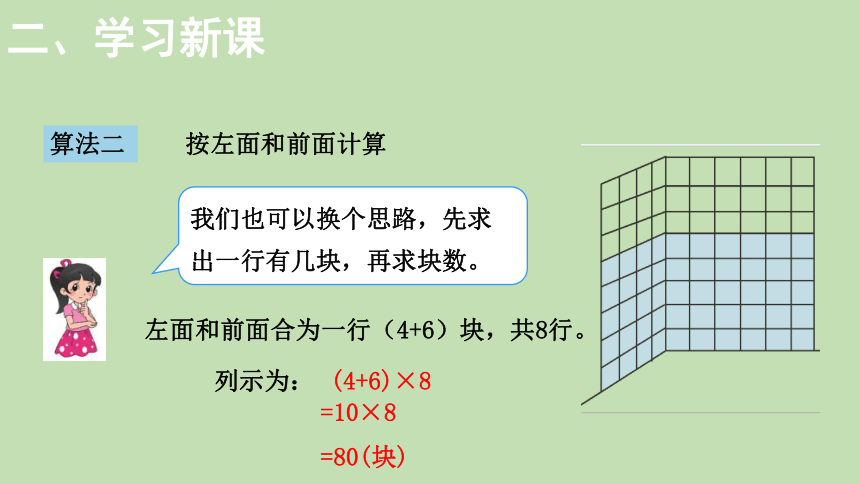
算法二
按左面和前面计算
4×8+6×8
分别计算左面、前面瓷砖各多少块?然后求和。
列示为:
左面每行4块,共8行。
4×8
前面每行6块,共8行。
6×8
=32+48
=80(块)
二、学习新课
算法二
按左面和前面计算
我们也可以换个思路,先求出一行有几块,再求块数。
(4+6)×8
列示为:
左面和前面合为一行(4+6)块,共8行。
=10×8
=80(块)
二、学习新课
观察上面两组算式,你有什么发现?
3×10+5×10
=30+50
=80(块)
(3+5)×10
=8×10
=80(块)
4×8+6×8
=32+48
=80(块)
(4+6)×8
=10×8
=80(块)
我发现5×10+3×10=(5+3)×10。
我发现8×4+8×6=8×(4+6)。
二、学习新课
观察刚列举的这些式子,它们有什么特点?
(40+4)×25和40×25+4×25
42×64+42×36和42×(64+36)
观察上面的式子,你还可以再举一些类似的例子吗?
等号左边算式中的两个加数,就是等号右边算式中两个不同的乘数;等号左边算式中的一个乘数,就是等号右边算式中两个相同的乘数。
二、学习新课
用a、b、c代表三个数,你能写出上面发现的规律吗?想一想,认一认。
(a+b)×c=a×c+b×c
乘法分配律
(4+6)×8=4×8+6×8
(3+5)×10=3×10+5×10
二、学习新课
请你结合4×9+6×9这个算式说明乘法分配律是成立的。
我用画图的方法。
二、学习新课
观察(80+4)×25的特点并计算。
(80+4)×25
=80×25+4×25
=2000+100
=2100
可以用80×25,再用4×25,然后两积相加。
我用乘法分配律 。
二、学习新课
观察34×72+34×28的特点并计算。
表示72个34加上28个34,一共有100个34。
我用乘法分配律 。
两个乘法算式中都有34。
二、学习新课
观察34×72+34×28的特点并计算。
34×72+34×28
=34×(72+28)
=34×100
=3400
你发现了什么?
二、学习新课
如果已知(a+b)×c这种形式,且a乘c和b乘c比较简便,就用a×c+b×c来计算;
如果已知a×c+b×c这种形式,且a加b的和是一个整十、整百的数,用(a+b)×c这种形式计算比较简便。
乘法分配律:两个数的和与一个数相乘,可以把这两个数分别与这个数相乘,再把积相加,结果不变。
三、巩固反馈
3.观察下面算式的特点并计算。
(20+4)×25
35×37+65×37
19×66+81×66
125×(80+8)
32×(200+3)
12×26+12×4
12×65+65×88
8×(125+9)
39×6+39×54
(20+4)×25
=600
35×37+65×37
=(35+65)×37
19×66+81×66
=(19+81)×66
=20×25+4×25
=500+100
3.观察下面算式的特点并计算。
=100×37
=3700
=100×66
=6600
三、巩固反馈
三、巩固反馈
3.观察下面算式的特点并计算。
32×(200+3)
=32×200+32×3
12×26+12×4
=12×(26+4)
125×(80+8)
=125×80+125×8
=6400+96
=6496
=12×30
=360
=10000+1000
=11000
三、巩固反馈
3.观察下面算式的特点并计算。
12×65+65×88
=(12+88)×65
8×(125+9)
=8×125+8×9
39×6+39×54
=39×(6+54)
=100×65
=6500
=1000+72
=1072
=39×60
=2340
三、巩固反馈
4.水果丰收了。
(1) 共有多少箱水果?
(2) 这些水果一共能卖多少元?
三、巩固反馈
4.水果丰收了。
(1) 共有多少箱水果?
解法一:
解法二:
(24+26)×25=50×25=1250(箱)
24×25+26×25=600+650=1250(箱)
答:共有1250箱水果。
三、巩固反馈
4.水果丰收了。
(2) 这些水果一共能卖多少元?
解法一:
解法二:
(24×80+26×70)×25=93500(元)
24×25×80+26×25×70=93500(元)
答:这些水果一共能卖93500元。
三、巩固反馈
5.妈妈给淘气订了一套可以自由组合的小柜子,每个小柜子18元,柜门上每张贴画2元,算一算,这套小柜子一共花了多少元?
解法一:
(18+2)×6=120(元)
解法二:
18×6+2×6=120(元)
答:这套小柜子一共花了120元。
四、课堂小结
乘法分配律:两个数的和与一个数相乘,可以把这两个数分别与这个数相乘,再把积相加,结果不变。用字母表示是:(a+b)×c=a×c+b×c。
四 运算律
一、情境引入
两个数相加,交换加数的位置,和不变,叫作加法交换律。
什么是加法交换律?
两个数相乘,交换乘数的位置,积不变,叫作乘法交换律。
什么是乘法交换律?
一、情境引入
什么是加法结合律?
在加法中,三个数相加,先把前两个数相加,再与第三个数相加;或者先把后两个数相加,再与第一个数相加,它们的和不变。
什么是乘法结合律?
在乘法中,三个数相乘,先把前两个数相乘,再与第三个数相乘;或者先把后两个数相乘,再与第一个数相乘,它们的积不变。
二、学习新课
观察上图,对于瓷砖的组成你能发现哪些信息?
二、学习新课
贴了多少块瓷砖?说说你是怎样算的。
二、学习新课
算法一
按颜色计算
分别计算白色、蓝色瓷砖各多少块?然后求和。
3×10+5×10
我们也可以换个思路,先求出一共有几行,再求块数。
列示为:
=30+50
=80(块)
二、学习新课
算法一
按颜色计算
白色和蓝色每行都是10块,白色3行,蓝色5行,共8行,然后求和。
(3+5)×10
列示为:
=8×10
=80(块)
二、学习新课
算法二
按左面和前面计算
4×8+6×8
分别计算左面、前面瓷砖各多少块?然后求和。
列示为:
左面每行4块,共8行。
4×8
前面每行6块,共8行。
6×8
=32+48
=80(块)
二、学习新课
算法二
按左面和前面计算
我们也可以换个思路,先求出一行有几块,再求块数。
(4+6)×8
列示为:
左面和前面合为一行(4+6)块,共8行。
=10×8
=80(块)
二、学习新课
观察上面两组算式,你有什么发现?
3×10+5×10
=30+50
=80(块)
(3+5)×10
=8×10
=80(块)
4×8+6×8
=32+48
=80(块)
(4+6)×8
=10×8
=80(块)
我发现5×10+3×10=(5+3)×10。
我发现8×4+8×6=8×(4+6)。
二、学习新课
观察刚列举的这些式子,它们有什么特点?
(40+4)×25和40×25+4×25
42×64+42×36和42×(64+36)
观察上面的式子,你还可以再举一些类似的例子吗?
等号左边算式中的两个加数,就是等号右边算式中两个不同的乘数;等号左边算式中的一个乘数,就是等号右边算式中两个相同的乘数。
二、学习新课
用a、b、c代表三个数,你能写出上面发现的规律吗?想一想,认一认。
(a+b)×c=a×c+b×c
乘法分配律
(4+6)×8=4×8+6×8
(3+5)×10=3×10+5×10
二、学习新课
请你结合4×9+6×9这个算式说明乘法分配律是成立的。
我用画图的方法。
二、学习新课
观察(80+4)×25的特点并计算。
(80+4)×25
=80×25+4×25
=2000+100
=2100
可以用80×25,再用4×25,然后两积相加。
我用乘法分配律 。
二、学习新课
观察34×72+34×28的特点并计算。
表示72个34加上28个34,一共有100个34。
我用乘法分配律 。
两个乘法算式中都有34。
二、学习新课
观察34×72+34×28的特点并计算。
34×72+34×28
=34×(72+28)
=34×100
=3400
你发现了什么?
二、学习新课
如果已知(a+b)×c这种形式,且a乘c和b乘c比较简便,就用a×c+b×c来计算;
如果已知a×c+b×c这种形式,且a加b的和是一个整十、整百的数,用(a+b)×c这种形式计算比较简便。
乘法分配律:两个数的和与一个数相乘,可以把这两个数分别与这个数相乘,再把积相加,结果不变。
三、巩固反馈
3.观察下面算式的特点并计算。
(20+4)×25
35×37+65×37
19×66+81×66
125×(80+8)
32×(200+3)
12×26+12×4
12×65+65×88
8×(125+9)
39×6+39×54
(20+4)×25
=600
35×37+65×37
=(35+65)×37
19×66+81×66
=(19+81)×66
=20×25+4×25
=500+100
3.观察下面算式的特点并计算。
=100×37
=3700
=100×66
=6600
三、巩固反馈
三、巩固反馈
3.观察下面算式的特点并计算。
32×(200+3)
=32×200+32×3
12×26+12×4
=12×(26+4)
125×(80+8)
=125×80+125×8
=6400+96
=6496
=12×30
=360
=10000+1000
=11000
三、巩固反馈
3.观察下面算式的特点并计算。
12×65+65×88
=(12+88)×65
8×(125+9)
=8×125+8×9
39×6+39×54
=39×(6+54)
=100×65
=6500
=1000+72
=1072
=39×60
=2340
三、巩固反馈
4.水果丰收了。
(1) 共有多少箱水果?
(2) 这些水果一共能卖多少元?
三、巩固反馈
4.水果丰收了。
(1) 共有多少箱水果?
解法一:
解法二:
(24+26)×25=50×25=1250(箱)
24×25+26×25=600+650=1250(箱)
答:共有1250箱水果。
三、巩固反馈
4.水果丰收了。
(2) 这些水果一共能卖多少元?
解法一:
解法二:
(24×80+26×70)×25=93500(元)
24×25×80+26×25×70=93500(元)
答:这些水果一共能卖93500元。
三、巩固反馈
5.妈妈给淘气订了一套可以自由组合的小柜子,每个小柜子18元,柜门上每张贴画2元,算一算,这套小柜子一共花了多少元?
解法一:
(18+2)×6=120(元)
解法二:
18×6+2×6=120(元)
答:这套小柜子一共花了120元。
四、课堂小结
乘法分配律:两个数的和与一个数相乘,可以把这两个数分别与这个数相乘,再把积相加,结果不变。用字母表示是:(a+b)×c=a×c+b×c。
同课章节目录
- 一 认识更大的数
- 1 数一数
- 2 认识更大的数
- 3 人口普查
- 4 国土面积
- 5 近似数
- 6 从结绳计数说起
- 二 线与角
- 1 线的认识
- 2 相交与垂直
- 3 平移与平行
- 4 旋转与角
- 5 角的度量(一)
- 6 角的度量(二)
- 三 乘法
- 1 卫星运行时间
- 2 有多少名观众
- 3 神奇的计算工具
- 4 有趣的算式
- 四 运算律
- 1 买文具
- 2 加法交换律和乘法交换律
- 3 加法结合律
- 4 乘法结合律
- 5 乘法分配律
- 五 方向与位置
- 1 去图书馆
- 2 确定位置
- 六 除法
- 1 买文具
- 2 参观花圃
- 3 秋游
- 4 商不变的规律
- 5 路程、时间与速度
- 七 生活中的负数
- 1 温度
- 2 正负数
- 数学好玩
- 1 滴水试验
- 2 编码
- 3 数图形的学问
- 八 可能性
- 1 不确定性
- 2 摸球游戏
