北师大版数学四年级上册 4.6运算律 练习四 课件(25页PPT)
文档属性
| 名称 | 北师大版数学四年级上册 4.6运算律 练习四 课件(25页PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 990.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-28 08:37:57 | ||
图片预览






文档简介
第6课时 练习四
四 运算律
一、基础练习
同学们经过本单元的学习,你掌握了简便方法计算了吗?试着算一算吧。
101×21=
25×16=
37×25×4=
2121
3700
400
二、指导练习
练习四
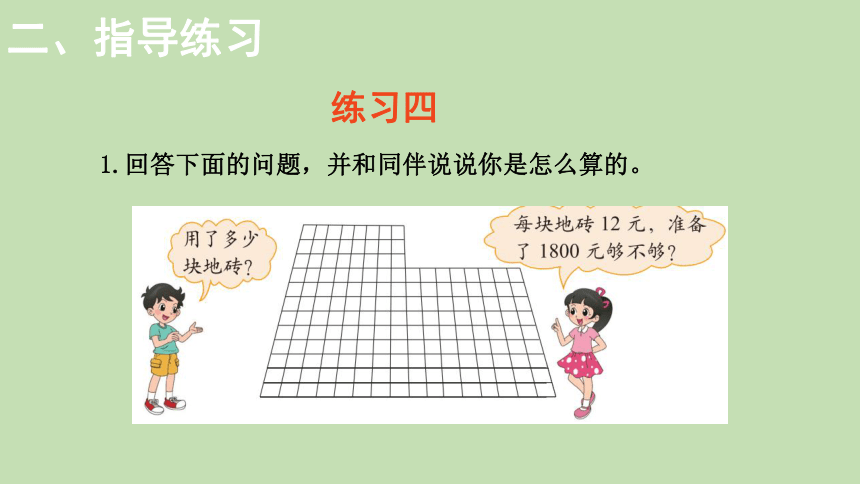
1.回答下面的问题,并和同伴说说你是怎么算的。
二、指导练习
观察图中地砖,我们可以怎样分割来进行计算地砖的块数?
算法一
按左面、右面计算
8×12+8×9
=8×(12+9)
=8×21
=168
左面每行8块,共12行。
8×12
前面每行8块,共9行。
8×9
二、指导练习
算法二
按前面、后面计算
16×9+8×3
分别计算前面、后面瓷砖各多少块?然后求和。
列示为:
左面每行16块,共9行。
16×9
前面每行8块,共3行。
8×3
=144+24
=168(块)
二、指导练习
算法三
按添补法计算
16×12-8×3
我们也可以换个思路,先将地砖空白部分补齐,再减去补的地砖数,来求地砖总块数。
列示为:
=192-24
=168(块)
补全后每行16块,共12行。
二、指导练习
168×12
2016>1800
所以准备了1800元不够。
=168×(10+2)
=168×10+168×2
=1680+336
=2016(元)
计算时,将12分成(10+2),利用乘法分配律,计算更简便。
计算地砖所需钱数:
二、指导练习
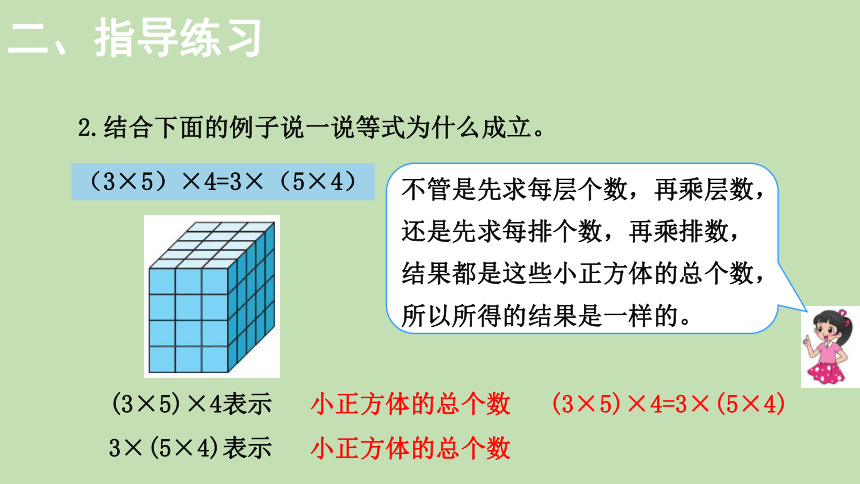
2.结合下面的例子说一说等式为什么成立。
(3×5)×4=3×(5×4)
3×(5×4)表示
(3×5)×4表示
小正方体的总个数
小正方体的总个数
(3×5)×4=3×(5×4)
不管是先求每层个数,再乘层数,还是先求每排个数,再乘排数,结果都是这些小正方体的总个数,所以所得的结果是一样的。
二、指导练习
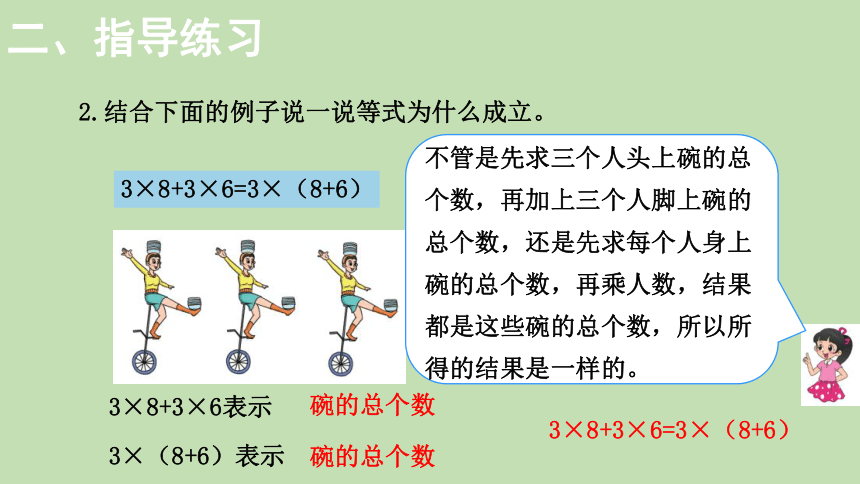
2.结合下面的例子说一说等式为什么成立。
3×8+3×6=3×(8+6)
3×(8+6)表示
3×8+3×6表示
碗的总个数
碗的总个数
3×8+3×6=3×(8+6)
不管是先求三个人头上碗的总个数,再加上三个人脚上碗的总个数,还是先求每个人身上碗的总个数,再乘人数,结果都是这些碗的总个数,所以所得的结果是一样的。
二、指导练习
4.
(1)这个花圃的篱笆长多少米?
(30+25)×2=110(米)
求篱笆的长相当于求这个花圃的什么?
周长
答:这个花圃的篱笆长110米。
二、指导练习
4.
(2)如果每平方米大约种40棵郁金香,这个花圃大约种了多少棵郁金香?
30×25=750(m2)
750×40=30000(棵)
答:这个花圃大约种了30000棵郁金香。
关于长方形面积的计算,花圃有多少平方米就有多少个40棵郁金香,从而求出这个花圃大约种了多少棵郁金香。
二、指导练习
5.连一连。
75×2×5
58+147+42
38×29+38
(100+4)×25
38×(29+1)
100×25+4×25
58+42+147
75×(2×5)
三、巩固练习
3.
85×82+82×15
5×289×2
(125×25)×4
25×97+25×3
378+527+73
(125+17)×8
58+39+42+61
76×25+25×24
167+289+33
三、巩固练习
3.
85×82+82×15
=(85+15)×82
5×289×2
=(5×2)×289
(125×25)×4
=125×(25×4)
=8200
=100×82
=10×289
=2890
=125×100
=12500
三、巩固练习
25×97+25×3
=25×(97+3)
378+527+73
=378+(527+73)
(125+17)×8
=125×8+17×8
=1000+136
=1136
=25×100
=2500
=378+600
=978
三、巩固练习
58+39+42+61
=(58+42)+(39+61)
76×25+25×24
=(76+24)×25
167+289+33
=289+(167+33)
=289+200
=489
=100+100
=200
=100×25
=2500
三、巩固练习
6.
(1)列出上述问题的算式,观察每一个算式乘数的变化,你能发现积的变化规律吗?
三、巩固练习
(1)12×2=24(千米)
通过观察得出的结论是:在乘法算式中,一个乘数不变,另一个乘数扩大几倍,积也就相应地扩大几倍。
12×4=48(千米)
12×6=72(千米)
三、巩固练习
(2)利用你发现的规律,能直接写出下列算式的得数吗?
150×20=3000
150×40=
150×60=
360×24=8640
360×12=
360×6=
4320
6000
9000
2160
三、巩固练习
7.(1)5×10-5×3=5×(10-3)成立吗?想办法验证你的想法。
三、巩固练习
由图意可知,一大张蝴蝶图片中共有10竖排,每竖排都有5个蝴蝶图案,可以用10竖排的总数(5×10)减去剪掉的3竖排的数量(5×3),列式为5×10-5×3;还可以先求剩几竖排(10-3),再求剩下的这些竖排有多少个蝴蝶图案,列式为5×(10-3)。因为两个式子求的都是剩下的蝴蝶图案的个数,所以5×10-5×3=5×(10-3)成立。
7.(1)5×10-5×3=5×(10-3)成立吗?想办法验证你的想法。
三、巩固练习
13×99
=13×(100-1)
=13×100-13×1
=1287
(2)你能看懂下面算式的道理吗?
在13×99中,因为99接近100,所以将13×99写成13×(100-1)的形式,运用乘法分配律计算。把算式写成13×100-13×1,即用100个13减去1个13,这样计算更加简便。
三、巩固练习
(3)你能使下面的计算变得简便吗?
206×14-6×14
=(206-6)×14
=200×14
=2800
72×99
=72×(100-1)
=72×100-72×1
=7128
四、课堂小结
两个数相加,交换加数的位置,和不变,叫作加法交换律。
两个数相乘,交换乘数的位置,积不变,叫作乘法交换律。
四、课堂小结
在加法中,三个数相加,先把前两个数相加,再与第三个数相加;或者先把后两个数相加,再与第一个数相加,它们的和不变。
在乘法中,三个数相乘,先把前两个数相乘,再与第三个数相乘;或者先把后两个数相乘,再与第一个数相乘,它们的积不变。
四 运算律
一、基础练习
同学们经过本单元的学习,你掌握了简便方法计算了吗?试着算一算吧。
101×21=
25×16=
37×25×4=
2121
3700
400
二、指导练习
练习四
1.回答下面的问题,并和同伴说说你是怎么算的。
二、指导练习
观察图中地砖,我们可以怎样分割来进行计算地砖的块数?
算法一
按左面、右面计算
8×12+8×9
=8×(12+9)
=8×21
=168
左面每行8块,共12行。
8×12
前面每行8块,共9行。
8×9
二、指导练习
算法二
按前面、后面计算
16×9+8×3
分别计算前面、后面瓷砖各多少块?然后求和。
列示为:
左面每行16块,共9行。
16×9
前面每行8块,共3行。
8×3
=144+24
=168(块)
二、指导练习
算法三
按添补法计算
16×12-8×3
我们也可以换个思路,先将地砖空白部分补齐,再减去补的地砖数,来求地砖总块数。
列示为:
=192-24
=168(块)
补全后每行16块,共12行。
二、指导练习
168×12
2016>1800
所以准备了1800元不够。
=168×(10+2)
=168×10+168×2
=1680+336
=2016(元)
计算时,将12分成(10+2),利用乘法分配律,计算更简便。
计算地砖所需钱数:
二、指导练习
2.结合下面的例子说一说等式为什么成立。
(3×5)×4=3×(5×4)
3×(5×4)表示
(3×5)×4表示
小正方体的总个数
小正方体的总个数
(3×5)×4=3×(5×4)
不管是先求每层个数,再乘层数,还是先求每排个数,再乘排数,结果都是这些小正方体的总个数,所以所得的结果是一样的。
二、指导练习
2.结合下面的例子说一说等式为什么成立。
3×8+3×6=3×(8+6)
3×(8+6)表示
3×8+3×6表示
碗的总个数
碗的总个数
3×8+3×6=3×(8+6)
不管是先求三个人头上碗的总个数,再加上三个人脚上碗的总个数,还是先求每个人身上碗的总个数,再乘人数,结果都是这些碗的总个数,所以所得的结果是一样的。
二、指导练习
4.
(1)这个花圃的篱笆长多少米?
(30+25)×2=110(米)
求篱笆的长相当于求这个花圃的什么?
周长
答:这个花圃的篱笆长110米。
二、指导练习
4.
(2)如果每平方米大约种40棵郁金香,这个花圃大约种了多少棵郁金香?
30×25=750(m2)
750×40=30000(棵)
答:这个花圃大约种了30000棵郁金香。
关于长方形面积的计算,花圃有多少平方米就有多少个40棵郁金香,从而求出这个花圃大约种了多少棵郁金香。
二、指导练习
5.连一连。
75×2×5
58+147+42
38×29+38
(100+4)×25
38×(29+1)
100×25+4×25
58+42+147
75×(2×5)
三、巩固练习
3.
85×82+82×15
5×289×2
(125×25)×4
25×97+25×3
378+527+73
(125+17)×8
58+39+42+61
76×25+25×24
167+289+33
三、巩固练习
3.
85×82+82×15
=(85+15)×82
5×289×2
=(5×2)×289
(125×25)×4
=125×(25×4)
=8200
=100×82
=10×289
=2890
=125×100
=12500
三、巩固练习
25×97+25×3
=25×(97+3)
378+527+73
=378+(527+73)
(125+17)×8
=125×8+17×8
=1000+136
=1136
=25×100
=2500
=378+600
=978
三、巩固练习
58+39+42+61
=(58+42)+(39+61)
76×25+25×24
=(76+24)×25
167+289+33
=289+(167+33)
=289+200
=489
=100+100
=200
=100×25
=2500
三、巩固练习
6.
(1)列出上述问题的算式,观察每一个算式乘数的变化,你能发现积的变化规律吗?
三、巩固练习
(1)12×2=24(千米)
通过观察得出的结论是:在乘法算式中,一个乘数不变,另一个乘数扩大几倍,积也就相应地扩大几倍。
12×4=48(千米)
12×6=72(千米)
三、巩固练习
(2)利用你发现的规律,能直接写出下列算式的得数吗?
150×20=3000
150×40=
150×60=
360×24=8640
360×12=
360×6=
4320
6000
9000
2160
三、巩固练习
7.(1)5×10-5×3=5×(10-3)成立吗?想办法验证你的想法。
三、巩固练习
由图意可知,一大张蝴蝶图片中共有10竖排,每竖排都有5个蝴蝶图案,可以用10竖排的总数(5×10)减去剪掉的3竖排的数量(5×3),列式为5×10-5×3;还可以先求剩几竖排(10-3),再求剩下的这些竖排有多少个蝴蝶图案,列式为5×(10-3)。因为两个式子求的都是剩下的蝴蝶图案的个数,所以5×10-5×3=5×(10-3)成立。
7.(1)5×10-5×3=5×(10-3)成立吗?想办法验证你的想法。
三、巩固练习
13×99
=13×(100-1)
=13×100-13×1
=1287
(2)你能看懂下面算式的道理吗?
在13×99中,因为99接近100,所以将13×99写成13×(100-1)的形式,运用乘法分配律计算。把算式写成13×100-13×1,即用100个13减去1个13,这样计算更加简便。
三、巩固练习
(3)你能使下面的计算变得简便吗?
206×14-6×14
=(206-6)×14
=200×14
=2800
72×99
=72×(100-1)
=72×100-72×1
=7128
四、课堂小结
两个数相加,交换加数的位置,和不变,叫作加法交换律。
两个数相乘,交换乘数的位置,积不变,叫作乘法交换律。
四、课堂小结
在加法中,三个数相加,先把前两个数相加,再与第三个数相加;或者先把后两个数相加,再与第一个数相加,它们的和不变。
在乘法中,三个数相乘,先把前两个数相乘,再与第三个数相乘;或者先把后两个数相乘,再与第一个数相乘,它们的积不变。
同课章节目录
- 一 认识更大的数
- 1 数一数
- 2 认识更大的数
- 3 人口普查
- 4 国土面积
- 5 近似数
- 6 从结绳计数说起
- 二 线与角
- 1 线的认识
- 2 相交与垂直
- 3 平移与平行
- 4 旋转与角
- 5 角的度量(一)
- 6 角的度量(二)
- 三 乘法
- 1 卫星运行时间
- 2 有多少名观众
- 3 神奇的计算工具
- 4 有趣的算式
- 四 运算律
- 1 买文具
- 2 加法交换律和乘法交换律
- 3 加法结合律
- 4 乘法结合律
- 5 乘法分配律
- 五 方向与位置
- 1 去图书馆
- 2 确定位置
- 六 除法
- 1 买文具
- 2 参观花圃
- 3 秋游
- 4 商不变的规律
- 5 路程、时间与速度
- 七 生活中的负数
- 1 温度
- 2 正负数
- 数学好玩
- 1 滴水试验
- 2 编码
- 3 数图形的学问
- 八 可能性
- 1 不确定性
- 2 摸球游戏
