1.2空间几何体的三视图和直观图
图片预览




文档简介
(共55张PPT)
空间几何体的三视图和直观图
1.2
主要内容
1.2.2空间几何体的三视图
1.2.3空间几何体的直观图
1.2.1 中心投影与平行投影
中心投影与平行投影
1.2.1
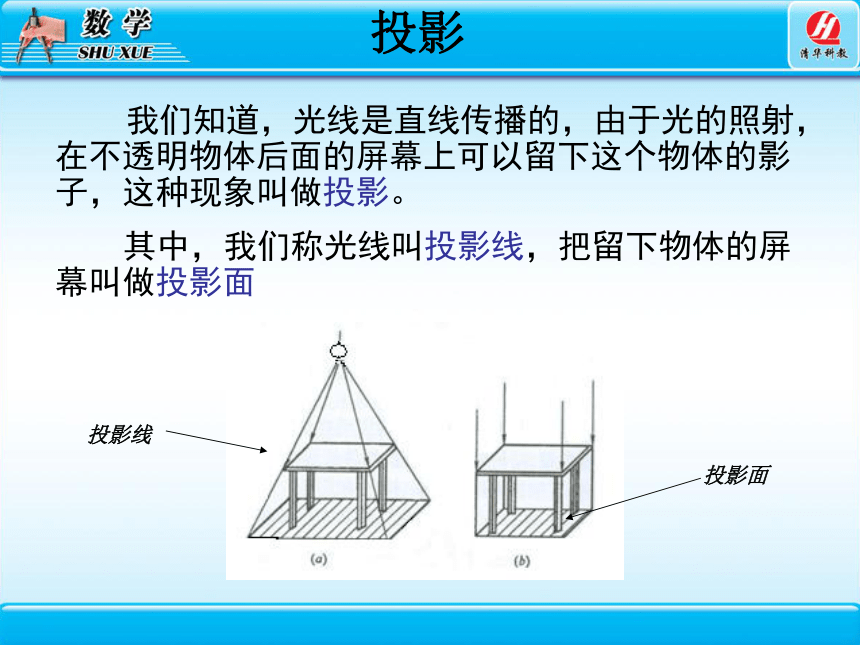
投影
我们知道,光线是直线传播的,由于光的照射,在不透明物体后面的屏幕上可以留下这个物体的影子,这种现象叫做投影。
其中,我们称光线叫投影线,把留下物体的屏幕叫做投影面
投影面
投影线
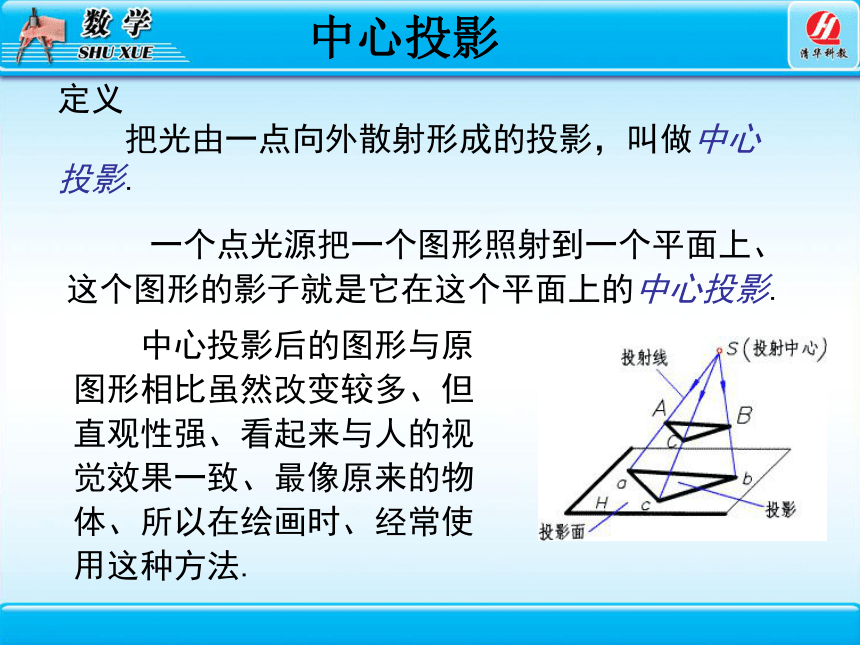
中心投影
定义
把光由一点向外散射形成的投影,叫做中心
投影.
一个点光源把一个图形照射到一个平面上、这个图形的影子就是它在这个平面上的中心投影.
中心投影后的图形与原图形相比虽然改变较多、但直观性强、看起来与人的视觉效果一致、最像原来的物体、所以在绘画时、经常使用这种方法.
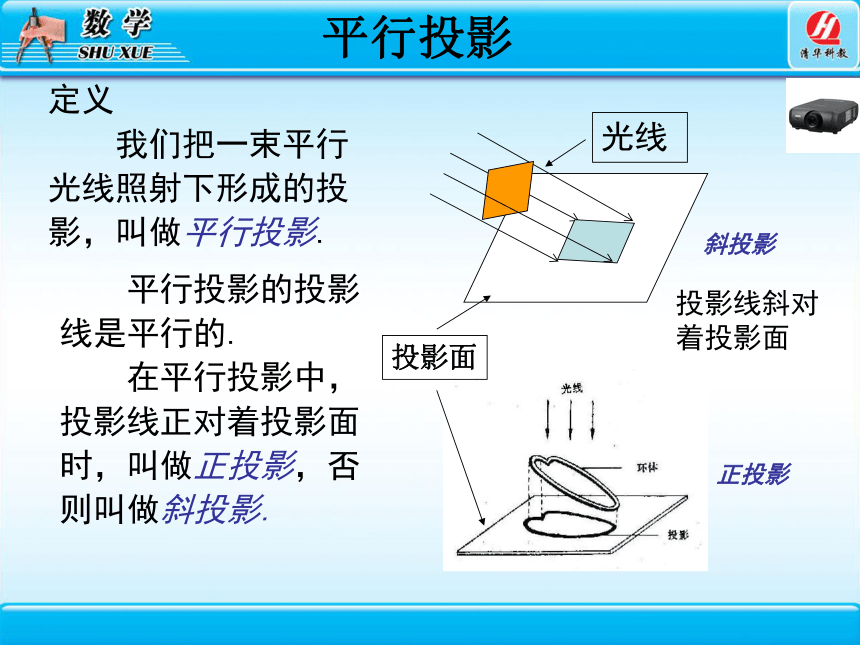
平行投影
定义
我们把一束平行光线照射下形成的投影,叫做平行投影.
平行投影的投影线是平行的.
在平行投影中,投影线正对着投影面时,叫做正投影,否则叫做斜投影.
斜投影
正投影
投影线斜对着投影面
投影面
光线
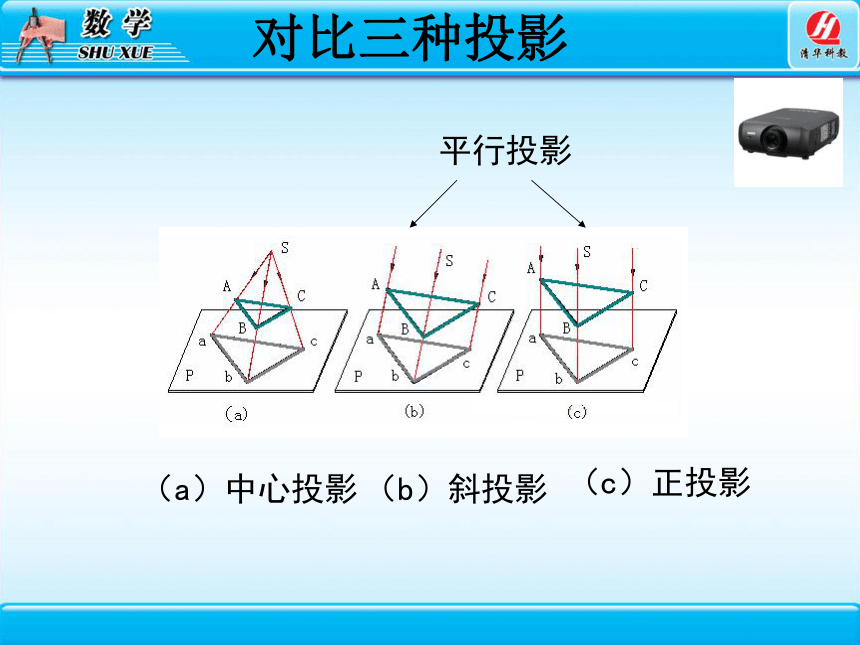
对比三种投影
(a)中心投影
(b)斜投影
(c)正投影
平行投影
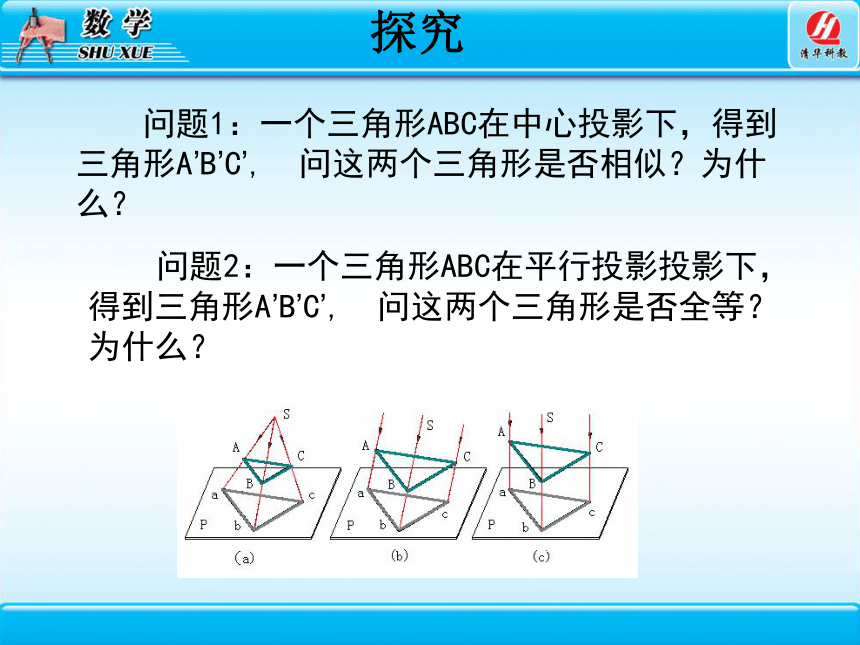
探究
问题1:一个三角形ABC在中心投影下,得到三角形A’B’C’, 问这两个三角形是否相似?为什么?
问题2:一个三角形ABC在平行投影投影下,得到三角形A’B’C’, 问这两个三角形是否全等?为什么?
小结
投影
中心投影
平行投影
空间几何体的三视图
1.2.2
基本几何体的三视图
回忆初中已经学过的正方体、长方体、圆柱、圆锥、球的三视图.
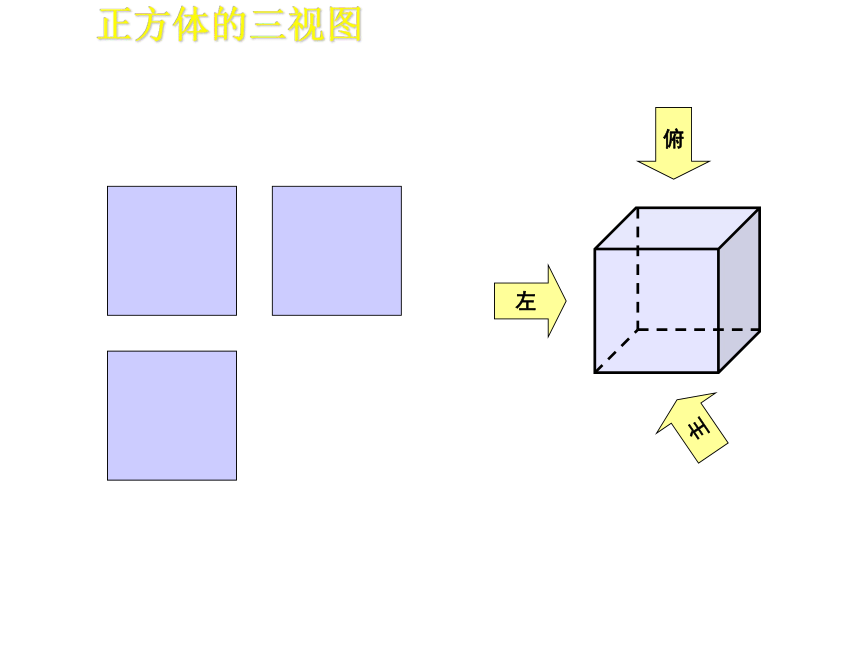
正方体的三视图
主
左
俯
长方体
主
左
俯
长方体的三视图
圆柱
主
左
俯
圆柱的三视图
圆锥
主
左
俯
圆锥的三视图
球体
主
左
俯
球的三视图
三个互相垂直的投影面
“视图”是将物体按正投影法向投影面投射时所得到的投影图.
从左向右方向的投影线
从上到下方向的投影线
从前向后方向的投影线
三视图概念
三视图的形成
正视图
侧视图
俯视图
光线从几何体的上面向下面正投影所得的投影图称为“俯视图”.
光线从几何体的前面向后面正投影所得的投影图称为“正视图”
光线从几何体的左面向右面正投影所得的投影图称为“侧视图”
三视图的平面位置
正视图
侧视图
俯视图
正视图、侧视图、俯视图在平面图中的一般位置
正视图、侧视图、俯视图统称为三视图
三视图的关系
结论:
1.一个几何体的正视图和侧视图的高度一样,
2.正视图与俯视图的长度一样
3.侧视图与俯视图宽度一样
正视图
侧视图
俯视图
定义:长、宽、高
长
宽
宽相等
长对正
高平齐
长:左、右方向的长度
宽:前、后方向的长度
高:上、下方向的长度
基本几何体三视图
上一节学习的棱柱、棱锥、棱台以及圆台的三视图是怎样的?
正三棱锥
主
左
俯
棱锥的三视图
棱锥的三视图
正四棱锥
主
左
俯
举例画出三视图
圆锥
正视图
侧视图
俯视图
正三棱锥
正视图
侧视图
俯视图
举例画出三视图
举例画出三视图
六棱柱
正视图
侧视图
俯视图
举例画出三视图
根据三视图想象其表示的几何体
根据三视图想象它们表示的几何体的结构特征
圆台
俯视图
正视图
侧视图
根据三视图想象它们表示的几何体的结构特征
正四棱台
正视图
侧视图
俯视图
简单组合体的三视图
下面是一些立体图形的三视图,请根据视图说出立体图形的名称:
正视图
侧视图
俯视图
四棱柱
由三视图想象几何体
下面是一些立体图形的三视图,请根据视图说出立体图形的名称:
正视图
左视图
俯视图
圆锥
由三视图想象几何体
四棱锥
一个几何体的三视图如下,你能说出它是什么立体图形吗
由三视图想象几何体
A
F
D
B
A
C
E
C
D
一个正方体各面分别标上A、B、C、D、E、F,甲、乙、丙三位同学从不同的方向观察正方体,结果如下图,则各面的字母分别是什么?
知识小结
小结
三视图的概念
三视图的形成
三视图的平面位置
三视图的关系
三视图的举例
简单组合体的三视图
作业
P15 练习1,2,3,4
P20-21 习题1.2 1,2,3.
1.2.3 空间几何体的直观图
空间几何体的直观图
1.2.3
斜二测画法
问:正方体的每个面都是正方形,但在平面图中有几个面画成正方形?平行四边形?
观察正方体的平面图
正方形的水平直观图
x
y
x
y
水平直观图
1. 水平方向线段长度不变;
2. 竖直方向的线段向右倾斜450,长度减半;
3. 平行线段仍然平行.
变化规则
0
0
水平直观图
正三角形的水平直观图
A
B
C
M
B
C
A
y
o
x
0
水平直观图
直角梯形的水平直观图
x′
y′
C′
x
y
A′
B′
D′
A
B
C
D
A
B
C
D
E
F
M
N
x′
y′
o′
B′
C′
A′
D′
E′
F′
M
N
x
y
正六边形的水平直观图的画法
水平直观图
斜二测画法
定义:上述画水平放置的平面图形的直观图的方法叫做斜二测画法,有如下步骤和规则
(3)水平线段等长,竖直线段减半.
(2)与坐标轴平行的线段保持平行;
(1)在原图形中建立平面直角坐标系xoy,同时建立直观图坐标系 ,确定水平面,
x'
y'
o
x
y
0
空间几何体的直观图
例1.画长、宽、高分别为4cm、3cm、2cm的长方体ABCD-A′B′C′D′的直观图?
A
B
C
D
z
A′
B′
C′
D′
x
y
o
P
Q
A′
B′
C′
D′
A
B
C
D
水平方向的矩形画成平行四边形的直观图竖直方向(z轴)的线段长度不变
斜二测画法
侧视图
俯视图
正视图
z
A
B
o′
A′
B′
o
x
y
x′
y′
由几何体的三视图可以得到几何体的直观图
反思提高
思考题:如图ΔA’B’C’是水平放置的ΔABC的直观图,则在ΔABC的三边及中线AD中,最长的线段是( )
小结
正方形的水平直观图
正三角形的水平直观图
直角梯形的水平直观图
正六边形的水平直观图
斜二测画法
长方体的直观图
作业
P19-20 练习 1,2,3,4,5
P21 习题1.2 A.4,5 B组1,2,3
空间几何体的三视图和直观图
1.2
主要内容
1.2.2空间几何体的三视图
1.2.3空间几何体的直观图
1.2.1 中心投影与平行投影
中心投影与平行投影
1.2.1
投影
我们知道,光线是直线传播的,由于光的照射,在不透明物体后面的屏幕上可以留下这个物体的影子,这种现象叫做投影。
其中,我们称光线叫投影线,把留下物体的屏幕叫做投影面
投影面
投影线
中心投影
定义
把光由一点向外散射形成的投影,叫做中心
投影.
一个点光源把一个图形照射到一个平面上、这个图形的影子就是它在这个平面上的中心投影.
中心投影后的图形与原图形相比虽然改变较多、但直观性强、看起来与人的视觉效果一致、最像原来的物体、所以在绘画时、经常使用这种方法.
平行投影
定义
我们把一束平行光线照射下形成的投影,叫做平行投影.
平行投影的投影线是平行的.
在平行投影中,投影线正对着投影面时,叫做正投影,否则叫做斜投影.
斜投影
正投影
投影线斜对着投影面
投影面
光线
对比三种投影
(a)中心投影
(b)斜投影
(c)正投影
平行投影
探究
问题1:一个三角形ABC在中心投影下,得到三角形A’B’C’, 问这两个三角形是否相似?为什么?
问题2:一个三角形ABC在平行投影投影下,得到三角形A’B’C’, 问这两个三角形是否全等?为什么?
小结
投影
中心投影
平行投影
空间几何体的三视图
1.2.2
基本几何体的三视图
回忆初中已经学过的正方体、长方体、圆柱、圆锥、球的三视图.
正方体的三视图
主
左
俯
长方体
主
左
俯
长方体的三视图
圆柱
主
左
俯
圆柱的三视图
圆锥
主
左
俯
圆锥的三视图
球体
主
左
俯
球的三视图
三个互相垂直的投影面
“视图”是将物体按正投影法向投影面投射时所得到的投影图.
从左向右方向的投影线
从上到下方向的投影线
从前向后方向的投影线
三视图概念
三视图的形成
正视图
侧视图
俯视图
光线从几何体的上面向下面正投影所得的投影图称为“俯视图”.
光线从几何体的前面向后面正投影所得的投影图称为“正视图”
光线从几何体的左面向右面正投影所得的投影图称为“侧视图”
三视图的平面位置
正视图
侧视图
俯视图
正视图、侧视图、俯视图在平面图中的一般位置
正视图、侧视图、俯视图统称为三视图
三视图的关系
结论:
1.一个几何体的正视图和侧视图的高度一样,
2.正视图与俯视图的长度一样
3.侧视图与俯视图宽度一样
正视图
侧视图
俯视图
定义:长、宽、高
长
宽
宽相等
长对正
高平齐
长:左、右方向的长度
宽:前、后方向的长度
高:上、下方向的长度
基本几何体三视图
上一节学习的棱柱、棱锥、棱台以及圆台的三视图是怎样的?
正三棱锥
主
左
俯
棱锥的三视图
棱锥的三视图
正四棱锥
主
左
俯
举例画出三视图
圆锥
正视图
侧视图
俯视图
正三棱锥
正视图
侧视图
俯视图
举例画出三视图
举例画出三视图
六棱柱
正视图
侧视图
俯视图
举例画出三视图
根据三视图想象其表示的几何体
根据三视图想象它们表示的几何体的结构特征
圆台
俯视图
正视图
侧视图
根据三视图想象它们表示的几何体的结构特征
正四棱台
正视图
侧视图
俯视图
简单组合体的三视图
下面是一些立体图形的三视图,请根据视图说出立体图形的名称:
正视图
侧视图
俯视图
四棱柱
由三视图想象几何体
下面是一些立体图形的三视图,请根据视图说出立体图形的名称:
正视图
左视图
俯视图
圆锥
由三视图想象几何体
四棱锥
一个几何体的三视图如下,你能说出它是什么立体图形吗
由三视图想象几何体
A
F
D
B
A
C
E
C
D
一个正方体各面分别标上A、B、C、D、E、F,甲、乙、丙三位同学从不同的方向观察正方体,结果如下图,则各面的字母分别是什么?
知识小结
小结
三视图的概念
三视图的形成
三视图的平面位置
三视图的关系
三视图的举例
简单组合体的三视图
作业
P15 练习1,2,3,4
P20-21 习题1.2 1,2,3.
1.2.3 空间几何体的直观图
空间几何体的直观图
1.2.3
斜二测画法
问:正方体的每个面都是正方形,但在平面图中有几个面画成正方形?平行四边形?
观察正方体的平面图
正方形的水平直观图
x
y
x
y
水平直观图
1. 水平方向线段长度不变;
2. 竖直方向的线段向右倾斜450,长度减半;
3. 平行线段仍然平行.
变化规则
0
0
水平直观图
正三角形的水平直观图
A
B
C
M
B
C
A
y
o
x
0
水平直观图
直角梯形的水平直观图
x′
y′
C′
x
y
A′
B′
D′
A
B
C
D
A
B
C
D
E
F
M
N
x′
y′
o′
B′
C′
A′
D′
E′
F′
M
N
x
y
正六边形的水平直观图的画法
水平直观图
斜二测画法
定义:上述画水平放置的平面图形的直观图的方法叫做斜二测画法,有如下步骤和规则
(3)水平线段等长,竖直线段减半.
(2)与坐标轴平行的线段保持平行;
(1)在原图形中建立平面直角坐标系xoy,同时建立直观图坐标系 ,确定水平面,
x'
y'
o
x
y
0
空间几何体的直观图
例1.画长、宽、高分别为4cm、3cm、2cm的长方体ABCD-A′B′C′D′的直观图?
A
B
C
D
z
A′
B′
C′
D′
x
y
o
P
Q
A′
B′
C′
D′
A
B
C
D
水平方向的矩形画成平行四边形的直观图竖直方向(z轴)的线段长度不变
斜二测画法
侧视图
俯视图
正视图
z
A
B
o′
A′
B′
o
x
y
x′
y′
由几何体的三视图可以得到几何体的直观图
反思提高
思考题:如图ΔA’B’C’是水平放置的ΔABC的直观图,则在ΔABC的三边及中线AD中,最长的线段是( )
小结
正方形的水平直观图
正三角形的水平直观图
直角梯形的水平直观图
正六边形的水平直观图
斜二测画法
长方体的直观图
作业
P19-20 练习 1,2,3,4,5
P21 习题1.2 A.4,5 B组1,2,3
