2.2直线、平面平行的判定及其性质(新课标A版)
文档属性
| 名称 | 2.2直线、平面平行的判定及其性质(新课标A版) |  | |
| 格式 | zip | ||
| 文件大小 | 735.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-03-29 17:41:46 | ||
图片预览




文档简介
(共52张PPT)
直线、平面平行的
判定及其性质
2.2
主要内容
2.2.2 平面与平面平行的判定
2.2.3 直线与平面平行的性质
2.2.1 直线与平面平行的判定
2.2.4 平面与平面平行的性质
直线与平面平行的
判定
2.2.1
(1)直线在平面内——有无数个公共点.
(2)直线和平面相交——有且只有一个公共点.
(3)直线和平面平行——无公共点.
一条直线和一个平面的位置关系有且只有以下三种:
直线和平面相交或平行的情况统称为直线在平面外.
直线和平面的位置关系
复习
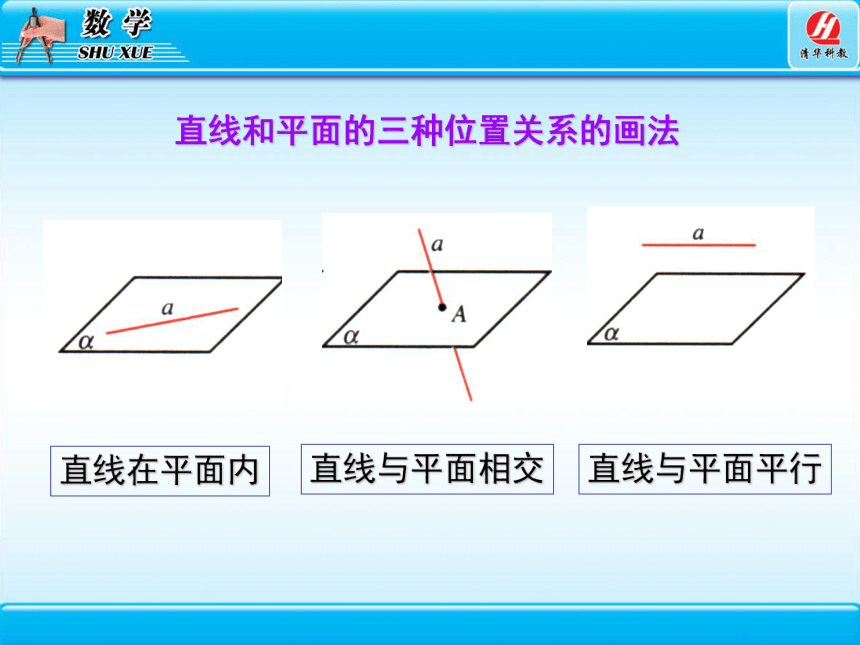
直线和平面的三种位置关系的画法
直线在平面内
直线与平面相交
直线与平面平行
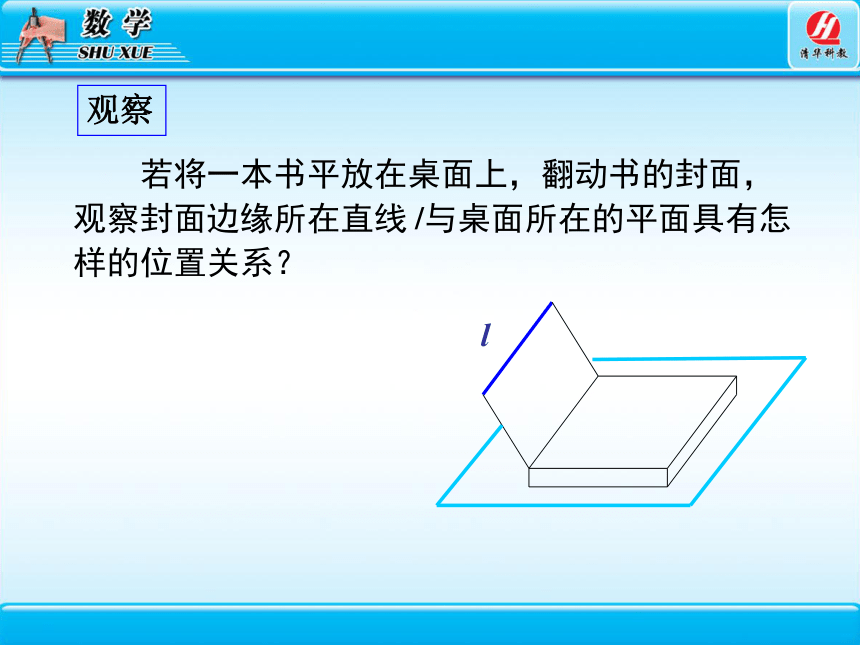
若将一本书平放在桌面上,翻动书的封面,观察封面边缘所在直线l与桌面所在的平面具有怎样的位置关系?
观察
l
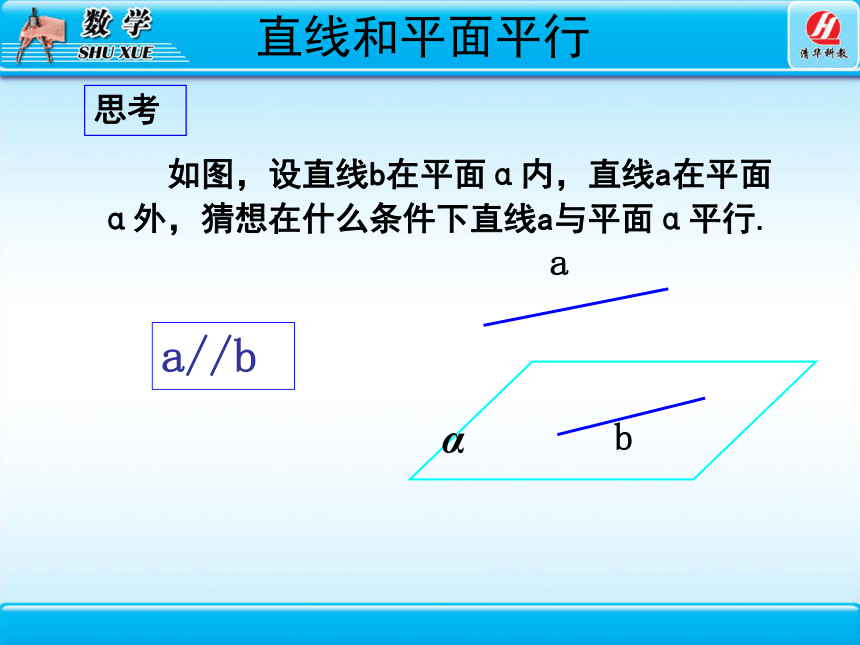
如图,设直线b在平面α内,直线a在平面α外,猜想在什么条件下直线a与平面α平行.
b
a
α
a//b
思考
直线和平面平行
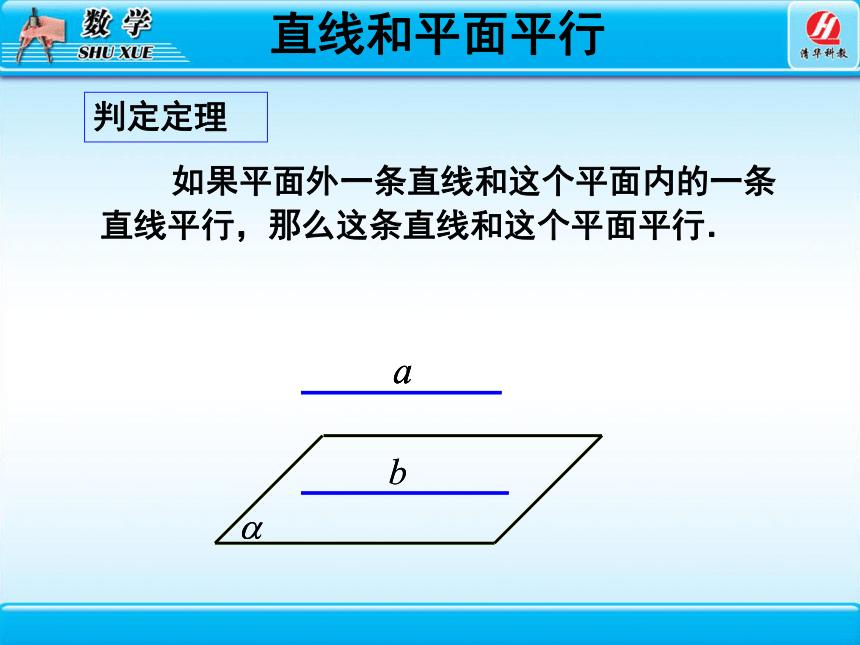
直线和平面平行
如果平面外一条直线和这个平面内的一条直线平行,那么这条直线和这个平面平行.
判定定理
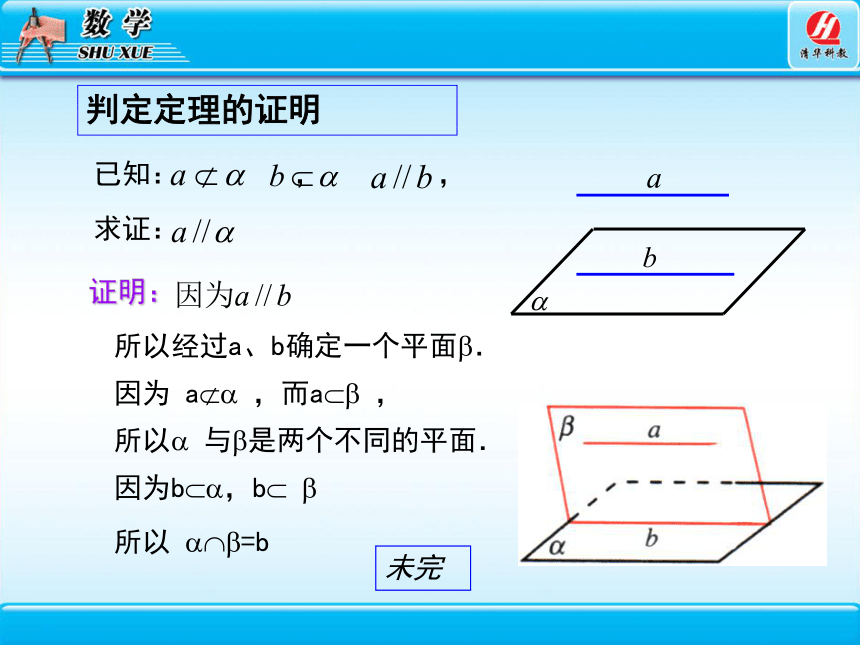
判定定理的证明
已知: , ,
求证:
证明:
所以经过a、b确定一个平面 .
因为 a ,而a ,
所以 与 是两个不同的平面.
所以 =b
未完
因为b ,b
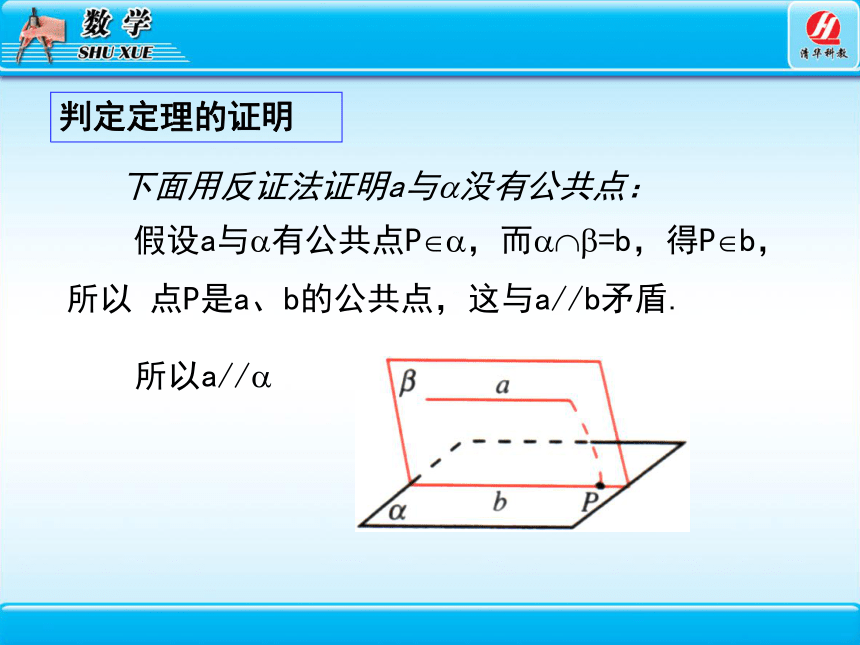
下面用反证法证明a与 没有公共点:
判定定理的证明
假设a与 有公共点P ,而 =b,得P b,
所以 点P是a、b的公共点,这与a//b矛盾.
所以a//
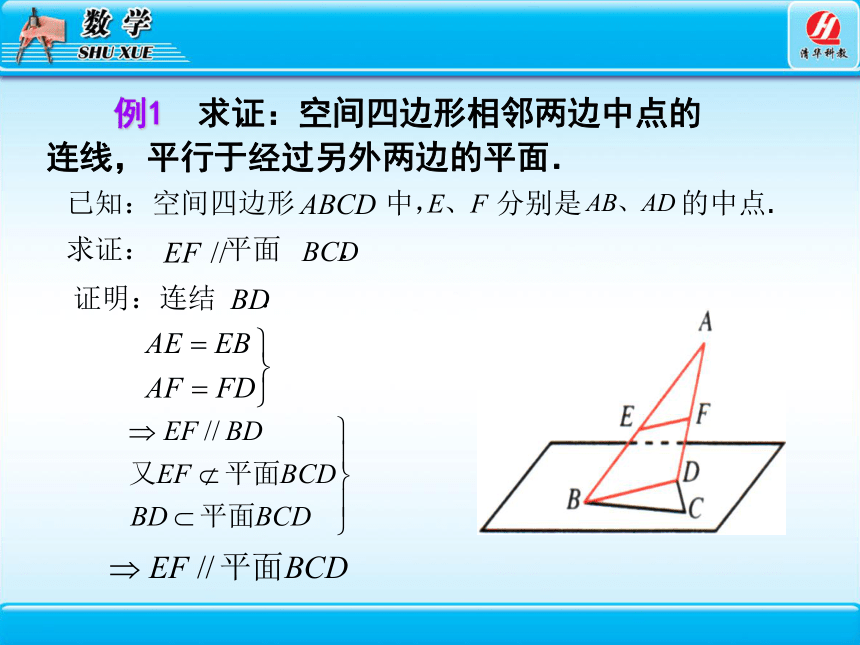
例1 求证:空间四边形相邻两边中点的连线,平行于经过另外两边的平面.
已知:空间四边形 中, 分别是 的中点.
求证: 平面 .
证明:连结 .
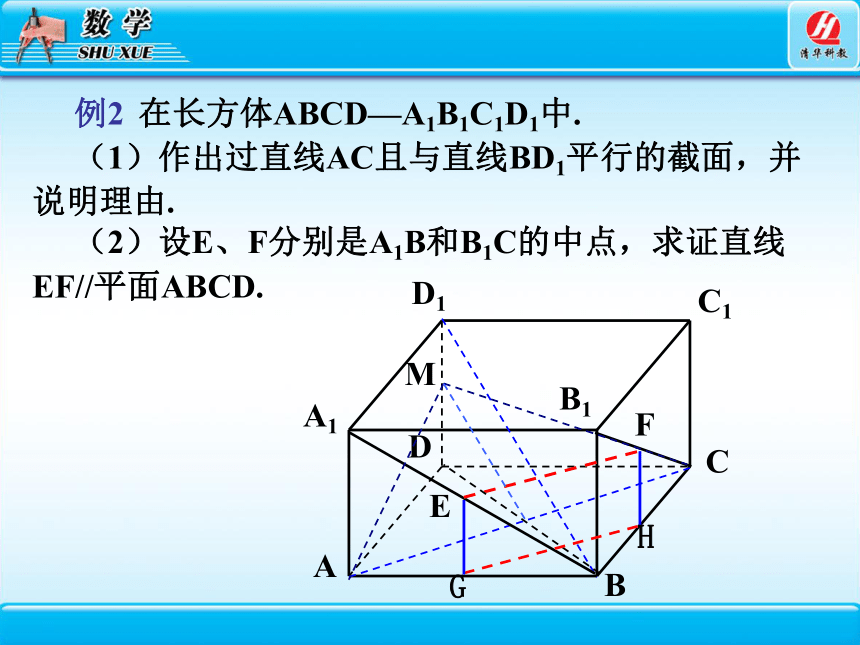
例2 在长方体ABCD—A1B1C1D1中.
(1)作出过直线AC且与直线BD1平行的截面,并说明理由.
A
B
C
C1
D
A1
B1
D1
E
F
M
G
H
(2)设E、F分别是A1B和B1C的中点,求证直线EF//平面ABCD.
直线与平面平行的判定定理可简述为
“线线平行,则线面平行”
小结
通过直线间的平行,推证直线与平面平
行,即将直线与平面的平行关系(空间问题)转化为直线间的平行关系(平面问题).
思想方法
作业
P55-56练习1,2
P62 习题2.2 A组 3,4
平面与平面平行的判定
2.2.2
思考1:
我们知道,两个平面的位置关系是平行或相交.
问:对于两个平面α、β,你猜想在什么条件下可保证平面α与平面β平行?
1.三角板的一条边所在直线与桌面平行,这个三角板所在平面与桌面平行吗?
A
2. 三角板的两条边所在直线分别与桌面平行,三角板所在平面与桌面平行吗?
A
思考2
1.一般地,如果平面α内有一条直线平行于平面β,那么平面α与平面β一定平行吗?
2. 如果平面α内有两条直线平行于平面β,那么平面α与平面β一定平行吗?
思考3
α
β
两个平面平行的判定
判定定理:如果一个平面内有两条相交直线都平行于另一个平面,那么这两个平面平行.
平面平行的判定定理的证明
已知:在平面 内,有两条直线 、 相交且和平面 平行.
求证: .
证明:用反证法证明.
假设 .
同理
这与题设 和 是相交直线是矛盾的.
例1 已知:在正方体ABCD-A′B′C′D′中.
求证:平面AB′D′∥平面BC′D.
B
A
A′
B′
C′
D′
C
D
例题分析
例2 在三棱锥P-ABC中,点D、E、F分别是△PAB、△PBC、△PAC的重心.
求证:平面DEF//平面ABC.
P
A
B
C
D
E
F
M
N
直线
交与点
求证:平面 平面
练习
已知:
小结
1. 知识小结
2. 思想方法
面面平行
线线平行
线面平行
作业
P58练习1,2,3
P62 习题2.2 A组 7,8
直线与平面平行的
性质
2.2.3
直线与平面平行的判定定理是什么?
复习
定理 若平面外一条直线与此平面内的
一条直线平行,则该直线与此平面平行.
问:其逆定理是否成立?
如果直线a与平面α平行,那么直线a与平面α内的直线有哪些位置关系?
思考1
a
α
若直线a与平面α平行,那么在平面α内与直线a平行的直线有多少条?这些直线的位置关系如何?
a
α
思考2
教室内日光灯管所在的直线与地面平行,如何在地面上作一条直线与灯管所在的直线平行?
思考3
a
α
性质定理及证明
如果一条直线和一个平面平行,经过这条直线的平面和这个平面相交,那么这条直线和交线平行.
已知: , ,
求证: .
证明: .
直线与平面平行
教室内日光灯管所在的直线与地面平行,如何在地面上作一条直线与灯管所在的直线平行?
问题解决
灯管
地面
例1 在图中所示的一块木料中,棱BC平行于平面A’C’ .
(1)要经过平面 内的一点P 和棱BC将木料据开,应怎样画线?
(2)所画的线和平面AC 是什么位置关系?
A
A′
C
B
D
P
D′
B′
C′
例2 已知平面外的两条平行直线中的一条平行于这个平面,求证另一条也平行于这个平面.
c
a
b
α
如图,已知直线a,b和平面α ,a∥b,a∥α , a,b都在平面α外 .
求证:b∥α .
练习
如果三个平面两两相交,有三条交线,如果有两条交线平行,那么第三条交线和这两条交线的位置关系如何?
α
β
a
b
l
三条交线两两平行
小结
直线与平面平行的性质定理可简述为
“线面平行,则线线平行”
思想方法
线面平行的性质定理不但提供了用线面平行来证明线线平行的方法,也提供了作平行线的一种方法.
作业
P61-63习题2.2 A组1,2,5,6
平面与平面平行的性质
2.2.4
复习1:
两个平面的位置关系是 .
平行或相交
两个平面平行的判定
判定定理:如果一个平面内有两条相交直线都平行于另一个平面,那么这两个平面平行.
复习2:
若 ,则直线l与平面β的位置关系如何?
思考1
两个平面平行的性质
结论1
如果两个平面平行,那么其中一个平面内的直线平行于另一个平面.
若 ,直线 l 与平面α相交,那么直线 l 与平面β的位置关系如何?
思考2
β
α
l
β
α
若 // ,平面α、β分别与平面γ相交于直线a、b,那么直线a、b的位置关系如何?为什么?
思考3
a
b
两个平面平行的性质定理
定理:如果两个平行平面同时和第三个平面相交,那么它们的交线平行.
即:
这个定理判定两直线平行的依据之一
例1 求证:夹在两个平行平面间的平行线段相等.
D
α
B
β
A
C
例2 在正方体ABCD-A′B′C′D′中,点M在CD′上,试判断直线MB′与平面BDA′的位置关系,并说明理由.
A′
B′
C′
D′
A
B
C
D
M
例3 如图,已知AB、CD是夹在两个平行平面α、β之间的线段,M、N分别为AB、CD的中点,求证:MN∥平面β.
A
B
C
D
α
M
N
β
E
l
练习1
α
β
γ
a
b
l
b
α
β
γ
a
l
相交于一条交线
三条交线两两平行
三条交线相交于一点
如果三个平面两两相交,那么它们的交线位置如何?
一条斜线和两个平行平面相交,求证它和两个平面所成的角相等.
应用举例
练习2
小结
知识小结
几个结论和性质的应用
思想方法
线面平行或线线平行
面面平行
作业
P61 练习
P63习题2.2 B组2,3,4
直线、平面平行的
判定及其性质
2.2
主要内容
2.2.2 平面与平面平行的判定
2.2.3 直线与平面平行的性质
2.2.1 直线与平面平行的判定
2.2.4 平面与平面平行的性质
直线与平面平行的
判定
2.2.1
(1)直线在平面内——有无数个公共点.
(2)直线和平面相交——有且只有一个公共点.
(3)直线和平面平行——无公共点.
一条直线和一个平面的位置关系有且只有以下三种:
直线和平面相交或平行的情况统称为直线在平面外.
直线和平面的位置关系
复习
直线和平面的三种位置关系的画法
直线在平面内
直线与平面相交
直线与平面平行
若将一本书平放在桌面上,翻动书的封面,观察封面边缘所在直线l与桌面所在的平面具有怎样的位置关系?
观察
l
如图,设直线b在平面α内,直线a在平面α外,猜想在什么条件下直线a与平面α平行.
b
a
α
a//b
思考
直线和平面平行
直线和平面平行
如果平面外一条直线和这个平面内的一条直线平行,那么这条直线和这个平面平行.
判定定理
判定定理的证明
已知: , ,
求证:
证明:
所以经过a、b确定一个平面 .
因为 a ,而a ,
所以 与 是两个不同的平面.
所以 =b
未完
因为b ,b
下面用反证法证明a与 没有公共点:
判定定理的证明
假设a与 有公共点P ,而 =b,得P b,
所以 点P是a、b的公共点,这与a//b矛盾.
所以a//
例1 求证:空间四边形相邻两边中点的连线,平行于经过另外两边的平面.
已知:空间四边形 中, 分别是 的中点.
求证: 平面 .
证明:连结 .
例2 在长方体ABCD—A1B1C1D1中.
(1)作出过直线AC且与直线BD1平行的截面,并说明理由.
A
B
C
C1
D
A1
B1
D1
E
F
M
G
H
(2)设E、F分别是A1B和B1C的中点,求证直线EF//平面ABCD.
直线与平面平行的判定定理可简述为
“线线平行,则线面平行”
小结
通过直线间的平行,推证直线与平面平
行,即将直线与平面的平行关系(空间问题)转化为直线间的平行关系(平面问题).
思想方法
作业
P55-56练习1,2
P62 习题2.2 A组 3,4
平面与平面平行的判定
2.2.2
思考1:
我们知道,两个平面的位置关系是平行或相交.
问:对于两个平面α、β,你猜想在什么条件下可保证平面α与平面β平行?
1.三角板的一条边所在直线与桌面平行,这个三角板所在平面与桌面平行吗?
A
2. 三角板的两条边所在直线分别与桌面平行,三角板所在平面与桌面平行吗?
A
思考2
1.一般地,如果平面α内有一条直线平行于平面β,那么平面α与平面β一定平行吗?
2. 如果平面α内有两条直线平行于平面β,那么平面α与平面β一定平行吗?
思考3
α
β
两个平面平行的判定
判定定理:如果一个平面内有两条相交直线都平行于另一个平面,那么这两个平面平行.
平面平行的判定定理的证明
已知:在平面 内,有两条直线 、 相交且和平面 平行.
求证: .
证明:用反证法证明.
假设 .
同理
这与题设 和 是相交直线是矛盾的.
例1 已知:在正方体ABCD-A′B′C′D′中.
求证:平面AB′D′∥平面BC′D.
B
A
A′
B′
C′
D′
C
D
例题分析
例2 在三棱锥P-ABC中,点D、E、F分别是△PAB、△PBC、△PAC的重心.
求证:平面DEF//平面ABC.
P
A
B
C
D
E
F
M
N
直线
交与点
求证:平面 平面
练习
已知:
小结
1. 知识小结
2. 思想方法
面面平行
线线平行
线面平行
作业
P58练习1,2,3
P62 习题2.2 A组 7,8
直线与平面平行的
性质
2.2.3
直线与平面平行的判定定理是什么?
复习
定理 若平面外一条直线与此平面内的
一条直线平行,则该直线与此平面平行.
问:其逆定理是否成立?
如果直线a与平面α平行,那么直线a与平面α内的直线有哪些位置关系?
思考1
a
α
若直线a与平面α平行,那么在平面α内与直线a平行的直线有多少条?这些直线的位置关系如何?
a
α
思考2
教室内日光灯管所在的直线与地面平行,如何在地面上作一条直线与灯管所在的直线平行?
思考3
a
α
性质定理及证明
如果一条直线和一个平面平行,经过这条直线的平面和这个平面相交,那么这条直线和交线平行.
已知: , ,
求证: .
证明: .
直线与平面平行
教室内日光灯管所在的直线与地面平行,如何在地面上作一条直线与灯管所在的直线平行?
问题解决
灯管
地面
例1 在图中所示的一块木料中,棱BC平行于平面A’C’ .
(1)要经过平面 内的一点P 和棱BC将木料据开,应怎样画线?
(2)所画的线和平面AC 是什么位置关系?
A
A′
C
B
D
P
D′
B′
C′
例2 已知平面外的两条平行直线中的一条平行于这个平面,求证另一条也平行于这个平面.
c
a
b
α
如图,已知直线a,b和平面α ,a∥b,a∥α , a,b都在平面α外 .
求证:b∥α .
练习
如果三个平面两两相交,有三条交线,如果有两条交线平行,那么第三条交线和这两条交线的位置关系如何?
α
β
a
b
l
三条交线两两平行
小结
直线与平面平行的性质定理可简述为
“线面平行,则线线平行”
思想方法
线面平行的性质定理不但提供了用线面平行来证明线线平行的方法,也提供了作平行线的一种方法.
作业
P61-63习题2.2 A组1,2,5,6
平面与平面平行的性质
2.2.4
复习1:
两个平面的位置关系是 .
平行或相交
两个平面平行的判定
判定定理:如果一个平面内有两条相交直线都平行于另一个平面,那么这两个平面平行.
复习2:
若 ,则直线l与平面β的位置关系如何?
思考1
两个平面平行的性质
结论1
如果两个平面平行,那么其中一个平面内的直线平行于另一个平面.
若 ,直线 l 与平面α相交,那么直线 l 与平面β的位置关系如何?
思考2
β
α
l
β
α
若 // ,平面α、β分别与平面γ相交于直线a、b,那么直线a、b的位置关系如何?为什么?
思考3
a
b
两个平面平行的性质定理
定理:如果两个平行平面同时和第三个平面相交,那么它们的交线平行.
即:
这个定理判定两直线平行的依据之一
例1 求证:夹在两个平行平面间的平行线段相等.
D
α
B
β
A
C
例2 在正方体ABCD-A′B′C′D′中,点M在CD′上,试判断直线MB′与平面BDA′的位置关系,并说明理由.
A′
B′
C′
D′
A
B
C
D
M
例3 如图,已知AB、CD是夹在两个平行平面α、β之间的线段,M、N分别为AB、CD的中点,求证:MN∥平面β.
A
B
C
D
α
M
N
β
E
l
练习1
α
β
γ
a
b
l
b
α
β
γ
a
l
相交于一条交线
三条交线两两平行
三条交线相交于一点
如果三个平面两两相交,那么它们的交线位置如何?
一条斜线和两个平行平面相交,求证它和两个平面所成的角相等.
应用举例
练习2
小结
知识小结
几个结论和性质的应用
思想方法
线面平行或线线平行
面面平行
作业
P61 练习
P63习题2.2 B组2,3,4
