1.3空间几何体的表面积和体积
文档属性
| 名称 | 1.3空间几何体的表面积和体积 |  | |
| 格式 | zip | ||
| 文件大小 | 566.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-03-29 17:43:13 | ||
图片预览



文档简介
(共29张PPT)
空间几何体的表面积与体积
1.3
主要内容
1.3.2 球的表面积和体积
1.3.1 柱体、椎体、台体的表面积与体积
1.3.1
柱体、锥体、台体的表面积与体积
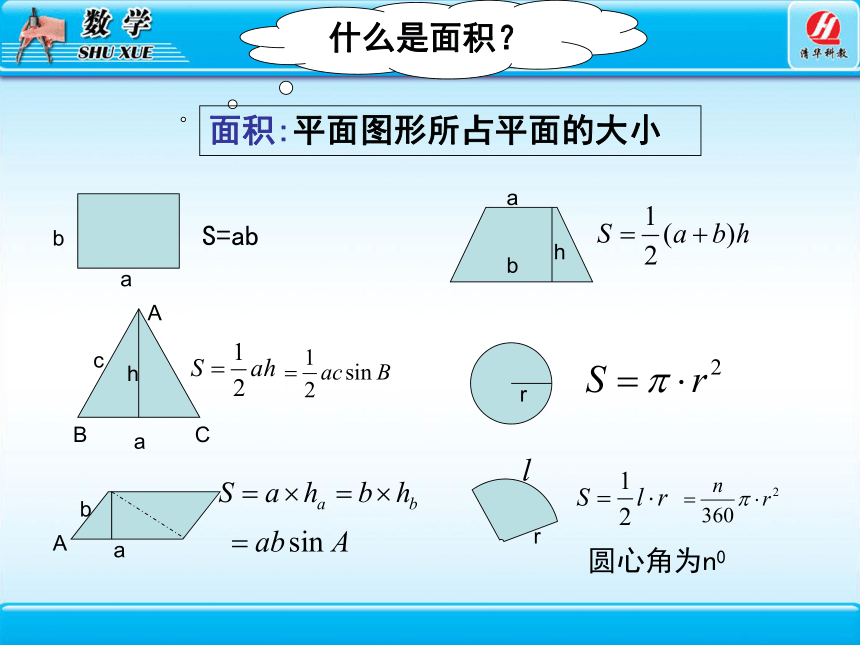
什么是面积?
面积:平面图形所占平面的大小
S=ab
a
b
A
a
h
B
C
a
b
h
a
b
A
r
圆心角为n0
r
c
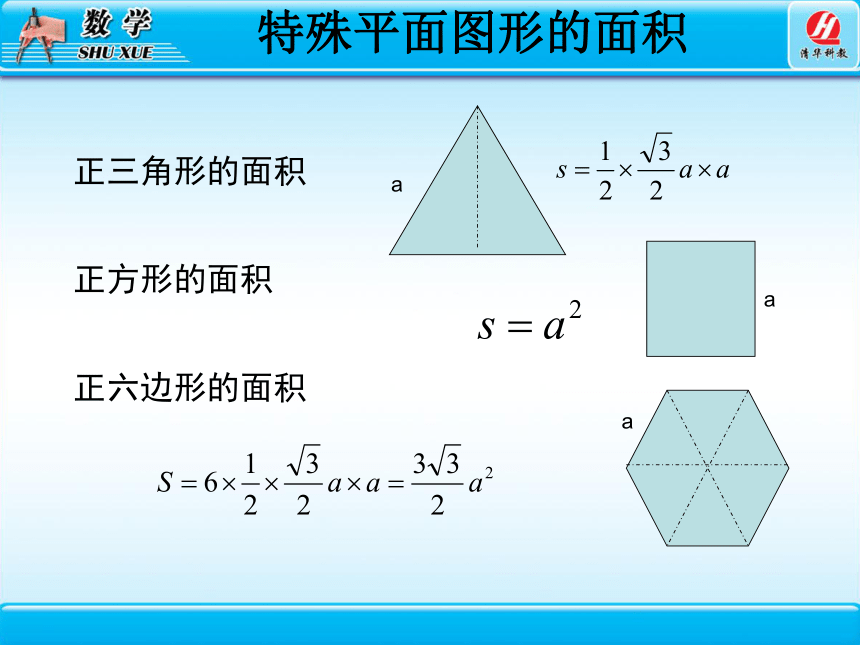
特殊平面图形的面积
正三角形的面积
正六边形的面积
正方形的面积
a
a
a
设长方体的长宽高分别为a、b、h,则其表面积为
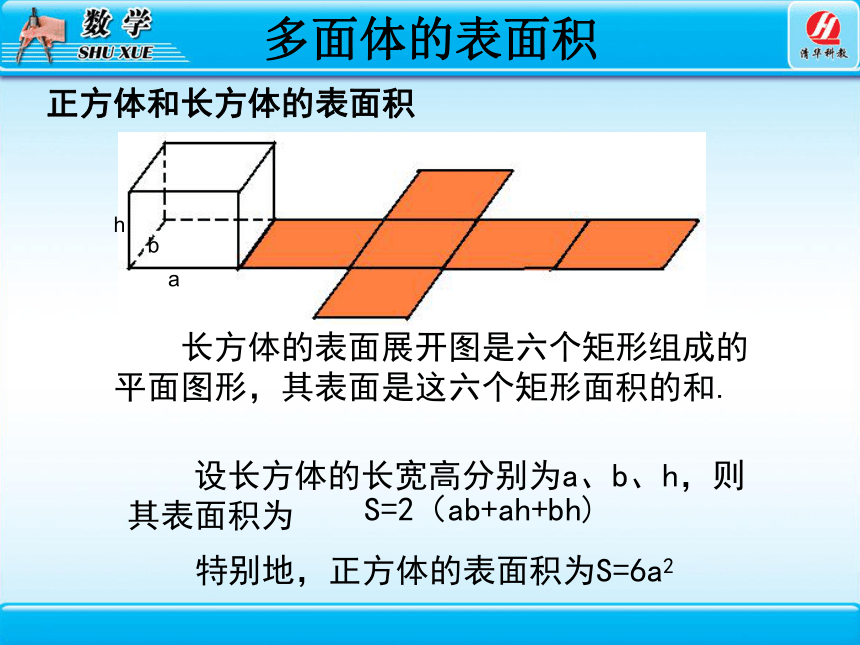
多面体的表面积
正方体和长方体的表面积
长方体的表面展开图是六个矩形组成的平面图形,其表面是这六个矩形面积的和.
S=2(ab+ah+bh)
a
b
h
特别地,正方体的表面积为S=6a2
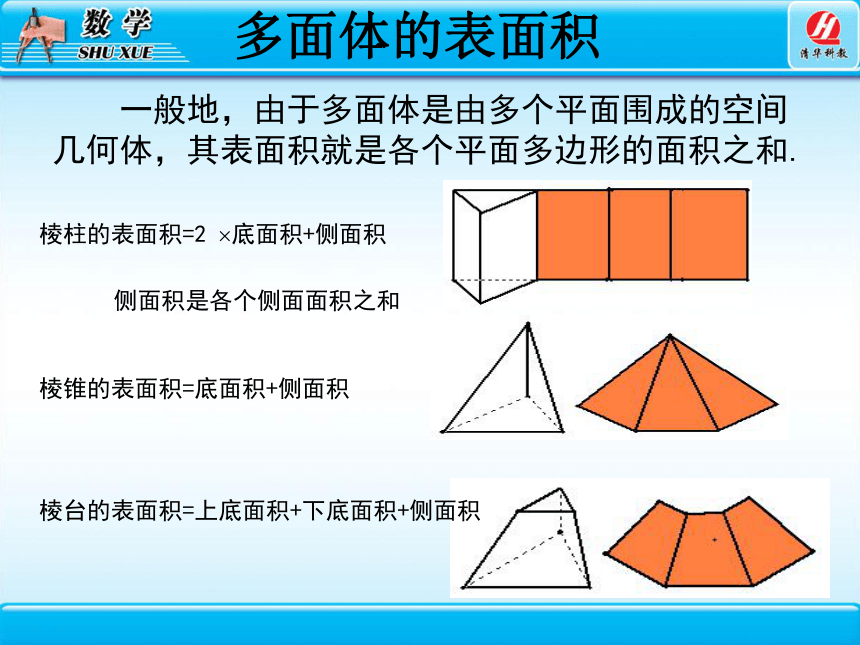
多面体的表面积
一般地,由于多面体是由多个平面围成的空间几何体,其表面积就是各个平面多边形的面积之和.
棱柱的表面积=2 底面积+侧面积
棱锥的表面积=底面积+侧面积
侧面积是各个侧面面积之和
棱台的表面积=上底面积+下底面积+侧面积
多面体的表面积
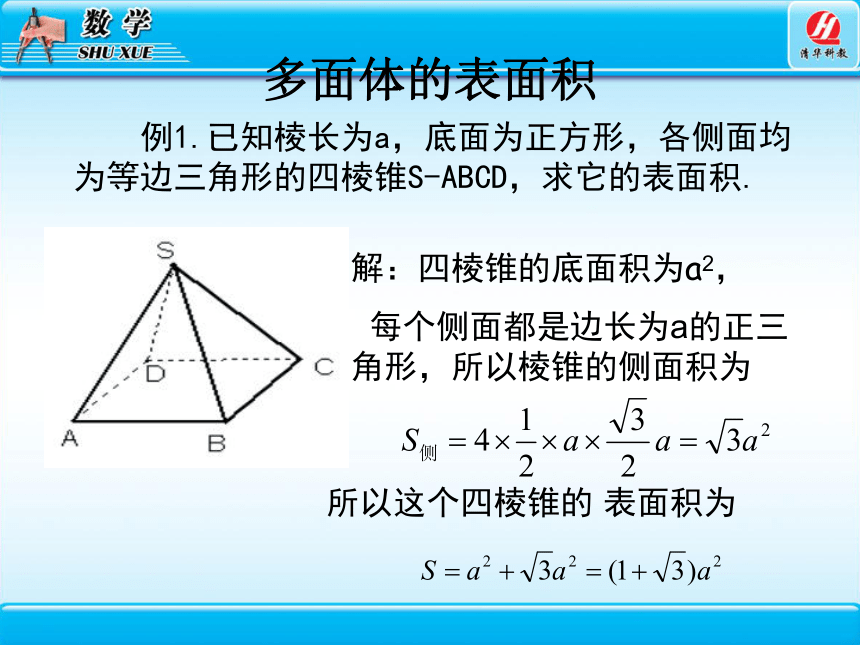
例1.已知棱长为a,底面为正方形,各侧面均为等边三角形的四棱锥S-ABCD,求它的表面积.
解:四棱锥的底面积为a2,
每个侧面都是边长为a的正三角形,所以棱锥的侧面积为
所以这个四棱锥的 表面积为
旋转体的表面积
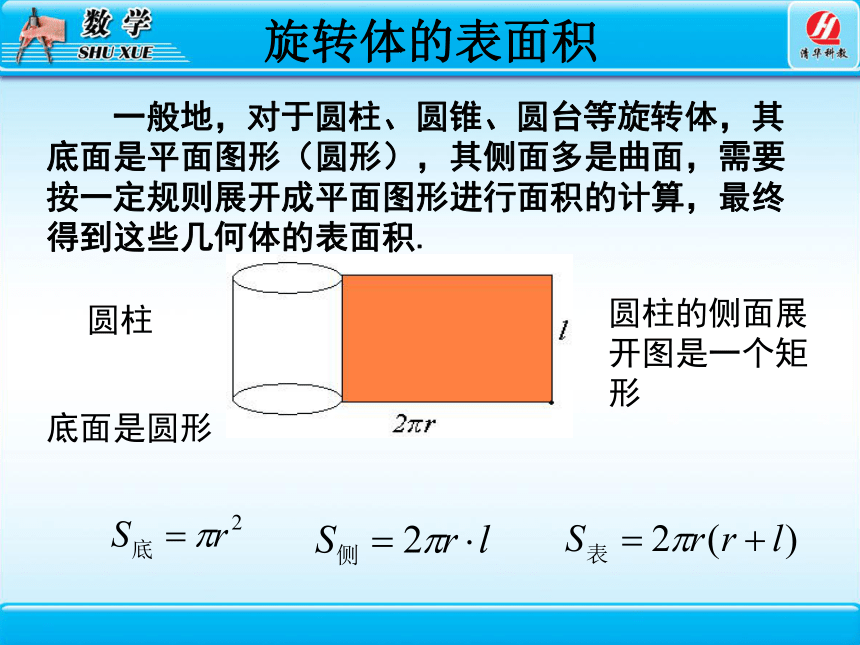
圆柱
一般地,对于圆柱、圆锥、圆台等旋转体,其底面是平面图形(圆形),其侧面多是曲面,需要按一定规则展开成平面图形进行面积的计算,最终得到这些几何体的表面积.
圆柱的侧面展开图是一个矩形
底面是圆形
旋转体的表面积
圆锥
侧面展开图是一个扇形
底面是圆形
圆台
底面是圆形
侧面展开图是一个扇状环形
旋转体的表面积
旋转体的表面积
例2.一个圆台形花盆盆口直径为20cm,盆底直径为15cm,底部渗水圆孔直径为1.5cm,盆壁长15cm,为了美化花盆的外观,需要涂油漆. 已知每平方米用100毫升油漆,涂100个这样的花盆需要多少油漆(精确到1毫升)?
20
20
15
解:由圆台的表面积公式得一个花盆外壁的表面积
所以涂100个花盆需油漆:0.1 100 100=1000(毫升).
空间几何体的体积
体积:几何体所占空间的大小
长方体的体积=长×宽×高
正方体的体积=棱长3
棱柱和圆柱的体积
高h
柱体的体积 V=Sh
高h
高h
底面积S
高h
棱锥和圆锥的体积
A
B
C
D
E
O
S
底面积S
高h
棱台和圆台的体积
高h
例3.有一堆规格相同的铁制六角螺帽共重5.8kg(铁的密度是7.8g/cm3),已知螺帽的底面是正六边形,边长为12mm,内孔直径为10mm,高为10mm,问这堆螺帽大约有多少个?
V≈2956(mm3)=2.956(cm3)
5.8×100÷7.8×2.956
≈252(个)
解答:
小结
常见平面图形的面积
多面体的表面积和体积
棱柱、棱锥、棱台的表面积和体积
旋转体的表面积和体积
圆柱、圆锥、圆台的表面积和体积
作业
P27 练习1,2
P28-29 习题1.3 A组 1,2,3,4,5,6
球的体积和表面积
1.3.2
球的表面积
球
球的体积
球面距离
球的体积和表面积
设球的半径为R,则有体积公式和表面积公式
R
解:设球的半径为R,则圆柱的底面半径为R,高为2R.
球的体积和表面积
例1 如图,圆柱的底面直径与高都等于球的直径,求证:(1)球的体积等于圆柱体积的 ;
(2)球的表面积等于圆柱的侧面积.
1)因为
2)因为
球的体积和表面积
例2. 已知正方体的八个顶点都在球O的球面上,且正方体的棱长为a,求球O的表面积和体积.
A
C′
o
解答:正方体的一条对角线是球的一条直径,所以球的半径为
球的体积和表面积
例3 已知A、B、C为球面上三点,AC=BC=6,AB=4,球心O与△ABC的外心M的距离等于球半径的一半,求这个球的表面积和体积.
A
B
C
O
M
A
B
C
O
M
球面距离
球面距离
即球面上两点间的最短距离,是指经过这两点和球心的大圆的劣弧的长度.
球心O
A
B
大圆圆弧
O
A
B
大圆劣弧的圆心角为α弧度,半径为R,则弧长为
L=αR
球面距离
例4. 已知地球的半径为R,在地球的赤道上经度差为1200的两点间距离.
o
A
B
答案:
作业
P28 练习1,2,3
P29-30 习题 B组 1,2,3
空间几何体的表面积与体积
1.3
主要内容
1.3.2 球的表面积和体积
1.3.1 柱体、椎体、台体的表面积与体积
1.3.1
柱体、锥体、台体的表面积与体积
什么是面积?
面积:平面图形所占平面的大小
S=ab
a
b
A
a
h
B
C
a
b
h
a
b
A
r
圆心角为n0
r
c
特殊平面图形的面积
正三角形的面积
正六边形的面积
正方形的面积
a
a
a
设长方体的长宽高分别为a、b、h,则其表面积为
多面体的表面积
正方体和长方体的表面积
长方体的表面展开图是六个矩形组成的平面图形,其表面是这六个矩形面积的和.
S=2(ab+ah+bh)
a
b
h
特别地,正方体的表面积为S=6a2
多面体的表面积
一般地,由于多面体是由多个平面围成的空间几何体,其表面积就是各个平面多边形的面积之和.
棱柱的表面积=2 底面积+侧面积
棱锥的表面积=底面积+侧面积
侧面积是各个侧面面积之和
棱台的表面积=上底面积+下底面积+侧面积
多面体的表面积
例1.已知棱长为a,底面为正方形,各侧面均为等边三角形的四棱锥S-ABCD,求它的表面积.
解:四棱锥的底面积为a2,
每个侧面都是边长为a的正三角形,所以棱锥的侧面积为
所以这个四棱锥的 表面积为
旋转体的表面积
圆柱
一般地,对于圆柱、圆锥、圆台等旋转体,其底面是平面图形(圆形),其侧面多是曲面,需要按一定规则展开成平面图形进行面积的计算,最终得到这些几何体的表面积.
圆柱的侧面展开图是一个矩形
底面是圆形
旋转体的表面积
圆锥
侧面展开图是一个扇形
底面是圆形
圆台
底面是圆形
侧面展开图是一个扇状环形
旋转体的表面积
旋转体的表面积
例2.一个圆台形花盆盆口直径为20cm,盆底直径为15cm,底部渗水圆孔直径为1.5cm,盆壁长15cm,为了美化花盆的外观,需要涂油漆. 已知每平方米用100毫升油漆,涂100个这样的花盆需要多少油漆(精确到1毫升)?
20
20
15
解:由圆台的表面积公式得一个花盆外壁的表面积
所以涂100个花盆需油漆:0.1 100 100=1000(毫升).
空间几何体的体积
体积:几何体所占空间的大小
长方体的体积=长×宽×高
正方体的体积=棱长3
棱柱和圆柱的体积
高h
柱体的体积 V=Sh
高h
高h
底面积S
高h
棱锥和圆锥的体积
A
B
C
D
E
O
S
底面积S
高h
棱台和圆台的体积
高h
例3.有一堆规格相同的铁制六角螺帽共重5.8kg(铁的密度是7.8g/cm3),已知螺帽的底面是正六边形,边长为12mm,内孔直径为10mm,高为10mm,问这堆螺帽大约有多少个?
V≈2956(mm3)=2.956(cm3)
5.8×100÷7.8×2.956
≈252(个)
解答:
小结
常见平面图形的面积
多面体的表面积和体积
棱柱、棱锥、棱台的表面积和体积
旋转体的表面积和体积
圆柱、圆锥、圆台的表面积和体积
作业
P27 练习1,2
P28-29 习题1.3 A组 1,2,3,4,5,6
球的体积和表面积
1.3.2
球的表面积
球
球的体积
球面距离
球的体积和表面积
设球的半径为R,则有体积公式和表面积公式
R
解:设球的半径为R,则圆柱的底面半径为R,高为2R.
球的体积和表面积
例1 如图,圆柱的底面直径与高都等于球的直径,求证:(1)球的体积等于圆柱体积的 ;
(2)球的表面积等于圆柱的侧面积.
1)因为
2)因为
球的体积和表面积
例2. 已知正方体的八个顶点都在球O的球面上,且正方体的棱长为a,求球O的表面积和体积.
A
C′
o
解答:正方体的一条对角线是球的一条直径,所以球的半径为
球的体积和表面积
例3 已知A、B、C为球面上三点,AC=BC=6,AB=4,球心O与△ABC的外心M的距离等于球半径的一半,求这个球的表面积和体积.
A
B
C
O
M
A
B
C
O
M
球面距离
球面距离
即球面上两点间的最短距离,是指经过这两点和球心的大圆的劣弧的长度.
球心O
A
B
大圆圆弧
O
A
B
大圆劣弧的圆心角为α弧度,半径为R,则弧长为
L=αR
球面距离
例4. 已知地球的半径为R,在地球的赤道上经度差为1200的两点间距离.
o
A
B
答案:
作业
P28 练习1,2,3
P29-30 习题 B组 1,2,3
