4.1圆的方程
图片预览










文档简介
(共33张PPT)
4.1
圆的方程
主要内容
4.1.2 圆的一般方程
4.1.1 圆的标准方程
4.1.1
圆的标准方程
在平面直角坐标系中,如何确定一个圆呢?
在平面直角坐标系中,两点确定一条直线,一点和倾斜角也能确定一条直线.
平面内到定点的距离等于定长的点的集合.
定点
定长
圆心
半径
·
r
C
当圆心位置与半径大小确定后,圆就唯一确定了.因此一个圆最基本要素是圆心和半径.
如图,在直角坐标系中,圆心(点)A的位置用坐标(a,b)表示,半径 r 的大小等于圆上任意点M(x, y)与圆心A (a,b)的距离.
x
O
C
M(x,y)
y
x
y
O
C
M(x,y)
圆心C(a,b),半径r
特别地,若圆心为O(0,0),则圆的方程为:
标准方程
圆的标准方程
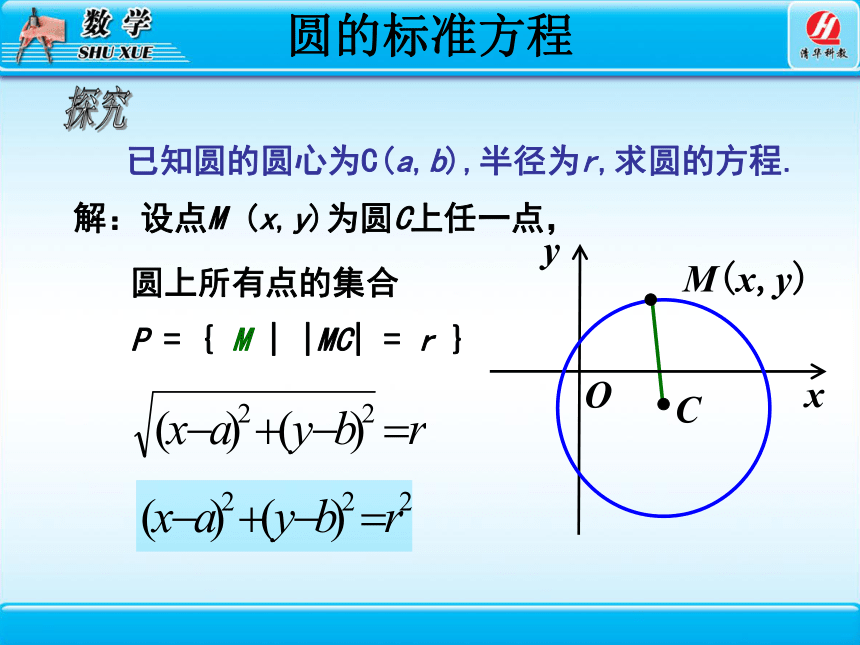
已知圆的圆心为C(a,b),半径为r,求圆的方程.
x
y
O
C
M(x,y)
解:设点M (x,y)为圆C上任一点,
P = { M | |MC| = r }
圆上所有点的集合
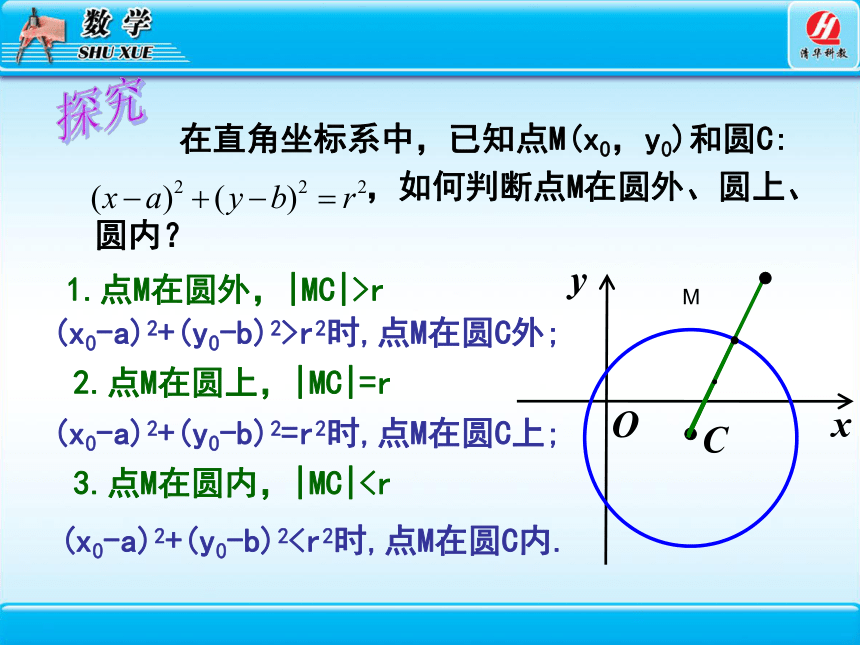
在直角坐标系中,已知点M(x0,y0)和圆C:
,如何判断点M在圆外、圆上、圆内?
(x0-a)2+(y0-b)2>r2时,点M在圆C外;
(x0-a)2+(y0-b)2=r2时,点M在圆C上;
(x0-a)2+(y0-b)2x
y
O
C
M
1.点M在圆外,|MC|>r
2.点M在圆上,|MC|=r
3.点M在圆内,|MC|例1 写出圆心为 ,半径长等于5的圆的方程,并判断点 , 是否在这个圆上.
解:
圆心是 ,半径长等于5的圆的标准方程是
把 的坐标代入圆的方程,左右两边相等,点 的坐标适合圆的方程,所以点 在这个圆上;
把点 的坐标代入方程,左右两边不相等, 点 的坐标不适合圆的方程,所以点 不在这个 圆上.
例2 的三个顶点的坐标分别为A(5,1), B(7,-3),C(2, -8) ,求它的外接圆的方程.
分析:不在同一条直线上的三个点可以确定一个圆,三角形有唯一的外接圆.
解:设所求圆的方程是
因为A(5,1), B(7,-3),C(2, -8) 都在圆上,所以它们的坐标都满足圆的方程,于是
所以, 的外接圆的方程是
解此方程组,得
结论:在平面直角坐标系中,已知三个点的坐标可以确定一个圆的方程
例3 已知圆心为C 的圆经过点A(1,1)和B(2,-2),且圆心C 在直线上l:x - y+1=0,求圆心为C 的圆的标准方程.
分析:如图,确定一个圆只需确定圆心位置与半径大小.圆心为C 的圆经过点A(1,1)和B(2,-2),由于圆心C 与A,B 两点的距离相等,所以圆心C 在线段AB 的垂直平分线 上.又圆心C 在直线l 上,因此圆心C 是直线 l 与直线 的交点,半径长等于|CA|或|CB|.
解:因为A(1, 1)和B(2, -2),所以线段AB的中点D的坐标
,直线AB的斜率
B
x
o
y
A
C
l
即
因此线段AB 的垂直平分线 的方程是
圆心C 的坐标是方程组
的解.
解此方程组,得
所以圆心C 的坐标是
圆心为C 的圆的半径长
所以,圆心为C 的圆的标准方程是
小结
1.圆的标准方程的结构特点.
2.点与圆的位置关系的判定.
3.求圆的标准方程的方法:
①待定系数法;②代入法.
作业
P120-121练习:1,2,3,4
4.1.2
圆的一般方程
1. 圆的标准方程 展开可得到一个什么式子
2. 方程
与 都表示的图形是圆吗?
解:分别配方得
第一个方程表示以(1,-2)为圆心,2为半径长的圆. 第二个方程没有实数解,不存在点的坐标(x,y)满足这个方程,它不表示任何图形.
方程 在什么条件下表示圆?
(1)当 时,
表示圆,
(2)当 时,
表示点
(3)当 时,
不表示任何图形
圆的一般方程
其中
练习
判断下列方程是不是表示圆
表示以(2,3)为圆心,以3为半径的圆
表示点(2,3)
不表示任何图形
比较
圆的一般方程和圆的标准方程各有什么特点?
圆的一般方程的特点 :
(1)x2、y2 的系数相同,都不为0.
(2)没有形如xy的二次项.
圆的一般方程与圆的标准方程各有特点:
(1)圆的标准方程带有明显的几何的影子,圆心和半径一目了然.
(2)圆的一般方程表现出明显的代数的形式与结构,更适合方程理论的运用.
例1 求过三点O(0,0),A(1,1),B(4,2)的圆的方程,并求出这个圆的半径长和圆心坐标.
解:设所求圆的方程为:
因为A(5,1),B (7,-3),C(2,8)都在圆上
所求圆的方程为
上述解法用了一般方程,请你比较上节课的标准方程的解法.
用标准方程解答
待定系数法
解:设所求圆的方程为:
因为A(5,1),B (7,-3),C(2,8)都在圆上
所求圆的方程为
例2 已知线段AB的端点B的坐标是(4,3),端点A在圆(x+1)2+y2=4 上运动,求线段AB的中点M的轨迹方程.
y
A
B
M
x
o
例2 方程
表示的图形是一个圆,求a 的取值范围.
小结
1.圆的一般方程的结构特点.
2.用配方法化一般方程为标准方程.
3.求圆的一般方程的方法:
①待定系数法;②代入法.
小结:求圆的方程
几何方法
求圆心坐标 (两条直线的交点)(常用弦的中垂线)
求半径 (圆心到圆上一点的距离)
写出圆的标准方程
待定系数法
列关于a,b,r(或D,E,F)的方程组
解出a,b,r(或D,E,F),写出标准方程(或一般方程)
作业
P123练习:1,2,3.
P124习题4.1A组:1,2,3,4
4.1
圆的方程
主要内容
4.1.2 圆的一般方程
4.1.1 圆的标准方程
4.1.1
圆的标准方程
在平面直角坐标系中,如何确定一个圆呢?
在平面直角坐标系中,两点确定一条直线,一点和倾斜角也能确定一条直线.
平面内到定点的距离等于定长的点的集合.
定点
定长
圆心
半径
·
r
C
当圆心位置与半径大小确定后,圆就唯一确定了.因此一个圆最基本要素是圆心和半径.
如图,在直角坐标系中,圆心(点)A的位置用坐标(a,b)表示,半径 r 的大小等于圆上任意点M(x, y)与圆心A (a,b)的距离.
x
O
C
M(x,y)
y
x
y
O
C
M(x,y)
圆心C(a,b),半径r
特别地,若圆心为O(0,0),则圆的方程为:
标准方程
圆的标准方程
已知圆的圆心为C(a,b),半径为r,求圆的方程.
x
y
O
C
M(x,y)
解:设点M (x,y)为圆C上任一点,
P = { M | |MC| = r }
圆上所有点的集合
在直角坐标系中,已知点M(x0,y0)和圆C:
,如何判断点M在圆外、圆上、圆内?
(x0-a)2+(y0-b)2>r2时,点M在圆C外;
(x0-a)2+(y0-b)2=r2时,点M在圆C上;
(x0-a)2+(y0-b)2
y
O
C
M
1.点M在圆外,|MC|>r
2.点M在圆上,|MC|=r
3.点M在圆内,|MC|
解:
圆心是 ,半径长等于5的圆的标准方程是
把 的坐标代入圆的方程,左右两边相等,点 的坐标适合圆的方程,所以点 在这个圆上;
把点 的坐标代入方程,左右两边不相等, 点 的坐标不适合圆的方程,所以点 不在这个 圆上.
例2 的三个顶点的坐标分别为A(5,1), B(7,-3),C(2, -8) ,求它的外接圆的方程.
分析:不在同一条直线上的三个点可以确定一个圆,三角形有唯一的外接圆.
解:设所求圆的方程是
因为A(5,1), B(7,-3),C(2, -8) 都在圆上,所以它们的坐标都满足圆的方程,于是
所以, 的外接圆的方程是
解此方程组,得
结论:在平面直角坐标系中,已知三个点的坐标可以确定一个圆的方程
例3 已知圆心为C 的圆经过点A(1,1)和B(2,-2),且圆心C 在直线上l:x - y+1=0,求圆心为C 的圆的标准方程.
分析:如图,确定一个圆只需确定圆心位置与半径大小.圆心为C 的圆经过点A(1,1)和B(2,-2),由于圆心C 与A,B 两点的距离相等,所以圆心C 在线段AB 的垂直平分线 上.又圆心C 在直线l 上,因此圆心C 是直线 l 与直线 的交点,半径长等于|CA|或|CB|.
解:因为A(1, 1)和B(2, -2),所以线段AB的中点D的坐标
,直线AB的斜率
B
x
o
y
A
C
l
即
因此线段AB 的垂直平分线 的方程是
圆心C 的坐标是方程组
的解.
解此方程组,得
所以圆心C 的坐标是
圆心为C 的圆的半径长
所以,圆心为C 的圆的标准方程是
小结
1.圆的标准方程的结构特点.
2.点与圆的位置关系的判定.
3.求圆的标准方程的方法:
①待定系数法;②代入法.
作业
P120-121练习:1,2,3,4
4.1.2
圆的一般方程
1. 圆的标准方程 展开可得到一个什么式子
2. 方程
与 都表示的图形是圆吗?
解:分别配方得
第一个方程表示以(1,-2)为圆心,2为半径长的圆. 第二个方程没有实数解,不存在点的坐标(x,y)满足这个方程,它不表示任何图形.
方程 在什么条件下表示圆?
(1)当 时,
表示圆,
(2)当 时,
表示点
(3)当 时,
不表示任何图形
圆的一般方程
其中
练习
判断下列方程是不是表示圆
表示以(2,3)为圆心,以3为半径的圆
表示点(2,3)
不表示任何图形
比较
圆的一般方程和圆的标准方程各有什么特点?
圆的一般方程的特点 :
(1)x2、y2 的系数相同,都不为0.
(2)没有形如xy的二次项.
圆的一般方程与圆的标准方程各有特点:
(1)圆的标准方程带有明显的几何的影子,圆心和半径一目了然.
(2)圆的一般方程表现出明显的代数的形式与结构,更适合方程理论的运用.
例1 求过三点O(0,0),A(1,1),B(4,2)的圆的方程,并求出这个圆的半径长和圆心坐标.
解:设所求圆的方程为:
因为A(5,1),B (7,-3),C(2,8)都在圆上
所求圆的方程为
上述解法用了一般方程,请你比较上节课的标准方程的解法.
用标准方程解答
待定系数法
解:设所求圆的方程为:
因为A(5,1),B (7,-3),C(2,8)都在圆上
所求圆的方程为
例2 已知线段AB的端点B的坐标是(4,3),端点A在圆(x+1)2+y2=4 上运动,求线段AB的中点M的轨迹方程.
y
A
B
M
x
o
例2 方程
表示的图形是一个圆,求a 的取值范围.
小结
1.圆的一般方程的结构特点.
2.用配方法化一般方程为标准方程.
3.求圆的一般方程的方法:
①待定系数法;②代入法.
小结:求圆的方程
几何方法
求圆心坐标 (两条直线的交点)(常用弦的中垂线)
求半径 (圆心到圆上一点的距离)
写出圆的标准方程
待定系数法
列关于a,b,r(或D,E,F)的方程组
解出a,b,r(或D,E,F),写出标准方程(或一般方程)
作业
P123练习:1,2,3.
P124习题4.1A组:1,2,3,4
