4.3空间直角坐标系
图片预览




文档简介
(共27张PPT)
4.3
空间直角坐标系
主要内容
4.3.2 空间两点间的距离公式
4.3.1 空间直角坐标系
4.3.1
空间直角坐标系
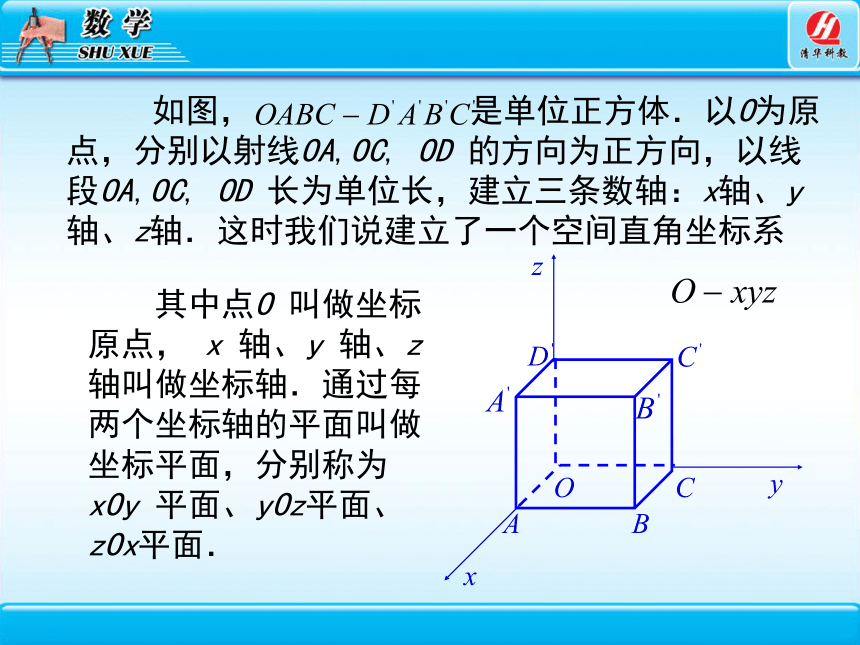
如图, 是单位正方体.以O为原点,分别以射线OA,OC, OD 的方向为正方向,以线段OA,OC, OD 长为单位长,建立三条数轴:x轴、y轴、z轴.这时我们说建立了一个空间直角坐标系
A
B
C
O
y
x
z
其中点O 叫做坐标原点, x 轴、y 轴、z轴叫做坐标轴.通过每两个坐标轴的平面叫做坐标平面,分别称为xOy 平面、yOz平面、zOx平面.
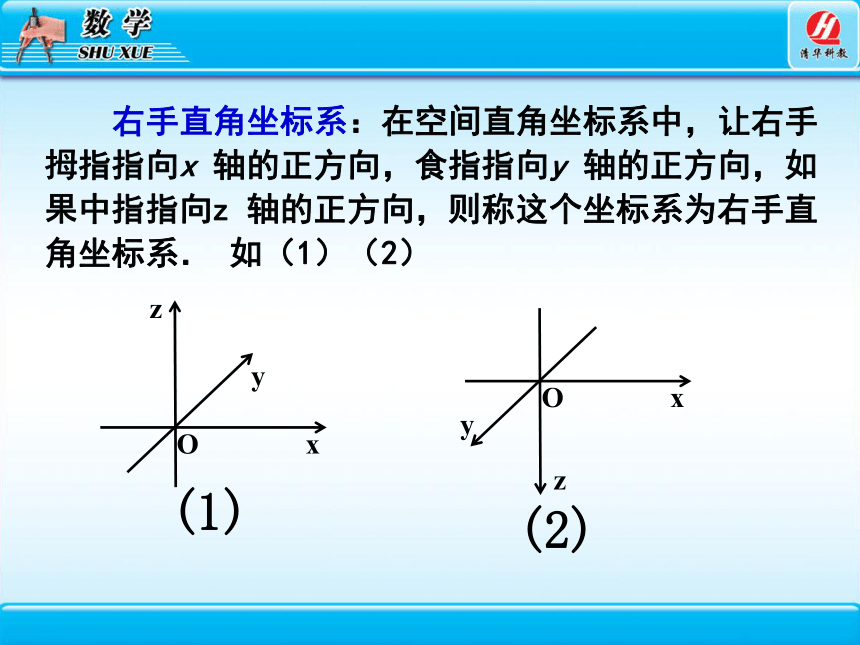
右手直角坐标系:在空间直角坐标系中,让右手拇指指向x 轴的正方向,食指指向y 轴的正方向,如果中指指向z 轴的正方向,则称这个坐标系为右手直角坐标系. 如(1)(2)
x
y
z
O
x
y
z
O
(1)
(2)
x
y
z
O
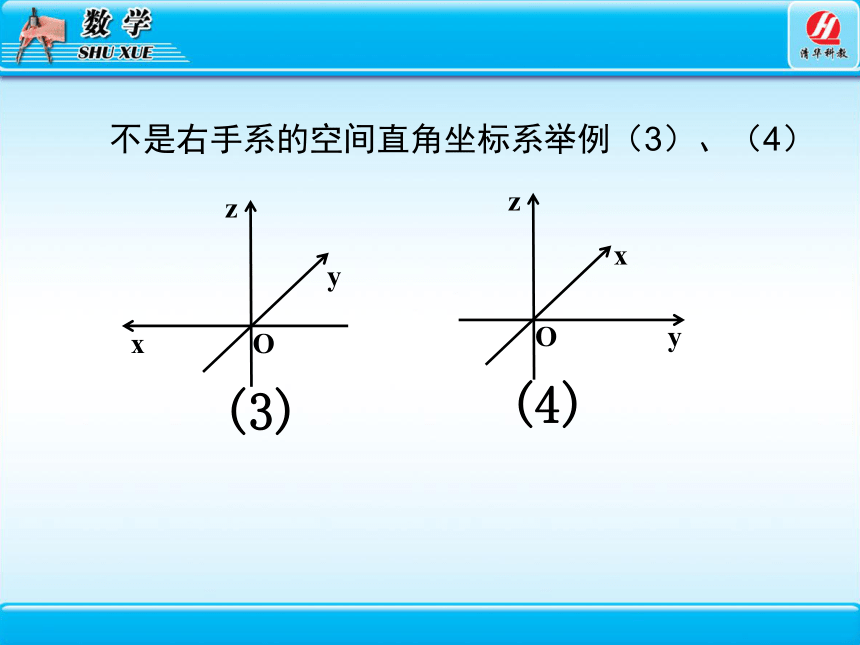
(3)
x
y
z
O
(4)
不是右手系的空间直角坐标系举例(3)、(4)
x
y
z
O
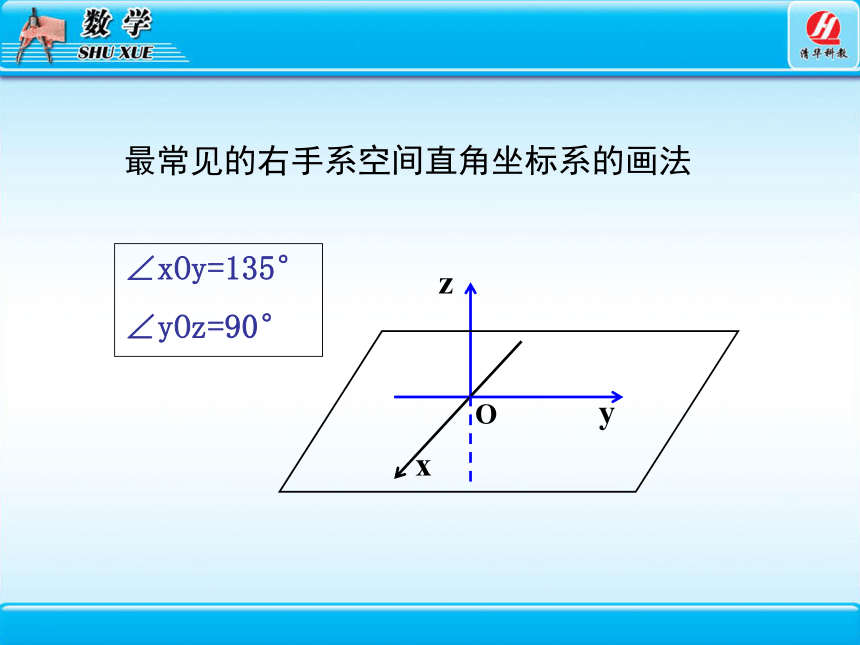
最常见的右手系空间直角坐标系的画法
∠xOy=135°∠yOz=90°
空间三维坐标
空间一点M的坐标可以用有序实数组(x,y,z)来表示. 记点M(x,y,z)
x叫做点M的横坐标
y叫做点M的纵坐标
z叫做点M的竖坐标
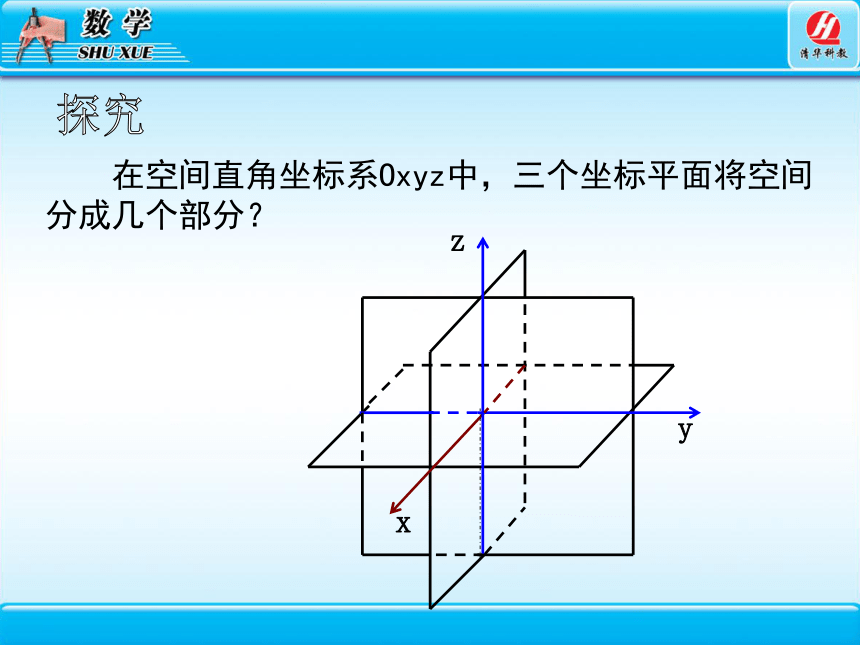
在空间直角坐标系Oxyz中,三个坐标平面将空间分成几个部分?
x
z
y
x轴、y轴、z轴上的点的坐标有何特点?xOy平面、yOz平面、xOz平面上的点的坐标有何特点?
x
z
y
x
y
z
O
O
y
x
z
A
C
B
例1 如图,在长方体OABC-D′A′B′C′中,|OA|=3, |OC|=4,|OD′|=2,写出长方体各顶点的坐标.
解答:O(0,0,0)
A(3,0,0)
C(0,4,0)
D’(0,0,2)
A’(3,0,2)
B’(3,4,2)
C’(0,4,2)
B(3,4,0)
例2 结晶体的基本单位称为晶胞,下图是食盐晶胞的示意图(可看成是八个棱长为0.5的小正方体堆积成的正方体),其中色点代表钠原子,黑点代表氯原子.如图建立直角坐标系Oxyz,试写出全部钠原子所在位置的坐标.
x
y
z
O
解:把图中的钠原子分成上、中、下三层来写它们所在位置的坐标.
中层的原子所在的平面平行于平面,与轴交点的
竖坐标为,所以,这四个钠原子所在位置的坐标分别
是( ,0, ),(1, , ),( ,1, ),
(0, , );
下层的原子全部在平面上,它们所在位置的竖坐标全是0,所以这五个钠原子所在位置的坐标分别是(0,0,0),(1,0,0),(1,1,0),(0,1,0)( , ,0);
上层的原子所在的平面平行于平面,与轴交点的竖坐标为1,所以,这五个钠原子所在位置的坐标分别是(0,0,1),(1,0,1),(1,1,1),
(0,1,1),( , ,1).
空间直角坐标系的建立
空间直角坐标
小结
作业
P136练习:1,2,3.
P138习题4.3 A 组:1,2.
4.3.2
空间两点间的距离公式
类比平面直角坐标系中两点间距离公式及其推导,你能猜想一下空间两点P1(x1,y1,z1), P2(x2,y2,z2)间的距离公式吗?
x
y
P1(x1,y1)
P2(x2, y2)
Q(x2,y1)
O
x2
y2
x1
y1
x
y
P1(x1,y1)
P2(x2,y2)
O
已知平面上两点P1(x1,y1)和P2(x2,y2),则点P1和P2的距离|P1P2|为
空间两点P1(x1,y1,z1),P2(x2,y2,z2)间的距离公式
1.在空间直角坐标系中,坐标平面上的点
A(x,y,0),B(0,y,z),C(x,0,z), 与坐标原点O的距离分别是什么?
x
y
z
O
A
B
C
例1 在空间中,已知点A(1,0,-1),B(4,3,-1),求A、B两点之间的距离.
例2 已知两点 A(-4,1,7)和B(3,5,-2),点P在z轴上,若|PA|=|PB|,求点P的坐标.
例3 如图,点P、Q分别在棱长为1的正方体的对角线AB和棱CD上运动,求P、Q两点间的距离的最小值,并指出此时P、Q两点的位置.
O
x
y
z
B
A
C
P
Q
D
M
空间中两点间距离的坐标计算
类比思想:维度的升高,距离公式如何改变?
小结
作业
P132练习:1,2,3,4.
P133习题4.2B组:1,2,3.
4.3
空间直角坐标系
主要内容
4.3.2 空间两点间的距离公式
4.3.1 空间直角坐标系
4.3.1
空间直角坐标系
如图, 是单位正方体.以O为原点,分别以射线OA,OC, OD 的方向为正方向,以线段OA,OC, OD 长为单位长,建立三条数轴:x轴、y轴、z轴.这时我们说建立了一个空间直角坐标系
A
B
C
O
y
x
z
其中点O 叫做坐标原点, x 轴、y 轴、z轴叫做坐标轴.通过每两个坐标轴的平面叫做坐标平面,分别称为xOy 平面、yOz平面、zOx平面.
右手直角坐标系:在空间直角坐标系中,让右手拇指指向x 轴的正方向,食指指向y 轴的正方向,如果中指指向z 轴的正方向,则称这个坐标系为右手直角坐标系. 如(1)(2)
x
y
z
O
x
y
z
O
(1)
(2)
x
y
z
O
(3)
x
y
z
O
(4)
不是右手系的空间直角坐标系举例(3)、(4)
x
y
z
O
最常见的右手系空间直角坐标系的画法
∠xOy=135°∠yOz=90°
空间三维坐标
空间一点M的坐标可以用有序实数组(x,y,z)来表示. 记点M(x,y,z)
x叫做点M的横坐标
y叫做点M的纵坐标
z叫做点M的竖坐标
在空间直角坐标系Oxyz中,三个坐标平面将空间分成几个部分?
x
z
y
x轴、y轴、z轴上的点的坐标有何特点?xOy平面、yOz平面、xOz平面上的点的坐标有何特点?
x
z
y
x
y
z
O
O
y
x
z
A
C
B
例1 如图,在长方体OABC-D′A′B′C′中,|OA|=3, |OC|=4,|OD′|=2,写出长方体各顶点的坐标.
解答:O(0,0,0)
A(3,0,0)
C(0,4,0)
D’(0,0,2)
A’(3,0,2)
B’(3,4,2)
C’(0,4,2)
B(3,4,0)
例2 结晶体的基本单位称为晶胞,下图是食盐晶胞的示意图(可看成是八个棱长为0.5的小正方体堆积成的正方体),其中色点代表钠原子,黑点代表氯原子.如图建立直角坐标系Oxyz,试写出全部钠原子所在位置的坐标.
x
y
z
O
解:把图中的钠原子分成上、中、下三层来写它们所在位置的坐标.
中层的原子所在的平面平行于平面,与轴交点的
竖坐标为,所以,这四个钠原子所在位置的坐标分别
是( ,0, ),(1, , ),( ,1, ),
(0, , );
下层的原子全部在平面上,它们所在位置的竖坐标全是0,所以这五个钠原子所在位置的坐标分别是(0,0,0),(1,0,0),(1,1,0),(0,1,0)( , ,0);
上层的原子所在的平面平行于平面,与轴交点的竖坐标为1,所以,这五个钠原子所在位置的坐标分别是(0,0,1),(1,0,1),(1,1,1),
(0,1,1),( , ,1).
空间直角坐标系的建立
空间直角坐标
小结
作业
P136练习:1,2,3.
P138习题4.3 A 组:1,2.
4.3.2
空间两点间的距离公式
类比平面直角坐标系中两点间距离公式及其推导,你能猜想一下空间两点P1(x1,y1,z1), P2(x2,y2,z2)间的距离公式吗?
x
y
P1(x1,y1)
P2(x2, y2)
Q(x2,y1)
O
x2
y2
x1
y1
x
y
P1(x1,y1)
P2(x2,y2)
O
已知平面上两点P1(x1,y1)和P2(x2,y2),则点P1和P2的距离|P1P2|为
空间两点P1(x1,y1,z1),P2(x2,y2,z2)间的距离公式
1.在空间直角坐标系中,坐标平面上的点
A(x,y,0),B(0,y,z),C(x,0,z), 与坐标原点O的距离分别是什么?
x
y
z
O
A
B
C
例1 在空间中,已知点A(1,0,-1),B(4,3,-1),求A、B两点之间的距离.
例2 已知两点 A(-4,1,7)和B(3,5,-2),点P在z轴上,若|PA|=|PB|,求点P的坐标.
例3 如图,点P、Q分别在棱长为1的正方体的对角线AB和棱CD上运动,求P、Q两点间的距离的最小值,并指出此时P、Q两点的位置.
O
x
y
z
B
A
C
P
Q
D
M
空间中两点间距离的坐标计算
类比思想:维度的升高,距离公式如何改变?
小结
作业
P132练习:1,2,3,4.
P133习题4.2B组:1,2,3.
