导数及其应用测试题(Word含有详细答案)
文档属性
| 名称 | 导数及其应用测试题(Word含有详细答案) |
|
|
| 格式 | doc | ||
| 文件大小 | 529.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-01 00:00:00 | ||
图片预览




文档简介
兴国三中高二数学(文)期末复习题《导数及其应用》
命题:高二数学备课组
一、选择题
1.是函数在点处取极值的:
A.充分不必要条件
B.必要不充分条件
C.充要条件
D.既不充分又不必要条件
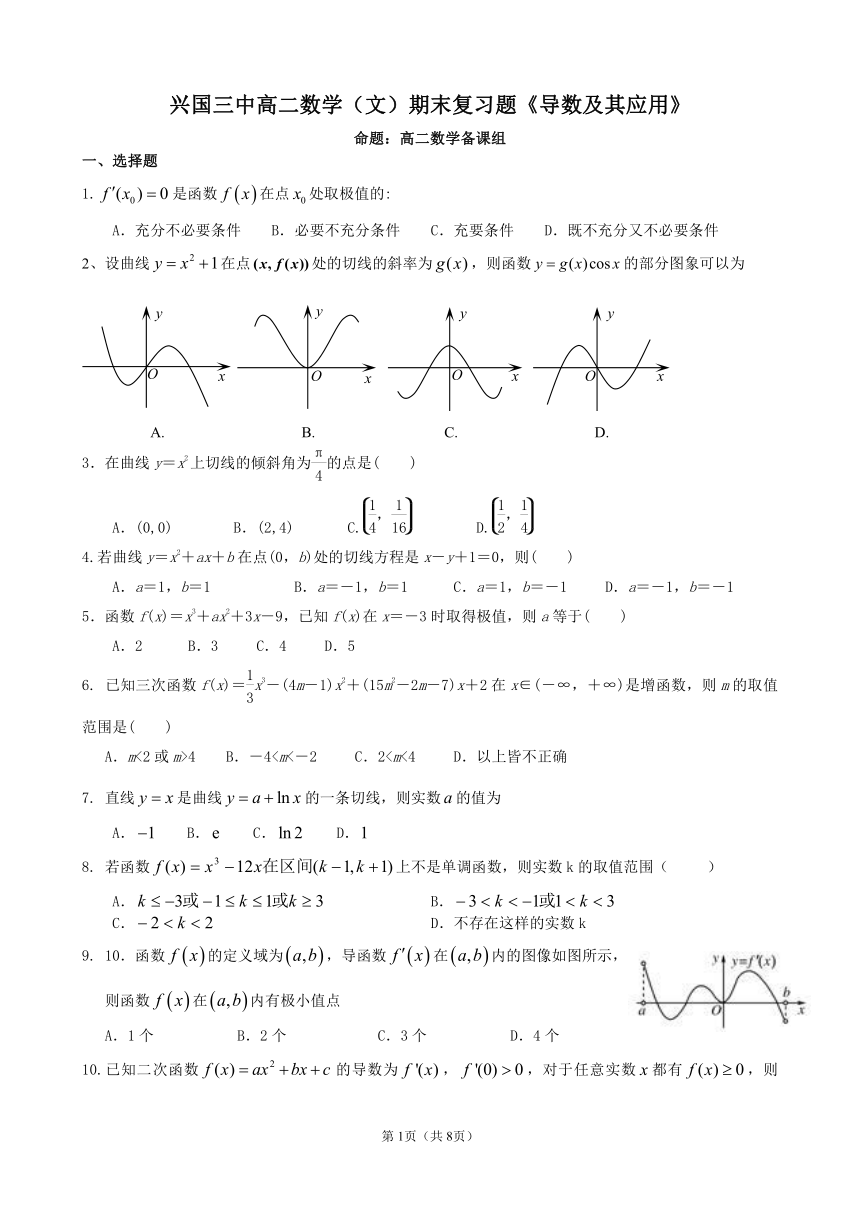
2、设曲线在点处的切线的斜率为,则函数的部分图象可以为
A.
B.
C.
D.
3.在曲线y=x2上切线的倾斜角为的点是( )
A.(0,0)
B.(2,4)
C.
D.
4.若曲线y=x2+ax+b在点(0,b)处的切线方程是x-y+1=0,则( )
A.a=1,b=1
B.a=-1,b=1
C.a=1,b=-1
D.a=-1,b=-1
5.函数f(x)=x3+ax2+3x-9,已知f(x)在x=-3时取得极值,则a等于( )
A.2
B.3
C.4
D.5
6.
已知三次函数f(x)=x3-(4m-1)x2+(15m2-2m-7)x+2在x∈(-∞,+∞)是增函数,则m的取值范围是( )
A.m<2或m>4
B.-4C.2D.以上皆不正确
7.
直线是曲线的一条切线,则实数的值为
A.
B.
C.
D.
8.
若函数上不是单调函数,则实数k的取值范围(
)
A.
B.
C.
D.不存在这样的实数k
9.
10.函数的定义域为,导函数在内的图像如图所示,
则函数在内有极小值点
A.1个
B.2个
C.3个
D.4个
10.已知二次函数的导数为,,对于任意实数都有,则的最小值为
A.
B.
C.
D.
二、填空题(本大题共4个小题,每小题5分,共20分)
11.函数的导数为_________________
12、已知函数在x=1处有极值为10,则f(2)等于____________.
13.函数在区间上的最大值是
14.已知函数在R上有两个极值点,则实数的取值范围是
15.
已知函数是定义在R上的奇函数,,,则不等式
的解集是
三、解答题(本大题共6小题,共80分,解答应写出文字说明,证明过程或演算步骤)
16.
设函数f(x)=sinx-cosx+x+1,017.
已知函数.
(Ⅰ)求的值;(Ⅱ)求函数的单调区间.
18.
设函数.
(1)求的单调区间和极值;
(2)若关于的方程有3个不同实根,求实数的取值范围.
(3)已知当恒成立,求实数的取值范围.
19.
已知是函数的一个极值点,其中
(1)求与的关系式;
(2)求的单调区间;
(3)当,函数的图象上任意一点的切线斜率恒大于,求的取值范围。
20.
已知函数
(I)当时,若函数在其定义域内是增函数,求b的取值范围;
(II)若的图象与x轴交于两点,且AB的中点为,求证:
21.
已知函数为自然对数的底数)
(1)求的单调区间,若有最值,请求出最值;
(2)是否存在正常数,使的图象有且只有一个公共点,且在该公共点处有共同的切线?若存在,求出的值,以及公共点坐标和公切线方程;若不存在,请说明理由。
兴国三中高二数学(文)期末复习《导数及其应用》参考答案
一、选择题:
题号
1
2
3
4
5
6
7
8
9
10
答案
B
A
D
A
D
D
D
B
A
C
二、填空题:
11.
;12.
18
13.;
14.;
15.
三、解答题
16.
[解析] f′(x)=cosx+sinx+1=sin(x+)+1 (0令f′(x)=0,即sin(x+)=-,
解之得x=π或x=π.
x,f′(x)以及f(x)变化情况如下表:
x
(0,π)
π
(π,π)
π
(π,2π)
f′(x)
+
0
-
0
+
f(x)
递增
π+2
递减
递增
∴f(x)的单调增区间为(0,π)和(π,2π)单调减区间为(π,π).
f极大(x)=f(π)=π+2,f极小(x)=f(π)=.
17.
解:(Ⅰ),所以.
(Ⅱ),
解,得或.
解,得.
所以,为函数的单调增区间,为函数的单调减区间.
18.
解:(1)
…………………1分
∴当,…………………2分
∴的单调递增区间是,单调递减区间是……3分
当;当.…………4分
(2)由(1)可知图象的大致形状及走向(图略)
∴当的图象有3个不同交点,……6分
即当时方程有三解.
…………………………………7分
(3)
∵上恒成立.
…………………………………………9分
令,由二次函数的性质,上是增函数,
∴∴所求的取值范围是……………………………………12分
19.
解:(1)因为是函数的一个极值点.所以
即所以
(2)由(1)知,
当时,有,当为化时,与的变化如下表:
1
-
0
+
0
-
单调递减
极小值
单调递增
极大值
单调递减
故由上表知,当时,在单调递减,在单调递增,在上单调
递减.
(3)由已知得,即又,所以,即
设,其函数图象开口向上,由题意知①式恒成立,所以
解之得所以即的取值范围为
20.(1)由题意:,在上递增,对恒成立,即对恒成立,只需,
,,当且仅当时取“=”,,的取值范围为
(2)由已知得,,两式相减,得:
,
由及,得:
,令,
且,,在上为减函数,
,又,
21.
解:(1)
①当恒成立
上是增函数,F只有一个单调递增区间(0,-∞),没有最值……3分
②当时,,
若,则上单调递减;
若,则上单调递增,
时,有极小值,也是最小值,
即…………6分
所以当时,的单调递减区间为
单调递增区间为,最小值为,无最大值…………7分
(2)方法一,若与的图象有且只有一个公共点,
则方程有且只有一解,所以函数有且只有一个零点…………8分[]
由(1)的结论可知…………10分
此时,
的图象的唯一公共点坐标为
又的图象在点处有共同的切线,
其方程为,即…………13分
综上所述,存在,使的图象有且只有一个公共点,且在该点处的公切线方程为…………14分
方法二:设图象的公共点坐标为,
根据题意得即
由②得,代入①得
从而…………10分
此时由(1)可知
时,
因此除外,再没有其它,使…………13分
故存在,使的图象有且只有一个公共点,且在该公共点处有共同的切线,易求得公共点坐标为,公切线方程为…………14分
第8页(共8页)
命题:高二数学备课组
一、选择题
1.是函数在点处取极值的:
A.充分不必要条件
B.必要不充分条件
C.充要条件
D.既不充分又不必要条件
2、设曲线在点处的切线的斜率为,则函数的部分图象可以为
A.
B.
C.
D.
3.在曲线y=x2上切线的倾斜角为的点是( )
A.(0,0)
B.(2,4)
C.
D.
4.若曲线y=x2+ax+b在点(0,b)处的切线方程是x-y+1=0,则( )
A.a=1,b=1
B.a=-1,b=1
C.a=1,b=-1
D.a=-1,b=-1
5.函数f(x)=x3+ax2+3x-9,已知f(x)在x=-3时取得极值,则a等于( )
A.2
B.3
C.4
D.5
6.
已知三次函数f(x)=x3-(4m-1)x2+(15m2-2m-7)x+2在x∈(-∞,+∞)是增函数,则m的取值范围是( )
A.m<2或m>4
B.-4
7.
直线是曲线的一条切线,则实数的值为
A.
B.
C.
D.
8.
若函数上不是单调函数,则实数k的取值范围(
)
A.
B.
C.
D.不存在这样的实数k
9.
10.函数的定义域为,导函数在内的图像如图所示,
则函数在内有极小值点
A.1个
B.2个
C.3个
D.4个
10.已知二次函数的导数为,,对于任意实数都有,则的最小值为
A.
B.
C.
D.
二、填空题(本大题共4个小题,每小题5分,共20分)
11.函数的导数为_________________
12、已知函数在x=1处有极值为10,则f(2)等于____________.
13.函数在区间上的最大值是
14.已知函数在R上有两个极值点,则实数的取值范围是
15.
已知函数是定义在R上的奇函数,,,则不等式
的解集是
三、解答题(本大题共6小题,共80分,解答应写出文字说明,证明过程或演算步骤)
16.
设函数f(x)=sinx-cosx+x+1,0
已知函数.
(Ⅰ)求的值;(Ⅱ)求函数的单调区间.
18.
设函数.
(1)求的单调区间和极值;
(2)若关于的方程有3个不同实根,求实数的取值范围.
(3)已知当恒成立,求实数的取值范围.
19.
已知是函数的一个极值点,其中
(1)求与的关系式;
(2)求的单调区间;
(3)当,函数的图象上任意一点的切线斜率恒大于,求的取值范围。
20.
已知函数
(I)当时,若函数在其定义域内是增函数,求b的取值范围;
(II)若的图象与x轴交于两点,且AB的中点为,求证:
21.
已知函数为自然对数的底数)
(1)求的单调区间,若有最值,请求出最值;
(2)是否存在正常数,使的图象有且只有一个公共点,且在该公共点处有共同的切线?若存在,求出的值,以及公共点坐标和公切线方程;若不存在,请说明理由。
兴国三中高二数学(文)期末复习《导数及其应用》参考答案
一、选择题:
题号
1
2
3
4
5
6
7
8
9
10
答案
B
A
D
A
D
D
D
B
A
C
二、填空题:
11.
;12.
18
13.;
14.;
15.
三、解答题
16.
[解析] f′(x)=cosx+sinx+1=sin(x+)+1 (0
解之得x=π或x=π.
x,f′(x)以及f(x)变化情况如下表:
x
(0,π)
π
(π,π)
π
(π,2π)
f′(x)
+
0
-
0
+
f(x)
递增
π+2
递减
递增
∴f(x)的单调增区间为(0,π)和(π,2π)单调减区间为(π,π).
f极大(x)=f(π)=π+2,f极小(x)=f(π)=.
17.
解:(Ⅰ),所以.
(Ⅱ),
解,得或.
解,得.
所以,为函数的单调增区间,为函数的单调减区间.
18.
解:(1)
…………………1分
∴当,…………………2分
∴的单调递增区间是,单调递减区间是……3分
当;当.…………4分
(2)由(1)可知图象的大致形状及走向(图略)
∴当的图象有3个不同交点,……6分
即当时方程有三解.
…………………………………7分
(3)
∵上恒成立.
…………………………………………9分
令,由二次函数的性质,上是增函数,
∴∴所求的取值范围是……………………………………12分
19.
解:(1)因为是函数的一个极值点.所以
即所以
(2)由(1)知,
当时,有,当为化时,与的变化如下表:
1
-
0
+
0
-
单调递减
极小值
单调递增
极大值
单调递减
故由上表知,当时,在单调递减,在单调递增,在上单调
递减.
(3)由已知得,即又,所以,即
设,其函数图象开口向上,由题意知①式恒成立,所以
解之得所以即的取值范围为
20.(1)由题意:,在上递增,对恒成立,即对恒成立,只需,
,,当且仅当时取“=”,,的取值范围为
(2)由已知得,,两式相减,得:
,
由及,得:
,令,
且,,在上为减函数,
,又,
21.
解:(1)
①当恒成立
上是增函数,F只有一个单调递增区间(0,-∞),没有最值……3分
②当时,,
若,则上单调递减;
若,则上单调递增,
时,有极小值,也是最小值,
即…………6分
所以当时,的单调递减区间为
单调递增区间为,最小值为,无最大值…………7分
(2)方法一,若与的图象有且只有一个公共点,
则方程有且只有一解,所以函数有且只有一个零点…………8分[]
由(1)的结论可知…………10分
此时,
的图象的唯一公共点坐标为
又的图象在点处有共同的切线,
其方程为,即…………13分
综上所述,存在,使的图象有且只有一个公共点,且在该点处的公切线方程为…………14分
方法二:设图象的公共点坐标为,
根据题意得即
由②得,代入①得
从而…………10分
此时由(1)可知
时,
因此除外,再没有其它,使…………13分
故存在,使的图象有且只有一个公共点,且在该公共点处有共同的切线,易求得公共点坐标为,公切线方程为…………14分
第8页(共8页)
