2.1空间点、直线、平面之间的位置关系(新课标A版)
文档属性
| 名称 | 2.1空间点、直线、平面之间的位置关系(新课标A版) |

|
|
| 格式 | zip | ||
| 文件大小 | 491.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-03-29 00:00:00 | ||
图片预览





文档简介
(共91张PPT)
2.1
空间点、直线、平面之间的位置关系
主要内容
2.1.2空间中直线与直线之间的位置关系
2.1.3空间中直线与平面之间的位置关系
2.1.1 平面
2.1.1
平 面
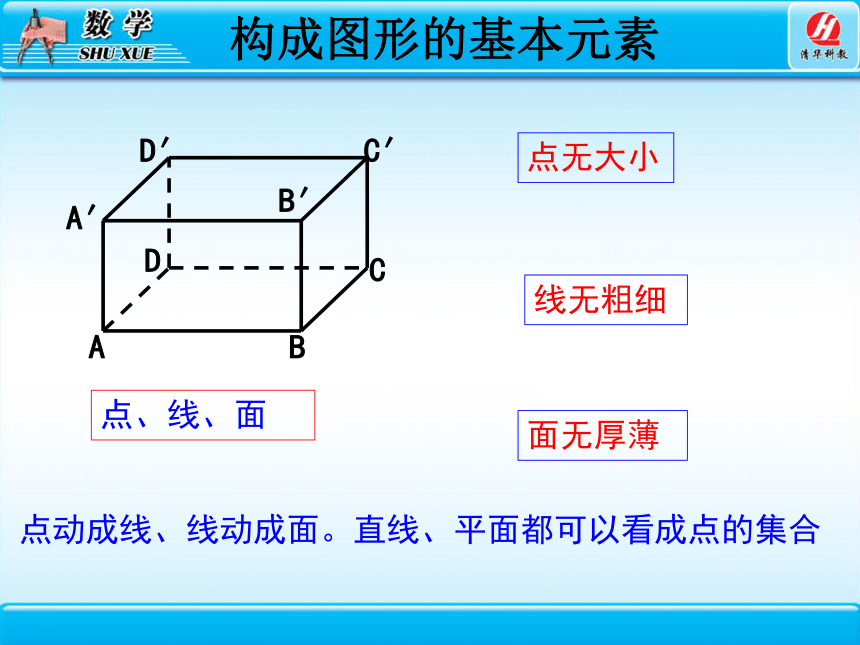
构成图形的基本元素
A′
B′
C′
D′
A
B
C
D
点、线、面
点无大小
线无粗细
面无厚薄
点动成线、线动成面。直线、平面都可以看成点的集合
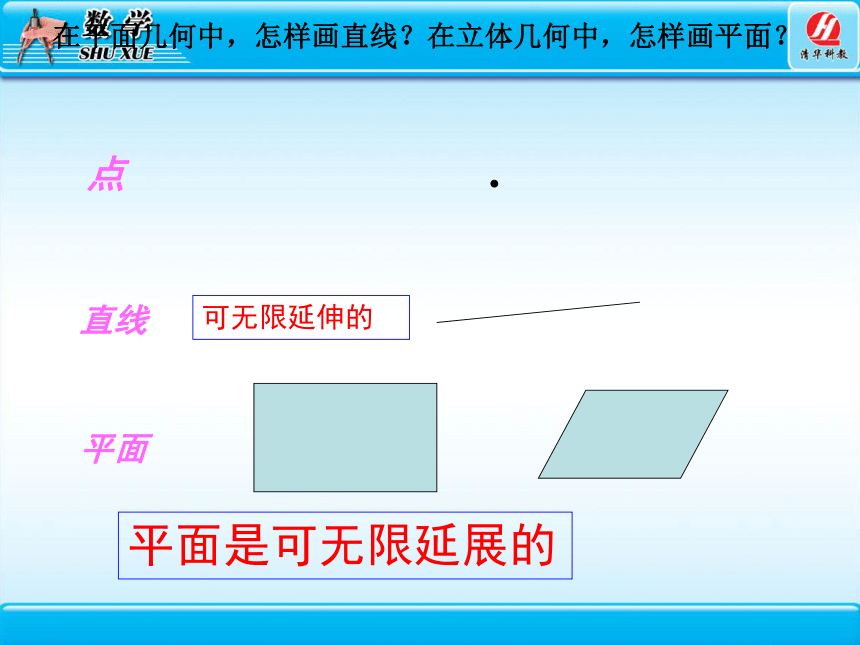
在平面几何中,怎样画直线?在立体几何中,怎样画平面?
点
直线
平面
可无限延伸的
平面是可无限延展的
生活中常见的如黑板、平整的操场、桌面、平静的湖面等等,这些都给我们以平面的印象.请问同学们:你们能举出更多例子吗?
我们不能把一个无限延展的平面在纸上表示出来,通常用平面的一部分表示平面
1、平面的概念
桌面
黑板面
平静的水面
平面的形象
几何里的平面是无限延展的.
平面的表示
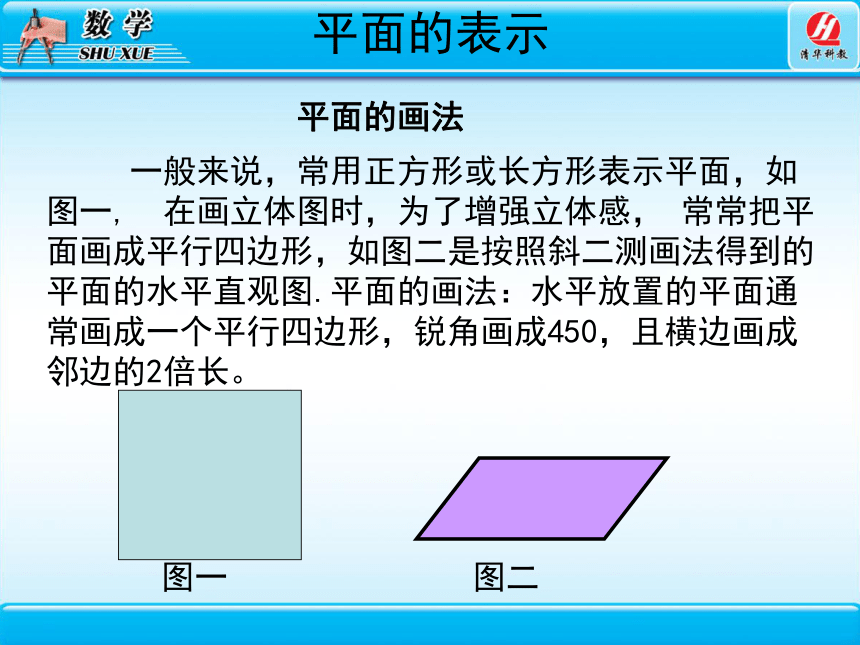
平面的画法
一般来说,常用正方形或长方形表示平面,如图一, 在画立体图时,为了增强立体感, 常常把平面画成平行四边形,如图二是按照斜二测画法得到的平面的水平直观图.平面的画法:水平放置的平面通常画成一个平行四边形,锐角画成450,且横边画成邻边的2倍长。
图一
图二
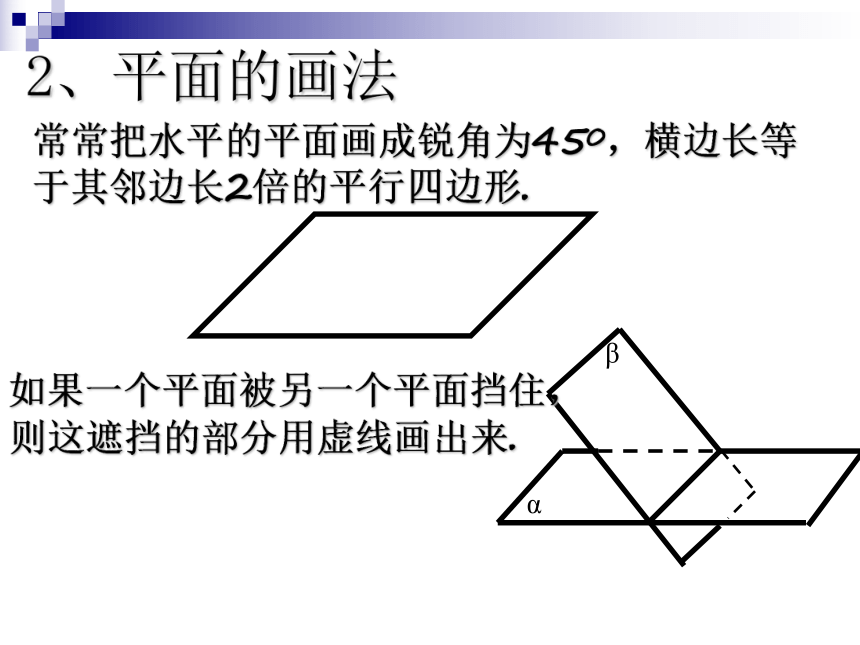
2、平面的画法
常常把水平的平面画成锐角为450,横边长等于其邻边长2倍的平行四边形.
α
β
如果一个平面被另一个平面挡住,
则这遮挡的部分用虚线画出来.
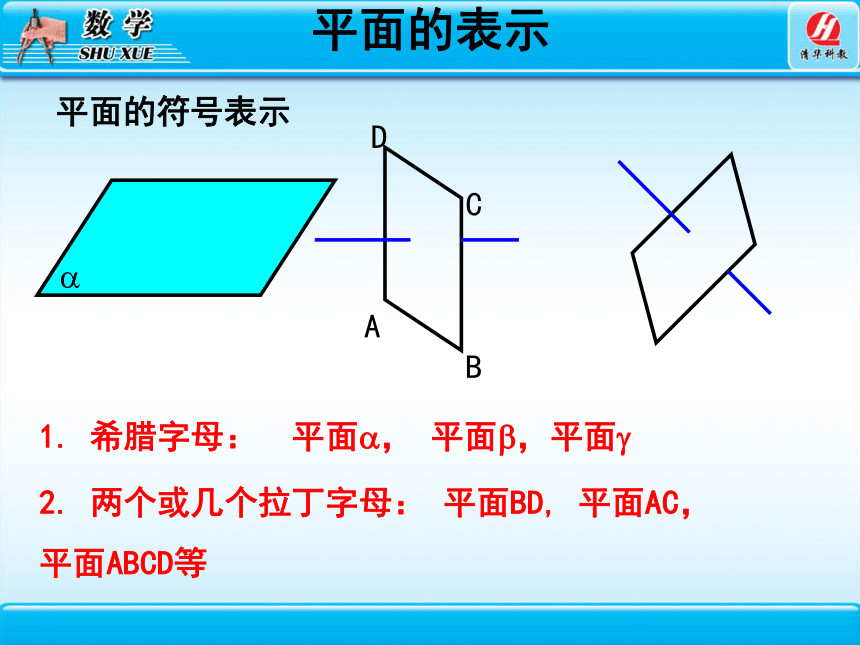
平面的符号表示
1. 希腊字母: 平面 , 平面 ,平面
2. 两个或几个拉丁字母: 平面BD, 平面AC,
平面ABCD等
A
B
C
D
平面的表示
平面的表示
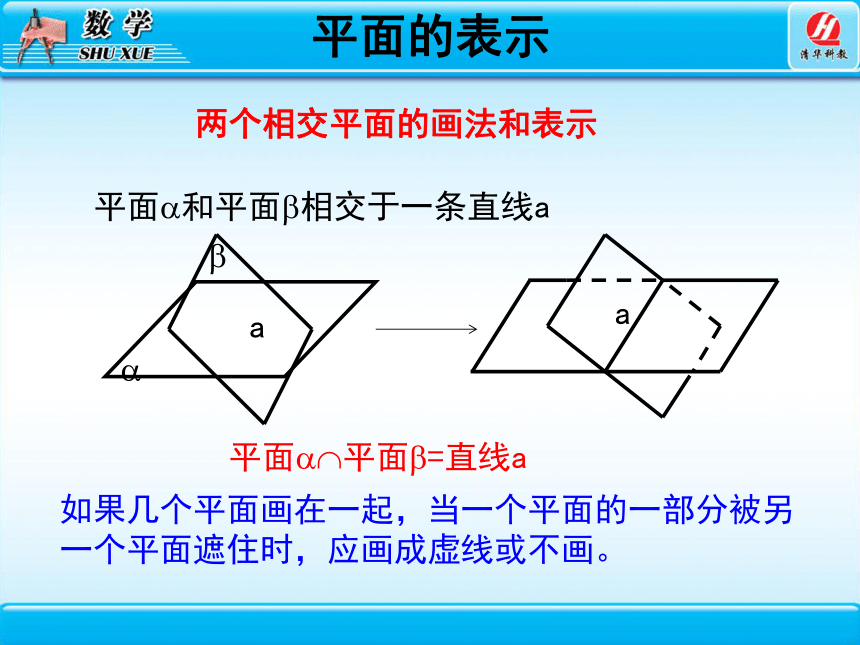
两个相交平面的画法和表示
平面 和平面 相交于一条直线a
a
a
平面 平面 =直线a
如果几个平面画在一起,当一个平面的一部分被另一个平面遮住时,应画成虚线或不画。
平面的表示
直线和平面都可以看成点的集合
“点P在直线l上”,“点A在平面α内”
用集合符号表示 点与直线、点与平面、直线与平面的关系
“点P在直线l 外”,“点A在平面α外”
直线 l 在平面α内,或者说平面α经过直线 l.
直线 l 在平面α外.
P∈L, A∈α
l α
4、点与平面的关系
平面内有无数个点,平面可以看成点的集合.
A
B
α
① 点A在平面α内,记作A∈α
② 点B在平面α外,记作B α
1、判断下列各题的说法正确与否,在正
确的说法的题号后打 ,否则打 :
1、一个平面长 4 米,宽 2 米; ( )
2、平面有边界; ( )
3、一个平面的面积是 25 cm 2; ( )
4、菱形的面积是 4 cm 2; ( )
5、一个平面可以把空间分成两部分. ( )
练习
2、图中平面α与平面β是否为同一平面?
α
β
α
β
α
β
不是
是
不是
练习
3、观察下面两个图形,用模型来说明它
们的位置有什么不同.
练习
如果直线 与平面α有一个公共点,直线 是否在平面α内?如果直线 与平面α有两个公共点呢?
公理1
实际生活中,我们有这样的经验:把一根直尺边缘上的任意两点放到桌面上,可以看到,支持的整个边缘就落到了桌面上。
由上述经验和类似的事实你得到什么启示?
平面的基本性质
.
.
A
B
α
公理1 如果一条直线上的两点在一个平面内,那么这条直线在此平面内.
思考1:如何让一条直线在一个平面内?
作用:为判断直线与平面的位置关系提供依据
集合符号表示
平面经过这条直线
A∈l,B∈l且A∈α,B∈α则 l α
文字语言
图形语言
符号语言
m
B
·
错误
直线m不在平面m内表示为
·
A
·
.
.
作用?
由点、线、面的关系有
直线 在平面α内表示为
公理1:如果一条直线上的两点在一个平面内,
那么这条直线在此平面内.
公理2
生活中,我们常常可以看到这样的现象:三角架可以牢固地支撑照相机或测量用的平板仪等等。
由上述经验和类似的事实你得到什么启示?
平面的基本性质
公理2 过不在一条直线上的三点,有且只有一个平面.
思考2:经过两点可以确定一条直线,那么经过几个点可以确定一个平面呢?
作用:判断几个点共面或直线在同一个平面内
集合符号表示
.
.
.
A
B
C
“不共线的三点确定一个平面”
已知A、B、C三点不共线,则存在惟一平面 ,使得A、B、C
符号表示为:A、B、C三点不共线 => 有且只有一个平面α,使A∈α、B∈α、C∈α.
文字语言
图形语言
符号语言
公理2:过不在一条直线上的三点,
有且只有一个平面.
α
·A
·B
·C
作用?
平面的基本性质
思考3:如果两个平面有一个公共点,那么还会有其它公共点吗?如果有这些公共点有什么特征?
公理3 如果两个不重合的平面有一个公共点,那么它们有且只有一条过该点的公共直线.
P
作用:判断两个平面位置关系的基本依据
符号表示为:P∈α∩β =>α∩β=L,且P∈L
文字语言
图形语言
符号语言
公理3:如果两个不重合的平面有一个公共点,
那么它们有且只有一条过该点的公共直线.
α
β
·
P
作用?
把三角板的一个角立在课桌面上,三角板所在平面
与桌面所在平面是否只相交于一点?为什么?
例题
例1 如图,用符号表示下列图形中点、直线、平面之间的位置关系.
A
B
β
α
a
l
(1)
a
b
P
l
β
α
(2)
解:1) A ,B , =l,a =A,a =B
2) a ,b , =l,a l=P, b l=P, a b=P
P
a
例2:已知直线a,和点P,P a,求证经过点P和直线a有且只有一个平面.
证明:点P是直线a外一点,在直线a上任取两点
A、B,根据公理2,经过不共线的三点P、A、B
有一个平面α。
因为点A、B在平面α内,所以根据公理1,
直线a在平面α内,即平面α是经过直线a和点P
的平面。
又因为点A、B在直线a上,所以任何经过点P
和直线a的平面一定经过点P、A、B。
于是再根据公理2,经过不共线的三点P、A、B
的有且只有一个平面,所以经过点P和直线a有且只
有一个平面.
探究问题
根据公理1探究直线与平面的各种位置关系.
根据公理2探究两条相交直线或平行直线确定一个平面的合理性.
根据公理3探究平面与平面的各种位置关系.
③四条线段顺次首尾连接,所得的图形一定是平面图形吗?
为什么?
练习
①为什么有的自行车后轮旁只安装一只撑脚?
②三角形、梯形是否一定是平面图形?为什么?
④用符号表示下列语句,并画出图形:
⑴点A在平面α内,点B在平面α外;
⑵直线 在平面α内,直线m不在平面α内;
⑶平面α和β相交于直线 ;
⑷直线 经过平面α外一点P和平面α内一点Q ;
⑸直线 是平面α和β的交线,直线m在平面α内,
和m相交于点P.
小结
1.平面的表示:概念、图形、符号等
2.平面的基本性质
公理1
公理2
公理3
3.判断共面的方法
作业
P43 练习1,2,34
P51 习题A组 1,2
2.1.2
空间中直线与直线之间的位置关系
两条直线的位置关系
思考1:同一平面内两条直线有几种位置关系?空间中的两条直线呢?
C
1)教室内日光灯管所在直线与黑板左右两侧所在直线的位置关系如何?
2)天安门广场上,旗杆所在直线与长安街所在直线的位置关系如何?
两条直线的位置关系
如图, 长方体ABCD-A′B′C′D′中,线段A′B所在直线分别与线段CD′所在直线,线段BC所在直线,线段CD所在直线的位置关系如何
C
B'
C'
A'
D'
B
A
D
观察
两条直线的位置关系
定义 不同在任何一个平面内的两条直线叫做异面直线.
b
a
a
b
异面直线的图示
两条直线的位置关系
A. 空间中既不平行又不相交的两条直线;
B. 平面内的一条直线和这平面外的一条直线;
C. 分别在不同平面内的两条直线;
D. 不在同一个平面内的两条直线;
E. 不同在任何一个平面内的两条直线.
关于异面直线的定义,你认为下列哪个说法最合适?
问题
两条直线的位置关系
空间中的直线与直线之间有三种位置关系:
相交直线:
平行直线:
共面直线
异面直线:
不同在任何一个平面内,没有公共点
同一平面内,有且只有一个公共点;
同一平面内,没有公共点;
如图是一个正方体的表面展开图,如果将它还原为正方体,那么AB,CD,EF,GH这四条线段所在直线是异面直线的有多少对
探究
F
A
H
G
E
D
C
B
C
D
B
A
E
F
G
H
直线EF 和直线HG
直线AB 和直线CD
直线AB 和直线HG
答:3对
平行直线
如图, 在长方体ABCD—A′B′C′D′中, BB′∥AA′,DD′∥AA′,那么BB′与DD′平行吗
C
B'
C'
A'
D'
B
A
D
观察
答:平行
平行直线
公理4 平行于同一直线的两条直线互相平行.
空间中的平行线具有传递性
如果a//b,b//c,那么a//c
A
F
E
D
C
B
A
B
C
D
E
F
三条平行线共面
三条平行线不共面
平行直线
已知三条直线两两平行,任取两条直线能确定一个平面,问这三条直线能确定几个平面?
A
F
E
D
C
B
A
B
C
D
E
F
三条平行线共面
三条平行线不共面
问题
平行直线
例2 如图,空间四边形ABCD中,E,F,G,H分别是AB,BC,CD,DA的中点.
求证:四边形EFGH是平行四边形.
F
G
D
A
E
B
C
H
所以
,且
同理
,且
因为
,且
所以 四边形EFGH 是平行四边形.
证明:连接BD,
因为 EH是 的中位线,
在上例中,如果再加上条件AC=BD,那么四边形EFGH 是什么图形?
探究
答:四边形EFGH是菱形
F
G
D
A
E
B
C
H
等角定理
在平面上,我们容易证明“如果一个角的两边和另一个角的两边分别平行, 那么这两个角相等或互补”.空间中,结论是否仍然成立?
思考1
如图,四棱柱ABCD--A′B′C′D′的底面是平行四边形,∠ADC与∠A′D′C′, ∠ADC与∠B′A′D′的两边分别对应平行,这两组角的大小关系如何
思考2:
B
A
D
C
A'
B'
D'
C'
B
A
D
C
A'
B'
D'
C'
∠ADC=∠A′D′C′
∠ADC+∠B′A′D′=1800
如图,在空间中AB// A′B′,AC// A′C′,你能证明∠BAC与∠B′A′C′ 相等吗?
思考3
B
C
A
B
C
A
E
E
D
D
等角定理
定理 空间中如果两个角的两边分别对应平行,那么这两个角相等或互补.
等角定理:空间中如果两个角的两边分别对应平行且方向相同,那么这两个角相等.
异面直线所成的角
复习:
1、异面直线的概念:
我们把___________________________________叫做异面直线
2、空间两条直线的位置关系有且只有__种:____________
3、平行公理4:________________________________
。(平行线的传递性)
4、等角定理:__________________________
___________________________
不同在任一平面内的两条直线
三
相交、平行、异面。
平行于同一条直线的两直线互相平行
空间中如果两个角的两边分别平行,那么这两个角相等或互补。
若a∥c,b∥c 则a∥b
其特点是既不相交也不平行
问题1:正方体ABCD—A1B1C1D1中,E为BC的中点,判断直线A1C1、B1C1、C1E、C1C与直线AB的位置关系。
A
B
C
D
A
B
C
D
1
1
1
1
E
说明:从位置关系来看,同为异面直线,但它们的相对位置却是不同的,说明仅用“异面”来考虑异面直线间的相对位置是不够的。
问题2:用什么来刻划两条异面直线的相对位置呢?
距离和角
问题3:一张纸中画有两条能相交的直线a、b(但交点在纸外)现给你一副三角板和量角器,限定不许拼接纸片,不许延长纸上的线段,问如何量出a、b所成角的大小?其理论依据是什么?
a
b
问题4:能否将上述结论推广到空间两直线?
b’
异面直线所成的角
a
b
思考
在同一平面内两条相交直线形成四个角,常取较小的一组角来度量这两条直线的位置关系,这个角叫做两条直线的夹角.在空间中怎样度量两条异面直线的位置关系呢?
a
b
平面内两条相交直线
空间中两条异面直线
O
已知两条异面直线a,b,经过空间任一点O作直线 ,把 与 所成的锐角(或直角)叫做异面直线a与b所成的角.
O
异面直线所成的角
我们规定两条平行直线的夹角为0°,那么两条异面直线所成的角的取值范围是什么?
如果两条异面直线所成角为900,那么这两条直线垂直.
探究
记直线a垂直于b为:a b
异面直线所成角的定义:
直线a、b是异面直线,经过空间任意一点O,分别引直线a’//a,b’//b,把直线a’和b’所成的锐角(或直角)叫直线a和b所成的角。
思考:两条异面直线所成角的大小是否随空间任意点O位置的不同而改变?
点O可任选,一般取特殊位置,如线段的中点或端点等。
a
b
a’
O
O’
O1
a’
b’
b1
a1
探究:
(1)如果两条平行直线中的一条与某一条直线垂直,那么,另一条直线是否也与这条直线垂直
(2)垂直于同一条直线的两条直线是否平行
即a∥b,若a⊥c,则b⊥c
下面我们来探究更一般的角的问题
a
b
c
异面直线所成的角
探究
(1)在长方体 中,有没有两条棱所在的直线是相互垂直的异面直线?
(2)如果两条平行直线中的一条与某一条直线垂直,那么,另一条直线是否也与这条直线垂直?
(3)垂直于同一条直线的两条直线是否平行?
如:
等.
垂直
不一定,如上图的立方体中
直线AB与BC相交,
异面直线所成的角
例3 已知正方体 .
(1)哪些棱所在直线与直线 是异面直线?
(2)直线 和 的夹角是多少?
(3)哪些棱所在的直线与直线 垂直?
解:(1)由异面直线的定义可知,
棱 所在的直线分别与直线 是异面直线.
(3)直线
分别与直线 垂直.
(2)由 可知,
为
异面直线 与 的夹角, ,
所以 与 的夹角为 .
在如图所示的长方体中,AB= ,且
AA1=1,求直线BA1和CD所成角的度数.
30O
练习1
巩固、提高
例1、在正方体ABCD—A1B1C1D1中,求:
(1)A1B与CC1所成的角;
D
1
A
B
C
D
A
B
C
1
1
1
分析:
(1)∵B1B // CC1
∴ ∠A1BB1为A1B与CC1所成的角
在△A1BB1中,A1B1=BB1;
∴ ∠A1BB1=45o
∴A1B与CC1所成的角为45o
--------找
--------证
--------算
--------答
巩固、提高
例1、在正方体ABCD—A1B1C1D1中,求:
(1)A1B与CC1所成的角;
口答
(2) A1B1与C1C所成的角;
(3)A1C1与BC所成的角;
(4)A1C1与D1C所成的角。
A
B
C
D
A
B
C
D
1
1
1
1
(2)∠A1B1B=90o
(3)∠A1C1B1=45o
(4)∠BA1C1=600
小结二:求异面直线所成的角一般要有四个步骤:
简记为“作(找)——证——算——答”。
(1)作图:作(找)出所求的角及题中涉及的有关图形等;
(2)证明:证明所给图形是符合题设要求的;
(3)计算:一般是利用解三角形计算得出结果。
(4)结论。
小结一:这种求法就是利用平移将两条异面直线转化到同一个三角形中,通过解三角形来求解。把这种方法叫做——平移法,其基本解题思路是“异面化共面,认定再计算”,
如图,在四面体ABCD中,E,F分别是棱AD,BC上的点,且 ,已知AB=CD=3,
, 求异面直线AB和CD所成的角.
A
F
E
D
C
B
练习2
变式一:
(07福建卷)如图,在正方体ABCD-A1B1C1D1中,E、F、G、H分别为AA1、AB、BB1、B1C1的中点,则异面直线EF与GH所成的角等于( )
A.45° B.60° C.90° D.120°
步骤 “作(找)——证——算——答”
A
B
C
D
A
B
C
D
1
1
1
1
E
G
F
H
解:连接A1B,BC1,A1C1
∵A1B // EF,BC1 // GH
∴∠A1B C1为EF1与GH所成的角
在三角形A1BC1中,A1B= BC1= A1C1
∴∠A1B C1=60°
∴异面直线EF与GH所成的角等于60°
n直线相交最多有几个交点?
练习3
课堂小结:
1、异面直线所成角的定义、范围及其求解。在求解中,一定要紧扣定义中点O的任意性,恰当选择。
2、计算角的大小,要遵循“作——证——算——答”四步骤。
3、求解异面直线所成的角的方法是“平移法”,也即“化异面为共面”,“化空间为平面”,它突出体现了转化化归的数学思想与方法。在计算的过程中,若直观性不强,则要懂得将平面图形单独分离,有利于计算的直观性。作答时要注意异面直线所成的角的范围的约束。
本节小结
(1)空间直线的三种位置关系.
(2)平行线的传递性.
(3)等角定理.
(4)异面直线所成的角.
基本知识
基本方法
把空间中问题通过平移转化为平面问题.
课后作业:
课本第48页练习第2题。
补充:
1、空间四边形ABCD中,PR分别是AB、CD的中点,且PR= ,AC=BD=2,求AC与BD所成的角。
2、正方体ABCD—A1B1C1D1中,M为AB的中点,N为BB1的中点,求A1M与C1N所成角的余弦值。
D
A
B
C
R
P
A
B
C
D
A
B
C
D
1
1
1
1
作业
P48 练习1,2
P51 -52习题2.1 A组 3,4(1)(2)(3)(6),5,6,
B组1
2.1.3
空间中直线与平面之间的位置关系
主要内容
直线与平面的位置关系
直线在平面内
直线与平面相交
直线与平面平行
直线与平面
思考?
1)一支铅笔所在的直线与一个作业本所在的平面,可能有几种关系?
2)如图,线段A’B所在直线与长方体ABCD-A’B’C’D’的六个面所在平面有几种位置关系?
C
B'
C'
A'
D'
B
A
D
直线与平面
直线和平面的位置关系有且只有三种
(1)直线在平面内
有无数个公共点
a
记为:a
直线与平面
(2)直线与平面相交
有且只有一个公共点
a
记为:a =A
A
直线与平面
(3)直线与平面平行
没有公共点
a
记为:a//
直线与平面
直线与平面相交或平行的情况统称为直线在平面外
记为:a
a
a//
a
a =A
A
或
直线与平面
例1. 下列命题中正确的个数是 ( )
1)若直线 l 上有无数个点不在平面 内,则 l//
2) 若直线 l 与平面 平行,则 l 与平面 内的任意一条直线都平行
3)如果两条平行直线中的一条与一个平面平行,那么另一条也与这个平面平行
4)若直线 l与平面 平行,则 l与平面 内的任意一条直线都没有公共点.
(A) 0 (B) 1 (C) 2 (D) 3
B
主要内容
直线与平面的位置关系
直线在平面内
直线与平面相交
直线与平面平行
作业
P49 练习
P51-53 习题2.1A组 4(4)(5) B 2,3
平面与平面之间的位置关系
2.1.4
平面与平面之间的位置关系
思考
(1)拿出两本书,看作两个平面,上下、左右移动和翻转,它们之间的位置关系有几种?
(2)如图,围成长方体ABCD-A′B′C′D′的六个面,两两之间的位置关系有几种?
C
B'
C'
A'
D'
B
A
D
两个平面的位置关系
两个平面的位置关系有且只有两种
①两个平面平行——没有公共点
②两个平面相交——有一条公共直线.
分类的依据是什么?
公理3 如果两个不重合的平面有一个公共点,那么它们有且只有一条过该点的公共直线.
两个平面平行或相交的画法及表示
//
m
=m
已知平面 ,直线a、b,且 // ,a ,b ,则直线a与直线b具有怎样的位置关系?
探究1
a
b
答:平行或异面
探究2
α
β
γ
a
b
l
b
α
β
γ
a
l
相交于一条交线
三条交线
三条交线
如果三个平面两两相交,那么它们的交线有多少条?画出图形表示你的结论.
一个平面可以把空间分成几个部分?
两个平面可以把空间分成几个部分?
三个平面可以把空间分成几个部分?
探究3
小结
平面与平面的位置关系
平面与平面相交
平面与平面平行
作业
P50 练习
P52 习题2.1 A组7,8
2.1
空间点、直线、平面之间的位置关系
主要内容
2.1.2空间中直线与直线之间的位置关系
2.1.3空间中直线与平面之间的位置关系
2.1.1 平面
2.1.1
平 面
构成图形的基本元素
A′
B′
C′
D′
A
B
C
D
点、线、面
点无大小
线无粗细
面无厚薄
点动成线、线动成面。直线、平面都可以看成点的集合
在平面几何中,怎样画直线?在立体几何中,怎样画平面?
点
直线
平面
可无限延伸的
平面是可无限延展的
生活中常见的如黑板、平整的操场、桌面、平静的湖面等等,这些都给我们以平面的印象.请问同学们:你们能举出更多例子吗?
我们不能把一个无限延展的平面在纸上表示出来,通常用平面的一部分表示平面
1、平面的概念
桌面
黑板面
平静的水面
平面的形象
几何里的平面是无限延展的.
平面的表示
平面的画法
一般来说,常用正方形或长方形表示平面,如图一, 在画立体图时,为了增强立体感, 常常把平面画成平行四边形,如图二是按照斜二测画法得到的平面的水平直观图.平面的画法:水平放置的平面通常画成一个平行四边形,锐角画成450,且横边画成邻边的2倍长。
图一
图二
2、平面的画法
常常把水平的平面画成锐角为450,横边长等于其邻边长2倍的平行四边形.
α
β
如果一个平面被另一个平面挡住,
则这遮挡的部分用虚线画出来.
平面的符号表示
1. 希腊字母: 平面 , 平面 ,平面
2. 两个或几个拉丁字母: 平面BD, 平面AC,
平面ABCD等
A
B
C
D
平面的表示
平面的表示
两个相交平面的画法和表示
平面 和平面 相交于一条直线a
a
a
平面 平面 =直线a
如果几个平面画在一起,当一个平面的一部分被另一个平面遮住时,应画成虚线或不画。
平面的表示
直线和平面都可以看成点的集合
“点P在直线l上”,“点A在平面α内”
用集合符号表示 点与直线、点与平面、直线与平面的关系
“点P在直线l 外”,“点A在平面α外”
直线 l 在平面α内,或者说平面α经过直线 l.
直线 l 在平面α外.
P∈L, A∈α
l α
4、点与平面的关系
平面内有无数个点,平面可以看成点的集合.
A
B
α
① 点A在平面α内,记作A∈α
② 点B在平面α外,记作B α
1、判断下列各题的说法正确与否,在正
确的说法的题号后打 ,否则打 :
1、一个平面长 4 米,宽 2 米; ( )
2、平面有边界; ( )
3、一个平面的面积是 25 cm 2; ( )
4、菱形的面积是 4 cm 2; ( )
5、一个平面可以把空间分成两部分. ( )
练习
2、图中平面α与平面β是否为同一平面?
α
β
α
β
α
β
不是
是
不是
练习
3、观察下面两个图形,用模型来说明它
们的位置有什么不同.
练习
如果直线 与平面α有一个公共点,直线 是否在平面α内?如果直线 与平面α有两个公共点呢?
公理1
实际生活中,我们有这样的经验:把一根直尺边缘上的任意两点放到桌面上,可以看到,支持的整个边缘就落到了桌面上。
由上述经验和类似的事实你得到什么启示?
平面的基本性质
.
.
A
B
α
公理1 如果一条直线上的两点在一个平面内,那么这条直线在此平面内.
思考1:如何让一条直线在一个平面内?
作用:为判断直线与平面的位置关系提供依据
集合符号表示
平面经过这条直线
A∈l,B∈l且A∈α,B∈α则 l α
文字语言
图形语言
符号语言
m
B
·
错误
直线m不在平面m内表示为
·
A
·
.
.
作用?
由点、线、面的关系有
直线 在平面α内表示为
公理1:如果一条直线上的两点在一个平面内,
那么这条直线在此平面内.
公理2
生活中,我们常常可以看到这样的现象:三角架可以牢固地支撑照相机或测量用的平板仪等等。
由上述经验和类似的事实你得到什么启示?
平面的基本性质
公理2 过不在一条直线上的三点,有且只有一个平面.
思考2:经过两点可以确定一条直线,那么经过几个点可以确定一个平面呢?
作用:判断几个点共面或直线在同一个平面内
集合符号表示
.
.
.
A
B
C
“不共线的三点确定一个平面”
已知A、B、C三点不共线,则存在惟一平面 ,使得A、B、C
符号表示为:A、B、C三点不共线 => 有且只有一个平面α,使A∈α、B∈α、C∈α.
文字语言
图形语言
符号语言
公理2:过不在一条直线上的三点,
有且只有一个平面.
α
·A
·B
·C
作用?
平面的基本性质
思考3:如果两个平面有一个公共点,那么还会有其它公共点吗?如果有这些公共点有什么特征?
公理3 如果两个不重合的平面有一个公共点,那么它们有且只有一条过该点的公共直线.
P
作用:判断两个平面位置关系的基本依据
符号表示为:P∈α∩β =>α∩β=L,且P∈L
文字语言
图形语言
符号语言
公理3:如果两个不重合的平面有一个公共点,
那么它们有且只有一条过该点的公共直线.
α
β
·
P
作用?
把三角板的一个角立在课桌面上,三角板所在平面
与桌面所在平面是否只相交于一点?为什么?
例题
例1 如图,用符号表示下列图形中点、直线、平面之间的位置关系.
A
B
β
α
a
l
(1)
a
b
P
l
β
α
(2)
解:1) A ,B , =l,a =A,a =B
2) a ,b , =l,a l=P, b l=P, a b=P
P
a
例2:已知直线a,和点P,P a,求证经过点P和直线a有且只有一个平面.
证明:点P是直线a外一点,在直线a上任取两点
A、B,根据公理2,经过不共线的三点P、A、B
有一个平面α。
因为点A、B在平面α内,所以根据公理1,
直线a在平面α内,即平面α是经过直线a和点P
的平面。
又因为点A、B在直线a上,所以任何经过点P
和直线a的平面一定经过点P、A、B。
于是再根据公理2,经过不共线的三点P、A、B
的有且只有一个平面,所以经过点P和直线a有且只
有一个平面.
探究问题
根据公理1探究直线与平面的各种位置关系.
根据公理2探究两条相交直线或平行直线确定一个平面的合理性.
根据公理3探究平面与平面的各种位置关系.
③四条线段顺次首尾连接,所得的图形一定是平面图形吗?
为什么?
练习
①为什么有的自行车后轮旁只安装一只撑脚?
②三角形、梯形是否一定是平面图形?为什么?
④用符号表示下列语句,并画出图形:
⑴点A在平面α内,点B在平面α外;
⑵直线 在平面α内,直线m不在平面α内;
⑶平面α和β相交于直线 ;
⑷直线 经过平面α外一点P和平面α内一点Q ;
⑸直线 是平面α和β的交线,直线m在平面α内,
和m相交于点P.
小结
1.平面的表示:概念、图形、符号等
2.平面的基本性质
公理1
公理2
公理3
3.判断共面的方法
作业
P43 练习1,2,34
P51 习题A组 1,2
2.1.2
空间中直线与直线之间的位置关系
两条直线的位置关系
思考1:同一平面内两条直线有几种位置关系?空间中的两条直线呢?
C
1)教室内日光灯管所在直线与黑板左右两侧所在直线的位置关系如何?
2)天安门广场上,旗杆所在直线与长安街所在直线的位置关系如何?
两条直线的位置关系
如图, 长方体ABCD-A′B′C′D′中,线段A′B所在直线分别与线段CD′所在直线,线段BC所在直线,线段CD所在直线的位置关系如何
C
B'
C'
A'
D'
B
A
D
观察
两条直线的位置关系
定义 不同在任何一个平面内的两条直线叫做异面直线.
b
a
a
b
异面直线的图示
两条直线的位置关系
A. 空间中既不平行又不相交的两条直线;
B. 平面内的一条直线和这平面外的一条直线;
C. 分别在不同平面内的两条直线;
D. 不在同一个平面内的两条直线;
E. 不同在任何一个平面内的两条直线.
关于异面直线的定义,你认为下列哪个说法最合适?
问题
两条直线的位置关系
空间中的直线与直线之间有三种位置关系:
相交直线:
平行直线:
共面直线
异面直线:
不同在任何一个平面内,没有公共点
同一平面内,有且只有一个公共点;
同一平面内,没有公共点;
如图是一个正方体的表面展开图,如果将它还原为正方体,那么AB,CD,EF,GH这四条线段所在直线是异面直线的有多少对
探究
F
A
H
G
E
D
C
B
C
D
B
A
E
F
G
H
直线EF 和直线HG
直线AB 和直线CD
直线AB 和直线HG
答:3对
平行直线
如图, 在长方体ABCD—A′B′C′D′中, BB′∥AA′,DD′∥AA′,那么BB′与DD′平行吗
C
B'
C'
A'
D'
B
A
D
观察
答:平行
平行直线
公理4 平行于同一直线的两条直线互相平行.
空间中的平行线具有传递性
如果a//b,b//c,那么a//c
A
F
E
D
C
B
A
B
C
D
E
F
三条平行线共面
三条平行线不共面
平行直线
已知三条直线两两平行,任取两条直线能确定一个平面,问这三条直线能确定几个平面?
A
F
E
D
C
B
A
B
C
D
E
F
三条平行线共面
三条平行线不共面
问题
平行直线
例2 如图,空间四边形ABCD中,E,F,G,H分别是AB,BC,CD,DA的中点.
求证:四边形EFGH是平行四边形.
F
G
D
A
E
B
C
H
所以
,且
同理
,且
因为
,且
所以 四边形EFGH 是平行四边形.
证明:连接BD,
因为 EH是 的中位线,
在上例中,如果再加上条件AC=BD,那么四边形EFGH 是什么图形?
探究
答:四边形EFGH是菱形
F
G
D
A
E
B
C
H
等角定理
在平面上,我们容易证明“如果一个角的两边和另一个角的两边分别平行, 那么这两个角相等或互补”.空间中,结论是否仍然成立?
思考1
如图,四棱柱ABCD--A′B′C′D′的底面是平行四边形,∠ADC与∠A′D′C′, ∠ADC与∠B′A′D′的两边分别对应平行,这两组角的大小关系如何
思考2:
B
A
D
C
A'
B'
D'
C'
B
A
D
C
A'
B'
D'
C'
∠ADC=∠A′D′C′
∠ADC+∠B′A′D′=1800
如图,在空间中AB// A′B′,AC// A′C′,你能证明∠BAC与∠B′A′C′ 相等吗?
思考3
B
C
A
B
C
A
E
E
D
D
等角定理
定理 空间中如果两个角的两边分别对应平行,那么这两个角相等或互补.
等角定理:空间中如果两个角的两边分别对应平行且方向相同,那么这两个角相等.
异面直线所成的角
复习:
1、异面直线的概念:
我们把___________________________________叫做异面直线
2、空间两条直线的位置关系有且只有__种:____________
3、平行公理4:________________________________
。(平行线的传递性)
4、等角定理:__________________________
___________________________
不同在任一平面内的两条直线
三
相交、平行、异面。
平行于同一条直线的两直线互相平行
空间中如果两个角的两边分别平行,那么这两个角相等或互补。
若a∥c,b∥c 则a∥b
其特点是既不相交也不平行
问题1:正方体ABCD—A1B1C1D1中,E为BC的中点,判断直线A1C1、B1C1、C1E、C1C与直线AB的位置关系。
A
B
C
D
A
B
C
D
1
1
1
1
E
说明:从位置关系来看,同为异面直线,但它们的相对位置却是不同的,说明仅用“异面”来考虑异面直线间的相对位置是不够的。
问题2:用什么来刻划两条异面直线的相对位置呢?
距离和角
问题3:一张纸中画有两条能相交的直线a、b(但交点在纸外)现给你一副三角板和量角器,限定不许拼接纸片,不许延长纸上的线段,问如何量出a、b所成角的大小?其理论依据是什么?
a
b
问题4:能否将上述结论推广到空间两直线?
b’
异面直线所成的角
a
b
思考
在同一平面内两条相交直线形成四个角,常取较小的一组角来度量这两条直线的位置关系,这个角叫做两条直线的夹角.在空间中怎样度量两条异面直线的位置关系呢?
a
b
平面内两条相交直线
空间中两条异面直线
O
已知两条异面直线a,b,经过空间任一点O作直线 ,把 与 所成的锐角(或直角)叫做异面直线a与b所成的角.
O
异面直线所成的角
我们规定两条平行直线的夹角为0°,那么两条异面直线所成的角的取值范围是什么?
如果两条异面直线所成角为900,那么这两条直线垂直.
探究
记直线a垂直于b为:a b
异面直线所成角的定义:
直线a、b是异面直线,经过空间任意一点O,分别引直线a’//a,b’//b,把直线a’和b’所成的锐角(或直角)叫直线a和b所成的角。
思考:两条异面直线所成角的大小是否随空间任意点O位置的不同而改变?
点O可任选,一般取特殊位置,如线段的中点或端点等。
a
b
a’
O
O’
O1
a’
b’
b1
a1
探究:
(1)如果两条平行直线中的一条与某一条直线垂直,那么,另一条直线是否也与这条直线垂直
(2)垂直于同一条直线的两条直线是否平行
即a∥b,若a⊥c,则b⊥c
下面我们来探究更一般的角的问题
a
b
c
异面直线所成的角
探究
(1)在长方体 中,有没有两条棱所在的直线是相互垂直的异面直线?
(2)如果两条平行直线中的一条与某一条直线垂直,那么,另一条直线是否也与这条直线垂直?
(3)垂直于同一条直线的两条直线是否平行?
如:
等.
垂直
不一定,如上图的立方体中
直线AB与BC相交,
异面直线所成的角
例3 已知正方体 .
(1)哪些棱所在直线与直线 是异面直线?
(2)直线 和 的夹角是多少?
(3)哪些棱所在的直线与直线 垂直?
解:(1)由异面直线的定义可知,
棱 所在的直线分别与直线 是异面直线.
(3)直线
分别与直线 垂直.
(2)由 可知,
为
异面直线 与 的夹角, ,
所以 与 的夹角为 .
在如图所示的长方体中,AB= ,且
AA1=1,求直线BA1和CD所成角的度数.
30O
练习1
巩固、提高
例1、在正方体ABCD—A1B1C1D1中,求:
(1)A1B与CC1所成的角;
D
1
A
B
C
D
A
B
C
1
1
1
分析:
(1)∵B1B // CC1
∴ ∠A1BB1为A1B与CC1所成的角
在△A1BB1中,A1B1=BB1;
∴ ∠A1BB1=45o
∴A1B与CC1所成的角为45o
--------找
--------证
--------算
--------答
巩固、提高
例1、在正方体ABCD—A1B1C1D1中,求:
(1)A1B与CC1所成的角;
口答
(2) A1B1与C1C所成的角;
(3)A1C1与BC所成的角;
(4)A1C1与D1C所成的角。
A
B
C
D
A
B
C
D
1
1
1
1
(2)∠A1B1B=90o
(3)∠A1C1B1=45o
(4)∠BA1C1=600
小结二:求异面直线所成的角一般要有四个步骤:
简记为“作(找)——证——算——答”。
(1)作图:作(找)出所求的角及题中涉及的有关图形等;
(2)证明:证明所给图形是符合题设要求的;
(3)计算:一般是利用解三角形计算得出结果。
(4)结论。
小结一:这种求法就是利用平移将两条异面直线转化到同一个三角形中,通过解三角形来求解。把这种方法叫做——平移法,其基本解题思路是“异面化共面,认定再计算”,
如图,在四面体ABCD中,E,F分别是棱AD,BC上的点,且 ,已知AB=CD=3,
, 求异面直线AB和CD所成的角.
A
F
E
D
C
B
练习2
变式一:
(07福建卷)如图,在正方体ABCD-A1B1C1D1中,E、F、G、H分别为AA1、AB、BB1、B1C1的中点,则异面直线EF与GH所成的角等于( )
A.45° B.60° C.90° D.120°
步骤 “作(找)——证——算——答”
A
B
C
D
A
B
C
D
1
1
1
1
E
G
F
H
解:连接A1B,BC1,A1C1
∵A1B // EF,BC1 // GH
∴∠A1B C1为EF1与GH所成的角
在三角形A1BC1中,A1B= BC1= A1C1
∴∠A1B C1=60°
∴异面直线EF与GH所成的角等于60°
n直线相交最多有几个交点?
练习3
课堂小结:
1、异面直线所成角的定义、范围及其求解。在求解中,一定要紧扣定义中点O的任意性,恰当选择。
2、计算角的大小,要遵循“作——证——算——答”四步骤。
3、求解异面直线所成的角的方法是“平移法”,也即“化异面为共面”,“化空间为平面”,它突出体现了转化化归的数学思想与方法。在计算的过程中,若直观性不强,则要懂得将平面图形单独分离,有利于计算的直观性。作答时要注意异面直线所成的角的范围的约束。
本节小结
(1)空间直线的三种位置关系.
(2)平行线的传递性.
(3)等角定理.
(4)异面直线所成的角.
基本知识
基本方法
把空间中问题通过平移转化为平面问题.
课后作业:
课本第48页练习第2题。
补充:
1、空间四边形ABCD中,PR分别是AB、CD的中点,且PR= ,AC=BD=2,求AC与BD所成的角。
2、正方体ABCD—A1B1C1D1中,M为AB的中点,N为BB1的中点,求A1M与C1N所成角的余弦值。
D
A
B
C
R
P
A
B
C
D
A
B
C
D
1
1
1
1
作业
P48 练习1,2
P51 -52习题2.1 A组 3,4(1)(2)(3)(6),5,6,
B组1
2.1.3
空间中直线与平面之间的位置关系
主要内容
直线与平面的位置关系
直线在平面内
直线与平面相交
直线与平面平行
直线与平面
思考?
1)一支铅笔所在的直线与一个作业本所在的平面,可能有几种关系?
2)如图,线段A’B所在直线与长方体ABCD-A’B’C’D’的六个面所在平面有几种位置关系?
C
B'
C'
A'
D'
B
A
D
直线与平面
直线和平面的位置关系有且只有三种
(1)直线在平面内
有无数个公共点
a
记为:a
直线与平面
(2)直线与平面相交
有且只有一个公共点
a
记为:a =A
A
直线与平面
(3)直线与平面平行
没有公共点
a
记为:a//
直线与平面
直线与平面相交或平行的情况统称为直线在平面外
记为:a
a
a//
a
a =A
A
或
直线与平面
例1. 下列命题中正确的个数是 ( )
1)若直线 l 上有无数个点不在平面 内,则 l//
2) 若直线 l 与平面 平行,则 l 与平面 内的任意一条直线都平行
3)如果两条平行直线中的一条与一个平面平行,那么另一条也与这个平面平行
4)若直线 l与平面 平行,则 l与平面 内的任意一条直线都没有公共点.
(A) 0 (B) 1 (C) 2 (D) 3
B
主要内容
直线与平面的位置关系
直线在平面内
直线与平面相交
直线与平面平行
作业
P49 练习
P51-53 习题2.1A组 4(4)(5) B 2,3
平面与平面之间的位置关系
2.1.4
平面与平面之间的位置关系
思考
(1)拿出两本书,看作两个平面,上下、左右移动和翻转,它们之间的位置关系有几种?
(2)如图,围成长方体ABCD-A′B′C′D′的六个面,两两之间的位置关系有几种?
C
B'
C'
A'
D'
B
A
D
两个平面的位置关系
两个平面的位置关系有且只有两种
①两个平面平行——没有公共点
②两个平面相交——有一条公共直线.
分类的依据是什么?
公理3 如果两个不重合的平面有一个公共点,那么它们有且只有一条过该点的公共直线.
两个平面平行或相交的画法及表示
//
m
=m
已知平面 ,直线a、b,且 // ,a ,b ,则直线a与直线b具有怎样的位置关系?
探究1
a
b
答:平行或异面
探究2
α
β
γ
a
b
l
b
α
β
γ
a
l
相交于一条交线
三条交线
三条交线
如果三个平面两两相交,那么它们的交线有多少条?画出图形表示你的结论.
一个平面可以把空间分成几个部分?
两个平面可以把空间分成几个部分?
三个平面可以把空间分成几个部分?
探究3
小结
平面与平面的位置关系
平面与平面相交
平面与平面平行
作业
P50 练习
P52 习题2.1 A组7,8
