3.1直线的倾斜角与斜率(新课标A版)
文档属性
| 名称 | 3.1直线的倾斜角与斜率(新课标A版) |

|
|
| 格式 | zip | ||
| 文件大小 | 214.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-03-29 00:00:00 | ||
图片预览






文档简介
(共36张PPT)
3.1
直线的倾斜角和斜率
主要内容
3.1.2 两条直线平行与垂直的判定
3.1.1 倾斜角与斜率
3.1.1
倾斜角与斜率
倾斜角与斜率
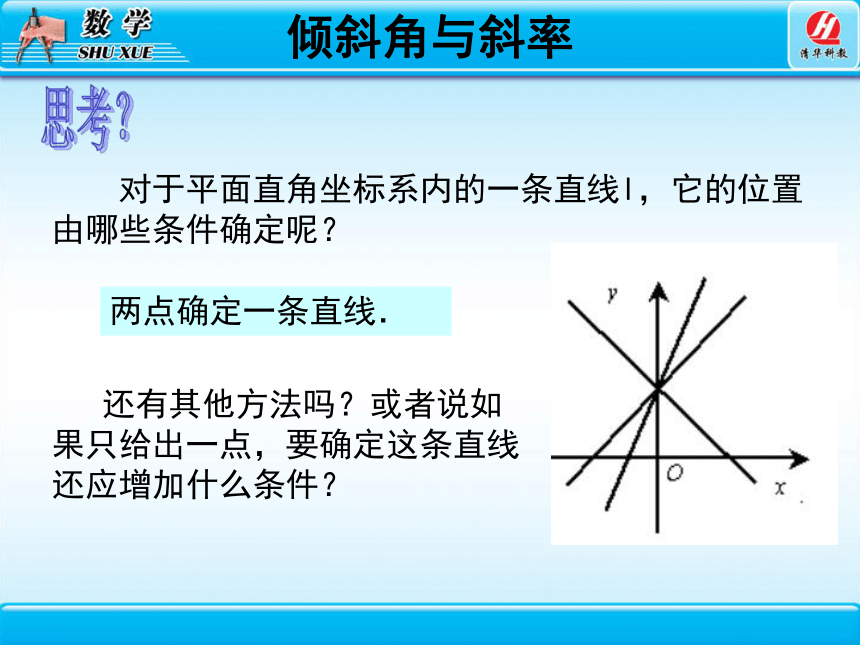
对于平面直角坐标系内的一条直线l,它的位置由哪些条件确定呢?
两点确定一条直线.
还有其他方法吗?或者说如果只给出一点,要确定这条直线还应增加什么条件?
x
y
o
P
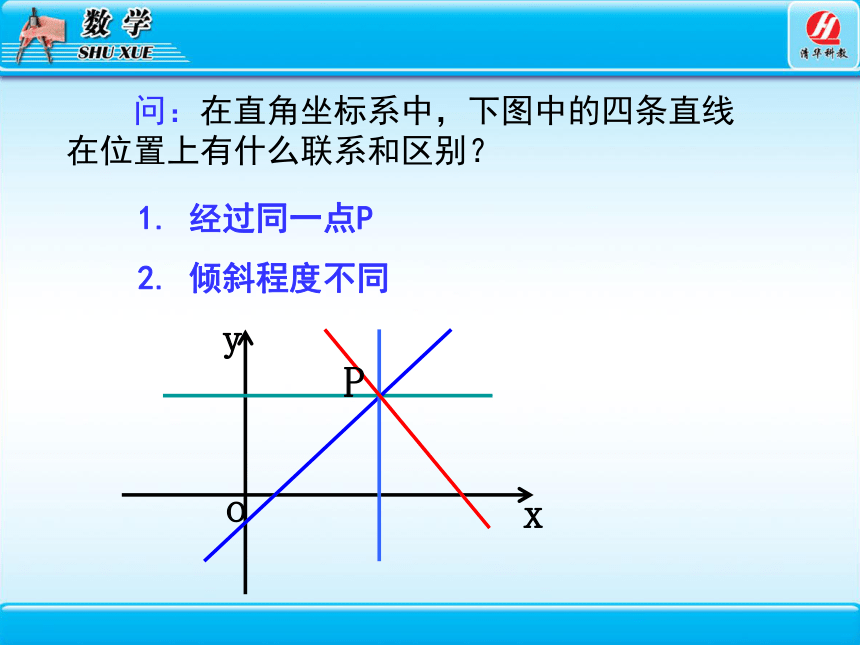
问:在直角坐标系中,下图中的四条直线在位置上有什么联系和区别?
1. 经过同一点P
2. 倾斜程度不同
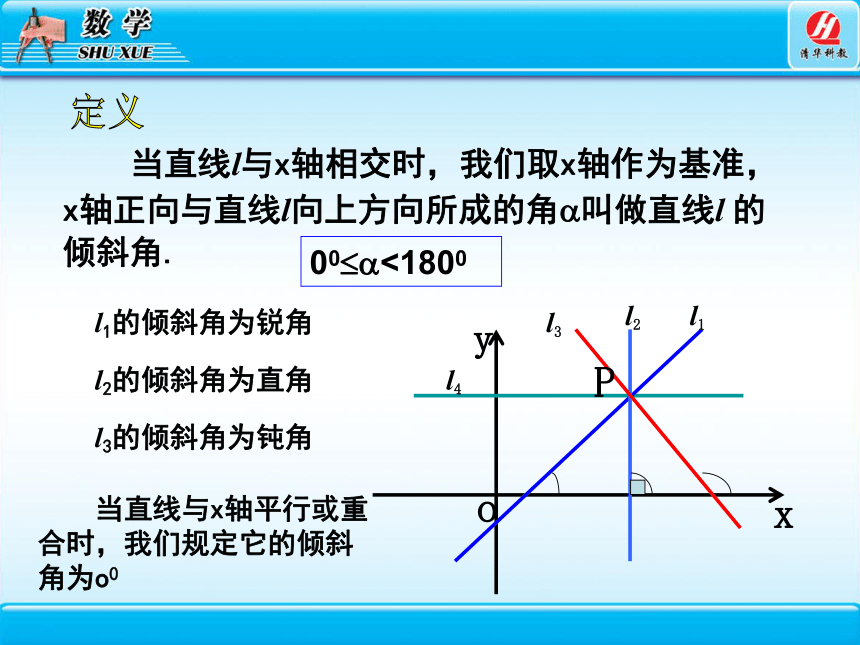
当直线l与x轴相交时,我们取x轴作为基准,x轴正向与直线l向上方向所成的角 叫做直线l 的倾斜角.
x
y
o
P
l1
l2
l3
l4
l1的倾斜角为锐角
l2的倾斜角为直角
l3的倾斜角为钝角
当直线与x轴平行或重合时,我们规定它的倾斜角为o0
00 <1800
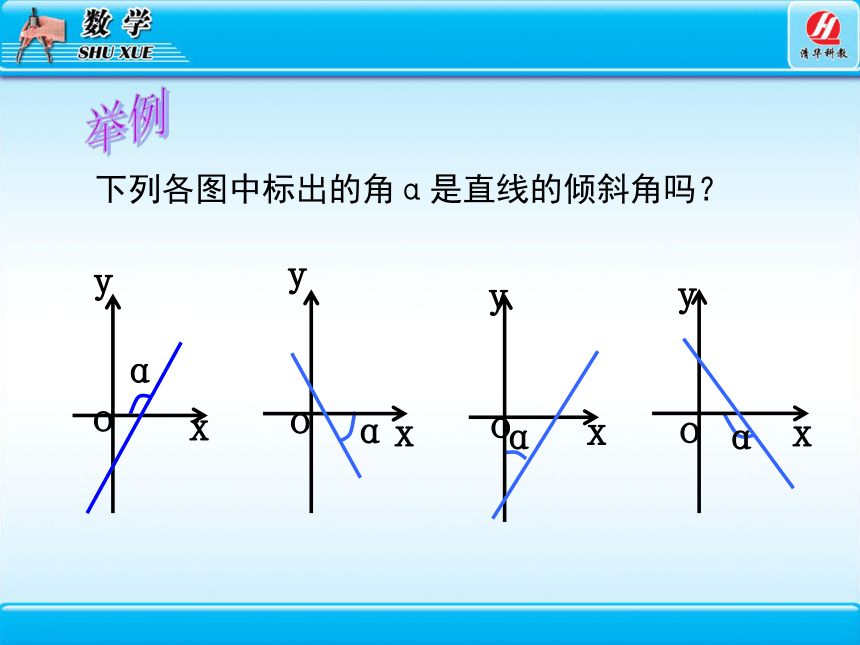
下列各图中标出的角α是直线的倾斜角吗?
x
o
y
α
x
o
y
α
x
o
y
α
x
o
y
α
平面直角坐标系内,任何一条直线都有倾斜角,倾斜角表示平面坐标系内一条直线的倾斜程度.
问:不同的直线其倾斜角一定不相同吗?
在平面直角坐标系中,已知直线上一点不能确定一条直线的位置. 同样已知直线的倾斜角,也不能确定一条直线的位置.
已知直线上一点和其倾斜角可以惟一确定一条直线.
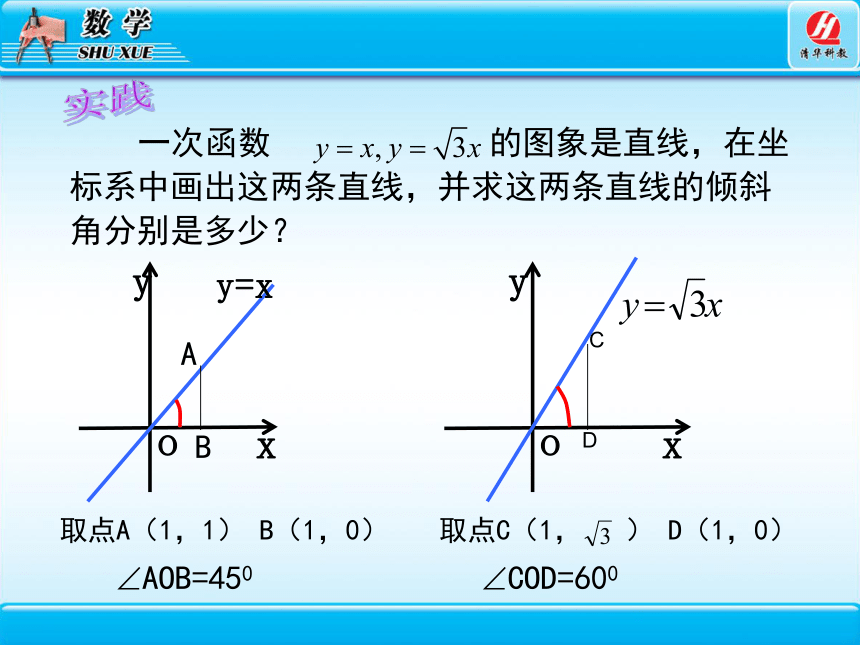
一次函数 的图象是直线,在坐标系中画出这两条直线,并求这两条直线的倾斜角分别是多少?
x
y
o
y=x
x
y
o
C
D
A
B
取点A(1,1) B(1,0)
取点C(1, ) D(1,0)
AOB=450
COD=600
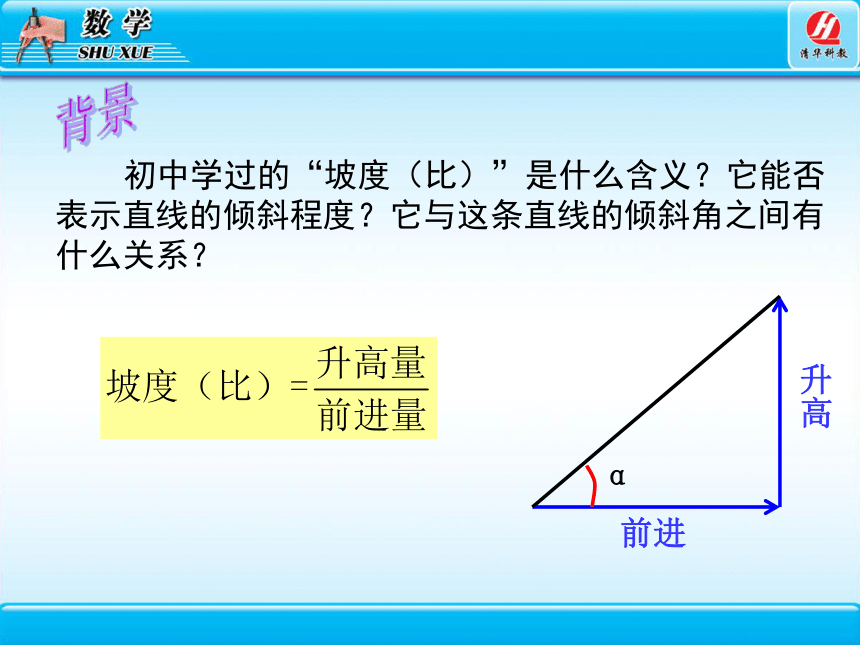
初中学过的“坡度(比)”是什么含义?它能否表示直线的倾斜程度?它与这条直线的倾斜角之间有什么关系?
前进
升高
α
我们把一条直线的倾斜角α的正切值叫做这条直线的斜率.常用小写字母k表示,即k=tanα.
任何一条直线都有斜率吗?
倾斜角是900的直线(垂直于x轴的直线)没有斜率.
1.当倾斜角α=00,300,450,600时,这条直线的斜率分别等于多少?
2.当倾斜角α=1200,1350,1500时,这条直线的斜率分别等于多少?
倾斜角为锐角时,k>0;
倾斜角为钝角时,k<0;
倾斜角为00时,k=0.
3.当直线的倾斜角在什么范围时,其斜率k>0
当直线的倾斜角在什么范围时,其斜率k<0
练习
1.指出下列直线的倾斜角和斜率:
(1)
(2)
(3)
2 .结合图形,观察倾斜角变化时,斜率的变化情况.
的定义 =tanα求出直线的斜率;
如果给定直线的倾斜角,我们当然可以根据斜率
如果给定直线上两点坐标,直线是确定的,倾斜
角也是确定的,斜率就是确定的,那么又怎么求出直
线的斜率呢?
斜率公式
x
y
o
α
P1
P2
Q
α
x
y
o
α
P1
P2
Q
已知两点P1(x1,y1)、P2(x2,y2)(其中x1≠x2),
求直线P1P2的斜率.
1.当直线P1P2平行于x轴或与x轴重合时,用上述公式求斜率.
2.当直线P1P2平行于y轴或与y轴重合时,上述公式还适用吗?为什么?
由y1=y2,得 k=0
由x1=x2,分母为零,斜率k不存在
例1 . 已知点A(3,2),B(-4,1),C(0,-l),求直线AB,BC,CA的斜率,并判断这些直线的倾斜角是锐角还是钝角.
例2 在平面直角坐标系中,画出经过原点且斜率分别为1,-1,2及-3的直线l1,l2,l3及l4.
x
y
o
l1
l2
l3
l4
思考:斜率随倾斜角逐渐变大是怎样的变化?
小结
1 直线倾斜角的概念
2 直线的倾斜角与斜率的对应关系
3 已知两点坐标,如何求直线的斜率?
斜率公式中脚标1和2有顺序吗?
P86练习:1,2,3,4.
P89习题3.1A组:1,2,3,4,5
作业
3.1.2
两条直线的平行与垂直的判定
在平面直角坐标系下,倾斜角可以表示直线的倾斜程度, 斜率也可以表示直线相对于x轴的倾斜程度。我们能否通过直线斜率来判断两条直线的位置关系
O
y
x
l1
l2
α
O
y
x
l1
l2
α1
α2
设两条直线l1,l2的斜率分别为k1,k2
若l1// l2, 则k1,k2满足什么关系?
k=tan
两条直线平行的条件
反之, 若k1=k2, ,则易得 l1// l2
对于两条不重合的直线,平行的充要条件
例1 已知A、B、C、D四点的坐标,试判断直线AB与CD的位置关系.
(1)A(2,3), B(-4,0),
C(-3,l), D(-l,2);
(2)A(-6,0),B(3,6),
C(0,3), D(6,-6)
例2.已知四边形ABCD的四个顶点分别为A(0,0), B(2,-1),C(4,2),D(2,3),试判断四边形ABCD的形状,并给出证明.
x
o
y
A
B
D
C
两条直线的垂直判定
如果两直线垂直,这两条直线的倾斜角有什么关系?斜率呢?
如图,设直线l1与l2的倾斜角分别为α1与α2,且α1<α2,
y
l1
O
x
l2
α1
α2
因为l1⊥l2 ,所以α2=900+α1
当k1·k2 =-1时,直线l1与l2一定垂直吗?
是
对于直线l1和l2,其斜率分别为k1,k2,根据上述分析可得什么结论?
y
l1
O
x
l2
α1
α2
两条直线的垂直判定
特殊情况
对于两条互相垂直的直线l1和l2,若一条直线的斜率不存在,那么另一条直线的斜率如何?
y
l1
O
x
l2
例3. 已知A(-6,0),B(3,6),P(0,3)
Q(6,-6),试判断直线AB与PQ的位置关系.
例4 已知A(5,-1),B(1,1),C(2,3),试判断△ABC的形状.
x
o
y
A
B
C
例5 已知点A(m,1),B(-3,4),C(1,m),D(-1,m+1),分别在下列条件下求实数m的值:
(1)直线AB与CD平行;
(2)直线AB与CD垂直.
小结
1.两条直线平行的判定
2.两条直线垂直的判定
3. 思想方法
倾斜角、平行是几何概念, 坐标、斜率是代数概念,解析几何的本质是用代数方法来研究几何问题.
作业
P89练习:1,2.
P90习题3.1 A组:8. B组:3,4.
3.1
直线的倾斜角和斜率
主要内容
3.1.2 两条直线平行与垂直的判定
3.1.1 倾斜角与斜率
3.1.1
倾斜角与斜率
倾斜角与斜率
对于平面直角坐标系内的一条直线l,它的位置由哪些条件确定呢?
两点确定一条直线.
还有其他方法吗?或者说如果只给出一点,要确定这条直线还应增加什么条件?
x
y
o
P
问:在直角坐标系中,下图中的四条直线在位置上有什么联系和区别?
1. 经过同一点P
2. 倾斜程度不同
当直线l与x轴相交时,我们取x轴作为基准,x轴正向与直线l向上方向所成的角 叫做直线l 的倾斜角.
x
y
o
P
l1
l2
l3
l4
l1的倾斜角为锐角
l2的倾斜角为直角
l3的倾斜角为钝角
当直线与x轴平行或重合时,我们规定它的倾斜角为o0
00 <1800
下列各图中标出的角α是直线的倾斜角吗?
x
o
y
α
x
o
y
α
x
o
y
α
x
o
y
α
平面直角坐标系内,任何一条直线都有倾斜角,倾斜角表示平面坐标系内一条直线的倾斜程度.
问:不同的直线其倾斜角一定不相同吗?
在平面直角坐标系中,已知直线上一点不能确定一条直线的位置. 同样已知直线的倾斜角,也不能确定一条直线的位置.
已知直线上一点和其倾斜角可以惟一确定一条直线.
一次函数 的图象是直线,在坐标系中画出这两条直线,并求这两条直线的倾斜角分别是多少?
x
y
o
y=x
x
y
o
C
D
A
B
取点A(1,1) B(1,0)
取点C(1, ) D(1,0)
AOB=450
COD=600
初中学过的“坡度(比)”是什么含义?它能否表示直线的倾斜程度?它与这条直线的倾斜角之间有什么关系?
前进
升高
α
我们把一条直线的倾斜角α的正切值叫做这条直线的斜率.常用小写字母k表示,即k=tanα.
任何一条直线都有斜率吗?
倾斜角是900的直线(垂直于x轴的直线)没有斜率.
1.当倾斜角α=00,300,450,600时,这条直线的斜率分别等于多少?
2.当倾斜角α=1200,1350,1500时,这条直线的斜率分别等于多少?
倾斜角为锐角时,k>0;
倾斜角为钝角时,k<0;
倾斜角为00时,k=0.
3.当直线的倾斜角在什么范围时,其斜率k>0
当直线的倾斜角在什么范围时,其斜率k<0
练习
1.指出下列直线的倾斜角和斜率:
(1)
(2)
(3)
2 .结合图形,观察倾斜角变化时,斜率的变化情况.
的定义 =tanα求出直线的斜率;
如果给定直线的倾斜角,我们当然可以根据斜率
如果给定直线上两点坐标,直线是确定的,倾斜
角也是确定的,斜率就是确定的,那么又怎么求出直
线的斜率呢?
斜率公式
x
y
o
α
P1
P2
Q
α
x
y
o
α
P1
P2
Q
已知两点P1(x1,y1)、P2(x2,y2)(其中x1≠x2),
求直线P1P2的斜率.
1.当直线P1P2平行于x轴或与x轴重合时,用上述公式求斜率.
2.当直线P1P2平行于y轴或与y轴重合时,上述公式还适用吗?为什么?
由y1=y2,得 k=0
由x1=x2,分母为零,斜率k不存在
例1 . 已知点A(3,2),B(-4,1),C(0,-l),求直线AB,BC,CA的斜率,并判断这些直线的倾斜角是锐角还是钝角.
例2 在平面直角坐标系中,画出经过原点且斜率分别为1,-1,2及-3的直线l1,l2,l3及l4.
x
y
o
l1
l2
l3
l4
思考:斜率随倾斜角逐渐变大是怎样的变化?
小结
1 直线倾斜角的概念
2 直线的倾斜角与斜率的对应关系
3 已知两点坐标,如何求直线的斜率?
斜率公式中脚标1和2有顺序吗?
P86练习:1,2,3,4.
P89习题3.1A组:1,2,3,4,5
作业
3.1.2
两条直线的平行与垂直的判定
在平面直角坐标系下,倾斜角可以表示直线的倾斜程度, 斜率也可以表示直线相对于x轴的倾斜程度。我们能否通过直线斜率来判断两条直线的位置关系
O
y
x
l1
l2
α
O
y
x
l1
l2
α1
α2
设两条直线l1,l2的斜率分别为k1,k2
若l1// l2, 则k1,k2满足什么关系?
k=tan
两条直线平行的条件
反之, 若k1=k2, ,则易得 l1// l2
对于两条不重合的直线,平行的充要条件
例1 已知A、B、C、D四点的坐标,试判断直线AB与CD的位置关系.
(1)A(2,3), B(-4,0),
C(-3,l), D(-l,2);
(2)A(-6,0),B(3,6),
C(0,3), D(6,-6)
例2.已知四边形ABCD的四个顶点分别为A(0,0), B(2,-1),C(4,2),D(2,3),试判断四边形ABCD的形状,并给出证明.
x
o
y
A
B
D
C
两条直线的垂直判定
如果两直线垂直,这两条直线的倾斜角有什么关系?斜率呢?
如图,设直线l1与l2的倾斜角分别为α1与α2,且α1<α2,
y
l1
O
x
l2
α1
α2
因为l1⊥l2 ,所以α2=900+α1
当k1·k2 =-1时,直线l1与l2一定垂直吗?
是
对于直线l1和l2,其斜率分别为k1,k2,根据上述分析可得什么结论?
y
l1
O
x
l2
α1
α2
两条直线的垂直判定
特殊情况
对于两条互相垂直的直线l1和l2,若一条直线的斜率不存在,那么另一条直线的斜率如何?
y
l1
O
x
l2
例3. 已知A(-6,0),B(3,6),P(0,3)
Q(6,-6),试判断直线AB与PQ的位置关系.
例4 已知A(5,-1),B(1,1),C(2,3),试判断△ABC的形状.
x
o
y
A
B
C
例5 已知点A(m,1),B(-3,4),C(1,m),D(-1,m+1),分别在下列条件下求实数m的值:
(1)直线AB与CD平行;
(2)直线AB与CD垂直.
小结
1.两条直线平行的判定
2.两条直线垂直的判定
3. 思想方法
倾斜角、平行是几何概念, 坐标、斜率是代数概念,解析几何的本质是用代数方法来研究几何问题.
作业
P89练习:1,2.
P90习题3.1 A组:8. B组:3,4.
