3.2直线的方程
图片预览










文档简介
(共39张PPT)
直线的方程
3.2
主要内容
3.2.2 直线的两点式方程
3.2.3 直线的一般式方程
3.2.1 直线的点斜式方程
直线的点斜式方程
3.2.1
在平面直角坐标系内,如果给定一条直线 经过的一个点 和斜率 ,能否将直线上所有的点的坐标 满足的关系表示出来呢?
x
y
O
l
即:
x
y
O
l
点斜式方程
点斜式方程
直线 经过点 ,且斜率为 ,设点 是直线上不同于点 的任意一点,因为直线 的斜率为 ,由斜率公式得:
P
(1)过点 ,斜率是 的直线 上的点,其坐标都满足方程 吗?
(2)坐标满足方程 的点都在过点 斜率为 的直线 上吗?
上述两条都成立,所以这个方程
就是过点 斜率为 的直线 的方程.
点斜式方程
,或
x
y
O
l
的方程就是
(1) 轴所在直线的方程是什么?
当直线 的倾斜角为 时,即 .
这时直线 与 轴平行或重合,
(2) 轴所在直线的方程是什么?
,或
当直线 的倾斜角为 时,直线没有斜率,这时,直线 与 轴平行或重合,它的方程不能用点斜式表示.这时,直线 上每一点的横坐标都等于 ,所以它的方程就是
x
y
O
l
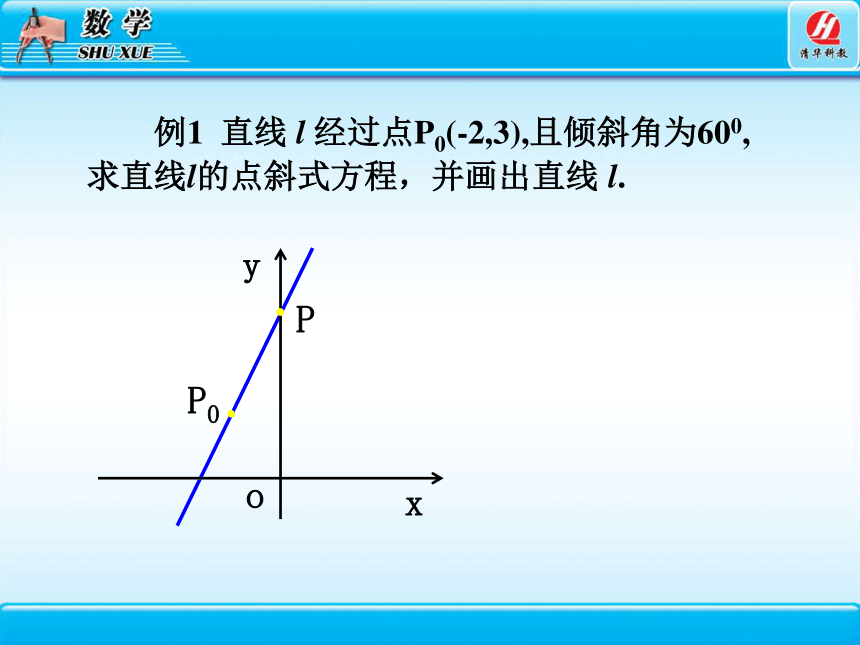
例1 直线 l 经过点P0(-2,3),且倾斜角为600,求直线l的点斜式方程,并画出直线 l.
P0
P
x
y
o
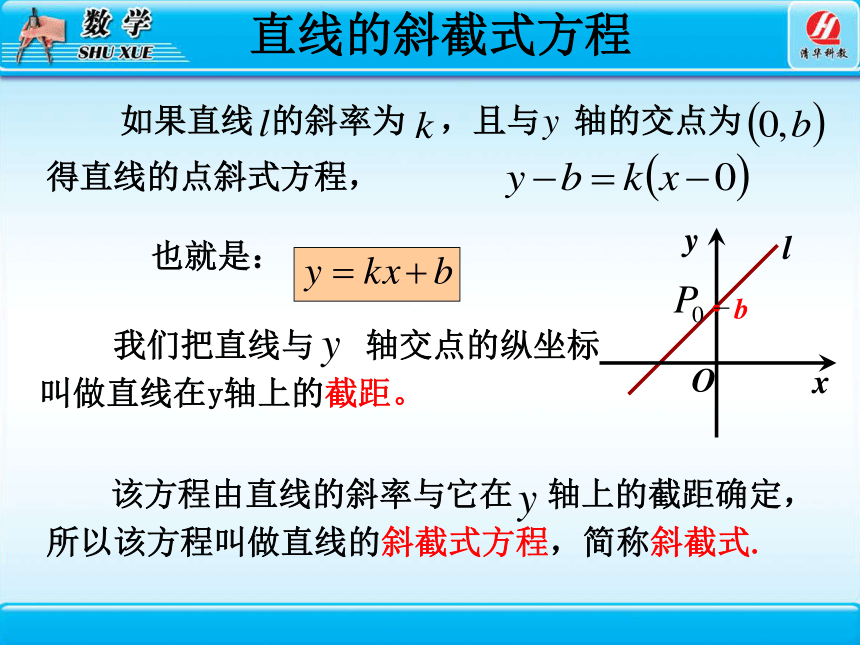
如果直线 的斜率为 ,且与 轴的交点为
得直线的点斜式方程,
也就是:
x
y
O
l
b
我们把直线与 轴交点的纵坐标叫做直线在y轴上的截距。
该方程由直线的斜率与它在 轴上的截距确定,所以该方程叫做直线的斜截式方程,简称斜截式.
直线的斜截式方程
例2 已知直线 , 试讨论:(1) 的条件是什么?(2) 的条件是什么?
解:
,且 ;
例3 求下列直线的斜截式方程:
(1)经过点A(-1,2),且与直线 y=3x+1垂直;
(2)斜率为-2,且在x轴上的截距为5.
例4 已知直线 l 的斜率为 ,且与两坐标轴围成的三角形的面积为4,求直线l的方程.
1. 直线的点斜式方程:
2. 直线的斜截式方程:
小结
①直线和x轴平行时,倾斜角α=0°
②直线与x轴垂直时,倾斜角α=90°
3. 特殊情况
作业
P95练习:1,2,3,4
P100习题3.2 A组:1,5,6,10.
3.2.2
直线的两点式方程
已知直线经过两点P1(x1,y1),P2(x2,y2),(x1 x2 ,y1 y2),如何求出这两个点的直线方程呢?
经过一点,且已知斜率的直线,可以写出它的点斜式方程.
可以先求出斜率,再选择一点,得到点斜式方程.
两点式方程
x
y
l
P2(x2,y2)
两点式
P1(x1,y1)
斜率
根据两点P1(x1,y1),P2(x2,y2),
截距式方程
x
y
l
A(a,0)
截距式
B(0,b)
解:代入两点式方程得
化简得
横截距
纵截距
例1. 已知直线经过点A(a,0),B(0,b),a 0,b 0,求直线方程
中点坐标公式
已知两点P1(x1,y1),P2(x2,y2)则线段P1P2的中点P0的坐标是什么?
x
y
A(x1,y1)
B(x2,y2)
中点
P0的坐标为
例2 已知三角形的三个顶点 A(-5,0),B(3,-3),C(0,2),求BC边所在直线的方程,以及该边上中线所在直线的方程.
A
B
x
y
o
C
M
例3.求经过点P(-5,4),且在两坐标轴上的截距相等的直线方程.
P
x
y
o
例4 求经过点P(0,3),且在两坐标轴上的截距之和为2的直线方程.
例5. 已知直线 l 经过点P(1,2),并且点A(2,3)和点 B(4,-5)到直线l 的距离相等,求直线l 的方程.
P
x
y
o
B
A
直线方程小结
两点坐标
两点式
点斜式
两个截距
截距式
P97练习:1,2.
P100习题3.2A组:3,4,8,9,11.
作业
3.2.3
直线的一般式方程
1. 平面直角坐标系中的每一条直线都可以用一个关于x,y的二元一次方程表示吗?
2. 每一个关于x,y的二元一次方程都表示一条直线吗?
讨论
1. 直线的点斜式、斜截式、两点式、截距式都是关于X,y的二元一次方程
2. 经过点P(x0,y0)且斜率不存在的直线的方程:
x-x0=0
可以看成y的系数为0的二元一次方程.
对于二元一次方程 Ax+By+C=0(A,B不全为零)
1)当B 0时可化为
表示经过点(0, ),斜率k为 的直线.
2) 当B=0时,A 0,方程可化为
表示垂直于x轴的直线.
直线的一般式方程
(其中A,B不同时为0)
1. 所有的直线都可以用二元一次方程表示
2. 所有二元一次方程都表示直线
此方程叫做直线的一般式方程
例1 已知直线经过点A(6,-4),斜率为 ,求直线的点斜式和一般式方程.
例2 把直线l 的一般式方程 x-2y+6=0化成斜截式,求出直线l 的斜率以及它在x轴与y轴上的截距,并画出图形.
两条直线平行和垂直的条件
平行
垂直
重合
例3 已知直线
l1:ax+(a+1)y-a=0
和 l2:(a+2)x+2(a+1)y-4=0,
若l1//l2,求a的值.
例4 已知直线l1:x-ay-1=0和l2:a2x+y+2=0,
若l1⊥l2,求a的值.
小结
点斜式
斜率和一点坐标
斜截式
斜率k和截距b
两点坐标
两点式
点斜式
两个截距
截距式
一般式
小结
1.直线的点斜式、斜截式、两点式、截距式都可以化成一般式. 反之不一定.
2. 特殊的直线方程 如x+2=0, 2y-3=0.
有时不存在点斜式或斜截式、两点式、截距式.
3. 根据一般方程也能很快判断两条直线的位置关系.
4. 一般不特别指明时直线方程的结果都要化成一般式.
P99-100练习:1,2.
P101习题3.2B组:1,2,5.
作业
直线的方程
3.2
主要内容
3.2.2 直线的两点式方程
3.2.3 直线的一般式方程
3.2.1 直线的点斜式方程
直线的点斜式方程
3.2.1
在平面直角坐标系内,如果给定一条直线 经过的一个点 和斜率 ,能否将直线上所有的点的坐标 满足的关系表示出来呢?
x
y
O
l
即:
x
y
O
l
点斜式方程
点斜式方程
直线 经过点 ,且斜率为 ,设点 是直线上不同于点 的任意一点,因为直线 的斜率为 ,由斜率公式得:
P
(1)过点 ,斜率是 的直线 上的点,其坐标都满足方程 吗?
(2)坐标满足方程 的点都在过点 斜率为 的直线 上吗?
上述两条都成立,所以这个方程
就是过点 斜率为 的直线 的方程.
点斜式方程
,或
x
y
O
l
的方程就是
(1) 轴所在直线的方程是什么?
当直线 的倾斜角为 时,即 .
这时直线 与 轴平行或重合,
(2) 轴所在直线的方程是什么?
,或
当直线 的倾斜角为 时,直线没有斜率,这时,直线 与 轴平行或重合,它的方程不能用点斜式表示.这时,直线 上每一点的横坐标都等于 ,所以它的方程就是
x
y
O
l
例1 直线 l 经过点P0(-2,3),且倾斜角为600,求直线l的点斜式方程,并画出直线 l.
P0
P
x
y
o
如果直线 的斜率为 ,且与 轴的交点为
得直线的点斜式方程,
也就是:
x
y
O
l
b
我们把直线与 轴交点的纵坐标叫做直线在y轴上的截距。
该方程由直线的斜率与它在 轴上的截距确定,所以该方程叫做直线的斜截式方程,简称斜截式.
直线的斜截式方程
例2 已知直线 , 试讨论:(1) 的条件是什么?(2) 的条件是什么?
解:
,且 ;
例3 求下列直线的斜截式方程:
(1)经过点A(-1,2),且与直线 y=3x+1垂直;
(2)斜率为-2,且在x轴上的截距为5.
例4 已知直线 l 的斜率为 ,且与两坐标轴围成的三角形的面积为4,求直线l的方程.
1. 直线的点斜式方程:
2. 直线的斜截式方程:
小结
①直线和x轴平行时,倾斜角α=0°
②直线与x轴垂直时,倾斜角α=90°
3. 特殊情况
作业
P95练习:1,2,3,4
P100习题3.2 A组:1,5,6,10.
3.2.2
直线的两点式方程
已知直线经过两点P1(x1,y1),P2(x2,y2),(x1 x2 ,y1 y2),如何求出这两个点的直线方程呢?
经过一点,且已知斜率的直线,可以写出它的点斜式方程.
可以先求出斜率,再选择一点,得到点斜式方程.
两点式方程
x
y
l
P2(x2,y2)
两点式
P1(x1,y1)
斜率
根据两点P1(x1,y1),P2(x2,y2),
截距式方程
x
y
l
A(a,0)
截距式
B(0,b)
解:代入两点式方程得
化简得
横截距
纵截距
例1. 已知直线经过点A(a,0),B(0,b),a 0,b 0,求直线方程
中点坐标公式
已知两点P1(x1,y1),P2(x2,y2)则线段P1P2的中点P0的坐标是什么?
x
y
A(x1,y1)
B(x2,y2)
中点
P0的坐标为
例2 已知三角形的三个顶点 A(-5,0),B(3,-3),C(0,2),求BC边所在直线的方程,以及该边上中线所在直线的方程.
A
B
x
y
o
C
M
例3.求经过点P(-5,4),且在两坐标轴上的截距相等的直线方程.
P
x
y
o
例4 求经过点P(0,3),且在两坐标轴上的截距之和为2的直线方程.
例5. 已知直线 l 经过点P(1,2),并且点A(2,3)和点 B(4,-5)到直线l 的距离相等,求直线l 的方程.
P
x
y
o
B
A
直线方程小结
两点坐标
两点式
点斜式
两个截距
截距式
P97练习:1,2.
P100习题3.2A组:3,4,8,9,11.
作业
3.2.3
直线的一般式方程
1. 平面直角坐标系中的每一条直线都可以用一个关于x,y的二元一次方程表示吗?
2. 每一个关于x,y的二元一次方程都表示一条直线吗?
讨论
1. 直线的点斜式、斜截式、两点式、截距式都是关于X,y的二元一次方程
2. 经过点P(x0,y0)且斜率不存在的直线的方程:
x-x0=0
可以看成y的系数为0的二元一次方程.
对于二元一次方程 Ax+By+C=0(A,B不全为零)
1)当B 0时可化为
表示经过点(0, ),斜率k为 的直线.
2) 当B=0时,A 0,方程可化为
表示垂直于x轴的直线.
直线的一般式方程
(其中A,B不同时为0)
1. 所有的直线都可以用二元一次方程表示
2. 所有二元一次方程都表示直线
此方程叫做直线的一般式方程
例1 已知直线经过点A(6,-4),斜率为 ,求直线的点斜式和一般式方程.
例2 把直线l 的一般式方程 x-2y+6=0化成斜截式,求出直线l 的斜率以及它在x轴与y轴上的截距,并画出图形.
两条直线平行和垂直的条件
平行
垂直
重合
例3 已知直线
l1:ax+(a+1)y-a=0
和 l2:(a+2)x+2(a+1)y-4=0,
若l1//l2,求a的值.
例4 已知直线l1:x-ay-1=0和l2:a2x+y+2=0,
若l1⊥l2,求a的值.
小结
点斜式
斜率和一点坐标
斜截式
斜率k和截距b
两点坐标
两点式
点斜式
两个截距
截距式
一般式
小结
1.直线的点斜式、斜截式、两点式、截距式都可以化成一般式. 反之不一定.
2. 特殊的直线方程 如x+2=0, 2y-3=0.
有时不存在点斜式或斜截式、两点式、截距式.
3. 根据一般方程也能很快判断两条直线的位置关系.
4. 一般不特别指明时直线方程的结果都要化成一般式.
P99-100练习:1,2.
P101习题3.2B组:1,2,5.
作业
