2020-2021沪科版七年级下册 10.2平行线的判定(二)课件(共15张ppt)
文档属性
| 名称 | 2020-2021沪科版七年级下册 10.2平行线的判定(二)课件(共15张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 491.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-29 21:22:05 | ||
图片预览




文档简介
(共15张PPT)
课题导入
我们学过的两条直线平行的判定方法是什么?
同位角相等,两直线平行.
还有其它方法吗?
1.平行线的定义
2.平行线的判定1
课题导入
目标引领
1.利用平行线判定方法1结合简单推理得出平行线判定方法2和方法3.
2.会运用平行线的判定方法证明两直线平行.
独立自学
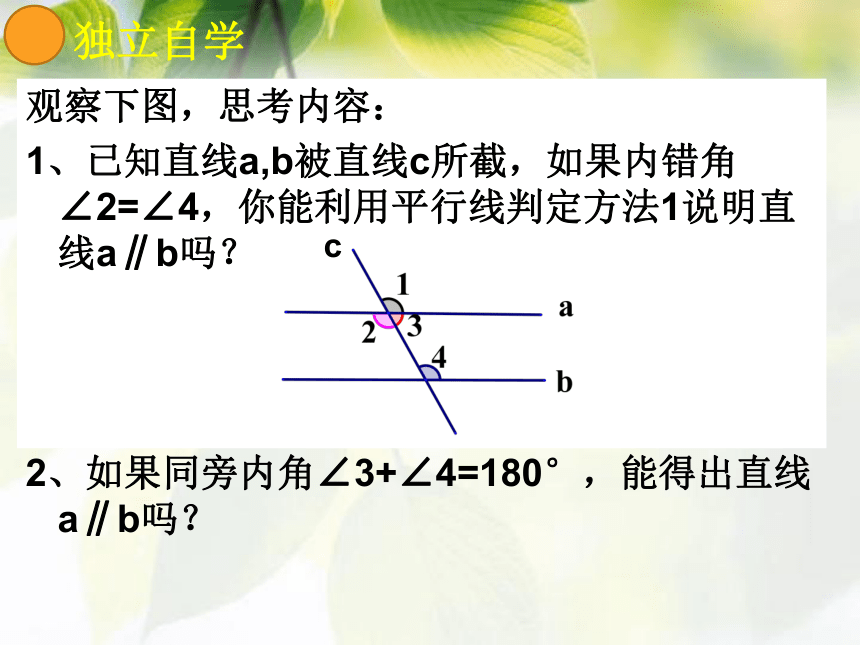
观察下图,思考内容:
1、已知直线a,b被直线c所截,如果内错角∠2=∠4,你能利用平行线判定方法1说明直线a∥b吗?
2、如果同旁内角∠3+∠4=180°,能得出直线a∥b吗?
c
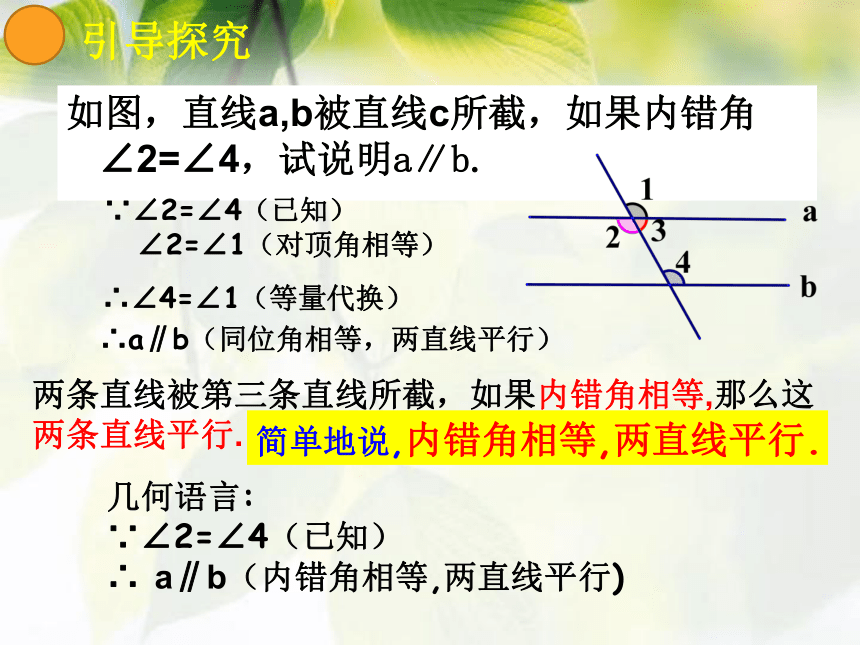
如图,直线a,b被直线c所截,如果内错角∠2=∠4,试说明a∥b.
∵∠2=∠4(已知)
∠2=∠1(对顶角相等)
∴∠4=∠1(等量代换)
∴a∥b(同位角相等,两直线平行)
两条直线被第三条直线所截,如果内错角相等,那么这两条直线平行.
引导探究
简单地说,内错角相等,两直线平行.
几何语言:
∵∠2=∠4(已知)
∴
a∥b(内错角相等,两直线平行)
如图,直线a,b被直线c所截,如果同旁内角∠3+∠4=180°,试说明a∥b.
∵
∠3+∠4=180°(已知)
∠2+∠3=180°(邻补角定义)
∴∠2=∠4(同角的补角相等)
∴
a∥b(内错角相等,两直线平行)
两条直线被第三条直线所截,如果同旁内角互补,那么这两条直线平行.
引导探究
几何语言:
∵
∠3+∠4=180
°(已知)
∴
a∥b(同旁内角互补,
两直线平行)
简单地说,同旁内角互补,两直线平行.
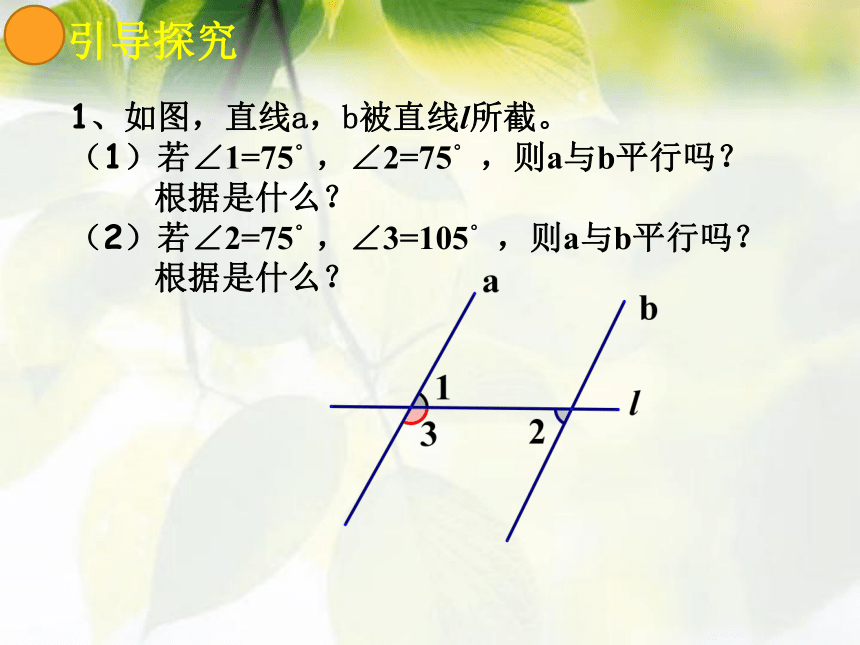
1、如图,直线a,b被直线l所截。
(1)若∠1=75°,∠2=75°
,则a与b平行吗?
根据是什么?
(2)若∠2=75°,∠3=105°
,则a与b平行吗?
根据是什么?
引导探究
2、如图,∠1=∠3,∠1=∠2,那么DE与BC有什么位置关系?为什么?
引导探究
2.如果两条直线和第三条直线平行,那么这两条直线平行。(平行线的传递性)
3.同位角相等,
两直线平行.
4.内错角相等,
两直线平行.
5.同旁内角互补,
两直线平行.
6.
在同一平面内,垂直于同一条直线的两直线平行
判定两条直线是否平行的常见方法:
引导探究
1.
平行线的定义.
3.如图,有以下四个条件:
(1)∠A+∠ABC=180°
(2)∠1=∠2
(3)∠5=∠4
(4)∠A=∠3
其中能判定AD∥BC的条件有
.
引导探究
A
B
C
D
1
2
3
4
5
变式:一辆汽车在公路上行驶,两次拐弯后,仍在原来的方向上行驶,那么两次拐弯的角度可能为(
)
A.
第一次右拐60°,第二次右拐120°
B.
第一次右拐60°,第二次右拐60°
C.
第一次右拐60°,第二次左拐120°
D.
第一次右拐60°,第二次左拐60°
引导探究
4.如图∠1=53°,∠2=127°,∠3=53°,试说明直线AB与CD,BC与DE的位置关系.
2
4
3
1
引导探究
5.如图,GH分别交AB、CD于点E、F,∠AEF=∠EFD.
(1)试写出AB∥CD的依据;
(2)若EM是∠AEF的平分线,FN是
∠EFD的平分线,则EM、FN平行吗?
若平行,请说明理由.
目标升华
谈谈这节课你有哪些收获或疑惑?
1、如图1,已知AC平分∠DAB,∠1=∠2,由AC平分∠DAB,得∠1=
,又因为∠1=∠2,所以∠2=
,所以AB∥
.
D
1
2
3
A
B
C
当堂诊学
2.如图2,∠1=65°,
∠2=65°,
∠3=115°,试说明DE∥BC,DF∥AB.
F
1
2
3
4
A
B
C
D
E
图1
图2
∠3
∠3
CD
强化补清
1、P127练习1、2、3.
2、同步练习.
课题导入
我们学过的两条直线平行的判定方法是什么?
同位角相等,两直线平行.
还有其它方法吗?
1.平行线的定义
2.平行线的判定1
课题导入
目标引领
1.利用平行线判定方法1结合简单推理得出平行线判定方法2和方法3.
2.会运用平行线的判定方法证明两直线平行.
独立自学
观察下图,思考内容:
1、已知直线a,b被直线c所截,如果内错角∠2=∠4,你能利用平行线判定方法1说明直线a∥b吗?
2、如果同旁内角∠3+∠4=180°,能得出直线a∥b吗?
c
如图,直线a,b被直线c所截,如果内错角∠2=∠4,试说明a∥b.
∵∠2=∠4(已知)
∠2=∠1(对顶角相等)
∴∠4=∠1(等量代换)
∴a∥b(同位角相等,两直线平行)
两条直线被第三条直线所截,如果内错角相等,那么这两条直线平行.
引导探究
简单地说,内错角相等,两直线平行.
几何语言:
∵∠2=∠4(已知)
∴
a∥b(内错角相等,两直线平行)
如图,直线a,b被直线c所截,如果同旁内角∠3+∠4=180°,试说明a∥b.
∵
∠3+∠4=180°(已知)
∠2+∠3=180°(邻补角定义)
∴∠2=∠4(同角的补角相等)
∴
a∥b(内错角相等,两直线平行)
两条直线被第三条直线所截,如果同旁内角互补,那么这两条直线平行.
引导探究
几何语言:
∵
∠3+∠4=180
°(已知)
∴
a∥b(同旁内角互补,
两直线平行)
简单地说,同旁内角互补,两直线平行.
1、如图,直线a,b被直线l所截。
(1)若∠1=75°,∠2=75°
,则a与b平行吗?
根据是什么?
(2)若∠2=75°,∠3=105°
,则a与b平行吗?
根据是什么?
引导探究
2、如图,∠1=∠3,∠1=∠2,那么DE与BC有什么位置关系?为什么?
引导探究
2.如果两条直线和第三条直线平行,那么这两条直线平行。(平行线的传递性)
3.同位角相等,
两直线平行.
4.内错角相等,
两直线平行.
5.同旁内角互补,
两直线平行.
6.
在同一平面内,垂直于同一条直线的两直线平行
判定两条直线是否平行的常见方法:
引导探究
1.
平行线的定义.
3.如图,有以下四个条件:
(1)∠A+∠ABC=180°
(2)∠1=∠2
(3)∠5=∠4
(4)∠A=∠3
其中能判定AD∥BC的条件有
.
引导探究
A
B
C
D
1
2
3
4
5
变式:一辆汽车在公路上行驶,两次拐弯后,仍在原来的方向上行驶,那么两次拐弯的角度可能为(
)
A.
第一次右拐60°,第二次右拐120°
B.
第一次右拐60°,第二次右拐60°
C.
第一次右拐60°,第二次左拐120°
D.
第一次右拐60°,第二次左拐60°
引导探究
4.如图∠1=53°,∠2=127°,∠3=53°,试说明直线AB与CD,BC与DE的位置关系.
2
4
3
1
引导探究
5.如图,GH分别交AB、CD于点E、F,∠AEF=∠EFD.
(1)试写出AB∥CD的依据;
(2)若EM是∠AEF的平分线,FN是
∠EFD的平分线,则EM、FN平行吗?
若平行,请说明理由.
目标升华
谈谈这节课你有哪些收获或疑惑?
1、如图1,已知AC平分∠DAB,∠1=∠2,由AC平分∠DAB,得∠1=
,又因为∠1=∠2,所以∠2=
,所以AB∥
.
D
1
2
3
A
B
C
当堂诊学
2.如图2,∠1=65°,
∠2=65°,
∠3=115°,试说明DE∥BC,DF∥AB.
F
1
2
3
4
A
B
C
D
E
图1
图2
∠3
∠3
CD
强化补清
1、P127练习1、2、3.
2、同步练习.
