2012年中考数学考前指导(精品)
图片预览




文档简介
2012年中考数学考前指导
江苏省南通市港口中学 初三数学备课组 2012-3-28
考前指导是初中数学教学的最后一个环节.
经过3年的学习和紧张的几个月的复习准备后,同学们将要走进考场,实现自己的宏愿.但是能否将自己的实际水平如实地在考卷上全面正确地反映出来,除了要有扎实的知识功底外,还要掌握一些应考的策略技巧和必要的心理调适,注意应试技巧,尽量减少失误,考出最好成绩.
一、常见的心理障碍及其防治
有的同学临考时心情紧张,唯恐考不好,于是一些不良反应随之而来:如失眠、健忘、运算失误等,拿到卷子甚至头脑里一片空白,产生这种心理障碍的原因是对中考的功能及技巧策略不甚了解,中考除了对掌握的基础知识和技能进行测试外,同时也是一次心理素质和身体素质的测试.因此,心理上要有充分的准备,防治的方法主要有:
1、考前要有充分的时间休息,充分放松,出外散步,不开夜车,不做难题,不争辩等;
2、考场放松法是一种心理放松法,放松的原理是用紧张克服紧张,即用超觉静思法,使全身放松,平静心情,这样血液中含氧量充足,你必然会头脑清晰,自然就能超水平发挥.
3、必胜信心——精神胜利法,肯定的暗示会使自己发挥得更好.自己对自己说,我的能力超过试卷要求,我一定会考得很好,你也可以采取其它的肯定暗示语,这样自我表扬后,您的大脑为您的考试卖力工作,必然会取得理想成绩.
4、考前给自己看“病”,每一位考生在学习过程中都会存在这样或那样的“毛病”,这并不奇怪.但是在考前要努力把这些“毛病”治好.为此,你必须把自己做过的试题、试卷、笔记、错题集等重新看一遍,查一查那些没得分或被扣分的问题是怎么做的,做错的原因是什么,如果是因为知识没掌握,就要把这部分知识弄懂;如果是因为“粗心”,就要努力改变自己的不良习惯;如果是因为不会用正确的思想方法去分析问题、解决问题,那更要向老师、同学请教,并学习思考的方法,悟出道理;如果有别的同学请你“看病”,你更要认真地去“望闻问切”,以检验自己是否真会,增加一些“临床”经验.防止自己犯同样的“病”,考前给自己看病、治病,不带任何问题、任何疑点进考场,一定能收到意想不到的效果.
二、临场发挥策略技巧
搞好临场发挥是顺利通过中考最后一关的关键,这好比农民种田的收割季节,虽然农作物的长势很好,但如不能做到颗粒归仓,仍然得不到高产量.实际中,确有一些考生丢掉了本可以稳得的分数,非常令人遗憾.如何搞好临场发挥、提高应试技巧呢?
1、浏览全卷,把握全貌,科学分配答题时间.
⑴充分利用好考前5分钟,通读全卷,了解共有几页、正反面是否都有题目,如不全有,应及时反映给监考老师换卷子.试题类型、难易程度、每题的分值,对完成整卷自己所需的时间作一估计,如果估计比较乐观,答题时更要谨慎,因为有些题目看上去很简单,其实有命题人设置的陷阱等,如“零陷阱”,需要分类讨论,几何中的多解陷阱等;如果估计不乐观,那更要沉着对待,因为短时一瞥不是深思熟虑的结果,如果因此失去信心,就等于给自己设置障碍,减少成功机会.
⑵科学分配答卷时间的基本原则是保证在能得分的地方绝不失分,不易得分的地方争取得分,心目中要有分数时间比,如一道题目准备用3分钟,但3分钟过后一点眉目都没有,你可先跳开,但若已接近成功,延长一点时间也是必要的,分配时间,应保证考试成功的目的.
2、答题技巧:将试题分三批来做,力争一次性正确.
第一批是有把握做对的试题,这类题属“确保”范围,必须集中精力加以攻克,力争不失分,为保底的120—125分打下坚实的基础.
第二批是做心中有数但并非十分有把握的题目,这是“力争”范围,必须花力气突破,这样就可实现总分140分的目标,你有可能进入全县的前800名行列之中了.
第三批是做少数不太熟悉的题目,这时由于胜利在握,心情轻松愉快,思维畅通无阻,本来不会做的题目,你一定有可能做起来,有可能冲击满分,即使个别小题不会做,也要写上几步,多少也能拿点分,也不会影响考试全局,无非是帮其它科目少带了几分而己.
3、临场超水平发挥,必须遵循的原则
⑴先易后难,先简后繁,从前向后,步步为营,稳扎稳打,忌钻牛角尖和心算,循序渐进,这样有利于在考试中知识与技能的再现.
考试开始,因紧张手脑没有活动开,竞技状态未达最佳,此时万万不可先做后面难题,做不顺手,会挫伤锐气和信心,切忌长时间思考一道难题,从而使容易得分的题目没有时间去做,顾此失彼,拣芝麻丢西瓜.如果从容易题、基本题做起,做顺几道题后,能解除紧张,增强信心,活跃思维,那么后面的所谓难题也就不难了.
⑵人易我易,我不能大意,最容易得分的,也是最容易失分的.
遇到容易题、相似题,切忌“乐”中出错,“乐”极生悲,要知道容易题更容易错,而且错了难查,不易发现,似曾相识只一字之差,解法也可能会完全不同.如:k为何值时,方程kx2-2x+3=0有实根?这样的题目只要细心加认真就能夺高分.
⑶人难我难,我不能畏难.
我难人更难,经过从初一到初三的多次较量,数学成绩我们一直居于全县前列.如果遇到较难综合题,正是我们各位同学与其他各校拉大分数差距的机会来了,只要你不畏难,不纠缠难题,依照平时复习中解综合题的策略,你至少比别人多拿几分,命题人把思考时间都计算在内了.切记:难题尽量放到最后去攻克.科学分配答题时间,专心致志,集中思考,排除干扰,沉着冷静,要充满自信但又不要盲目自信……,相信各位同学能超水平地发挥.
⑷仔细审题,先易后难
审题是答题的必要条件,既要看清题目的显性条件,更要注意字里行间的隐性条件,对每一个符号、数据、图形、图表等都要准确把握,然后联想已有的知识、识别题型、选择适当的方法,切记“正确的审题是成功的一半,而错误的审题则意味着全题覆没”,“注意答案就在题目上”这一至理名言对你的中考成功是至关重要的.
⑸卷面整洁,不留空白
答卷要从左到右,从上到下书写,排版合理,保持整洁,便于老师阅卷,在对有把握的试题准确无误地答完后,对把握不大的试题也要尽力思考,会一步答一步,实在无把握的也要根据“已知→可知,求证→需知”的八字思维方针尝试回答,尽量不留空白,这样就创造了得分机会,争取了得分机会.
⑹专心致志,集中思考
考试时要抛开一切与答题无关的杂念,高度集中注意力,不管你考得怎样,必须自始自终地全神贯注地投入考试,如果这时浮想联翩,必然耽误考试.
⑺排除干扰,沉着冷静
考试时的干扰主要来自两个方面:一是情绪干扰.由于过分紧张、焦虑而干扰对知识的回忆,使本来熟悉的知识难于再现,出现提笔忘字,甚至头脑中“一片空白”的现象,这时一定要平静下来,自我减压,使心态恢复正常.二是思维定势的干扰.如遇到“似曾相识”的问题,容易套用过去解答该类题型的方法,而忽略了题目之间的差异,有时最先想到的解法尽管不适用,却总不舍得抛开,妨碍其他方法的选择应用,遇到这种情况时,应暂时抛开此题,先做其他题目或换个角度思考,另作尝试,以求顺解.
⑻科学使用草稿纸、刻度尺、量角器等考试用具,力争超水平发挥,积小胜为大胜.
三、审题的方法和策略
审题就是弄清问题,是解题者在思维的参与下对题目提供的信息的发现、辨认和转译,并对信息作有序记录,明确要做什么事,在解数学题中,审题是至关重要的一步,学会正确审题,有利于很快找到解题的思路.
(一)审题,首先要强调仔细,弄清题目结构,明确题目实质.
仔细是审题中最重要的策略,数学语言的表达往往是十分精确,并具有特定的意义,审题时,就要仔细看清题目的每一个字、词、句,甚至每一个标点符号,只有领会其确切的含意,才能寻找解题的突破口,叩开解答之门.
例1:直线与x轴、y轴分别交于点A和点B,M是OB上一点,若将△ABM沿AM折叠,点B恰好落在x轴上的点B′处,则直线AM的解析式为_________________________.
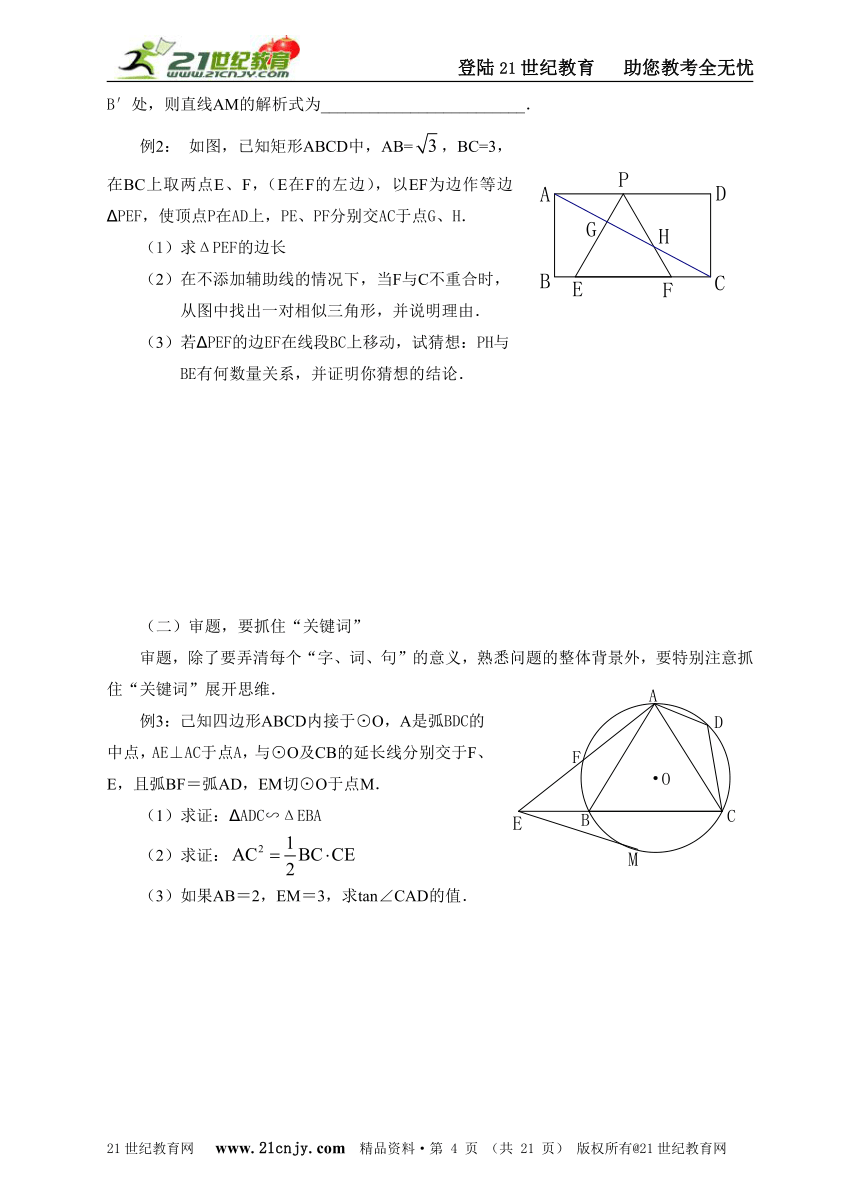
例2: 如图,已知矩形ABCD中,AB=,BC=3,在BC上取两点E、F,(E在F的左边),以EF为边作等边ΔPEF,使顶点P在AD上,PE、PF分别交AC于点G、H.
(1)求ΔPEF的边长
(2)在不添加辅助线的情况下,当F与C不重合时,
从图中找出一对相似三角形,并说明理由.
(3)若ΔPEF的边EF在线段BC上移动,试猜想:PH与
BE有何数量关系,并证明你猜想的结论.
(二)审题,要抓住“关键词”
审题,除了要弄清每个“字、词、句”的意义,熟悉问题的整体背景外,要特别注意抓住“关键词”展开思维.
例3:己知四边形ABCD内接于⊙O,A是弧BDC的中点,AE⊥AC于点A,与⊙O及CB的延长线分别交于F、E,且弧BF=弧AD,EM切⊙O于点M.
(1)求证:ΔADC∽ΔEBA
(2)求证:
(3)如果AB=2,EM=3,求tan∠CAD的值.
例4:已知关于x的方程(a-2)x2-(2a-1)x+a=0有实根,求a的值.
分析:关于x的方程未指明次数,有实根未指明有几个,关键词是“关于x的方程”、“有实根”.
(三)审题,要善于挖掘隐含条件
有些题目的已知条件比较复杂或不明显,审题时,就要善于挖掘隐含条件,还其庐山真面目,隐含条件一旦暴露,便为解题提供了新的信息和依据,解题思路也就伴随而生.
例5:⊙O1和⊙O2相交于点A、B,已知⊙O1的半径是2,⊙O2的半径是4,且AB=4,则O1O2=___________.
分析:本题应正确画出图形,考虑AB=4,⊙O1半径是2,⊙O1的圆心O1是AB的中点,从而O1O2=
如果没有挖掘上述隐含条件,按常规思维画出图形,就会产生斜边等于直角边的错误.
例6:己知关于x的一元二次方程有两个不相等的实数根,求K的值.()
例7 :化简:(1) (2)
(四)审题,还要注意“转换”与“识别”
对需要构造具体的数学模型来解的题目,审题时要注意“转换”与“识别”,把比较含蓄的信息转译为自己熟悉的便于理解的信息.
例8:ΔABC中,若AC、BC边的长是关于x的方程的两个根,且25BCsinA=9AB,求ΔABC三边的长.
(五)审题,要学会探索,大胆展开思维
解题,常常会困惑于找不到突破口,此时可考虑从特殊的点、特殊的值、特殊的图形等出发进行试探,取得部分成果,发现规律,从而获得解题途径.
例9:如图,直角梯形ABCD中,AB=7,∠B=90°,
BC-AD=1,以CD为直径的圆与AB有两个不同的公共点E、F,且AE=1,试问:在线段AB上是否存在P点,使得以P、A、D为顶点的三角形和以P、B、C 为顶点的三角形相似?若不存在,说明理由;若存在,这样的P点有几个,并算出AP的长度.
分析:直径CD对的角是直角,首先可挖掘符合条件的特殊点E和F,显然ΔAED∽ΔBEC,且AE=1,AF=6,其次是由数据的信息可求出AD=2,BC=3,再次是寻找异于E、F且符合条件的点,由于∠DPC≠90°,只有当∠APD=∠BPC时,ΔPAD∽ΔPBC,从而 AP=2.8,满足以上条件的P点有三个:AP长分别是1,6,2.8.
从以上例题可见,解数学题时,应对提供的信息反复推敲,如果看一遍还把握不住题意,抓不住关键,要有耐心接着看第二遍、第三遍,并且在解题过程中,甚至在求出了解以后,还需要看题和审题,即审题要贯穿于解题的全过程.
(六)根据题意画出草图
中考中的最后一题大多要用数形结合的思想,例子就不举了,华罗庚说得好:“数形结合无限好,许多问题解决了.”各位同学一定要养成好的习惯,做好文字语言、图形语言、符号语言之间的互译工作,培养认真的审题习惯,提高审题能力,在审题中学会动脑筋,学会具体问题具体分析,不断提高数学素养.
四、如何解题
要想提高解题能力,就得多做多练多思考多总结,从而掌握解题规律,解数学题一般可归纳为以下八个步骤:
1、审题
题目到手,不要急忙去做,要先认真阅读,弄清题意,挖掘题目中的隐含条件,必要时列出要点.弄清两个问题:
⑴这是什么类型的考题?是叙述题、求解题、作图题、计算题还是证明题、开放性题、应用数学题?
⑵题设条件是什么?哪些是显条件?哪些是隐条件?需要求什么?求的问题是一个还是几个?再简单的问题也少不了审题这一步,至于如何审题?前面已叙述颇多,这里不再讲了.
2、画图(列表等)
解几何题,画图往往是不可少的,把符号语言、文字语言转化成图形语言,标上已知和未知元素,代数应用题有时也需要画图和列表等,以帮助理解题意,有关函数的问题更是如此,当然,并不是每一个题目都需要画图或列表的.
3、分析
分析寻找解题思路,这是最困难,最费事的一步,要选出突破口,无论是一点突破,还是多点突破都要融会贯通,一气呵成.如果解题思路明确,可以用“已知→可知”的顺推方法,逐步推导下去,直至得出结论,如果思路不太明确,可以“先逆后顺”,即用“求证→需知”,逐步向上逆推,两头向中间凑到沟通后再顺推下来,就是综合分析法.
4、解题
这一步是把解题的思路转化为具体的解题步骤,书写出来,解题过程不能跳跃,主要步骤不能省略,要使别人能看得懂,重要的依据要写出来,一般点到为止,如“根据勾股定理可得……”等,推而无理,算而无据的毛病要克服.总之,答案要正确,解题要合理,方法要简便,表达要清楚、严谨、规范、流畅、精练.书写要整齐划一,一式一行,等号对齐,不能眉毛胡子连在一起,或者勾画得很乱,叫人看不清,造成不应有的失分.
5、检查
题目解出后,还需检查,检查内容包括:⑴重新审题,以防审题有误;⑵解题过程是否有误,如特殊角三角函数值是否记错(可用画图法重推导),二次根式化简符号是否有误,正负号是否错等;⑶是否回答了题目的全部要求;⑷答案是否符合题意,如是方程问题,注意有无增、失根.其他题目,如填空题、选择题是否是两解问题,解题中有无必要分类讨论,有无漏解.
6、讨论
有些题目在某种情况下有解,某种情况下无解,有解的情况下,何时只有一解,何时有若干个解,何时有无数个解,这都是讨论的内容,还要注意对个别特殊情况的讨论.
7、答题
答题就是写出题目确切的答案,对于文字题,应写出:“答”;对开放性试题应先写结论,再写理由,最后仍要交待一下结论;对于分式方程、无理方程一定要检验;对于一般习题,只要把答案以某种形式明确一下即可;对于多解等一定要反过来检验后再确定最后结果;对于压轴题中的分类讨论,先分类,再综合写出最后结果.
8、小结
写出答案后,解题已结束.对于平时的解题,还要做一个小结:这样的解法是否最简便?有没有更好的解法?从这题的解法,你会有哪些体会?
下面通过例题来说明以上八个步骤
例10:如图,在矩形ABCD中,AB=3,BC=4,BC是
⊙O的直径,P是AD上的一个动点,PB交⊙O于Q,设BP=x,CQ=y
⑴求y与x之间的函数关系式;⑵画出所求函数的图象.
①审题:这是一个求解题和画图题,要求y与x的函数关系式,并画出图象.
②画图:题目已给出图形,只要标出已知、未知元素即可.
③分析:题目首先要求找到y与x之间的关系,y在RtΔCQB中,x在RtΔBAP中,显然,问题要从研究这两个直角三角形的性质入手.
④解题:⑴在矩形ABCD中
AD∥BC,∠A=90°
∴∠APB=∠QBC
∵BC是直径
∴∠BQC=90°
易证RtΔBAP∽RtΔCQB
从图上可看出,AB<BP<BD,即3<BP<5
⑵所求函数图象是双曲线y= 在第一象限中的一段,不含两端点
⑤检查:题目要求的两个问题均已回答,解题中假定P点不与A、D重合,至于P点与A、D重合的情形,留待下面讨论解决.
⑥讨论
i.当P点与A重合时,x=AB=3, y=CB=4, 函数图象为点P1(3, 4)
ii.当P点与D重合时,x=BD=5, y=QC=,函数图象为点P2(5,2.4)
考虑到这两个特殊点,所求函数y= (3≤x≤5)的图象如下:
⑦答题:解题过程中已明确给出,最后不必再写.
⑧小结:本题关键是掌握好P点的位置,P点不与A、D重合是一般情况,需要详细解答,与A、D重合是特殊情况,不可省略.
解题八步,是就一般解题过程而言,实际解题时,其中有些步骤可以省略,在需要的步骤中,有的需要写出,有的虽有思维过程,但并不需要都写出,这些都要由实际情况而定.
五、中考各题型解题策略
(一)、解好填空题
填空题是中考的主要题型,占分36分左右,它考查目标明确,知识覆盖面广,评卷正确迅速,有利考查学生的分析判断能力和计算能力,而且填空题没有答案,可以防止学生猜估答案.通过历年中考考试卷分析,填空题失分率要比选择题高,特别注意最后一、二题小高潮题,一般要分类讨论,现通过实例谈谈解填空题的一般思路与解题技巧.
⑴直接法:直接从题设出发,运用定义、定理、公理、法则等去推理计算直接得出结论,如2-的倒数的相反数是___________.-1,-2,0,1,2的极差为_______,方差为_________.
⑵特殊值法:如a>0,b>0,且a-b<0,则将a,b,-a,-b从小到大排列起来应是__________________.
⑶数形结合法:函数y=-2x+4的图象不经过 象限.
⑷猜想结论,逆推验证法
①在直角坐标中,⊙O的半径为1,直线与⊙O的位置关系是__________.
②若不等式组 无解,则实数a的取值范围是____________________.
⑸整体代入法:
如果、是一元二次方程为______
填充题小试:
1、函数的图象过点(0,1)则a=_______.
2、估算的值为________(保留两个有效数字,误差不大于0.05),并把在数轴上表示出来.
3、抛物线的图象过原点,则m=________.
4、直线y=2x+b-2不经过第二象限,则b的取值范围为_________.
5、.
(2)tan2α+tanα-2=0,则tanα=__________.
6、关于x的方程的解为负数,则m的取值范围为________.
7、数轴上点A表示的实数为与点A相邻的整数点分别表示实数_________.
8、平面直角坐标系内一正方形ABCD,A点坐标为(1,1),C点坐标为(2,2),若二次函数的图象经过正方形ABCD内部,则a的取值范围为_______.
9、已知x=-1是关于x的方程2x2+ax-a2=0的一个根,则a=_________.
10、等腰三角形一腰上的高与腰之比为,顶角的度数是__________.
11、已知二次函数y=x2-(2m-1)x+4m-7的图像必过一个定点的坐标为______.
12、如图,△ABC是边长为3的等边三角形,△BDC是等腰三角形且∠BDC=120°,以D为顶点作一个60°的角,使其两边分别交AB于点M,交AC于点N,连结MN,则△AMN的周长=______________.
(二)、解好选择题
选择题是中考的题型之一,占分20分左右,它具有题目小,容量大,知识覆盖面宽,解法灵活,评价客观等优点,解选择题时有时你会碰到一时拿不准,或是超出你的能力、范围的题目,只要不倒扣,猜测可以为你创造更多的得分机会,当你碰到一道对你毫无头绪的题目时,可先空在那里,在考试即将结束时利用复查时间,重新考虑,若仍无头绪,可填上你的第一感觉选中的代码,特别注意最后两道小高潮题,记住,千万别留空白,这种情况下的决策能力对于一个人事业的成功也是很重要的.
下面从实例谈选择题的解法:
⑴直接法
如:函数y=+(x-2)0自变量的取值范围是( )
A、x≥-1 B、x≥1 C、x≤1 D、x≥1且x≠2
又如:若x1, x2是方程x2-(k-2)x+(k2+3k+5)=0(k为整数)的两个实根,则的最大值是( )
A、19 B、18 C、5 D、不存在
再如:如图,在△ABC中,AD⊥BC,CE⊥AB,垂足分别为D、E,AD、CE交于点H,已知EH=EB=3,AE=4,则CH的长是( )
A、1 B、2 C、3 D、4
⑵排除法
如:已知c为实数,a>b,则下列不等式成立的是( )
A、ac>bc B、ac<bc C、ac2>bc2 D、ac2≥bc2
⑶特殊值法
若0<x<1,则x、x2、x3的大小关系是
A、x<x2<x3 B、x<x3<x2 C、x3<x2<x D、x2<x3<x
⑷观察分析法
如:设ΔABC三边长为a、b、c,a边上中线长为m,如果(b-c)(2m-a)(a+b-c)=0,那么ΔABC一定是( )
A、等腰三角形 B、直角三角形 C、等腰直角三角形 D、以上都不对
(5)图象法
如:⑴己知点A(-3,a),B(-1,b),C(3,c)都在反比例函数的图像上,则a、b、c的大小为( )
A、a>b> c B、c>b>a C、b>c>a D、c>a>b
⑵已知抛物线y=ax2+bx+c(a>0)的对称轴是直线x=-1,与x轴的一个交点为(x1,0),且0<x1<1,下列结论:①9a-3b+c>0 ②b<a ③3a+c>0其中正确结论的个数是( )
A、0 B、1 C、2 D、3
⑶y=的图像如图,则=+k的解最多有( )个
A、4 B、1 C、2 D、3
选择题解法相当灵活,解法又多,需要同学们熟练掌握方法、技巧,选择最佳解法,使解题又快又准确.
选择题小试
1、如图,正方形ABCD的边长为2,点E在AB边上,四边形EFGH是边长为1的正方形,设ΔACF的面积为S,则( )
A、S=2 B、S=2.4 C、S=4
D、S与BE的长度有关
2、 探索以下规律
根据规律,从2006~2008箭头方向图是( )
3、己知函数的图象如图,根据其中提
供的信息,可求得使y≥1成立的x的取值范围是( )
A、1≤x≤3 C、x≥-3
B、-3≤x≤1 D、x≤-1或x≥3
4、在直角梯形ABCD中,AB⊥BC,AD=1,BC=3,
CD=4,EF为梯形的中位线,DH为梯形的高,则下列结论
①∠BCD=60° ②四边形EHCF为菱形 ③SΔBEH=SΔCEH ④以AB为直径的圆与CD相切于点F,其中正确的个数为( )
A、4 B、3 C、2 D、1
5、ΔABC中,BC=4,以A为圆心,2为半径的⊙A与BC相切于点D交AB于E ,交AC于F,P是⊙A上的一点,且∠EPF=40°,则图中阴影部分的面积为( )
(三)、耐心细致做好解答题
1、计算、化简题的考查,不光能了解同学们对基本概念的理解、基本技能的掌握情况,而且可以进一步考查思维速度与运算能力,题目虽不难,但不少人由于麻痹大意,计算中出现特殊角的三角函数值记不得,分母有理化、去括号、正负号等错误,导致不必要的失分,岂不知,这里的失分会影响全局,因此这方面题目要高度重视.如:
⑴
⑵
⑶-42+-(2008-)0+
⑷先化简,再求值 ,其中a满足a2-a=0
2、方程(组)、不等式(组)的考查,也是中考的一个重点.如:
(1)解方程 (2)解不等式组并把解集在数轴上表示
3、判别式与韦达定理是中考必考内容,应用很广泛
⑴应用判别式,韦达定理时,先把方程化成一般式
⑵应用判别式的前提是二次项系数a≠0
⑶应用韦达定理的前提是Δ≥0
⑷利用两根和、积求出某些字母值时,一定要代入判别式检验
⑸不能忽视两根和与积之间的制约关系 如:
①已知方程x2+(2k+1)x+k2-2=0的两实根的平方和等于11,求k的值.
②求实数m,使y=mx2-mx+1>0恒成立(分m=0、m≠0两种情况讨论).
4、三个二次的关系是重点
⑴三角形与二次三项式①②
⑵三角形与一元二次方程
⑶三角形与二次函数
⑷韦达定理与二次函数
⑸整系数一元二次方程有有理数根、整数根,△必定是一个完全平方式. 如:
①分解因式:x2-x-6=___________________________.
②m为何值时,x2+2x-2+m(x2-2x+1)是一个完全平方式?
③对于x的任何实数值,二次函数y=(m-1)x2-mx+m-1的值均为负,m的取值范围是_______________________.
5、平面几何中常见辅助线
⑴作特殊点的连线(直角顶点、斜边中点、等腰三角形底边上中点,正方形对角线交点,切点、圆心、外心、内心、梯形一腰中点、线段中点)
⑵作平行线
a. 已知一边中点,过中点作平行线
b. 作第四比例项得比例线段
c. 从比例的关键点作平行线
d. 作平移变换(梯形中平移腰、平移对角线等)
⑶平分或加倍
a. 作角平分线
b.加倍,折半
c.利用面积证
⑷作切线、公共弦、连心线等
如:综合试卷中几何题(略)
6、关于应用数学题、几何计算证明题,这类题目不仅需要解出结果,还要列出解题过程,审题显得尤为重要,做题注意以下几点:一是注意完成题目的全部要求,不遗漏;二是注意规范答题;三是注意不跳步;四是注意在试卷上记录步骤.
7、怎样解综合题
⑴审题:要充分利用已知条件,寻找隐含条件及其相互关系.
⑵设想:目的是寻求解题途径,设想的方法主要是“由因导果”、“执果索因”,也就是从命题的题设和结论出发接通思路,进行分析推导.
⑶突破:一道较难的综合题一般都有一两个难点,难点突破了,就会使一潭死水变活,这种突破靠的是坚实的数学基础,但更需要掌握和灵活运用常用的教学方法,如联想、类比、特例探路,辅助设元,待定系数,分析转化等方法.
⑷表述:综合题一般表述较多,涉及知识点和方法也多,一旦分析成功,难点突破后,要对试题的表述有一整体设计,先写什么,后写什么,每个层次的因果关系,都要清楚明白,准确完整,不重不漏.
⑸检查:这是保证解题成功的主要层次,检查常分为逐步检查、定性检查、定量检查等.
8、解综合题的几种策略
⑴步步递推,两面夹攻法
拿到一个综合题,从结论出发,利用“要证……只要证……”的思考模式,步步递推,顺藤摸瓜,当递推碰到困难时,可从条件出发,即“已知……可知……再可知”,这样从条件与结论两面夹攻,使问题最终得到解决.
⑵化整为零,各个击破
解综合题时,要对症下药,还其本来面目,将一个综合题拆成若干个基本题来解,命题人在出综合题时,是把几个基本题有机推砌成综合题,而解综合题时,则要把它分拆开来,要善于应用问题的条件与结论将它拆成几个相互联系的基本题,使问题逐一解决,从而实现各个击破,这是最基本且最有效的方法.
⑶调换角度,转化问题
在解综合题时,往往碰到思考过程受阻,这时我们可以换个角度看问题,则有时会打破僵局,找到希望之所在.转化的一般方法是:类比、变形、换元、添线、数形结合;转化的依据是学过的定义、定理、公理、公式及命题综合的条件;转化的指导思想是化抽象为具体、化复杂为简单、化新命题为旧命题.注意分类讨论(满分法)因为同学们这些日子综合题做得较多,对上述策略也有体会,不妨在考前选几条再试一试.
例:连接着汉口集家咀和汉阳南岸咀的江汉三桥(晴川桥),是一座下承式钢管混凝土系杆拱桥。它犹如一道美丽的彩虹跨越汉江,是江城武汉的一道靓丽景观。桥的拱肋ACB视为抛物线的一部分,桥面(视为水平的)与拱肋用垂直于桥面的系杆连接,相邻系杆之间的间距均为5米(不考虑系杆的粗细),拱肋的跨度AB为280米,距离拱肋的右端70米处的系杆EF的长度为42米.以AB所在直线为x轴,抛物线的对称轴为y轴建立如图②所示的平面直角坐标系.
(1)求抛物线的解析式;
(2)正中间系杆OC的长度是多少米?是否存在一根系杆的长度恰好是OC长度的一半?请说明理由。
六、答卷常见错误及分析
(一)、粗枝大叶,审题马虎,随意答题
例1:等腰三角形一腰上中线,将周长分为6和15两部分,求此等腰三角形的边长.这个等腰三角形边长为4,4,13 或10,10,1(但4+4<13,应舍去)
例2 :如果x2+kxy+9y2是一个完全平方式,那么k=________________.(如填“6”就中套了.)
(二)、基本图形不熟悉,错解或漏解
例3:⊙O1和⊙O2相交,公共弦长为24,⊙O1和⊙O2半径为13和15,求圆心距O1O2的长.答案:_________________________
(三)、忽视隐含条件,造成错解或漏解
例4:方程kx2-(2k+1)x+k=0有两个不相等实根,则k的取值范围是_________.
例5:ab<0时,化简=_____________________.
例6:一次函数y=kx+b的自变量的取值范围是-3≤x≤6,相应函数值的取值范围是-5≤y≤-2,则这个函数的解析式是_______________________.
例7:已知方程x2+(m-2)x+(5-m)=0的两根都比2大,求m的范围.
(四)、思维定向,影响解题
例8:⊙O1和⊙O2的半径分别为R1、R2且R1、R2是方程x2-4x+3=0的两根,且圆心距d=6, 则⊙O1与⊙O2的位置关系是__________________.
例9:直角三角形中已知两边长为3和4, 求第三边的长及内切圆的半径.
例10:已知锐角三角形边长为2,3,x,第三边x的取值范围是______________.
(五)、过去中考中典型错误评析
1、关于基础知识
⑴概念、公式、法则遗忘
⑵应用概念、公式、法则思维僵化
2、关于计算技能
⑴运算不正确的
⑵运算中不能及时作出自我判断、纠正错误
如:抛物线y=ax2+bx-1经过(2,1),且y最小值=-3,求出a<0后,不会根据有y最小值推出a>0,自行纠错.
3、关于思维方法
⑴思维缺策略,解题思路不灵活,如抛物线求出顶点后,已知三个点,不会根据抛物线对称性作图.
⑵思维不严谨,不注意隐含条件,零陷阱等.
⑶逆向思维不熟,又粗心.
4、关于数学问题信息的获取、加工、运用不能贯穿于解题始终.
⑴问题中信息未能充分挖掘,有些信息比较微弱,不能敏锐发现,使之转化为条件.
⑵不会信息加工——联想和推理,不会运用“已有信息——产生新信息——指引解题”的方法.
⑶不善于观察,不勤于观察,只会生搬硬套.
5、解题不规范
⑴分式方程、无理方程缺检验.
⑵应用性问题缺答和单位.
⑶设未知数不完整.
⑷计算跳步,运算错误.
⑸几何证明过程不完整,跳步.
⑹论证繁琐,书写马虎.
七、介绍几种防止失误的方法
(一)、分析条件要仔细缜密
由于隐含条件的隐蔽性强,不易察觉,所以在分析条件时,必须仔细缜密,使错误消除在解题之初.
如:把4x2+1加上一个单项式,使其成为完全平方式,写出所有符合条件的单项式.(错解4x或-4x)
(二)、解题过程要规范完备
某些隐含条件往往隐含在解题过程中,极易导致解题失误,所以必须强调解题过程规范完备,以防错解漏解.
如:己知不等式组无解,则a的取值范围________.(错解:a<-1)
(三)、解题结果要认真检验
某些隐含条件导致的解题错误,在分析条件和解题过程中,均不易发觉和避免,而必须对解得的结果予以检验,以消除错解,保证解题结果的正确性.
如:(1)已知抛物线y=x2+(k-2)x+1与x轴相交于A(a,0),B(b,0)两点,且k2-(a2+ka+1)(b2+kb+1)=0,求k值.
(2)若y关于x的函数y=(a-2)2-(2a-1)x=a的图像与坐标轴有两个交点,则a的范围是____________.(错解:a>,且a≠2)
一般在求二次函数、方程的待定系数或解分式方程时,都应检验结果的正确与否.
(四)、缜密思考,防止漏解
1、由于思维定势的束缚,引起漏解.
如:⑴已知线段AB=8cm,在直线AB上画线段BC,使它等于3cm,求线段AC的长.
⑵甲乙两站相距360km,上午9点15分一辆慢车和一辆快车分别从两站相向开往对方车站,经过3小时相遇,已知快车速度是慢车的1.5倍,试问两车在什么时刻相距90km?
⑶已知方程(a-1)x2=(a+1)xa有实数根,求a的取值范围.
(4)一组数据5、7、7、x,中位数与平均数相等,则x值为_________.(错解:9)
2、由于知识的盲点引起漏解
由于学习新知识时,缺乏创新思考,对所学知识不能举一反三,触类旁通,造成知识上的盲点,在解题时易出现漏解.
如:有三条两两相交(不交于一点)的公路,要修一座加油站,使其到三条公路距离相等,试确定加油站的站址.
3、对定理理解不透彻,引起漏解
要克服漏解现象,在学习过程中调动积极性、拓宽思维,发展创造思维能力,严密思考,迅速完整解题.
4、由于知识的综合运用能力的缺陷,引起漏解
如:已知二次函数y=-x2+2x+3的图象与x轴从左到右交于A、B两点,一次函数y=kx+b的图象经过点A与这个函数的图象交于另一点C,且SΔABC=8,求一次函数的解析式.
易错题演习:
⑴、为美化环境,计划在某小区内用30m2的草皮铺设一条边长10m的等腰三角形绿地,求出这个等腰三角形绿地的另外两边长.
⑵、若⊙O的直径AB为2,弦AC为,弦AD为,则S扇形OCD(其中2S扇形OCD<S⊙O)为______________.
⑶、直角三角形两边长分别为6和8,那么这个三角形外接圆半径等于_____________.
⑷、关于x的方程的一个根为0,则a的值是_________.
⑸、关于x的不等式组无解,则m的取值范围是_________.
⑹、半径为2㎝的圆内接ΔABC中,BC=2㎝,则∠A的度数为________.
⑺、平面内有线段AB和直线l,点A、B到直线l的距离分别是4㎝和6㎝,则线段AB的中点P到直线l的距离是________.
(8)、如图:直角ΔABC中,∠C=90°,AC=3,BC=4,若以C为圆心,R为半径所作的圆与斜边AB只有一个公共点,则R的取值范围是______________.
八、注意数学思想在解题中的应用
1、方程思想
己知如图,在ΔABC中,∠C=90°,D在BC上, BD=6,AD=BC,cos∠ADC=,则DC的长为_____.
2、函数思想
(1)如图,正方形ABCD的边长为4㎝,A是BC上不与B、C重合的任意一点,连接AP,过点P作PQ⊥AP交DC于Q,设BP的长为x㎝,CQ的长为y㎝,
①求点P在BC上运动的过程中, y的最大值;
②当y=㎝时,求x的值.
(2)有一块直角三角形的木板,∠C=90°,AB=5, BC=3,将它加工成一个面积最大的正方形木板,设计一种方案,并求出这个正方形木板的边长.
3、分类思想
己知关于x的函数的图象与x轴有交点,求a的取值范围.
4、化归思想
如图:在梯形ABCD中,AD∥BC,AB=CD,对角线AC、BD相交于点O,且AC⊥BD,AD=3, BC=5,求AC的长.
5、数形结合思想
(1)已知:点A(-1,-1)在抛物线y=(k2-1)x2-2(k-2)x+1上
①求抛物线的对称轴
②若B与A关于抛物线的对称轴对称,问是否存在与抛物线只交于一点B的直线?如果存在,求符合条件的直线?如果不存在,说明理由.
(2)如图①,⊙O的弦CD垂直于直径AB,垂足为点G,点E在弧CB上,作直线CE、ED与直线AB分别交于点F、M,连接OC,求证:OC2=OM·OF
如图②,把①中的“点E在弧CB上”改为“E在弧AD上”其余条件不变(如图),试问①中的结论是否成立?并说明理由.
九、认真复查
复查是交卷之前的最后一道工序,认真进行复查,能有效提高考试成绩.
首先应当纠正笔误,大家都有体验:有时我们做题时心里想的是某一内容,而同时笔下写的却是另一内容,这就是笔误.这种情况特别是几何论证中出现的较多,有时错写一个字母,自己还不知道,但对解题却影响极大,清除笔误一般只要认真核查一遍就行了.
其次要纠正算误,一道题,我们的思路方法都是对的,只是具体数据的计算上出了错,这种纯计算上的失误导致丢分甚为可惜,因为这道题从根本上讲你是会做的,应该拿满分,纠正算误的方法不仅仅是重算一次,如果可能,争取换一种方式算,有经验的会计师会横累计、竖累计,为什么不照原来的算法再重算一次呢?因为如果你第一次在某处犯了错误,第二次在该处很可能再犯同样的错误(一个人要想在极短的时间内,在相同的条件下发现刚刚犯过的错误是很难的),换一种方式算就可以避免了.
另外,还要注意运用所学知识去检验,比如+、-、×、÷、乘方、开方可以互相验算,因式分解可以用多项式的乘法验算,解方程(组)可以把结果代入原方程或方程组中去验算,几何题可以考察推理是否恰当,理由是否充足等等.
最后,还要仔细复查全卷,中考是规定时间内的竞争,复查时应重新审题,多角度、多思路考虑,如确定需要改,又经过深思熟虑后,才能擦去原题答案,以免失去得分机会.方法有:a.观察估计法;b.特例检查法;c.简单化检查法;d.数形直观法;e.逻辑检查法;f.发散性检查法等.这样既拿小分,又争大分,就有希望得满分.对比较隐蔽的错误,或是把握不大的答案,则要作综合分析.
十、了解评分标准
也许你没有写清所设未知数x的意义,扣1分.
也许你没有检验,扣1分.
如果没有最后的“答”这一步,再扣1分.
有的同学在解方程这一步就把不合题意的x2=-3去掉了,只写出原方程的一个解x=10,也要扣分.你看看,本来可以稳拿5分的题,结果只能得到2分,其它类型的题目也都存在类似的问题,应当按照标准的格式,认真写清每一个必要的步骤,千万不能随意省略关键性的步骤.
此外,不按要求答题,答案不写在指定位置,该带单位而不带单位或带错单位的也要扣分,作图题不保留作图痕迹,卷面不整洁等,都会导致丢冤枉分,考前了解评分标准,以避免不必要的失分.有时一分甚至半分之差,就会使你的结局由“重点”变为“普通”或由“计内”变为“择校”,说“一分值千金”丝毫也不夸张.
预祝同学们中考心想事成!万事如意!敬请各位同仁、同学们提出宝贵意见.
江苏省南通市港口中学 初三数学备课组 2012-3-28
考前指导是初中数学教学的最后一个环节.
经过3年的学习和紧张的几个月的复习准备后,同学们将要走进考场,实现自己的宏愿.但是能否将自己的实际水平如实地在考卷上全面正确地反映出来,除了要有扎实的知识功底外,还要掌握一些应考的策略技巧和必要的心理调适,注意应试技巧,尽量减少失误,考出最好成绩.
一、常见的心理障碍及其防治
有的同学临考时心情紧张,唯恐考不好,于是一些不良反应随之而来:如失眠、健忘、运算失误等,拿到卷子甚至头脑里一片空白,产生这种心理障碍的原因是对中考的功能及技巧策略不甚了解,中考除了对掌握的基础知识和技能进行测试外,同时也是一次心理素质和身体素质的测试.因此,心理上要有充分的准备,防治的方法主要有:
1、考前要有充分的时间休息,充分放松,出外散步,不开夜车,不做难题,不争辩等;
2、考场放松法是一种心理放松法,放松的原理是用紧张克服紧张,即用超觉静思法,使全身放松,平静心情,这样血液中含氧量充足,你必然会头脑清晰,自然就能超水平发挥.
3、必胜信心——精神胜利法,肯定的暗示会使自己发挥得更好.自己对自己说,我的能力超过试卷要求,我一定会考得很好,你也可以采取其它的肯定暗示语,这样自我表扬后,您的大脑为您的考试卖力工作,必然会取得理想成绩.
4、考前给自己看“病”,每一位考生在学习过程中都会存在这样或那样的“毛病”,这并不奇怪.但是在考前要努力把这些“毛病”治好.为此,你必须把自己做过的试题、试卷、笔记、错题集等重新看一遍,查一查那些没得分或被扣分的问题是怎么做的,做错的原因是什么,如果是因为知识没掌握,就要把这部分知识弄懂;如果是因为“粗心”,就要努力改变自己的不良习惯;如果是因为不会用正确的思想方法去分析问题、解决问题,那更要向老师、同学请教,并学习思考的方法,悟出道理;如果有别的同学请你“看病”,你更要认真地去“望闻问切”,以检验自己是否真会,增加一些“临床”经验.防止自己犯同样的“病”,考前给自己看病、治病,不带任何问题、任何疑点进考场,一定能收到意想不到的效果.
二、临场发挥策略技巧
搞好临场发挥是顺利通过中考最后一关的关键,这好比农民种田的收割季节,虽然农作物的长势很好,但如不能做到颗粒归仓,仍然得不到高产量.实际中,确有一些考生丢掉了本可以稳得的分数,非常令人遗憾.如何搞好临场发挥、提高应试技巧呢?
1、浏览全卷,把握全貌,科学分配答题时间.
⑴充分利用好考前5分钟,通读全卷,了解共有几页、正反面是否都有题目,如不全有,应及时反映给监考老师换卷子.试题类型、难易程度、每题的分值,对完成整卷自己所需的时间作一估计,如果估计比较乐观,答题时更要谨慎,因为有些题目看上去很简单,其实有命题人设置的陷阱等,如“零陷阱”,需要分类讨论,几何中的多解陷阱等;如果估计不乐观,那更要沉着对待,因为短时一瞥不是深思熟虑的结果,如果因此失去信心,就等于给自己设置障碍,减少成功机会.
⑵科学分配答卷时间的基本原则是保证在能得分的地方绝不失分,不易得分的地方争取得分,心目中要有分数时间比,如一道题目准备用3分钟,但3分钟过后一点眉目都没有,你可先跳开,但若已接近成功,延长一点时间也是必要的,分配时间,应保证考试成功的目的.
2、答题技巧:将试题分三批来做,力争一次性正确.
第一批是有把握做对的试题,这类题属“确保”范围,必须集中精力加以攻克,力争不失分,为保底的120—125分打下坚实的基础.
第二批是做心中有数但并非十分有把握的题目,这是“力争”范围,必须花力气突破,这样就可实现总分140分的目标,你有可能进入全县的前800名行列之中了.
第三批是做少数不太熟悉的题目,这时由于胜利在握,心情轻松愉快,思维畅通无阻,本来不会做的题目,你一定有可能做起来,有可能冲击满分,即使个别小题不会做,也要写上几步,多少也能拿点分,也不会影响考试全局,无非是帮其它科目少带了几分而己.
3、临场超水平发挥,必须遵循的原则
⑴先易后难,先简后繁,从前向后,步步为营,稳扎稳打,忌钻牛角尖和心算,循序渐进,这样有利于在考试中知识与技能的再现.
考试开始,因紧张手脑没有活动开,竞技状态未达最佳,此时万万不可先做后面难题,做不顺手,会挫伤锐气和信心,切忌长时间思考一道难题,从而使容易得分的题目没有时间去做,顾此失彼,拣芝麻丢西瓜.如果从容易题、基本题做起,做顺几道题后,能解除紧张,增强信心,活跃思维,那么后面的所谓难题也就不难了.
⑵人易我易,我不能大意,最容易得分的,也是最容易失分的.
遇到容易题、相似题,切忌“乐”中出错,“乐”极生悲,要知道容易题更容易错,而且错了难查,不易发现,似曾相识只一字之差,解法也可能会完全不同.如:k为何值时,方程kx2-2x+3=0有实根?这样的题目只要细心加认真就能夺高分.
⑶人难我难,我不能畏难.
我难人更难,经过从初一到初三的多次较量,数学成绩我们一直居于全县前列.如果遇到较难综合题,正是我们各位同学与其他各校拉大分数差距的机会来了,只要你不畏难,不纠缠难题,依照平时复习中解综合题的策略,你至少比别人多拿几分,命题人把思考时间都计算在内了.切记:难题尽量放到最后去攻克.科学分配答题时间,专心致志,集中思考,排除干扰,沉着冷静,要充满自信但又不要盲目自信……,相信各位同学能超水平地发挥.
⑷仔细审题,先易后难
审题是答题的必要条件,既要看清题目的显性条件,更要注意字里行间的隐性条件,对每一个符号、数据、图形、图表等都要准确把握,然后联想已有的知识、识别题型、选择适当的方法,切记“正确的审题是成功的一半,而错误的审题则意味着全题覆没”,“注意答案就在题目上”这一至理名言对你的中考成功是至关重要的.
⑸卷面整洁,不留空白
答卷要从左到右,从上到下书写,排版合理,保持整洁,便于老师阅卷,在对有把握的试题准确无误地答完后,对把握不大的试题也要尽力思考,会一步答一步,实在无把握的也要根据“已知→可知,求证→需知”的八字思维方针尝试回答,尽量不留空白,这样就创造了得分机会,争取了得分机会.
⑹专心致志,集中思考
考试时要抛开一切与答题无关的杂念,高度集中注意力,不管你考得怎样,必须自始自终地全神贯注地投入考试,如果这时浮想联翩,必然耽误考试.
⑺排除干扰,沉着冷静
考试时的干扰主要来自两个方面:一是情绪干扰.由于过分紧张、焦虑而干扰对知识的回忆,使本来熟悉的知识难于再现,出现提笔忘字,甚至头脑中“一片空白”的现象,这时一定要平静下来,自我减压,使心态恢复正常.二是思维定势的干扰.如遇到“似曾相识”的问题,容易套用过去解答该类题型的方法,而忽略了题目之间的差异,有时最先想到的解法尽管不适用,却总不舍得抛开,妨碍其他方法的选择应用,遇到这种情况时,应暂时抛开此题,先做其他题目或换个角度思考,另作尝试,以求顺解.
⑻科学使用草稿纸、刻度尺、量角器等考试用具,力争超水平发挥,积小胜为大胜.
三、审题的方法和策略
审题就是弄清问题,是解题者在思维的参与下对题目提供的信息的发现、辨认和转译,并对信息作有序记录,明确要做什么事,在解数学题中,审题是至关重要的一步,学会正确审题,有利于很快找到解题的思路.
(一)审题,首先要强调仔细,弄清题目结构,明确题目实质.
仔细是审题中最重要的策略,数学语言的表达往往是十分精确,并具有特定的意义,审题时,就要仔细看清题目的每一个字、词、句,甚至每一个标点符号,只有领会其确切的含意,才能寻找解题的突破口,叩开解答之门.
例1:直线与x轴、y轴分别交于点A和点B,M是OB上一点,若将△ABM沿AM折叠,点B恰好落在x轴上的点B′处,则直线AM的解析式为_________________________.
例2: 如图,已知矩形ABCD中,AB=,BC=3,在BC上取两点E、F,(E在F的左边),以EF为边作等边ΔPEF,使顶点P在AD上,PE、PF分别交AC于点G、H.
(1)求ΔPEF的边长
(2)在不添加辅助线的情况下,当F与C不重合时,
从图中找出一对相似三角形,并说明理由.
(3)若ΔPEF的边EF在线段BC上移动,试猜想:PH与
BE有何数量关系,并证明你猜想的结论.
(二)审题,要抓住“关键词”
审题,除了要弄清每个“字、词、句”的意义,熟悉问题的整体背景外,要特别注意抓住“关键词”展开思维.
例3:己知四边形ABCD内接于⊙O,A是弧BDC的中点,AE⊥AC于点A,与⊙O及CB的延长线分别交于F、E,且弧BF=弧AD,EM切⊙O于点M.
(1)求证:ΔADC∽ΔEBA
(2)求证:
(3)如果AB=2,EM=3,求tan∠CAD的值.
例4:已知关于x的方程(a-2)x2-(2a-1)x+a=0有实根,求a的值.
分析:关于x的方程未指明次数,有实根未指明有几个,关键词是“关于x的方程”、“有实根”.
(三)审题,要善于挖掘隐含条件
有些题目的已知条件比较复杂或不明显,审题时,就要善于挖掘隐含条件,还其庐山真面目,隐含条件一旦暴露,便为解题提供了新的信息和依据,解题思路也就伴随而生.
例5:⊙O1和⊙O2相交于点A、B,已知⊙O1的半径是2,⊙O2的半径是4,且AB=4,则O1O2=___________.
分析:本题应正确画出图形,考虑AB=4,⊙O1半径是2,⊙O1的圆心O1是AB的中点,从而O1O2=
如果没有挖掘上述隐含条件,按常规思维画出图形,就会产生斜边等于直角边的错误.
例6:己知关于x的一元二次方程有两个不相等的实数根,求K的值.()
例7 :化简:(1) (2)
(四)审题,还要注意“转换”与“识别”
对需要构造具体的数学模型来解的题目,审题时要注意“转换”与“识别”,把比较含蓄的信息转译为自己熟悉的便于理解的信息.
例8:ΔABC中,若AC、BC边的长是关于x的方程的两个根,且25BCsinA=9AB,求ΔABC三边的长.
(五)审题,要学会探索,大胆展开思维
解题,常常会困惑于找不到突破口,此时可考虑从特殊的点、特殊的值、特殊的图形等出发进行试探,取得部分成果,发现规律,从而获得解题途径.
例9:如图,直角梯形ABCD中,AB=7,∠B=90°,
BC-AD=1,以CD为直径的圆与AB有两个不同的公共点E、F,且AE=1,试问:在线段AB上是否存在P点,使得以P、A、D为顶点的三角形和以P、B、C 为顶点的三角形相似?若不存在,说明理由;若存在,这样的P点有几个,并算出AP的长度.
分析:直径CD对的角是直角,首先可挖掘符合条件的特殊点E和F,显然ΔAED∽ΔBEC,且AE=1,AF=6,其次是由数据的信息可求出AD=2,BC=3,再次是寻找异于E、F且符合条件的点,由于∠DPC≠90°,只有当∠APD=∠BPC时,ΔPAD∽ΔPBC,从而 AP=2.8,满足以上条件的P点有三个:AP长分别是1,6,2.8.
从以上例题可见,解数学题时,应对提供的信息反复推敲,如果看一遍还把握不住题意,抓不住关键,要有耐心接着看第二遍、第三遍,并且在解题过程中,甚至在求出了解以后,还需要看题和审题,即审题要贯穿于解题的全过程.
(六)根据题意画出草图
中考中的最后一题大多要用数形结合的思想,例子就不举了,华罗庚说得好:“数形结合无限好,许多问题解决了.”各位同学一定要养成好的习惯,做好文字语言、图形语言、符号语言之间的互译工作,培养认真的审题习惯,提高审题能力,在审题中学会动脑筋,学会具体问题具体分析,不断提高数学素养.
四、如何解题
要想提高解题能力,就得多做多练多思考多总结,从而掌握解题规律,解数学题一般可归纳为以下八个步骤:
1、审题
题目到手,不要急忙去做,要先认真阅读,弄清题意,挖掘题目中的隐含条件,必要时列出要点.弄清两个问题:
⑴这是什么类型的考题?是叙述题、求解题、作图题、计算题还是证明题、开放性题、应用数学题?
⑵题设条件是什么?哪些是显条件?哪些是隐条件?需要求什么?求的问题是一个还是几个?再简单的问题也少不了审题这一步,至于如何审题?前面已叙述颇多,这里不再讲了.
2、画图(列表等)
解几何题,画图往往是不可少的,把符号语言、文字语言转化成图形语言,标上已知和未知元素,代数应用题有时也需要画图和列表等,以帮助理解题意,有关函数的问题更是如此,当然,并不是每一个题目都需要画图或列表的.
3、分析
分析寻找解题思路,这是最困难,最费事的一步,要选出突破口,无论是一点突破,还是多点突破都要融会贯通,一气呵成.如果解题思路明确,可以用“已知→可知”的顺推方法,逐步推导下去,直至得出结论,如果思路不太明确,可以“先逆后顺”,即用“求证→需知”,逐步向上逆推,两头向中间凑到沟通后再顺推下来,就是综合分析法.
4、解题
这一步是把解题的思路转化为具体的解题步骤,书写出来,解题过程不能跳跃,主要步骤不能省略,要使别人能看得懂,重要的依据要写出来,一般点到为止,如“根据勾股定理可得……”等,推而无理,算而无据的毛病要克服.总之,答案要正确,解题要合理,方法要简便,表达要清楚、严谨、规范、流畅、精练.书写要整齐划一,一式一行,等号对齐,不能眉毛胡子连在一起,或者勾画得很乱,叫人看不清,造成不应有的失分.
5、检查
题目解出后,还需检查,检查内容包括:⑴重新审题,以防审题有误;⑵解题过程是否有误,如特殊角三角函数值是否记错(可用画图法重推导),二次根式化简符号是否有误,正负号是否错等;⑶是否回答了题目的全部要求;⑷答案是否符合题意,如是方程问题,注意有无增、失根.其他题目,如填空题、选择题是否是两解问题,解题中有无必要分类讨论,有无漏解.
6、讨论
有些题目在某种情况下有解,某种情况下无解,有解的情况下,何时只有一解,何时有若干个解,何时有无数个解,这都是讨论的内容,还要注意对个别特殊情况的讨论.
7、答题
答题就是写出题目确切的答案,对于文字题,应写出:“答”;对开放性试题应先写结论,再写理由,最后仍要交待一下结论;对于分式方程、无理方程一定要检验;对于一般习题,只要把答案以某种形式明确一下即可;对于多解等一定要反过来检验后再确定最后结果;对于压轴题中的分类讨论,先分类,再综合写出最后结果.
8、小结
写出答案后,解题已结束.对于平时的解题,还要做一个小结:这样的解法是否最简便?有没有更好的解法?从这题的解法,你会有哪些体会?
下面通过例题来说明以上八个步骤
例10:如图,在矩形ABCD中,AB=3,BC=4,BC是
⊙O的直径,P是AD上的一个动点,PB交⊙O于Q,设BP=x,CQ=y
⑴求y与x之间的函数关系式;⑵画出所求函数的图象.
①审题:这是一个求解题和画图题,要求y与x的函数关系式,并画出图象.
②画图:题目已给出图形,只要标出已知、未知元素即可.
③分析:题目首先要求找到y与x之间的关系,y在RtΔCQB中,x在RtΔBAP中,显然,问题要从研究这两个直角三角形的性质入手.
④解题:⑴在矩形ABCD中
AD∥BC,∠A=90°
∴∠APB=∠QBC
∵BC是直径
∴∠BQC=90°
易证RtΔBAP∽RtΔCQB
从图上可看出,AB<BP<BD,即3<BP<5
⑵所求函数图象是双曲线y= 在第一象限中的一段,不含两端点
⑤检查:题目要求的两个问题均已回答,解题中假定P点不与A、D重合,至于P点与A、D重合的情形,留待下面讨论解决.
⑥讨论
i.当P点与A重合时,x=AB=3, y=CB=4, 函数图象为点P1(3, 4)
ii.当P点与D重合时,x=BD=5, y=QC=,函数图象为点P2(5,2.4)
考虑到这两个特殊点,所求函数y= (3≤x≤5)的图象如下:
⑦答题:解题过程中已明确给出,最后不必再写.
⑧小结:本题关键是掌握好P点的位置,P点不与A、D重合是一般情况,需要详细解答,与A、D重合是特殊情况,不可省略.
解题八步,是就一般解题过程而言,实际解题时,其中有些步骤可以省略,在需要的步骤中,有的需要写出,有的虽有思维过程,但并不需要都写出,这些都要由实际情况而定.
五、中考各题型解题策略
(一)、解好填空题
填空题是中考的主要题型,占分36分左右,它考查目标明确,知识覆盖面广,评卷正确迅速,有利考查学生的分析判断能力和计算能力,而且填空题没有答案,可以防止学生猜估答案.通过历年中考考试卷分析,填空题失分率要比选择题高,特别注意最后一、二题小高潮题,一般要分类讨论,现通过实例谈谈解填空题的一般思路与解题技巧.
⑴直接法:直接从题设出发,运用定义、定理、公理、法则等去推理计算直接得出结论,如2-的倒数的相反数是___________.-1,-2,0,1,2的极差为_______,方差为_________.
⑵特殊值法:如a>0,b>0,且a-b<0,则将a,b,-a,-b从小到大排列起来应是__________________.
⑶数形结合法:函数y=-2x+4的图象不经过 象限.
⑷猜想结论,逆推验证法
①在直角坐标中,⊙O的半径为1,直线与⊙O的位置关系是__________.
②若不等式组 无解,则实数a的取值范围是____________________.
⑸整体代入法:
如果、是一元二次方程为______
填充题小试:
1、函数的图象过点(0,1)则a=_______.
2、估算的值为________(保留两个有效数字,误差不大于0.05),并把在数轴上表示出来.
3、抛物线的图象过原点,则m=________.
4、直线y=2x+b-2不经过第二象限,则b的取值范围为_________.
5、.
(2)tan2α+tanα-2=0,则tanα=__________.
6、关于x的方程的解为负数,则m的取值范围为________.
7、数轴上点A表示的实数为与点A相邻的整数点分别表示实数_________.
8、平面直角坐标系内一正方形ABCD,A点坐标为(1,1),C点坐标为(2,2),若二次函数的图象经过正方形ABCD内部,则a的取值范围为_______.
9、已知x=-1是关于x的方程2x2+ax-a2=0的一个根,则a=_________.
10、等腰三角形一腰上的高与腰之比为,顶角的度数是__________.
11、已知二次函数y=x2-(2m-1)x+4m-7的图像必过一个定点的坐标为______.
12、如图,△ABC是边长为3的等边三角形,△BDC是等腰三角形且∠BDC=120°,以D为顶点作一个60°的角,使其两边分别交AB于点M,交AC于点N,连结MN,则△AMN的周长=______________.
(二)、解好选择题
选择题是中考的题型之一,占分20分左右,它具有题目小,容量大,知识覆盖面宽,解法灵活,评价客观等优点,解选择题时有时你会碰到一时拿不准,或是超出你的能力、范围的题目,只要不倒扣,猜测可以为你创造更多的得分机会,当你碰到一道对你毫无头绪的题目时,可先空在那里,在考试即将结束时利用复查时间,重新考虑,若仍无头绪,可填上你的第一感觉选中的代码,特别注意最后两道小高潮题,记住,千万别留空白,这种情况下的决策能力对于一个人事业的成功也是很重要的.
下面从实例谈选择题的解法:
⑴直接法
如:函数y=+(x-2)0自变量的取值范围是( )
A、x≥-1 B、x≥1 C、x≤1 D、x≥1且x≠2
又如:若x1, x2是方程x2-(k-2)x+(k2+3k+5)=0(k为整数)的两个实根,则的最大值是( )
A、19 B、18 C、5 D、不存在
再如:如图,在△ABC中,AD⊥BC,CE⊥AB,垂足分别为D、E,AD、CE交于点H,已知EH=EB=3,AE=4,则CH的长是( )
A、1 B、2 C、3 D、4
⑵排除法
如:已知c为实数,a>b,则下列不等式成立的是( )
A、ac>bc B、ac<bc C、ac2>bc2 D、ac2≥bc2
⑶特殊值法
若0<x<1,则x、x2、x3的大小关系是
A、x<x2<x3 B、x<x3<x2 C、x3<x2<x D、x2<x3<x
⑷观察分析法
如:设ΔABC三边长为a、b、c,a边上中线长为m,如果(b-c)(2m-a)(a+b-c)=0,那么ΔABC一定是( )
A、等腰三角形 B、直角三角形 C、等腰直角三角形 D、以上都不对
(5)图象法
如:⑴己知点A(-3,a),B(-1,b),C(3,c)都在反比例函数的图像上,则a、b、c的大小为( )
A、a>b> c B、c>b>a C、b>c>a D、c>a>b
⑵已知抛物线y=ax2+bx+c(a>0)的对称轴是直线x=-1,与x轴的一个交点为(x1,0),且0<x1<1,下列结论:①9a-3b+c>0 ②b<a ③3a+c>0其中正确结论的个数是( )
A、0 B、1 C、2 D、3
⑶y=的图像如图,则=+k的解最多有( )个
A、4 B、1 C、2 D、3
选择题解法相当灵活,解法又多,需要同学们熟练掌握方法、技巧,选择最佳解法,使解题又快又准确.
选择题小试
1、如图,正方形ABCD的边长为2,点E在AB边上,四边形EFGH是边长为1的正方形,设ΔACF的面积为S,则( )
A、S=2 B、S=2.4 C、S=4
D、S与BE的长度有关
2、 探索以下规律
根据规律,从2006~2008箭头方向图是( )
3、己知函数的图象如图,根据其中提
供的信息,可求得使y≥1成立的x的取值范围是( )
A、1≤x≤3 C、x≥-3
B、-3≤x≤1 D、x≤-1或x≥3
4、在直角梯形ABCD中,AB⊥BC,AD=1,BC=3,
CD=4,EF为梯形的中位线,DH为梯形的高,则下列结论
①∠BCD=60° ②四边形EHCF为菱形 ③SΔBEH=SΔCEH ④以AB为直径的圆与CD相切于点F,其中正确的个数为( )
A、4 B、3 C、2 D、1
5、ΔABC中,BC=4,以A为圆心,2为半径的⊙A与BC相切于点D交AB于E ,交AC于F,P是⊙A上的一点,且∠EPF=40°,则图中阴影部分的面积为( )
(三)、耐心细致做好解答题
1、计算、化简题的考查,不光能了解同学们对基本概念的理解、基本技能的掌握情况,而且可以进一步考查思维速度与运算能力,题目虽不难,但不少人由于麻痹大意,计算中出现特殊角的三角函数值记不得,分母有理化、去括号、正负号等错误,导致不必要的失分,岂不知,这里的失分会影响全局,因此这方面题目要高度重视.如:
⑴
⑵
⑶-42+-(2008-)0+
⑷先化简,再求值 ,其中a满足a2-a=0
2、方程(组)、不等式(组)的考查,也是中考的一个重点.如:
(1)解方程 (2)解不等式组并把解集在数轴上表示
3、判别式与韦达定理是中考必考内容,应用很广泛
⑴应用判别式,韦达定理时,先把方程化成一般式
⑵应用判别式的前提是二次项系数a≠0
⑶应用韦达定理的前提是Δ≥0
⑷利用两根和、积求出某些字母值时,一定要代入判别式检验
⑸不能忽视两根和与积之间的制约关系 如:
①已知方程x2+(2k+1)x+k2-2=0的两实根的平方和等于11,求k的值.
②求实数m,使y=mx2-mx+1>0恒成立(分m=0、m≠0两种情况讨论).
4、三个二次的关系是重点
⑴三角形与二次三项式①②
⑵三角形与一元二次方程
⑶三角形与二次函数
⑷韦达定理与二次函数
⑸整系数一元二次方程有有理数根、整数根,△必定是一个完全平方式. 如:
①分解因式:x2-x-6=___________________________.
②m为何值时,x2+2x-2+m(x2-2x+1)是一个完全平方式?
③对于x的任何实数值,二次函数y=(m-1)x2-mx+m-1的值均为负,m的取值范围是_______________________.
5、平面几何中常见辅助线
⑴作特殊点的连线(直角顶点、斜边中点、等腰三角形底边上中点,正方形对角线交点,切点、圆心、外心、内心、梯形一腰中点、线段中点)
⑵作平行线
a. 已知一边中点,过中点作平行线
b. 作第四比例项得比例线段
c. 从比例的关键点作平行线
d. 作平移变换(梯形中平移腰、平移对角线等)
⑶平分或加倍
a. 作角平分线
b.加倍,折半
c.利用面积证
⑷作切线、公共弦、连心线等
如:综合试卷中几何题(略)
6、关于应用数学题、几何计算证明题,这类题目不仅需要解出结果,还要列出解题过程,审题显得尤为重要,做题注意以下几点:一是注意完成题目的全部要求,不遗漏;二是注意规范答题;三是注意不跳步;四是注意在试卷上记录步骤.
7、怎样解综合题
⑴审题:要充分利用已知条件,寻找隐含条件及其相互关系.
⑵设想:目的是寻求解题途径,设想的方法主要是“由因导果”、“执果索因”,也就是从命题的题设和结论出发接通思路,进行分析推导.
⑶突破:一道较难的综合题一般都有一两个难点,难点突破了,就会使一潭死水变活,这种突破靠的是坚实的数学基础,但更需要掌握和灵活运用常用的教学方法,如联想、类比、特例探路,辅助设元,待定系数,分析转化等方法.
⑷表述:综合题一般表述较多,涉及知识点和方法也多,一旦分析成功,难点突破后,要对试题的表述有一整体设计,先写什么,后写什么,每个层次的因果关系,都要清楚明白,准确完整,不重不漏.
⑸检查:这是保证解题成功的主要层次,检查常分为逐步检查、定性检查、定量检查等.
8、解综合题的几种策略
⑴步步递推,两面夹攻法
拿到一个综合题,从结论出发,利用“要证……只要证……”的思考模式,步步递推,顺藤摸瓜,当递推碰到困难时,可从条件出发,即“已知……可知……再可知”,这样从条件与结论两面夹攻,使问题最终得到解决.
⑵化整为零,各个击破
解综合题时,要对症下药,还其本来面目,将一个综合题拆成若干个基本题来解,命题人在出综合题时,是把几个基本题有机推砌成综合题,而解综合题时,则要把它分拆开来,要善于应用问题的条件与结论将它拆成几个相互联系的基本题,使问题逐一解决,从而实现各个击破,这是最基本且最有效的方法.
⑶调换角度,转化问题
在解综合题时,往往碰到思考过程受阻,这时我们可以换个角度看问题,则有时会打破僵局,找到希望之所在.转化的一般方法是:类比、变形、换元、添线、数形结合;转化的依据是学过的定义、定理、公理、公式及命题综合的条件;转化的指导思想是化抽象为具体、化复杂为简单、化新命题为旧命题.注意分类讨论(满分法)因为同学们这些日子综合题做得较多,对上述策略也有体会,不妨在考前选几条再试一试.
例:连接着汉口集家咀和汉阳南岸咀的江汉三桥(晴川桥),是一座下承式钢管混凝土系杆拱桥。它犹如一道美丽的彩虹跨越汉江,是江城武汉的一道靓丽景观。桥的拱肋ACB视为抛物线的一部分,桥面(视为水平的)与拱肋用垂直于桥面的系杆连接,相邻系杆之间的间距均为5米(不考虑系杆的粗细),拱肋的跨度AB为280米,距离拱肋的右端70米处的系杆EF的长度为42米.以AB所在直线为x轴,抛物线的对称轴为y轴建立如图②所示的平面直角坐标系.
(1)求抛物线的解析式;
(2)正中间系杆OC的长度是多少米?是否存在一根系杆的长度恰好是OC长度的一半?请说明理由。
六、答卷常见错误及分析
(一)、粗枝大叶,审题马虎,随意答题
例1:等腰三角形一腰上中线,将周长分为6和15两部分,求此等腰三角形的边长.这个等腰三角形边长为4,4,13 或10,10,1(但4+4<13,应舍去)
例2 :如果x2+kxy+9y2是一个完全平方式,那么k=________________.(如填“6”就中套了.)
(二)、基本图形不熟悉,错解或漏解
例3:⊙O1和⊙O2相交,公共弦长为24,⊙O1和⊙O2半径为13和15,求圆心距O1O2的长.答案:_________________________
(三)、忽视隐含条件,造成错解或漏解
例4:方程kx2-(2k+1)x+k=0有两个不相等实根,则k的取值范围是_________.
例5:ab<0时,化简=_____________________.
例6:一次函数y=kx+b的自变量的取值范围是-3≤x≤6,相应函数值的取值范围是-5≤y≤-2,则这个函数的解析式是_______________________.
例7:已知方程x2+(m-2)x+(5-m)=0的两根都比2大,求m的范围.
(四)、思维定向,影响解题
例8:⊙O1和⊙O2的半径分别为R1、R2且R1、R2是方程x2-4x+3=0的两根,且圆心距d=6, 则⊙O1与⊙O2的位置关系是__________________.
例9:直角三角形中已知两边长为3和4, 求第三边的长及内切圆的半径.
例10:已知锐角三角形边长为2,3,x,第三边x的取值范围是______________.
(五)、过去中考中典型错误评析
1、关于基础知识
⑴概念、公式、法则遗忘
⑵应用概念、公式、法则思维僵化
2、关于计算技能
⑴运算不正确的
⑵运算中不能及时作出自我判断、纠正错误
如:抛物线y=ax2+bx-1经过(2,1),且y最小值=-3,求出a<0后,不会根据有y最小值推出a>0,自行纠错.
3、关于思维方法
⑴思维缺策略,解题思路不灵活,如抛物线求出顶点后,已知三个点,不会根据抛物线对称性作图.
⑵思维不严谨,不注意隐含条件,零陷阱等.
⑶逆向思维不熟,又粗心.
4、关于数学问题信息的获取、加工、运用不能贯穿于解题始终.
⑴问题中信息未能充分挖掘,有些信息比较微弱,不能敏锐发现,使之转化为条件.
⑵不会信息加工——联想和推理,不会运用“已有信息——产生新信息——指引解题”的方法.
⑶不善于观察,不勤于观察,只会生搬硬套.
5、解题不规范
⑴分式方程、无理方程缺检验.
⑵应用性问题缺答和单位.
⑶设未知数不完整.
⑷计算跳步,运算错误.
⑸几何证明过程不完整,跳步.
⑹论证繁琐,书写马虎.
七、介绍几种防止失误的方法
(一)、分析条件要仔细缜密
由于隐含条件的隐蔽性强,不易察觉,所以在分析条件时,必须仔细缜密,使错误消除在解题之初.
如:把4x2+1加上一个单项式,使其成为完全平方式,写出所有符合条件的单项式.(错解4x或-4x)
(二)、解题过程要规范完备
某些隐含条件往往隐含在解题过程中,极易导致解题失误,所以必须强调解题过程规范完备,以防错解漏解.
如:己知不等式组无解,则a的取值范围________.(错解:a<-1)
(三)、解题结果要认真检验
某些隐含条件导致的解题错误,在分析条件和解题过程中,均不易发觉和避免,而必须对解得的结果予以检验,以消除错解,保证解题结果的正确性.
如:(1)已知抛物线y=x2+(k-2)x+1与x轴相交于A(a,0),B(b,0)两点,且k2-(a2+ka+1)(b2+kb+1)=0,求k值.
(2)若y关于x的函数y=(a-2)2-(2a-1)x=a的图像与坐标轴有两个交点,则a的范围是____________.(错解:a>,且a≠2)
一般在求二次函数、方程的待定系数或解分式方程时,都应检验结果的正确与否.
(四)、缜密思考,防止漏解
1、由于思维定势的束缚,引起漏解.
如:⑴已知线段AB=8cm,在直线AB上画线段BC,使它等于3cm,求线段AC的长.
⑵甲乙两站相距360km,上午9点15分一辆慢车和一辆快车分别从两站相向开往对方车站,经过3小时相遇,已知快车速度是慢车的1.5倍,试问两车在什么时刻相距90km?
⑶已知方程(a-1)x2=(a+1)xa有实数根,求a的取值范围.
(4)一组数据5、7、7、x,中位数与平均数相等,则x值为_________.(错解:9)
2、由于知识的盲点引起漏解
由于学习新知识时,缺乏创新思考,对所学知识不能举一反三,触类旁通,造成知识上的盲点,在解题时易出现漏解.
如:有三条两两相交(不交于一点)的公路,要修一座加油站,使其到三条公路距离相等,试确定加油站的站址.
3、对定理理解不透彻,引起漏解
要克服漏解现象,在学习过程中调动积极性、拓宽思维,发展创造思维能力,严密思考,迅速完整解题.
4、由于知识的综合运用能力的缺陷,引起漏解
如:已知二次函数y=-x2+2x+3的图象与x轴从左到右交于A、B两点,一次函数y=kx+b的图象经过点A与这个函数的图象交于另一点C,且SΔABC=8,求一次函数的解析式.
易错题演习:
⑴、为美化环境,计划在某小区内用30m2的草皮铺设一条边长10m的等腰三角形绿地,求出这个等腰三角形绿地的另外两边长.
⑵、若⊙O的直径AB为2,弦AC为,弦AD为,则S扇形OCD(其中2S扇形OCD<S⊙O)为______________.
⑶、直角三角形两边长分别为6和8,那么这个三角形外接圆半径等于_____________.
⑷、关于x的方程的一个根为0,则a的值是_________.
⑸、关于x的不等式组无解,则m的取值范围是_________.
⑹、半径为2㎝的圆内接ΔABC中,BC=2㎝,则∠A的度数为________.
⑺、平面内有线段AB和直线l,点A、B到直线l的距离分别是4㎝和6㎝,则线段AB的中点P到直线l的距离是________.
(8)、如图:直角ΔABC中,∠C=90°,AC=3,BC=4,若以C为圆心,R为半径所作的圆与斜边AB只有一个公共点,则R的取值范围是______________.
八、注意数学思想在解题中的应用
1、方程思想
己知如图,在ΔABC中,∠C=90°,D在BC上, BD=6,AD=BC,cos∠ADC=,则DC的长为_____.
2、函数思想
(1)如图,正方形ABCD的边长为4㎝,A是BC上不与B、C重合的任意一点,连接AP,过点P作PQ⊥AP交DC于Q,设BP的长为x㎝,CQ的长为y㎝,
①求点P在BC上运动的过程中, y的最大值;
②当y=㎝时,求x的值.
(2)有一块直角三角形的木板,∠C=90°,AB=5, BC=3,将它加工成一个面积最大的正方形木板,设计一种方案,并求出这个正方形木板的边长.
3、分类思想
己知关于x的函数的图象与x轴有交点,求a的取值范围.
4、化归思想
如图:在梯形ABCD中,AD∥BC,AB=CD,对角线AC、BD相交于点O,且AC⊥BD,AD=3, BC=5,求AC的长.
5、数形结合思想
(1)已知:点A(-1,-1)在抛物线y=(k2-1)x2-2(k-2)x+1上
①求抛物线的对称轴
②若B与A关于抛物线的对称轴对称,问是否存在与抛物线只交于一点B的直线?如果存在,求符合条件的直线?如果不存在,说明理由.
(2)如图①,⊙O的弦CD垂直于直径AB,垂足为点G,点E在弧CB上,作直线CE、ED与直线AB分别交于点F、M,连接OC,求证:OC2=OM·OF
如图②,把①中的“点E在弧CB上”改为“E在弧AD上”其余条件不变(如图),试问①中的结论是否成立?并说明理由.
九、认真复查
复查是交卷之前的最后一道工序,认真进行复查,能有效提高考试成绩.
首先应当纠正笔误,大家都有体验:有时我们做题时心里想的是某一内容,而同时笔下写的却是另一内容,这就是笔误.这种情况特别是几何论证中出现的较多,有时错写一个字母,自己还不知道,但对解题却影响极大,清除笔误一般只要认真核查一遍就行了.
其次要纠正算误,一道题,我们的思路方法都是对的,只是具体数据的计算上出了错,这种纯计算上的失误导致丢分甚为可惜,因为这道题从根本上讲你是会做的,应该拿满分,纠正算误的方法不仅仅是重算一次,如果可能,争取换一种方式算,有经验的会计师会横累计、竖累计,为什么不照原来的算法再重算一次呢?因为如果你第一次在某处犯了错误,第二次在该处很可能再犯同样的错误(一个人要想在极短的时间内,在相同的条件下发现刚刚犯过的错误是很难的),换一种方式算就可以避免了.
另外,还要注意运用所学知识去检验,比如+、-、×、÷、乘方、开方可以互相验算,因式分解可以用多项式的乘法验算,解方程(组)可以把结果代入原方程或方程组中去验算,几何题可以考察推理是否恰当,理由是否充足等等.
最后,还要仔细复查全卷,中考是规定时间内的竞争,复查时应重新审题,多角度、多思路考虑,如确定需要改,又经过深思熟虑后,才能擦去原题答案,以免失去得分机会.方法有:a.观察估计法;b.特例检查法;c.简单化检查法;d.数形直观法;e.逻辑检查法;f.发散性检查法等.这样既拿小分,又争大分,就有希望得满分.对比较隐蔽的错误,或是把握不大的答案,则要作综合分析.
十、了解评分标准
也许你没有写清所设未知数x的意义,扣1分.
也许你没有检验,扣1分.
如果没有最后的“答”这一步,再扣1分.
有的同学在解方程这一步就把不合题意的x2=-3去掉了,只写出原方程的一个解x=10,也要扣分.你看看,本来可以稳拿5分的题,结果只能得到2分,其它类型的题目也都存在类似的问题,应当按照标准的格式,认真写清每一个必要的步骤,千万不能随意省略关键性的步骤.
此外,不按要求答题,答案不写在指定位置,该带单位而不带单位或带错单位的也要扣分,作图题不保留作图痕迹,卷面不整洁等,都会导致丢冤枉分,考前了解评分标准,以避免不必要的失分.有时一分甚至半分之差,就会使你的结局由“重点”变为“普通”或由“计内”变为“择校”,说“一分值千金”丝毫也不夸张.
预祝同学们中考心想事成!万事如意!敬请各位同仁、同学们提出宝贵意见.
同课章节目录
