2021小升初数学专题复习第四-五讲平面图形的特征及计算教师版+学生版
文档属性
| 名称 | 2021小升初数学专题复习第四-五讲平面图形的特征及计算教师版+学生版 |

|
|
| 格式 | docx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-31 00:00:00 | ||
图片预览



文档简介
2021
专题讲解+配套练习
小升初数学专题复习
小升初
第四-五讲 平面图形的特征及计算-教师版
三角形
一、知识梳理
由三条线段围成的图形(每相邻两条线段的端点相连)叫做三角形。
(1)特征
三角形都有三条边、三个顶点、三个角;
三角形内角和是180度。
从三角形的一个顶点到它的对边做一条垂线,顶点和垂足之间的线段叫三角形的高,这条对边叫做三角形的底。三角形有三条高。
三角形具有稳定性。
(2)计算公式
三角形面积:三角形面积=底×高÷2
用字母表示:
s=ah/2
(3) 分类
按角分
锐角三角形 :三个角都是锐角。
直角三角形 :有一个角是直角。等腰三角形的两个锐角各为45度,它有一条对称轴。
钝角三角形:有一个角是钝角。
按边分
不等边三角形:三条边长度不相等。
等腰三角形:有两条边长度相等;两个底角相等;有一条对称轴。
等边三角形:三条边长度都相等;三个内角都是60度;有三条对称轴。
二、例题精讲
例1:求下列三角形的面积。(单位m)
15
12
15
15
12
10
解析:直接带入三角形的面积公式:s=ah/2
解1:s=10×12÷2=120÷2=60
2:s=15×15÷2=225÷2=112.5
3:s=12×15÷2=180÷2=90
总结:计算三角形面积的时候,找准底和高,直接带入公式。
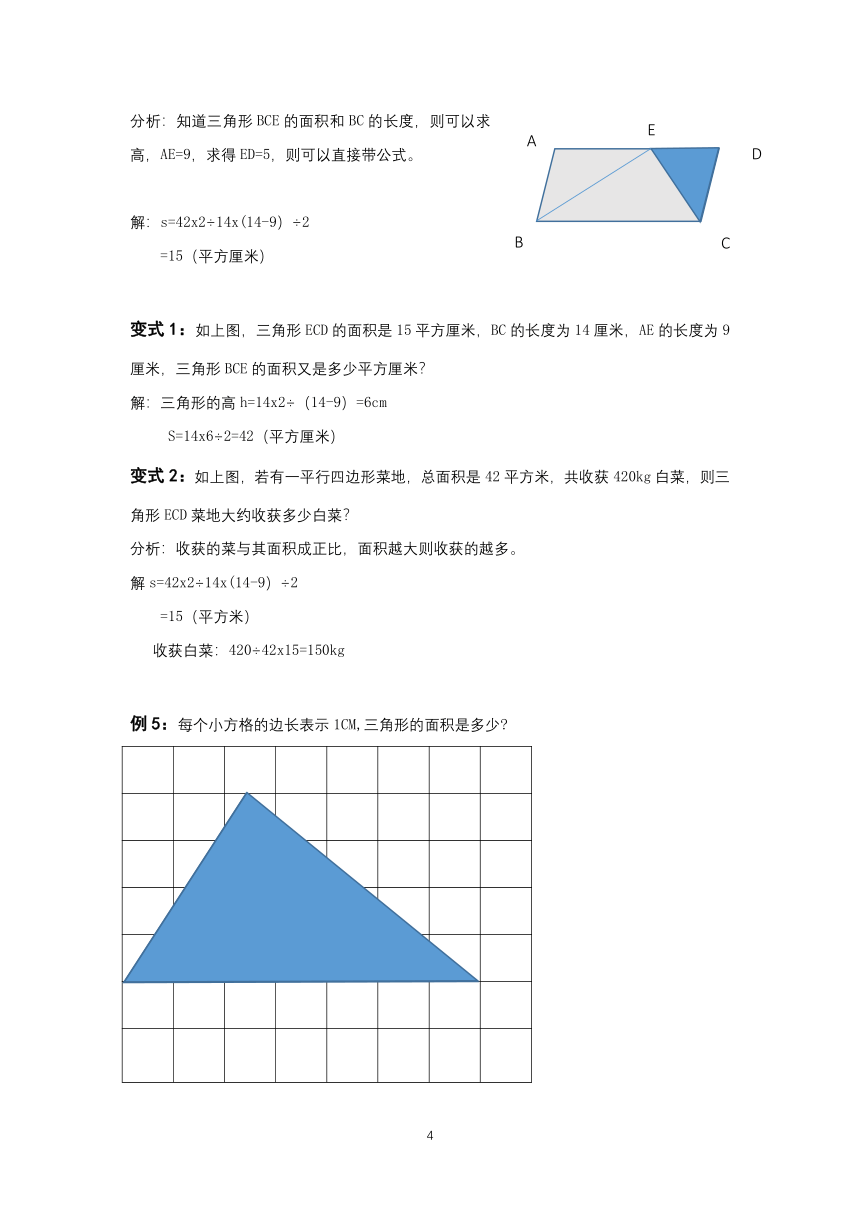
变式1:如图:求三角形的面积:
分析:本题要找准三角形的高是谁,底是谁,要知道底和高的垂直关系则可以找到底是4cm,高是3cm。带入公式
解:s=ah÷2=3×4÷2=6
变式2:已知等腰三角形的底边上的高是8cm,底边是高的1.5倍,求三角形的面积。
解:s=ah÷2=8×8×1.5÷2=48
8
6
例2:把大、小两个正方形拼在一起,它们的边长分别是8米和6米,那么图中阴影部分的面积是多少平方米?
分析:本题首先要找准底和高。然后直接带公式。
解:s=ah/2=(8-6)×6÷2=6
变式1:如图,求图中阴影部分的面积是多少平方米?
10
7
解:s=ah/2=(10-7)×7÷2=10.5
变式2:如图:求图中阴影部分的面积是多少平方米?
6
8
解:s=ah/2=6×6÷2=18
例3:如图,平行四边形ABCD的面积是32平方厘米,三角形CED是一个直角三角形,已知AE=5厘米,CE=4厘米,那么阴影部分的面积是多少平方厘米?E
A
B
C
D
分析:可以把平行四边形分成一个矩形和2个相等的三角形,用总面积减去矩形的面积除以2即可:
解:s=(32-5×4)÷2
=12÷2
=6(平方厘米)
变式1:如上图:若四边形ABCE的面积是26平方厘米,AE=5厘米,CE=4厘米,那么阴影部分的面积是多少平方厘米?
解:s=26-5×4
=26-20
=6(平方厘米)
变式2:在上题中,已知平行四边形ABCD的面积是32平方厘米,无其余条件,则阴影三角形的面积最大是多少?
解:S=32÷2=16(平方厘米)
例4:如图,在平行四边形ABCD中,三角形BCE的面积是42平方厘米,BC的长度为14厘米,AE的长度为9厘米,三角形ECD的面积又是多少平方厘米?
A
B
C
D
E
分析:知道三角形BCE的面积和BC的长度,则可以求高,AE=9,求得ED=5,则可以直接带公式。
解:s=42x2÷14x(14-9)÷2
=15(平方厘米)
变式1:如上图,三角形ECD的面积是15平方厘米,BC的长度为14厘米,AE的长度为9厘米,三角形BCE的面积又是多少平方厘米?
解:三角形的高h=14x2÷(14-9)=6cm
S=14x6÷2=42(平方厘米)
变式2:如上图,若有一平行四边形菜地,总面积是42平方米,共收获420kg白菜,则三角形ECD菜地大约收获多少白菜?
分析:收获的菜与其面积成正比,面积越大则收获的越多。
解s=42x2÷14x(14-9)÷2
=15(平方米)
收获白菜:420÷42x15=150kg
例5:每个小方格的边长表示1CM,三角形的面积是多少?
分析:由图可以看出,三角形的底边是7,高是4带入公式
S=7×4÷2=14(平方厘米)
变式1:如下图,每个小方格的边长表示1CM,三角形的面积是多少?
解:s=2×3÷2=3(平方厘米)
变式2:如下图,每相邻三个点所形成的三角形都是面积为1的等边三角形,计算△ABC的面积.
分析 这是个三角形,虽然有三角形面积公式可用,但判断它的底和高却十分困难,只能另想别的办法:这个三角形是处在长是6、宽是4的矩形内,除此之外还有其他三个直角三角形,如下图(b),这三个直角三角形面积很容易求出,再用矩形面积减去这三个直角三角形面积,就是所要求的三角形面积.
解:矩形面积是6×4=24.
直角三角形I的面积是:
6×2÷2=6.
直角三角形Ⅱ的面积是:4×2÷2=4,
直角三角形Ⅲ的面积是:4×2÷2=4.
所求三角形的面积是:
24-(6+4+4)=10
三、课堂总结
找准三角形的各边,牢记公式,灵活运用上解决三角形问题的关键和方法。
课后作业
1.比一比下面两个图形的面积。结果是( )。
① ② A.①>②
B. ①<②
C. ①=②
答案C
2.若图中涂色部分代表240元,则全部代表多少钱?
分析,可以算出一个小三角形代表多少,则可以算出全部
解:240÷4×9=540元
3.如图ABFE和CDEF都是长方形,AB的长是4厘米,BC的长是3厘米,那么图中阴影部分的面积是多少平方厘米?
分析:根据三角形等底等高的性质,可以得出阴影部分的面积和空白一样。
解:s=4×3÷2=6(平方厘米)
4.一块正方形菜地,边长20m,平均分成两块三角形菜地,其中一块种白菜,另一块种菠菜,已知每平方米可以收获白菜10kg,菠菜6kg,问这块地收获白菜菠菜个多少千克?
解:三角形的面积s=20×20÷2=200(平方米)
收获白菜:200x10=2000kg
收获菠菜:200x6=1200kg
5.已知三角形ABC的面积为1,BE=2AB,BC=CD,求三角形BDE的面积?(下页图)
分析,见右图,连结CE.对于三角形ABC与三角形BEC,分别把AB和BE可知,S△BEC=2S△ABC=2.显然,三角形BEC和三角形CED是两个等底(BC=CD)、等高的三角形,因此 S△CED=S△BEC=2。 这样,S△BDE=S△BEC+S△CED=4。
长方形
一、知识梳理
四个角都是直角的平行四边形叫做长方形
(1)特征
长方形有四条边,对边相等,4个角都是直角的四边形。
长方形长边的长叫作长,短边的长叫宽。
长方形是轴对称图形,它有两条对称轴。
(2)计算公式
周长=(长+宽)×2
字母表示为:
c=2(a+b)
面积=长×宽
字母表示为:
s=ab
二、例题精讲
例1:求长方形的周长和面积
35cm
20cm
5dm
12dm
分析:对于单一的题目,直接带公式:
c=(35+20)×2=55x2=110cm s=35x20=700
30厘米
21厘米
C=(5+12)x2=17x2=34dm s=5x12=60
例2:一张长方形的A4纸(如下图),它的面积是多少
平方厘米?
30×21=630(平方厘米)
变式1:如果从这张纸上剪下一个最大的正方形,
这个正方形的面积是多少?
21×21=441(平方厘米)
变式2:如果从这张纸上剪下一个最大的正方形,剩下的面积是多少?
630-441=169(平方厘米)
例3:小红用一根长 8 厘米的铁丝,围成一个最大的正方形,这个正方形的边长是多少?面积是多少?
分析,要正方形最大,则48即周长,根据公式计算边长,然后计算面积。
解:8÷4=2厘米
2×2=4平方厘米
变式1:小红用一根长铁丝围成一个正方形,这个正方形的面积是16平方厘米。它的周长是多少?边长是多少?
解:16=4×4,所以边长是4厘米
C=4×4=16厘米
变式2:小红用n个长3厘米,宽x厘米的长方形拼车一个正方形,正方形的周长12厘米,求整数x和n?
解:12÷4=3 所以边长为3,长大于宽,所以x=1或者x=2
1)若x=1,则n=3
2)若x=2,则n=2
花圃
例4:小区前面有一块60米边长的正方形空坪,现要在空坪的中间做一个长32米、宽28米的长方形花圃,其余的植上草皮.(如下图)
花圃的面积是多少平方米?草皮的面积是多少平方米?
解:花圃:32×28=896平方米
草皮:60×60-896=2704平方米
变式1:小区前面有一块长60米,宽40米的长方形草地,现在修一条平行于长的长方形小路,宽2m,问草地面积还有多少?
解:
S=(40-2)×60=2280平方米
变式2:小区前面有一块长60米,宽40米的长方形草地,现在修两条分别平行于长和宽的长方形小路,小路宽2m,问草地面积还有多少?
解:
S=(60-2)×(40-2)=2204平方米
例5:一块广告牌长6米,宽2米,如果每平方米用油漆2千克,这块广告牌一共要用多少千克油漆?
分析:知道每平方米用油漆2千克,只要算出有多少面积即可
解:S=6×2=12平方米
12×2=24千克
变式1:一间长方形会议室长12米,宽6米。这个会议室地板面积是多少平方米?合多少平方分米?如果一块地砖的面积是9平方分米,铺完这间会议室地板至少要用多少块这样的地砖?
解:12×6=72平方米=7200平方分米
7200÷9=800块
变式2:一间长方形会议室长12米,宽6米。这个会议室地板面积是多少平方米?合多少平方分米?如果一块正方形地砖的边长是3分米,铺完这间会议室地板至少要用多少块这样的地砖?
解:12×6=72平方米=7200平方分米
36×3=9平方分米
7200÷9=800块
三、课堂总结
在解决长方形问题的时候要抓住其特征进行条件查找,在记住公式的同时灵活运用在解题上面。
四、课后作业
一块长方形菜地,长20米,宽8米。如果要给这块菜地围上篱笆,篱笆的长是多少米?
答案:(20+8)×2=56m
9
4
5
5
7
2
2.计算下面图形的面积。
9×4=36(平方厘米) 5×5=25(平方厘米)
有一个长方形田地。长是600米,宽是300米,面积是多少公顷?如果围上篱笆,篱笆的长是多少米?如果每公顷收白菜150吨,可以收白菜多少吨?
答案:s=600×300=180000平方米=18公顷
C=(600+300)×2=1800米
18×150=2700吨
4.一个零件形状如图,计算它的周长和面积。(单位:厘米)
6
14
14
6
答案:整体看
s=14×14-6×6=108平方厘米
C=14×4=56厘米
5.一洒水车,每分钟行驶200米,洒水的宽度是10米,洒水车行驶6分钟,能给多大的地面洒上水?
答案:6×200×10=12000平方米
正方形
一、知识梳理
长和宽相等的长方形是正方形。
(1)特征:
四条边都相等,四个角都是直角的四边形。
正方形每条边的长叫作边长。
正方形是轴对称图形,它有4条对称轴。正方形还是中心对称图形。
(2)计算公式
周长=边长x4
用字母表示:
c=4a
面积=边长x边长
用字母表示:
s=a × a=
二、例题精讲
例1:
边长:16米 边长:300厘米
面积:16×16=256平方米 面积:300×300=90000平方厘米
周长:16×4=64米 周长:300×4=1200厘米
例2:把一个长10厘米,宽3厘米的长方形硬纸剪成面积尽可能大的正方形,可以剪( )。
A.1个 B.2个 C.3个
分析,长方形的长是宽的3倍还多1,所以可以剪3个
选C
变式1:5个边长1m的正方形拼在一起构成一个长方形,周长是多少?
C=(5+1)×2=12m
变式2: 用6个边长1m的正方形拼在一起构成一个长方形,周长是多少?
分析:6个正方形可以分2排或者1排,所以有两种情况
c=(6+1)×2=14m
C=(2+3)×2=10m
例3:用边长1厘米的小正方形拼成图形 ,它的周长是( ),面积是( )。
分析:图形可以通过移动边使其变成一个长方形c=(2+3)×2=10。面积没有变化
答案:10厘米,4平方厘米
变式1:用边长1厘米的小正方形拼成图形,它的周长是( ),面积是( )。
C=(2+5)×2-1=13厘米
S=5+2=7平方厘米
变式2:用边长1厘米的小正方形拼成图形,它的周长是( ),面积是( )。
解:
C=(3+5)×2=16厘米
S=3+3+5=11平方厘米
例4:小明家的客厅长5米,宽4米。地面上铺有边长为5分米的正方形地砖。铺这个客厅,需要多少块地砖?
分析:先换算单位,根据面积相等计算
解:5米=50分米 4米=40分米
50×40÷(5×5)
=2000÷25
=80(块)
变式1:小明家的客厅长5米,宽4米。地面上铺有边长为5分米的正方形地砖,这种地砖20元一块。铺这个客厅,需要多少块地砖?买这些地砖共需多少钱?
由上题可以知道需要80块
解:
总钱=80×20=1600元
变式2:小明家的客厅长5米,宽4米。地面上铺有边长为5分米的正方形地砖,铺这个客厅,买这些地砖共需1600元。这种地砖多少元一块?
计算单价,有总价除以块数
解:
1600÷80=20元
例5:小红用一根长 48 厘米的铁丝,围成一个最大的正方形,这个正方形的边长是多少?面积是多少?
分析,要正方形最大,则48即周长,根据公式计算边长,然后计算面积。
解:48÷4=12厘米
12×12=144平方厘米
变式1:小红用一根长铁丝围成一个正方形,这个正方形的面积是144平方厘米。它的周长是多少?边长是多少?
解:144=12×12,所以边长是12厘米
C=12×4=48厘米
变式2:小红用3个长3厘米,宽2厘米的长方形拼车一个正方形,求正方形的周长和面积?
解:c=3×4=12厘米
S=3×2×3=18平方厘米
三、课堂总结
解决正方形问题的时候要抓住其特征进行条件查找,灵活运用。
四、课后作业
1.求下面长方形的周长和面积:(单位:厘米)
5 4
1
周长:12厘米 周长:16厘米
面积: 5平方厘米 面积:16平方厘米
6
6
6×6=36(平方厘)米)
9×2=18(平方厘)米)
9
2
7
8×7=56(平方厘米)
2.求下图的面积
3.用18个边长为1厘米的小正方形拼成一个长方形,要使长方形的周长最大应怎样拼?周长最小呢?请画出图,并列式计算。
解
要是周长最大,则需要一字排开
C=(1+18)×2=38cm
要是周长最小,则需要尽可能的靠拢:如图
C=(3+6)×2=18cm
4.足球场是一个长方形,长 100 米,宽 75 米,小明沿着足球场跑了 2 圈,跑了多少米?
解:c=(100+75)×2=350m
一块长方形菜地,长6米,宽4米。四周围上篱笆,篱笆长多少米?如果一面靠墙,篱笆至少要多少米?
答案:20m,14m
平行四边形
一、知识梳理
有两组对边分别平行的四边形是平行四边形。
(1) 特征
相对的边平行且相等。对角相等,相邻的两个角的度数之和为180度。平行四边形容易变形。
(2) 计算公式
平行四边形的面积=底×高
用字母表示:
s=ah
二、例题精讲
例1:右图中有( )个平行四边形,
答案:3
变式1:下图中有( )个平行四边形
答案:9
变式2:下图中有( )个平行四边形
答案:13
例2:计算下面各个平行四边的面积。(单位:m)
S1=2.8×1.2=3.36平方米
S2=1.6×0.8=1.28平方米
例3: 一平行四边形的底27厘米,高12.5厘米;另一条底18厘米,这条底边上的高是多少厘米?
分析,根据面积相等即可求得。
27×12.5=337.5(厘米2)
337.5÷18=18.75(厘米)
答:这条底边上的高是18.75厘米。
变式1:一平行四边形的底24厘米,高是底的一半;另一条底18厘米,这条底边上的高是多少厘米?
24×24÷2÷18=16厘米
变式2:一平行四边形的面积是18平方厘米,高是底的一半;另一条底是前一条底的一半,另一条底边上的高是多少厘米?
18÷2=9 9=3×3
所以,底是3厘米,高6厘米
6×2=12厘米
答:另一条底边上的高是12厘米.
例4:把一个长方形拉成平行四边形后,它的面积( )
A比原来大 C比原来小
B与原来相等 D无法确定
分析,长方形边长平行四边形后,高变小,所以选C
变式1:把一个平行四边形拉成长方形后,它的面积( )
A比原来大 C比原来小
B与原来相等 D无法确定
分析,长方形边长平行四边形后,高变小,反之选A
变式2:把一个长方形拉成平行四边形后,它的面积变成原来的一半,则高怎么变化
答:高变为原来的一半
例5:如图,两个边长10厘米的正方形相互错开3厘米,那么图中阴影平行四边形的面积是多少?
分析:阴影部分的面积等于总面积减去四个小三角形的面积。
S=10×10×2-10×10-3×3
=91平方厘米
变式1:上题中,当正方形错开5厘米时,阴影面积是多少?
S=10×10×2-10×10-5×5
=75平方厘米
变式2:上题中,当正方形大约错开多少厘米时,阴影面积是总面积的四分之一?
由题意得:50=10×10×2-10×10-n×n
n≈7cm
课堂总结
图形面积的计算属于较简单的问题,找准数量关系是解题的关键。
四、课后作业
1.已知下图中正方形的周长是36厘米,求平行四边形的面积。
36÷4=9(厘米)
9×9=81(平方厘米)
2.平行四边形的面积是36.8平方分米,高是2.3分米,底是多少?
a = s÷h
= 36.8÷2.3
= 16(分米)
答:底是16分米。
3.一块平行四边形的菜地,底是30米,高是21米。如果每棵大白菜占地9平方分米,这块地一共可种多少棵大白菜?
30×21=630(平方米)
630平方米=63000平方分米
63000÷9=7000(棵)
答:这块地一共可种7000棵大白菜。
4.一块平行四边形的铁皮的周长是82厘米,一条底长是16厘米,这条底上的高是20厘米,求另一条底上的高是多少厘米?
82÷2-16=25(厘米)
16×20÷25=12.8(厘米)
5.如右图,四边形ABCD和DEFG都是平行四边形,证明它们的面积相等
证明:连结CE,平行四边形ABCD的面积等于△CDE面积的2倍,而平行四边形DEFG的面积也是△CDE面积的2倍。
∴平行四边形ABCD的面积与平行四边形DEFG的面积相等。
梯形
一、知识梳理
梯形:指一组对边平行而另一组对边不平行的四边形叫做梯形。
上底
①上底、下底:平行的两边叫做梯形的底边,其中长边叫下底,短边叫上底;
高
②腰:不平行的两边叫腰;
③高:夹在两底之间的垂线段叫梯形的高。
下底
(1)特征
只有一组对边平行的四边形。
中位线等于上下底和的一半。
两腰相等的梯形是等腰梯形,等腰梯形有一条对称轴。
(2) 公式
梯形的面积:(上底+下底)×高÷2
用字母表示:
s=(a+b)h/2
二、例题精讲
20
32
20
例1:计算下面各梯形的面积。(单位:厘米)X k
分析:直接带入公式
解:
(15+20)×8÷2 =140(平方厘米)
(20+32)×20÷2 =520(平方厘米)
例2:有一块梯形花地,上底是8米,下底是10米,高是4.8米。已知每株花占地0.06平方米,这块地能种花多少株?
分析:先计算面积,然后计算株数。
解:(8+10)×4.8÷2÷0.06=720(株)
变式1:有一块梯形花地,上底是8米,下底是10米,高是4.8米。已知,这块地能种花720株,每株花占地多少平方米?
解:(8+10)×4.8÷2÷720=0.06(平方米)
变式2:有一块梯形花地,上底是8米,下底是10米。已知,这块地能种花720株且每株花占地0.06平方米,问高是多少米?
解:设高是h:
(8+10)×h÷2÷720=0.06
解得h=4.8m
例3:一个梯形的上底是12分米,高是8分米,面积是108平方分米。这个梯形的下底是多上分米?
分析:根据面积公式求解。
解:108×2÷8-12=15(分米)
变式1:一个梯形的上底是12分米,下底是15分米,面积是108平方分米。这个梯形的高是多少分米?
解:h=108×2÷(12+15)
=8dm
变式2:一个梯形的上底是12分米,下底是上底的2倍,面积是108平方分米。这个梯形的高是多少分米?
解:h=108×2÷(12+12×2)
=6dm
例4:已知梯形的面积是20平方分米,求阴影部分的面积。
3.2分米
解:20×2÷(3.2+6.8)=4(分米)
变式1:如图所示,大正方形的边长是12米,小正方形的边长是5米,求阴影部分的面积。
w W w . x K b 1.c o M
解:(5+12)×12÷2=102(平方米)
变式2:图中,阴影部分的面积是13.5平方厘米,着个梯形的面积是多少?
7厘米
解:13.5×2÷9=3(厘米)
(7+9)×3÷2=24(平方厘米)
例5:用篱笆围城一个梯形养鸡场,一边利用房屋的墙壁,篱笆的 长是65米,求养鸡长得面积。
X k B 1 . c o m
15米
解:(65-15)×15÷2=375(平方米)
变式1:上题中,若上底是下底的3倍,则上底是多少?
(65-15)÷(1+3)=10m
变式2:如下图,若梯形上底是下底的3倍,面积是300平方米,则高是多少?
15米
解:h=300×2÷(15+15×3)
=10m
课堂总结
牢记梯形的面积公式。熟练运用。
四、课后作业
1、可以把一个梯形分成两个( )形,也可以分成一个( )形和一个( )形。
2、梯形的上底长8厘米,下底长14厘米,高是上底的一半。梯形的面积是( )平方厘米。
3、两个完全一样的梯形拼成的一个平行四边形的面积是80平方厘米,高是5厘米,梯形的上底是7厘米,梯形的下底是( )厘米。
4、一个梯形上下底的和是16米,高是7米,它的面积是( )
5、判断下列各题,对的打√,错的打×
(1)两个面积一样的梯形一定可以拼成一个平行四边形 ( )
(2)平行四边形的面积是梯形面积的两倍( )
(3)计算一个梯形的面积,比武知道他的上下底和高 ( )
(4)一个梯形两底的和是12米,高是10米,则它的面积是60平方米 ( )
答案:1.三角形, 三角形, 平行四边形 2. 44 3. 9 4. 56 5.××√√
5.如图,梯形ABCD的面积是45平方米,高6米,△AED的面积是5平方米,BC=10米,求阴影部分面积.
解:∵梯形面积=(上底+下底)×高÷2
即45=(AD+BC)×6÷2,
45=(AD+10)×6÷2,
∴AD=45×2÷6-10=5米。
∴△ADE的高是2米。
△EBC的高等于梯形的高减去△ADE的高,
即6-2=4米,
S=BC×4÷2=20平方米
圆
一、知识梳理
(1)圆
到定点的距离等于定长的所有点组成的图形。
圆中心的一点叫做圆心。一般用字母o表示。
半径:连接圆心和圆上任意一点的线段叫做半径。一般用r表示。
在同一个圆里,有无数条半径,每条半径的长度都相等。
通过圆心并且两端都在圆上的线段叫做直径。一般用d表示。
同一个圆里有无数条直径,所有的直径都相等。
同一个圆里,直径等于两个半径的长度,即d=2r。
圆的大小由半径决定。 圆有无数条对称轴。
(2)圆的画法
把圆规的两脚分开,定好两脚间的距离(即半径);
把有针尖的一只脚固定在一点(即圆心)上;
把装有铅笔尖的一只脚旋转一周,就画出一个圆。
(3) 圆的周长
围成圆的曲线的长叫做圆的周长。
把圆的周长和直径的比值叫做圆周率。用字母∏表示。
(4) 圆的面积
圆所占平面的大小叫做圆的面积。
(5)计算公式
d=2r
r=d/2
c=∏d
c=2∏r
s=∏r?
二、例题精讲
例1:求下列圆的周长及面积。
(半径3) (直径12)
周长:2×3.14×3=18.84 周长:3.14×12=37.68
面积:3.14×3×3=28.26面积:3.14×(12÷2)×(12÷2)=113.04
例2:圆形草坪的半径是10m,每平方米草皮8元,铺满需要多少钱?
分析:先求出面积,即可求得钱数。
解3.14×10×10=314平方米
314×8=2512元
变式1:圆形草坪的直径是20m,每平方米草皮8元,铺满需要多少钱?
解:20÷2=10米
3.14×10×10=314平方米
314×8=2512元
变式2:圆形草坪的直径是20m,铺满需要钱2512元,每平方米草皮多少元?
解:20÷2=10米
3.14×10×10=314平方米
2512÷314=8元
例3:光盘的银色部分是一个圆环,内圆半径是2cm,外圆半径是6cm。内圆的面积是多少?
分析:直接带公式
解:S=3.14×2?
变式1:光盘的银色部分是一个圆环,内圆半径是2cm,外圆半径是6cm。外圆的面积是多少?
解:s=3.14×6?
变式2:光盘的银色部分是一个圆环,内圆半径是2cm,外圆半径是6cm。圆环的面积是多少?
解:方法一: 3.14×6?-3.14×2?
=113.04-12.56
=100.48(cm?)
方法二:3.14×(6?-2?)
=3.14×32
=100.48(cm?)
例4:公园里有一棵大树,同学们用一根20米长的绳子围绕这棵树绕了6圈,还剩下1.16米,求树干的直径是多少?
分析:6圈其实就是树周长的6倍,由此建立等式:
解:(20-1.16)÷6÷3.14
=1m
变式1:公园里有一棵大树,同学们用一根20米长的绳子围绕这棵树绕了几圈,还剩下1.16米,树干的直径是1m,求大家绕了多少圈?
解:(20-1.16)÷1÷3.14
=6圈
变式2:公园里有一棵大树,同学们用一根长的绳子围绕这棵树绕了6圈,还剩下1.16米,树干的直径是1m,求绳子有多少米?
解:3.14×1×6+1.16=20米
例5:一个运动场如右图所示,两端是半圆形,中间是长方形。
小海在运动场上跑2圈,一共跑了多少米?
分析:操场周长可以看成一个圆周加上一个长方形的两个长。
解:L=(100+100+3.14×60)×2
=388.4×2
=776.8m
变式1:一个运动场如右图所示,两端是半圆形,中间是长方形。小海在运动场上跑了776.8米,一共跑了多少圈?
解:(776.8÷2-200)÷3.14÷60=2圈
变式2:一个运动场如右图所示,两端是半圆形,中间是长方形。小海和小明在运动场上同向而跑,6分钟时,小海跑2圈而小明跑了2圈半,问他们的速度差?
解:L1=(100+100+3.14×60)×2
=388.4×2
=776.8m
L2=(100+100+3.14×60)×2.5
=388.4×2.5
=971m
小海的速度:776.8÷6=129.47m/min
小明的速度:971÷6=161.83m/min
速度差:161.83-129.47=32.36m/min
课堂总结
在圆一个小节,要注意审题,看清楚是直径还是半径,牢记公式,认真书写。
四、课后作业
1. 一个圆形茶几桌面的直径是1m,它的面积是多少平方米?
1÷2=0.5(m)
3.14×0.5?=0.785(m?)
答:它的面积是0.785m?。先求出半径,再求圆的面积。
2. 一个圆形环岛的直径是50m,中间是一个直径为10m的圆形花坛,其他地方是草坪。草坪的占地面积是多少?
3.14×(25?-5?)
=3.14×600
=1884(m?)
要求草坪的占地面积,也就是求圆环的面积。
3.看图求出阴影部分的面积。(单位:厘米)
10
15
6
6
解:
s=6×6-3.14×6×6÷4=7.74平方厘米
S=3.14×15×15-3.14×10×10=392.5平方厘米
4.为美化校园,学校在教学楼前修了一个周长是31.4m的圆形花坛,围绕花坛铺了一条2m宽的环形小路。这条小路的面积是多少平方米?
解:31.4÷3.14÷2=5m
S=3.14×(5+2)×(5+2)-3.14×5×5=75.36平方米
5.一个圆和一个正方形,它们的周长相等,它们的面积相比较是( )。
A.圆的面积大 B.正方形的面积大 C. 面积同样大
6.如果两个圆的半径之比是2:3,那么这两个圆的面积之比是( )
A.2:3 B.3:2 C.4:9
7.车轮滚动一周,求所行驶的路程就是求车轮的( )。
A.直径 B.周长 C. 面积
答案:ACB
附:
单位换算
熟记基本换算关系: 高级单位化低级单位:×进率 低级单位聚高级单位:÷进率
(长度单位):1千米=1000米????1米=10分米 1分米=10厘米
1厘米=10毫米 1米=100厘米??? ?? 1米=1000毫米
(面积单位):1平方千米=100公顷 1公顷=10000平方米
1平方米=100平方分米 1平方分米=100平方厘米
1平方厘米=100平方毫米
第四-五讲 平面图形的特征及计算-学生版
三角形
一、知识梳理
由三条线段围成的图形(每相邻两条线段的端点相连)叫做三角形。
(1)特征
三角形都有三条边、三个顶点、三个角;
三角形内角和是180度。
从三角形的一个顶点到它的对边做一条垂线,顶点和垂足之间的线段叫三角形的高,这条对边叫做三角形的底。三角形有三条高。
三角形具有稳定性。
(2)计算公式
三角形面积:三角形面积=底×高÷2
用字母表示:
s=ah/2
(3) 分类
按角分
锐角三角形 :三个角都是锐角。
直角三角形 :有一个角是直角。等腰三角形的两个锐角各为45度,它有一条对称轴。
钝角三角形:有一个角是钝角。
按边分
不等边三角形:三条边长度不相等。
等腰三角形:有两条边长度相等;两个底角相等;有一条对称轴。
等边三角形:三条边长度都相等;三个内角都是60度;有三条对称轴。
二、例题精讲
例1:求下列三角形的面积。(单位m)
15
12
15
15
12
10
解析:直接带入三角形的面积公式:s=ah/2
解1:s=10×12÷2=120÷2=60
2:s=15×15÷2=225÷2=112.5
3:s=12×15÷2=180÷2=90
总结:计算三角形面积的时候,找准底和高,直接带入公式。
变式1:如图:求三角形的面积:
分析:本题要找准三角形的高是谁,底是谁,要知道底和高的垂直关系则可以找到底是4cm,高是3cm。带入公式
解:s=ah÷2=3×4÷2=6
变式2:已知等腰三角形的底边上的高是8cm,底边是高的1.5倍,求三角形的面积。
解:s=ah÷2=8×8×1.5÷2=48
8
6
例2:把大、小两个正方形拼在一起,它们的边长分别是8米和6米,那么图中阴影部分的面积是多少平方米?
分析:本题首先要找准底和高。然后直接带公式。
解:s=ah/2=(8-6)×6÷2=6
变式1:如图,求图中阴影部分的面积是多少平方米?
10
7
解:s=ah/2=(10-7)×7÷2=10.5
变式2:如图:求图中阴影部分的面积是多少平方米?
6
8
解:s=ah/2=6×6÷2=18
例3:如图,平行四边形ABCD的面积是32平方厘米,三角形CED是一个直角三角形,已知AE=5厘米,CE=4厘米,那么阴影部分的面积是多少平方厘米?E
A
B
C
D
分析:可以把平行四边形分成一个矩形和2个相等的三角形,用总面积减去矩形的面积除以2即可:
解:s=(32-5×4)÷2
=12÷2
=6(平方厘米)
变式1:如上图:若四边形ABCE的面积是26平方厘米,AE=5厘米,CE=4厘米,那么阴影部分的面积是多少平方厘米?
解:s=26-5×4
=26-20
=6(平方厘米)
变式2:在上题中,已知平行四边形ABCD的面积是32平方厘米,无其余条件,则阴影三角形的面积最大是多少?
解:S=32÷2=16(平方厘米)
例4:如图,在平行四边形ABCD中,三角形BCE的面积是42平方厘米,BC的长度为14厘米,AE的长度为9厘米,三角形ECD的面积又是多少平方厘米?
A
B
C
D
E
分析:知道三角形BCE的面积和BC的长度,则可以求高,AE=9,求得ED=5,则可以直接带公式。
解:s=42x2÷14x(14-9)÷2
=15(平方厘米)
变式1:如上图,三角形ECD的面积是15平方厘米,BC的长度为14厘米,AE的长度为9厘米,三角形BCE的面积又是多少平方厘米?
解:三角形的高h=14x2÷(14-9)=6cm
S=14x6÷2=42(平方厘米)
变式2:如上图,若有一平行四边形菜地,总面积是42平方米,共收获420kg白菜,则三角形ECD菜地大约收获多少白菜?
分析:收获的菜与其面积成正比,面积越大则收获的越多。
解s=42x2÷14x(14-9)÷2
=15(平方米)
收获白菜:420÷42x15=150kg
例5:每个小方格的边长表示1CM,三角形的面积是多少?
分析:由图可以看出,三角形的底边是7,高是4带入公式
S=7×4÷2=14(平方厘米)
变式1:如下图,每个小方格的边长表示1CM,三角形的面积是多少?
解:s=2×3÷2=3(平方厘米)
变式2:如下图,每相邻三个点所形成的三角形都是面积为1的等边三角形,计算△ABC的面积.
分析 这是个三角形,虽然有三角形面积公式可用,但判断它的底和高却十分困难,只能另想别的办法:这个三角形是处在长是6、宽是4的矩形内,除此之外还有其他三个直角三角形,如下图(b),这三个直角三角形面积很容易求出,再用矩形面积减去这三个直角三角形面积,就是所要求的三角形面积.
解:矩形面积是6×4=24.
直角三角形I的面积是:
6×2÷2=6.
直角三角形Ⅱ的面积是:4×2÷2=4,
直角三角形Ⅲ的面积是:4×2÷2=4.
所求三角形的面积是:
24-(6+4+4)=10
三、课堂总结
找准三角形的各边,牢记公式,灵活运用上解决三角形问题的关键和方法。
课后作业
1.比一比下面两个图形的面积。结果是( )。
① ② A.①>②
B. ①<②
C. ①=②
答案C
2.若图中涂色部分代表240元,则全部代表多少钱?
分析,可以算出一个小三角形代表多少,则可以算出全部
解:240÷4×9=540元
3.如图ABFE和CDEF都是长方形,AB的长是4厘米,BC的长是3厘米,那么图中阴影部分的面积是多少平方厘米?
分析:根据三角形等底等高的性质,可以得出阴影部分的面积和空白一样。
解:s=4×3÷2=6(平方厘米)
4.一块正方形菜地,边长20m,平均分成两块三角形菜地,其中一块种白菜,另一块种菠菜,已知每平方米可以收获白菜10kg,菠菜6kg,问这块地收获白菜菠菜个多少千克?
解:三角形的面积s=20×20÷2=200(平方米)
收获白菜:200x10=2000kg
收获菠菜:200x6=1200kg
5.已知三角形ABC的面积为1,BE=2AB,BC=CD,求三角形BDE的面积?(下页图)
分析,见右图,连结CE.对于三角形ABC与三角形BEC,分别把AB和BE可知,S△BEC=2S△ABC=2.显然,三角形BEC和三角形CED是两个等底(BC=CD)、等高的三角形,因此 S△CED=S△BEC=2。 这样,S△BDE=S△BEC+S△CED=4。
长方形
一、知识梳理
四个角都是直角的平行四边形叫做长方形
(1)特征
长方形有四条边,对边相等,4个角都是直角的四边形。
长方形长边的长叫作长,短边的长叫宽。
长方形是轴对称图形,它有两条对称轴。
(2)计算公式
周长=(长+宽)×2
字母表示为:
c=2(a+b)
面积=长×宽
字母表示为:
s=ab
二、例题精讲
例1:求长方形的周长和面积
35cm
20cm
5dm
12dm
分析:对于单一的题目,直接带公式:
c=(35+20)×2=55x2=110cm s=35x20=700
30厘米
21厘米
C=(5+12)x2=17x2=34dm s=5x12=60
例2:一张长方形的A4纸(如下图),它的面积是多少
平方厘米?
30×21=630(平方厘米)
变式1:如果从这张纸上剪下一个最大的正方形,
这个正方形的面积是多少?
21×21=441(平方厘米)
变式2:如果从这张纸上剪下一个最大的正方形,剩下的面积是多少?
630-441=169(平方厘米)
例3:小红用一根长 8 厘米的铁丝,围成一个最大的正方形,这个正方形的边长是多少?面积是多少?
分析,要正方形最大,则48即周长,根据公式计算边长,然后计算面积。
解:8÷4=2厘米
2×2=4平方厘米
变式1:小红用一根长铁丝围成一个正方形,这个正方形的面积是16平方厘米。它的周长是多少?边长是多少?
解:16=4×4,所以边长是4厘米
C=4×4=16厘米
变式2:小红用n个长3厘米,宽x厘米的长方形拼车一个正方形,正方形的周长12厘米,求整数x和n?
解:12÷4=3 所以边长为3,长大于宽,所以x=1或者x=2
1)若x=1,则n=3
2)若x=2,则n=2
花圃
例4:小区前面有一块60米边长的正方形空坪,现要在空坪的中间做一个长32米、宽28米的长方形花圃,其余的植上草皮.(如下图)
花圃的面积是多少平方米?草皮的面积是多少平方米?
解:花圃:32×28=896平方米
草皮:60×60-896=2704平方米
变式1:小区前面有一块长60米,宽40米的长方形草地,现在修一条平行于长的长方形小路,宽2m,问草地面积还有多少?
解:
S=(40-2)×60=2280平方米
变式2:小区前面有一块长60米,宽40米的长方形草地,现在修两条分别平行于长和宽的长方形小路,小路宽2m,问草地面积还有多少?
解:
S=(60-2)×(40-2)=2204平方米
例5:一块广告牌长6米,宽2米,如果每平方米用油漆2千克,这块广告牌一共要用多少千克油漆?
分析:知道每平方米用油漆2千克,只要算出有多少面积即可
解:S=6×2=12平方米
12×2=24千克
变式1:一间长方形会议室长12米,宽6米。这个会议室地板面积是多少平方米?合多少平方分米?如果一块地砖的面积是9平方分米,铺完这间会议室地板至少要用多少块这样的地砖?
解:12×6=72平方米=7200平方分米
7200÷9=800块
变式2:一间长方形会议室长12米,宽6米。这个会议室地板面积是多少平方米?合多少平方分米?如果一块正方形地砖的边长是3分米,铺完这间会议室地板至少要用多少块这样的地砖?
解:12×6=72平方米=7200平方分米
36×3=9平方分米
7200÷9=800块
三、课堂总结
在解决长方形问题的时候要抓住其特征进行条件查找,在记住公式的同时灵活运用在解题上面。
四、课后作业
一块长方形菜地,长20米,宽8米。如果要给这块菜地围上篱笆,篱笆的长是多少米?
答案:(20+8)×2=56m
9
4
5
5
7
2
2.计算下面图形的面积。
9×4=36(平方厘米) 5×5=25(平方厘米)
有一个长方形田地。长是600米,宽是300米,面积是多少公顷?如果围上篱笆,篱笆的长是多少米?如果每公顷收白菜150吨,可以收白菜多少吨?
答案:s=600×300=180000平方米=18公顷
C=(600+300)×2=1800米
18×150=2700吨
4.一个零件形状如图,计算它的周长和面积。(单位:厘米)
6
14
14
6
答案:整体看
s=14×14-6×6=108平方厘米
C=14×4=56厘米
5.一洒水车,每分钟行驶200米,洒水的宽度是10米,洒水车行驶6分钟,能给多大的地面洒上水?
答案:6×200×10=12000平方米
正方形
一、知识梳理
长和宽相等的长方形是正方形。
(1)特征:
四条边都相等,四个角都是直角的四边形。
正方形每条边的长叫作边长。
正方形是轴对称图形,它有4条对称轴。正方形还是中心对称图形。
(2)计算公式
周长=边长x4
用字母表示:
c=4a
面积=边长x边长
用字母表示:
s=a × a=
二、例题精讲
例1:
边长:16米 边长:300厘米
面积:16×16=256平方米 面积:300×300=90000平方厘米
周长:16×4=64米 周长:300×4=1200厘米
例2:把一个长10厘米,宽3厘米的长方形硬纸剪成面积尽可能大的正方形,可以剪( )。
A.1个 B.2个 C.3个
分析,长方形的长是宽的3倍还多1,所以可以剪3个
选C
变式1:5个边长1m的正方形拼在一起构成一个长方形,周长是多少?
C=(5+1)×2=12m
变式2: 用6个边长1m的正方形拼在一起构成一个长方形,周长是多少?
分析:6个正方形可以分2排或者1排,所以有两种情况
c=(6+1)×2=14m
C=(2+3)×2=10m
例3:用边长1厘米的小正方形拼成图形 ,它的周长是( ),面积是( )。
分析:图形可以通过移动边使其变成一个长方形c=(2+3)×2=10。面积没有变化
答案:10厘米,4平方厘米
变式1:用边长1厘米的小正方形拼成图形,它的周长是( ),面积是( )。
C=(2+5)×2-1=13厘米
S=5+2=7平方厘米
变式2:用边长1厘米的小正方形拼成图形,它的周长是( ),面积是( )。
解:
C=(3+5)×2=16厘米
S=3+3+5=11平方厘米
例4:小明家的客厅长5米,宽4米。地面上铺有边长为5分米的正方形地砖。铺这个客厅,需要多少块地砖?
分析:先换算单位,根据面积相等计算
解:5米=50分米 4米=40分米
50×40÷(5×5)
=2000÷25
=80(块)
变式1:小明家的客厅长5米,宽4米。地面上铺有边长为5分米的正方形地砖,这种地砖20元一块。铺这个客厅,需要多少块地砖?买这些地砖共需多少钱?
由上题可以知道需要80块
解:
总钱=80×20=1600元
变式2:小明家的客厅长5米,宽4米。地面上铺有边长为5分米的正方形地砖,铺这个客厅,买这些地砖共需1600元。这种地砖多少元一块?
计算单价,有总价除以块数
解:
1600÷80=20元
例5:小红用一根长 48 厘米的铁丝,围成一个最大的正方形,这个正方形的边长是多少?面积是多少?
分析,要正方形最大,则48即周长,根据公式计算边长,然后计算面积。
解:48÷4=12厘米
12×12=144平方厘米
变式1:小红用一根长铁丝围成一个正方形,这个正方形的面积是144平方厘米。它的周长是多少?边长是多少?
解:144=12×12,所以边长是12厘米
C=12×4=48厘米
变式2:小红用3个长3厘米,宽2厘米的长方形拼车一个正方形,求正方形的周长和面积?
解:c=3×4=12厘米
S=3×2×3=18平方厘米
三、课堂总结
解决正方形问题的时候要抓住其特征进行条件查找,灵活运用。
四、课后作业
1.求下面长方形的周长和面积:(单位:厘米)
5 4
1
周长:12厘米 周长:16厘米
面积: 5平方厘米 面积:16平方厘米
6
6
6×6=36(平方厘)米)
9×2=18(平方厘)米)
9
2
7
8×7=56(平方厘米)
2.求下图的面积
3.用18个边长为1厘米的小正方形拼成一个长方形,要使长方形的周长最大应怎样拼?周长最小呢?请画出图,并列式计算。
解
要是周长最大,则需要一字排开
C=(1+18)×2=38cm
要是周长最小,则需要尽可能的靠拢:如图
C=(3+6)×2=18cm
4.足球场是一个长方形,长 100 米,宽 75 米,小明沿着足球场跑了 2 圈,跑了多少米?
解:c=(100+75)×2=350m
一块长方形菜地,长6米,宽4米。四周围上篱笆,篱笆长多少米?如果一面靠墙,篱笆至少要多少米?
答案:20m,14m
平行四边形
一、知识梳理
有两组对边分别平行的四边形是平行四边形。
(1) 特征
相对的边平行且相等。对角相等,相邻的两个角的度数之和为180度。平行四边形容易变形。
(2) 计算公式
平行四边形的面积=底×高
用字母表示:
s=ah
二、例题精讲
例1:右图中有( )个平行四边形,
答案:3
变式1:下图中有( )个平行四边形
答案:9
变式2:下图中有( )个平行四边形
答案:13
例2:计算下面各个平行四边的面积。(单位:m)
S1=2.8×1.2=3.36平方米
S2=1.6×0.8=1.28平方米
例3: 一平行四边形的底27厘米,高12.5厘米;另一条底18厘米,这条底边上的高是多少厘米?
分析,根据面积相等即可求得。
27×12.5=337.5(厘米2)
337.5÷18=18.75(厘米)
答:这条底边上的高是18.75厘米。
变式1:一平行四边形的底24厘米,高是底的一半;另一条底18厘米,这条底边上的高是多少厘米?
24×24÷2÷18=16厘米
变式2:一平行四边形的面积是18平方厘米,高是底的一半;另一条底是前一条底的一半,另一条底边上的高是多少厘米?
18÷2=9 9=3×3
所以,底是3厘米,高6厘米
6×2=12厘米
答:另一条底边上的高是12厘米.
例4:把一个长方形拉成平行四边形后,它的面积( )
A比原来大 C比原来小
B与原来相等 D无法确定
分析,长方形边长平行四边形后,高变小,所以选C
变式1:把一个平行四边形拉成长方形后,它的面积( )
A比原来大 C比原来小
B与原来相等 D无法确定
分析,长方形边长平行四边形后,高变小,反之选A
变式2:把一个长方形拉成平行四边形后,它的面积变成原来的一半,则高怎么变化
答:高变为原来的一半
例5:如图,两个边长10厘米的正方形相互错开3厘米,那么图中阴影平行四边形的面积是多少?
分析:阴影部分的面积等于总面积减去四个小三角形的面积。
S=10×10×2-10×10-3×3
=91平方厘米
变式1:上题中,当正方形错开5厘米时,阴影面积是多少?
S=10×10×2-10×10-5×5
=75平方厘米
变式2:上题中,当正方形大约错开多少厘米时,阴影面积是总面积的四分之一?
由题意得:50=10×10×2-10×10-n×n
n≈7cm
课堂总结
图形面积的计算属于较简单的问题,找准数量关系是解题的关键。
四、课后作业
1.已知下图中正方形的周长是36厘米,求平行四边形的面积。
36÷4=9(厘米)
9×9=81(平方厘米)
2.平行四边形的面积是36.8平方分米,高是2.3分米,底是多少?
a = s÷h
= 36.8÷2.3
= 16(分米)
答:底是16分米。
3.一块平行四边形的菜地,底是30米,高是21米。如果每棵大白菜占地9平方分米,这块地一共可种多少棵大白菜?
30×21=630(平方米)
630平方米=63000平方分米
63000÷9=7000(棵)
答:这块地一共可种7000棵大白菜。
4.一块平行四边形的铁皮的周长是82厘米,一条底长是16厘米,这条底上的高是20厘米,求另一条底上的高是多少厘米?
82÷2-16=25(厘米)
16×20÷25=12.8(厘米)
5.如右图,四边形ABCD和DEFG都是平行四边形,证明它们的面积相等
证明:连结CE,平行四边形ABCD的面积等于△CDE面积的2倍,而平行四边形DEFG的面积也是△CDE面积的2倍。
∴平行四边形ABCD的面积与平行四边形DEFG的面积相等。
梯形
一、知识梳理
梯形:指一组对边平行而另一组对边不平行的四边形叫做梯形。
上底
①上底、下底:平行的两边叫做梯形的底边,其中长边叫下底,短边叫上底;
高
②腰:不平行的两边叫腰;
③高:夹在两底之间的垂线段叫梯形的高。
下底
(1)特征
只有一组对边平行的四边形。
中位线等于上下底和的一半。
两腰相等的梯形是等腰梯形,等腰梯形有一条对称轴。
(2) 公式
梯形的面积:(上底+下底)×高÷2
用字母表示:
s=(a+b)h/2
二、例题精讲
20
32
20
例1:计算下面各梯形的面积。(单位:厘米)X k
分析:直接带入公式
解:
(15+20)×8÷2 =140(平方厘米)
(20+32)×20÷2 =520(平方厘米)
例2:有一块梯形花地,上底是8米,下底是10米,高是4.8米。已知每株花占地0.06平方米,这块地能种花多少株?
分析:先计算面积,然后计算株数。
解:(8+10)×4.8÷2÷0.06=720(株)
变式1:有一块梯形花地,上底是8米,下底是10米,高是4.8米。已知,这块地能种花720株,每株花占地多少平方米?
解:(8+10)×4.8÷2÷720=0.06(平方米)
变式2:有一块梯形花地,上底是8米,下底是10米。已知,这块地能种花720株且每株花占地0.06平方米,问高是多少米?
解:设高是h:
(8+10)×h÷2÷720=0.06
解得h=4.8m
例3:一个梯形的上底是12分米,高是8分米,面积是108平方分米。这个梯形的下底是多上分米?
分析:根据面积公式求解。
解:108×2÷8-12=15(分米)
变式1:一个梯形的上底是12分米,下底是15分米,面积是108平方分米。这个梯形的高是多少分米?
解:h=108×2÷(12+15)
=8dm
变式2:一个梯形的上底是12分米,下底是上底的2倍,面积是108平方分米。这个梯形的高是多少分米?
解:h=108×2÷(12+12×2)
=6dm
例4:已知梯形的面积是20平方分米,求阴影部分的面积。
3.2分米
解:20×2÷(3.2+6.8)=4(分米)
变式1:如图所示,大正方形的边长是12米,小正方形的边长是5米,求阴影部分的面积。
w W w . x K b 1.c o M
解:(5+12)×12÷2=102(平方米)
变式2:图中,阴影部分的面积是13.5平方厘米,着个梯形的面积是多少?
7厘米
解:13.5×2÷9=3(厘米)
(7+9)×3÷2=24(平方厘米)
例5:用篱笆围城一个梯形养鸡场,一边利用房屋的墙壁,篱笆的 长是65米,求养鸡长得面积。
X k B 1 . c o m
15米
解:(65-15)×15÷2=375(平方米)
变式1:上题中,若上底是下底的3倍,则上底是多少?
(65-15)÷(1+3)=10m
变式2:如下图,若梯形上底是下底的3倍,面积是300平方米,则高是多少?
15米
解:h=300×2÷(15+15×3)
=10m
课堂总结
牢记梯形的面积公式。熟练运用。
四、课后作业
1、可以把一个梯形分成两个( )形,也可以分成一个( )形和一个( )形。
2、梯形的上底长8厘米,下底长14厘米,高是上底的一半。梯形的面积是( )平方厘米。
3、两个完全一样的梯形拼成的一个平行四边形的面积是80平方厘米,高是5厘米,梯形的上底是7厘米,梯形的下底是( )厘米。
4、一个梯形上下底的和是16米,高是7米,它的面积是( )
5、判断下列各题,对的打√,错的打×
(1)两个面积一样的梯形一定可以拼成一个平行四边形 ( )
(2)平行四边形的面积是梯形面积的两倍( )
(3)计算一个梯形的面积,比武知道他的上下底和高 ( )
(4)一个梯形两底的和是12米,高是10米,则它的面积是60平方米 ( )
答案:1.三角形, 三角形, 平行四边形 2. 44 3. 9 4. 56 5.××√√
5.如图,梯形ABCD的面积是45平方米,高6米,△AED的面积是5平方米,BC=10米,求阴影部分面积.
解:∵梯形面积=(上底+下底)×高÷2
即45=(AD+BC)×6÷2,
45=(AD+10)×6÷2,
∴AD=45×2÷6-10=5米。
∴△ADE的高是2米。
△EBC的高等于梯形的高减去△ADE的高,
即6-2=4米,
S=BC×4÷2=20平方米
圆
一、知识梳理
(1)圆
到定点的距离等于定长的所有点组成的图形。
圆中心的一点叫做圆心。一般用字母o表示。
半径:连接圆心和圆上任意一点的线段叫做半径。一般用r表示。
在同一个圆里,有无数条半径,每条半径的长度都相等。
通过圆心并且两端都在圆上的线段叫做直径。一般用d表示。
同一个圆里有无数条直径,所有的直径都相等。
同一个圆里,直径等于两个半径的长度,即d=2r。
圆的大小由半径决定。 圆有无数条对称轴。
(2)圆的画法
把圆规的两脚分开,定好两脚间的距离(即半径);
把有针尖的一只脚固定在一点(即圆心)上;
把装有铅笔尖的一只脚旋转一周,就画出一个圆。
(3) 圆的周长
围成圆的曲线的长叫做圆的周长。
把圆的周长和直径的比值叫做圆周率。用字母∏表示。
(4) 圆的面积
圆所占平面的大小叫做圆的面积。
(5)计算公式
d=2r
r=d/2
c=∏d
c=2∏r
s=∏r?
二、例题精讲
例1:求下列圆的周长及面积。
(半径3) (直径12)
周长:2×3.14×3=18.84 周长:3.14×12=37.68
面积:3.14×3×3=28.26面积:3.14×(12÷2)×(12÷2)=113.04
例2:圆形草坪的半径是10m,每平方米草皮8元,铺满需要多少钱?
分析:先求出面积,即可求得钱数。
解3.14×10×10=314平方米
314×8=2512元
变式1:圆形草坪的直径是20m,每平方米草皮8元,铺满需要多少钱?
解:20÷2=10米
3.14×10×10=314平方米
314×8=2512元
变式2:圆形草坪的直径是20m,铺满需要钱2512元,每平方米草皮多少元?
解:20÷2=10米
3.14×10×10=314平方米
2512÷314=8元
例3:光盘的银色部分是一个圆环,内圆半径是2cm,外圆半径是6cm。内圆的面积是多少?
分析:直接带公式
解:S=3.14×2?
变式1:光盘的银色部分是一个圆环,内圆半径是2cm,外圆半径是6cm。外圆的面积是多少?
解:s=3.14×6?
变式2:光盘的银色部分是一个圆环,内圆半径是2cm,外圆半径是6cm。圆环的面积是多少?
解:方法一: 3.14×6?-3.14×2?
=113.04-12.56
=100.48(cm?)
方法二:3.14×(6?-2?)
=3.14×32
=100.48(cm?)
例4:公园里有一棵大树,同学们用一根20米长的绳子围绕这棵树绕了6圈,还剩下1.16米,求树干的直径是多少?
分析:6圈其实就是树周长的6倍,由此建立等式:
解:(20-1.16)÷6÷3.14
=1m
变式1:公园里有一棵大树,同学们用一根20米长的绳子围绕这棵树绕了几圈,还剩下1.16米,树干的直径是1m,求大家绕了多少圈?
解:(20-1.16)÷1÷3.14
=6圈
变式2:公园里有一棵大树,同学们用一根长的绳子围绕这棵树绕了6圈,还剩下1.16米,树干的直径是1m,求绳子有多少米?
解:3.14×1×6+1.16=20米
例5:一个运动场如右图所示,两端是半圆形,中间是长方形。
小海在运动场上跑2圈,一共跑了多少米?
分析:操场周长可以看成一个圆周加上一个长方形的两个长。
解:L=(100+100+3.14×60)×2
=388.4×2
=776.8m
变式1:一个运动场如右图所示,两端是半圆形,中间是长方形。小海在运动场上跑了776.8米,一共跑了多少圈?
解:(776.8÷2-200)÷3.14÷60=2圈
变式2:一个运动场如右图所示,两端是半圆形,中间是长方形。小海和小明在运动场上同向而跑,6分钟时,小海跑2圈而小明跑了2圈半,问他们的速度差?
解:L1=(100+100+3.14×60)×2
=388.4×2
=776.8m
L2=(100+100+3.14×60)×2.5
=388.4×2.5
=971m
小海的速度:776.8÷6=129.47m/min
小明的速度:971÷6=161.83m/min
速度差:161.83-129.47=32.36m/min
课堂总结
在圆一个小节,要注意审题,看清楚是直径还是半径,牢记公式,认真书写。
四、课后作业
1. 一个圆形茶几桌面的直径是1m,它的面积是多少平方米?
2. 一个圆形环岛的直径是50m,中间是一个直径为10m的圆形花坛,其他地方是草坪。草坪的占地面积是多少?
3.看图求出阴影部分的面积。(单位:厘米)
10
15
6
6
4.为美化校园,学校在教学楼前修了一个周长是31.4m的圆形花坛,围绕花坛铺了一条2m宽的环形小路。这条小路的面积是多少平方米?
5.一个圆和一个正方形,它们的周长相等,它们的面积相比较是( )。
A.圆的面积大 B.正方形的面积大 C. 面积同样大
6.如果两个圆的半径之比是2:3,那么这两个圆的面积之比是( )
A.2:3 B.3:2 C.4:9
7.车轮滚动一周,求所行驶的路程就是求车轮的( )。
A.直径 B.周长 C. 面积
附:
单位换算
熟记基本换算关系: 高级单位化低级单位:×进率 低级单位聚高级单位:÷进率
(长度单位):1千米=1000米????1米=10分米 1分米=10厘米
1厘米=10毫米 1米=100厘米??? ?? 1米=1000毫米
(面积单位):1平方千米=100公顷 1公顷=10000平方米
1平方米=100平方分米 1平方分米=100平方厘米
1平方厘米=100平方毫米
专题讲解+配套练习
小升初数学专题复习
小升初
第四-五讲 平面图形的特征及计算-教师版
三角形
一、知识梳理
由三条线段围成的图形(每相邻两条线段的端点相连)叫做三角形。
(1)特征
三角形都有三条边、三个顶点、三个角;
三角形内角和是180度。
从三角形的一个顶点到它的对边做一条垂线,顶点和垂足之间的线段叫三角形的高,这条对边叫做三角形的底。三角形有三条高。
三角形具有稳定性。
(2)计算公式
三角形面积:三角形面积=底×高÷2
用字母表示:
s=ah/2
(3) 分类
按角分
锐角三角形 :三个角都是锐角。
直角三角形 :有一个角是直角。等腰三角形的两个锐角各为45度,它有一条对称轴。
钝角三角形:有一个角是钝角。
按边分
不等边三角形:三条边长度不相等。
等腰三角形:有两条边长度相等;两个底角相等;有一条对称轴。
等边三角形:三条边长度都相等;三个内角都是60度;有三条对称轴。
二、例题精讲
例1:求下列三角形的面积。(单位m)
15
12
15
15
12
10
解析:直接带入三角形的面积公式:s=ah/2
解1:s=10×12÷2=120÷2=60
2:s=15×15÷2=225÷2=112.5
3:s=12×15÷2=180÷2=90
总结:计算三角形面积的时候,找准底和高,直接带入公式。
变式1:如图:求三角形的面积:
分析:本题要找准三角形的高是谁,底是谁,要知道底和高的垂直关系则可以找到底是4cm,高是3cm。带入公式
解:s=ah÷2=3×4÷2=6
变式2:已知等腰三角形的底边上的高是8cm,底边是高的1.5倍,求三角形的面积。
解:s=ah÷2=8×8×1.5÷2=48
8
6
例2:把大、小两个正方形拼在一起,它们的边长分别是8米和6米,那么图中阴影部分的面积是多少平方米?
分析:本题首先要找准底和高。然后直接带公式。
解:s=ah/2=(8-6)×6÷2=6
变式1:如图,求图中阴影部分的面积是多少平方米?
10
7
解:s=ah/2=(10-7)×7÷2=10.5
变式2:如图:求图中阴影部分的面积是多少平方米?
6
8
解:s=ah/2=6×6÷2=18
例3:如图,平行四边形ABCD的面积是32平方厘米,三角形CED是一个直角三角形,已知AE=5厘米,CE=4厘米,那么阴影部分的面积是多少平方厘米?E
A
B
C
D
分析:可以把平行四边形分成一个矩形和2个相等的三角形,用总面积减去矩形的面积除以2即可:
解:s=(32-5×4)÷2
=12÷2
=6(平方厘米)
变式1:如上图:若四边形ABCE的面积是26平方厘米,AE=5厘米,CE=4厘米,那么阴影部分的面积是多少平方厘米?
解:s=26-5×4
=26-20
=6(平方厘米)
变式2:在上题中,已知平行四边形ABCD的面积是32平方厘米,无其余条件,则阴影三角形的面积最大是多少?
解:S=32÷2=16(平方厘米)
例4:如图,在平行四边形ABCD中,三角形BCE的面积是42平方厘米,BC的长度为14厘米,AE的长度为9厘米,三角形ECD的面积又是多少平方厘米?
A
B
C
D
E
分析:知道三角形BCE的面积和BC的长度,则可以求高,AE=9,求得ED=5,则可以直接带公式。
解:s=42x2÷14x(14-9)÷2
=15(平方厘米)
变式1:如上图,三角形ECD的面积是15平方厘米,BC的长度为14厘米,AE的长度为9厘米,三角形BCE的面积又是多少平方厘米?
解:三角形的高h=14x2÷(14-9)=6cm
S=14x6÷2=42(平方厘米)
变式2:如上图,若有一平行四边形菜地,总面积是42平方米,共收获420kg白菜,则三角形ECD菜地大约收获多少白菜?
分析:收获的菜与其面积成正比,面积越大则收获的越多。
解s=42x2÷14x(14-9)÷2
=15(平方米)
收获白菜:420÷42x15=150kg
例5:每个小方格的边长表示1CM,三角形的面积是多少?
分析:由图可以看出,三角形的底边是7,高是4带入公式
S=7×4÷2=14(平方厘米)
变式1:如下图,每个小方格的边长表示1CM,三角形的面积是多少?
解:s=2×3÷2=3(平方厘米)
变式2:如下图,每相邻三个点所形成的三角形都是面积为1的等边三角形,计算△ABC的面积.
分析 这是个三角形,虽然有三角形面积公式可用,但判断它的底和高却十分困难,只能另想别的办法:这个三角形是处在长是6、宽是4的矩形内,除此之外还有其他三个直角三角形,如下图(b),这三个直角三角形面积很容易求出,再用矩形面积减去这三个直角三角形面积,就是所要求的三角形面积.
解:矩形面积是6×4=24.
直角三角形I的面积是:
6×2÷2=6.
直角三角形Ⅱ的面积是:4×2÷2=4,
直角三角形Ⅲ的面积是:4×2÷2=4.
所求三角形的面积是:
24-(6+4+4)=10
三、课堂总结
找准三角形的各边,牢记公式,灵活运用上解决三角形问题的关键和方法。
课后作业
1.比一比下面两个图形的面积。结果是( )。
① ② A.①>②
B. ①<②
C. ①=②
答案C
2.若图中涂色部分代表240元,则全部代表多少钱?
分析,可以算出一个小三角形代表多少,则可以算出全部
解:240÷4×9=540元
3.如图ABFE和CDEF都是长方形,AB的长是4厘米,BC的长是3厘米,那么图中阴影部分的面积是多少平方厘米?
分析:根据三角形等底等高的性质,可以得出阴影部分的面积和空白一样。
解:s=4×3÷2=6(平方厘米)
4.一块正方形菜地,边长20m,平均分成两块三角形菜地,其中一块种白菜,另一块种菠菜,已知每平方米可以收获白菜10kg,菠菜6kg,问这块地收获白菜菠菜个多少千克?
解:三角形的面积s=20×20÷2=200(平方米)
收获白菜:200x10=2000kg
收获菠菜:200x6=1200kg
5.已知三角形ABC的面积为1,BE=2AB,BC=CD,求三角形BDE的面积?(下页图)
分析,见右图,连结CE.对于三角形ABC与三角形BEC,分别把AB和BE可知,S△BEC=2S△ABC=2.显然,三角形BEC和三角形CED是两个等底(BC=CD)、等高的三角形,因此 S△CED=S△BEC=2。 这样,S△BDE=S△BEC+S△CED=4。
长方形
一、知识梳理
四个角都是直角的平行四边形叫做长方形
(1)特征
长方形有四条边,对边相等,4个角都是直角的四边形。
长方形长边的长叫作长,短边的长叫宽。
长方形是轴对称图形,它有两条对称轴。
(2)计算公式
周长=(长+宽)×2
字母表示为:
c=2(a+b)
面积=长×宽
字母表示为:
s=ab
二、例题精讲
例1:求长方形的周长和面积
35cm
20cm
5dm
12dm
分析:对于单一的题目,直接带公式:
c=(35+20)×2=55x2=110cm s=35x20=700
30厘米
21厘米
C=(5+12)x2=17x2=34dm s=5x12=60
例2:一张长方形的A4纸(如下图),它的面积是多少
平方厘米?
30×21=630(平方厘米)
变式1:如果从这张纸上剪下一个最大的正方形,
这个正方形的面积是多少?
21×21=441(平方厘米)
变式2:如果从这张纸上剪下一个最大的正方形,剩下的面积是多少?
630-441=169(平方厘米)
例3:小红用一根长 8 厘米的铁丝,围成一个最大的正方形,这个正方形的边长是多少?面积是多少?
分析,要正方形最大,则48即周长,根据公式计算边长,然后计算面积。
解:8÷4=2厘米
2×2=4平方厘米
变式1:小红用一根长铁丝围成一个正方形,这个正方形的面积是16平方厘米。它的周长是多少?边长是多少?
解:16=4×4,所以边长是4厘米
C=4×4=16厘米
变式2:小红用n个长3厘米,宽x厘米的长方形拼车一个正方形,正方形的周长12厘米,求整数x和n?
解:12÷4=3 所以边长为3,长大于宽,所以x=1或者x=2
1)若x=1,则n=3
2)若x=2,则n=2
花圃
例4:小区前面有一块60米边长的正方形空坪,现要在空坪的中间做一个长32米、宽28米的长方形花圃,其余的植上草皮.(如下图)
花圃的面积是多少平方米?草皮的面积是多少平方米?
解:花圃:32×28=896平方米
草皮:60×60-896=2704平方米
变式1:小区前面有一块长60米,宽40米的长方形草地,现在修一条平行于长的长方形小路,宽2m,问草地面积还有多少?
解:
S=(40-2)×60=2280平方米
变式2:小区前面有一块长60米,宽40米的长方形草地,现在修两条分别平行于长和宽的长方形小路,小路宽2m,问草地面积还有多少?
解:
S=(60-2)×(40-2)=2204平方米
例5:一块广告牌长6米,宽2米,如果每平方米用油漆2千克,这块广告牌一共要用多少千克油漆?
分析:知道每平方米用油漆2千克,只要算出有多少面积即可
解:S=6×2=12平方米
12×2=24千克
变式1:一间长方形会议室长12米,宽6米。这个会议室地板面积是多少平方米?合多少平方分米?如果一块地砖的面积是9平方分米,铺完这间会议室地板至少要用多少块这样的地砖?
解:12×6=72平方米=7200平方分米
7200÷9=800块
变式2:一间长方形会议室长12米,宽6米。这个会议室地板面积是多少平方米?合多少平方分米?如果一块正方形地砖的边长是3分米,铺完这间会议室地板至少要用多少块这样的地砖?
解:12×6=72平方米=7200平方分米
36×3=9平方分米
7200÷9=800块
三、课堂总结
在解决长方形问题的时候要抓住其特征进行条件查找,在记住公式的同时灵活运用在解题上面。
四、课后作业
一块长方形菜地,长20米,宽8米。如果要给这块菜地围上篱笆,篱笆的长是多少米?
答案:(20+8)×2=56m
9
4
5
5
7
2
2.计算下面图形的面积。
9×4=36(平方厘米) 5×5=25(平方厘米)
有一个长方形田地。长是600米,宽是300米,面积是多少公顷?如果围上篱笆,篱笆的长是多少米?如果每公顷收白菜150吨,可以收白菜多少吨?
答案:s=600×300=180000平方米=18公顷
C=(600+300)×2=1800米
18×150=2700吨
4.一个零件形状如图,计算它的周长和面积。(单位:厘米)
6
14
14
6
答案:整体看
s=14×14-6×6=108平方厘米
C=14×4=56厘米
5.一洒水车,每分钟行驶200米,洒水的宽度是10米,洒水车行驶6分钟,能给多大的地面洒上水?
答案:6×200×10=12000平方米
正方形
一、知识梳理
长和宽相等的长方形是正方形。
(1)特征:
四条边都相等,四个角都是直角的四边形。
正方形每条边的长叫作边长。
正方形是轴对称图形,它有4条对称轴。正方形还是中心对称图形。
(2)计算公式
周长=边长x4
用字母表示:
c=4a
面积=边长x边长
用字母表示:
s=a × a=
二、例题精讲
例1:
边长:16米 边长:300厘米
面积:16×16=256平方米 面积:300×300=90000平方厘米
周长:16×4=64米 周长:300×4=1200厘米
例2:把一个长10厘米,宽3厘米的长方形硬纸剪成面积尽可能大的正方形,可以剪( )。
A.1个 B.2个 C.3个
分析,长方形的长是宽的3倍还多1,所以可以剪3个
选C
变式1:5个边长1m的正方形拼在一起构成一个长方形,周长是多少?
C=(5+1)×2=12m
变式2: 用6个边长1m的正方形拼在一起构成一个长方形,周长是多少?
分析:6个正方形可以分2排或者1排,所以有两种情况
c=(6+1)×2=14m
C=(2+3)×2=10m
例3:用边长1厘米的小正方形拼成图形 ,它的周长是( ),面积是( )。
分析:图形可以通过移动边使其变成一个长方形c=(2+3)×2=10。面积没有变化
答案:10厘米,4平方厘米
变式1:用边长1厘米的小正方形拼成图形,它的周长是( ),面积是( )。
C=(2+5)×2-1=13厘米
S=5+2=7平方厘米
变式2:用边长1厘米的小正方形拼成图形,它的周长是( ),面积是( )。
解:
C=(3+5)×2=16厘米
S=3+3+5=11平方厘米
例4:小明家的客厅长5米,宽4米。地面上铺有边长为5分米的正方形地砖。铺这个客厅,需要多少块地砖?
分析:先换算单位,根据面积相等计算
解:5米=50分米 4米=40分米
50×40÷(5×5)
=2000÷25
=80(块)
变式1:小明家的客厅长5米,宽4米。地面上铺有边长为5分米的正方形地砖,这种地砖20元一块。铺这个客厅,需要多少块地砖?买这些地砖共需多少钱?
由上题可以知道需要80块
解:
总钱=80×20=1600元
变式2:小明家的客厅长5米,宽4米。地面上铺有边长为5分米的正方形地砖,铺这个客厅,买这些地砖共需1600元。这种地砖多少元一块?
计算单价,有总价除以块数
解:
1600÷80=20元
例5:小红用一根长 48 厘米的铁丝,围成一个最大的正方形,这个正方形的边长是多少?面积是多少?
分析,要正方形最大,则48即周长,根据公式计算边长,然后计算面积。
解:48÷4=12厘米
12×12=144平方厘米
变式1:小红用一根长铁丝围成一个正方形,这个正方形的面积是144平方厘米。它的周长是多少?边长是多少?
解:144=12×12,所以边长是12厘米
C=12×4=48厘米
变式2:小红用3个长3厘米,宽2厘米的长方形拼车一个正方形,求正方形的周长和面积?
解:c=3×4=12厘米
S=3×2×3=18平方厘米
三、课堂总结
解决正方形问题的时候要抓住其特征进行条件查找,灵活运用。
四、课后作业
1.求下面长方形的周长和面积:(单位:厘米)
5 4
1
周长:12厘米 周长:16厘米
面积: 5平方厘米 面积:16平方厘米
6
6
6×6=36(平方厘)米)
9×2=18(平方厘)米)
9
2
7
8×7=56(平方厘米)
2.求下图的面积
3.用18个边长为1厘米的小正方形拼成一个长方形,要使长方形的周长最大应怎样拼?周长最小呢?请画出图,并列式计算。
解
要是周长最大,则需要一字排开
C=(1+18)×2=38cm
要是周长最小,则需要尽可能的靠拢:如图
C=(3+6)×2=18cm
4.足球场是一个长方形,长 100 米,宽 75 米,小明沿着足球场跑了 2 圈,跑了多少米?
解:c=(100+75)×2=350m
一块长方形菜地,长6米,宽4米。四周围上篱笆,篱笆长多少米?如果一面靠墙,篱笆至少要多少米?
答案:20m,14m
平行四边形
一、知识梳理
有两组对边分别平行的四边形是平行四边形。
(1) 特征
相对的边平行且相等。对角相等,相邻的两个角的度数之和为180度。平行四边形容易变形。
(2) 计算公式
平行四边形的面积=底×高
用字母表示:
s=ah
二、例题精讲
例1:右图中有( )个平行四边形,
答案:3
变式1:下图中有( )个平行四边形
答案:9
变式2:下图中有( )个平行四边形
答案:13
例2:计算下面各个平行四边的面积。(单位:m)
S1=2.8×1.2=3.36平方米
S2=1.6×0.8=1.28平方米
例3: 一平行四边形的底27厘米,高12.5厘米;另一条底18厘米,这条底边上的高是多少厘米?
分析,根据面积相等即可求得。
27×12.5=337.5(厘米2)
337.5÷18=18.75(厘米)
答:这条底边上的高是18.75厘米。
变式1:一平行四边形的底24厘米,高是底的一半;另一条底18厘米,这条底边上的高是多少厘米?
24×24÷2÷18=16厘米
变式2:一平行四边形的面积是18平方厘米,高是底的一半;另一条底是前一条底的一半,另一条底边上的高是多少厘米?
18÷2=9 9=3×3
所以,底是3厘米,高6厘米
6×2=12厘米
答:另一条底边上的高是12厘米.
例4:把一个长方形拉成平行四边形后,它的面积( )
A比原来大 C比原来小
B与原来相等 D无法确定
分析,长方形边长平行四边形后,高变小,所以选C
变式1:把一个平行四边形拉成长方形后,它的面积( )
A比原来大 C比原来小
B与原来相等 D无法确定
分析,长方形边长平行四边形后,高变小,反之选A
变式2:把一个长方形拉成平行四边形后,它的面积变成原来的一半,则高怎么变化
答:高变为原来的一半
例5:如图,两个边长10厘米的正方形相互错开3厘米,那么图中阴影平行四边形的面积是多少?
分析:阴影部分的面积等于总面积减去四个小三角形的面积。
S=10×10×2-10×10-3×3
=91平方厘米
变式1:上题中,当正方形错开5厘米时,阴影面积是多少?
S=10×10×2-10×10-5×5
=75平方厘米
变式2:上题中,当正方形大约错开多少厘米时,阴影面积是总面积的四分之一?
由题意得:50=10×10×2-10×10-n×n
n≈7cm
课堂总结
图形面积的计算属于较简单的问题,找准数量关系是解题的关键。
四、课后作业
1.已知下图中正方形的周长是36厘米,求平行四边形的面积。
36÷4=9(厘米)
9×9=81(平方厘米)
2.平行四边形的面积是36.8平方分米,高是2.3分米,底是多少?
a = s÷h
= 36.8÷2.3
= 16(分米)
答:底是16分米。
3.一块平行四边形的菜地,底是30米,高是21米。如果每棵大白菜占地9平方分米,这块地一共可种多少棵大白菜?
30×21=630(平方米)
630平方米=63000平方分米
63000÷9=7000(棵)
答:这块地一共可种7000棵大白菜。
4.一块平行四边形的铁皮的周长是82厘米,一条底长是16厘米,这条底上的高是20厘米,求另一条底上的高是多少厘米?
82÷2-16=25(厘米)
16×20÷25=12.8(厘米)
5.如右图,四边形ABCD和DEFG都是平行四边形,证明它们的面积相等
证明:连结CE,平行四边形ABCD的面积等于△CDE面积的2倍,而平行四边形DEFG的面积也是△CDE面积的2倍。
∴平行四边形ABCD的面积与平行四边形DEFG的面积相等。
梯形
一、知识梳理
梯形:指一组对边平行而另一组对边不平行的四边形叫做梯形。
上底
①上底、下底:平行的两边叫做梯形的底边,其中长边叫下底,短边叫上底;
高
②腰:不平行的两边叫腰;
③高:夹在两底之间的垂线段叫梯形的高。
下底
(1)特征
只有一组对边平行的四边形。
中位线等于上下底和的一半。
两腰相等的梯形是等腰梯形,等腰梯形有一条对称轴。
(2) 公式
梯形的面积:(上底+下底)×高÷2
用字母表示:
s=(a+b)h/2
二、例题精讲
20
32
20
例1:计算下面各梯形的面积。(单位:厘米)X k
分析:直接带入公式
解:
(15+20)×8÷2 =140(平方厘米)
(20+32)×20÷2 =520(平方厘米)
例2:有一块梯形花地,上底是8米,下底是10米,高是4.8米。已知每株花占地0.06平方米,这块地能种花多少株?
分析:先计算面积,然后计算株数。
解:(8+10)×4.8÷2÷0.06=720(株)
变式1:有一块梯形花地,上底是8米,下底是10米,高是4.8米。已知,这块地能种花720株,每株花占地多少平方米?
解:(8+10)×4.8÷2÷720=0.06(平方米)
变式2:有一块梯形花地,上底是8米,下底是10米。已知,这块地能种花720株且每株花占地0.06平方米,问高是多少米?
解:设高是h:
(8+10)×h÷2÷720=0.06
解得h=4.8m
例3:一个梯形的上底是12分米,高是8分米,面积是108平方分米。这个梯形的下底是多上分米?
分析:根据面积公式求解。
解:108×2÷8-12=15(分米)
变式1:一个梯形的上底是12分米,下底是15分米,面积是108平方分米。这个梯形的高是多少分米?
解:h=108×2÷(12+15)
=8dm
变式2:一个梯形的上底是12分米,下底是上底的2倍,面积是108平方分米。这个梯形的高是多少分米?
解:h=108×2÷(12+12×2)
=6dm
例4:已知梯形的面积是20平方分米,求阴影部分的面积。
3.2分米
解:20×2÷(3.2+6.8)=4(分米)
变式1:如图所示,大正方形的边长是12米,小正方形的边长是5米,求阴影部分的面积。
w W w . x K b 1.c o M
解:(5+12)×12÷2=102(平方米)
变式2:图中,阴影部分的面积是13.5平方厘米,着个梯形的面积是多少?
7厘米
解:13.5×2÷9=3(厘米)
(7+9)×3÷2=24(平方厘米)
例5:用篱笆围城一个梯形养鸡场,一边利用房屋的墙壁,篱笆的 长是65米,求养鸡长得面积。
X k B 1 . c o m
15米
解:(65-15)×15÷2=375(平方米)
变式1:上题中,若上底是下底的3倍,则上底是多少?
(65-15)÷(1+3)=10m
变式2:如下图,若梯形上底是下底的3倍,面积是300平方米,则高是多少?
15米
解:h=300×2÷(15+15×3)
=10m
课堂总结
牢记梯形的面积公式。熟练运用。
四、课后作业
1、可以把一个梯形分成两个( )形,也可以分成一个( )形和一个( )形。
2、梯形的上底长8厘米,下底长14厘米,高是上底的一半。梯形的面积是( )平方厘米。
3、两个完全一样的梯形拼成的一个平行四边形的面积是80平方厘米,高是5厘米,梯形的上底是7厘米,梯形的下底是( )厘米。
4、一个梯形上下底的和是16米,高是7米,它的面积是( )
5、判断下列各题,对的打√,错的打×
(1)两个面积一样的梯形一定可以拼成一个平行四边形 ( )
(2)平行四边形的面积是梯形面积的两倍( )
(3)计算一个梯形的面积,比武知道他的上下底和高 ( )
(4)一个梯形两底的和是12米,高是10米,则它的面积是60平方米 ( )
答案:1.三角形, 三角形, 平行四边形 2. 44 3. 9 4. 56 5.××√√
5.如图,梯形ABCD的面积是45平方米,高6米,△AED的面积是5平方米,BC=10米,求阴影部分面积.
解:∵梯形面积=(上底+下底)×高÷2
即45=(AD+BC)×6÷2,
45=(AD+10)×6÷2,
∴AD=45×2÷6-10=5米。
∴△ADE的高是2米。
△EBC的高等于梯形的高减去△ADE的高,
即6-2=4米,
S=BC×4÷2=20平方米
圆
一、知识梳理
(1)圆
到定点的距离等于定长的所有点组成的图形。
圆中心的一点叫做圆心。一般用字母o表示。
半径:连接圆心和圆上任意一点的线段叫做半径。一般用r表示。
在同一个圆里,有无数条半径,每条半径的长度都相等。
通过圆心并且两端都在圆上的线段叫做直径。一般用d表示。
同一个圆里有无数条直径,所有的直径都相等。
同一个圆里,直径等于两个半径的长度,即d=2r。
圆的大小由半径决定。 圆有无数条对称轴。
(2)圆的画法
把圆规的两脚分开,定好两脚间的距离(即半径);
把有针尖的一只脚固定在一点(即圆心)上;
把装有铅笔尖的一只脚旋转一周,就画出一个圆。
(3) 圆的周长
围成圆的曲线的长叫做圆的周长。
把圆的周长和直径的比值叫做圆周率。用字母∏表示。
(4) 圆的面积
圆所占平面的大小叫做圆的面积。
(5)计算公式
d=2r
r=d/2
c=∏d
c=2∏r
s=∏r?
二、例题精讲
例1:求下列圆的周长及面积。
(半径3) (直径12)
周长:2×3.14×3=18.84 周长:3.14×12=37.68
面积:3.14×3×3=28.26面积:3.14×(12÷2)×(12÷2)=113.04
例2:圆形草坪的半径是10m,每平方米草皮8元,铺满需要多少钱?
分析:先求出面积,即可求得钱数。
解3.14×10×10=314平方米
314×8=2512元
变式1:圆形草坪的直径是20m,每平方米草皮8元,铺满需要多少钱?
解:20÷2=10米
3.14×10×10=314平方米
314×8=2512元
变式2:圆形草坪的直径是20m,铺满需要钱2512元,每平方米草皮多少元?
解:20÷2=10米
3.14×10×10=314平方米
2512÷314=8元
例3:光盘的银色部分是一个圆环,内圆半径是2cm,外圆半径是6cm。内圆的面积是多少?
分析:直接带公式
解:S=3.14×2?
变式1:光盘的银色部分是一个圆环,内圆半径是2cm,外圆半径是6cm。外圆的面积是多少?
解:s=3.14×6?
变式2:光盘的银色部分是一个圆环,内圆半径是2cm,外圆半径是6cm。圆环的面积是多少?
解:方法一: 3.14×6?-3.14×2?
=113.04-12.56
=100.48(cm?)
方法二:3.14×(6?-2?)
=3.14×32
=100.48(cm?)
例4:公园里有一棵大树,同学们用一根20米长的绳子围绕这棵树绕了6圈,还剩下1.16米,求树干的直径是多少?
分析:6圈其实就是树周长的6倍,由此建立等式:
解:(20-1.16)÷6÷3.14
=1m
变式1:公园里有一棵大树,同学们用一根20米长的绳子围绕这棵树绕了几圈,还剩下1.16米,树干的直径是1m,求大家绕了多少圈?
解:(20-1.16)÷1÷3.14
=6圈
变式2:公园里有一棵大树,同学们用一根长的绳子围绕这棵树绕了6圈,还剩下1.16米,树干的直径是1m,求绳子有多少米?
解:3.14×1×6+1.16=20米
例5:一个运动场如右图所示,两端是半圆形,中间是长方形。
小海在运动场上跑2圈,一共跑了多少米?
分析:操场周长可以看成一个圆周加上一个长方形的两个长。
解:L=(100+100+3.14×60)×2
=388.4×2
=776.8m
变式1:一个运动场如右图所示,两端是半圆形,中间是长方形。小海在运动场上跑了776.8米,一共跑了多少圈?
解:(776.8÷2-200)÷3.14÷60=2圈
变式2:一个运动场如右图所示,两端是半圆形,中间是长方形。小海和小明在运动场上同向而跑,6分钟时,小海跑2圈而小明跑了2圈半,问他们的速度差?
解:L1=(100+100+3.14×60)×2
=388.4×2
=776.8m
L2=(100+100+3.14×60)×2.5
=388.4×2.5
=971m
小海的速度:776.8÷6=129.47m/min
小明的速度:971÷6=161.83m/min
速度差:161.83-129.47=32.36m/min
课堂总结
在圆一个小节,要注意审题,看清楚是直径还是半径,牢记公式,认真书写。
四、课后作业
1. 一个圆形茶几桌面的直径是1m,它的面积是多少平方米?
1÷2=0.5(m)
3.14×0.5?=0.785(m?)
答:它的面积是0.785m?。先求出半径,再求圆的面积。
2. 一个圆形环岛的直径是50m,中间是一个直径为10m的圆形花坛,其他地方是草坪。草坪的占地面积是多少?
3.14×(25?-5?)
=3.14×600
=1884(m?)
要求草坪的占地面积,也就是求圆环的面积。
3.看图求出阴影部分的面积。(单位:厘米)
10
15
6
6
解:
s=6×6-3.14×6×6÷4=7.74平方厘米
S=3.14×15×15-3.14×10×10=392.5平方厘米
4.为美化校园,学校在教学楼前修了一个周长是31.4m的圆形花坛,围绕花坛铺了一条2m宽的环形小路。这条小路的面积是多少平方米?
解:31.4÷3.14÷2=5m
S=3.14×(5+2)×(5+2)-3.14×5×5=75.36平方米
5.一个圆和一个正方形,它们的周长相等,它们的面积相比较是( )。
A.圆的面积大 B.正方形的面积大 C. 面积同样大
6.如果两个圆的半径之比是2:3,那么这两个圆的面积之比是( )
A.2:3 B.3:2 C.4:9
7.车轮滚动一周,求所行驶的路程就是求车轮的( )。
A.直径 B.周长 C. 面积
答案:ACB
附:
单位换算
熟记基本换算关系: 高级单位化低级单位:×进率 低级单位聚高级单位:÷进率
(长度单位):1千米=1000米????1米=10分米 1分米=10厘米
1厘米=10毫米 1米=100厘米??? ?? 1米=1000毫米
(面积单位):1平方千米=100公顷 1公顷=10000平方米
1平方米=100平方分米 1平方分米=100平方厘米
1平方厘米=100平方毫米
第四-五讲 平面图形的特征及计算-学生版
三角形
一、知识梳理
由三条线段围成的图形(每相邻两条线段的端点相连)叫做三角形。
(1)特征
三角形都有三条边、三个顶点、三个角;
三角形内角和是180度。
从三角形的一个顶点到它的对边做一条垂线,顶点和垂足之间的线段叫三角形的高,这条对边叫做三角形的底。三角形有三条高。
三角形具有稳定性。
(2)计算公式
三角形面积:三角形面积=底×高÷2
用字母表示:
s=ah/2
(3) 分类
按角分
锐角三角形 :三个角都是锐角。
直角三角形 :有一个角是直角。等腰三角形的两个锐角各为45度,它有一条对称轴。
钝角三角形:有一个角是钝角。
按边分
不等边三角形:三条边长度不相等。
等腰三角形:有两条边长度相等;两个底角相等;有一条对称轴。
等边三角形:三条边长度都相等;三个内角都是60度;有三条对称轴。
二、例题精讲
例1:求下列三角形的面积。(单位m)
15
12
15
15
12
10
解析:直接带入三角形的面积公式:s=ah/2
解1:s=10×12÷2=120÷2=60
2:s=15×15÷2=225÷2=112.5
3:s=12×15÷2=180÷2=90
总结:计算三角形面积的时候,找准底和高,直接带入公式。
变式1:如图:求三角形的面积:
分析:本题要找准三角形的高是谁,底是谁,要知道底和高的垂直关系则可以找到底是4cm,高是3cm。带入公式
解:s=ah÷2=3×4÷2=6
变式2:已知等腰三角形的底边上的高是8cm,底边是高的1.5倍,求三角形的面积。
解:s=ah÷2=8×8×1.5÷2=48
8
6
例2:把大、小两个正方形拼在一起,它们的边长分别是8米和6米,那么图中阴影部分的面积是多少平方米?
分析:本题首先要找准底和高。然后直接带公式。
解:s=ah/2=(8-6)×6÷2=6
变式1:如图,求图中阴影部分的面积是多少平方米?
10
7
解:s=ah/2=(10-7)×7÷2=10.5
变式2:如图:求图中阴影部分的面积是多少平方米?
6
8
解:s=ah/2=6×6÷2=18
例3:如图,平行四边形ABCD的面积是32平方厘米,三角形CED是一个直角三角形,已知AE=5厘米,CE=4厘米,那么阴影部分的面积是多少平方厘米?E
A
B
C
D
分析:可以把平行四边形分成一个矩形和2个相等的三角形,用总面积减去矩形的面积除以2即可:
解:s=(32-5×4)÷2
=12÷2
=6(平方厘米)
变式1:如上图:若四边形ABCE的面积是26平方厘米,AE=5厘米,CE=4厘米,那么阴影部分的面积是多少平方厘米?
解:s=26-5×4
=26-20
=6(平方厘米)
变式2:在上题中,已知平行四边形ABCD的面积是32平方厘米,无其余条件,则阴影三角形的面积最大是多少?
解:S=32÷2=16(平方厘米)
例4:如图,在平行四边形ABCD中,三角形BCE的面积是42平方厘米,BC的长度为14厘米,AE的长度为9厘米,三角形ECD的面积又是多少平方厘米?
A
B
C
D
E
分析:知道三角形BCE的面积和BC的长度,则可以求高,AE=9,求得ED=5,则可以直接带公式。
解:s=42x2÷14x(14-9)÷2
=15(平方厘米)
变式1:如上图,三角形ECD的面积是15平方厘米,BC的长度为14厘米,AE的长度为9厘米,三角形BCE的面积又是多少平方厘米?
解:三角形的高h=14x2÷(14-9)=6cm
S=14x6÷2=42(平方厘米)
变式2:如上图,若有一平行四边形菜地,总面积是42平方米,共收获420kg白菜,则三角形ECD菜地大约收获多少白菜?
分析:收获的菜与其面积成正比,面积越大则收获的越多。
解s=42x2÷14x(14-9)÷2
=15(平方米)
收获白菜:420÷42x15=150kg
例5:每个小方格的边长表示1CM,三角形的面积是多少?
分析:由图可以看出,三角形的底边是7,高是4带入公式
S=7×4÷2=14(平方厘米)
变式1:如下图,每个小方格的边长表示1CM,三角形的面积是多少?
解:s=2×3÷2=3(平方厘米)
变式2:如下图,每相邻三个点所形成的三角形都是面积为1的等边三角形,计算△ABC的面积.
分析 这是个三角形,虽然有三角形面积公式可用,但判断它的底和高却十分困难,只能另想别的办法:这个三角形是处在长是6、宽是4的矩形内,除此之外还有其他三个直角三角形,如下图(b),这三个直角三角形面积很容易求出,再用矩形面积减去这三个直角三角形面积,就是所要求的三角形面积.
解:矩形面积是6×4=24.
直角三角形I的面积是:
6×2÷2=6.
直角三角形Ⅱ的面积是:4×2÷2=4,
直角三角形Ⅲ的面积是:4×2÷2=4.
所求三角形的面积是:
24-(6+4+4)=10
三、课堂总结
找准三角形的各边,牢记公式,灵活运用上解决三角形问题的关键和方法。
课后作业
1.比一比下面两个图形的面积。结果是( )。
① ② A.①>②
B. ①<②
C. ①=②
答案C
2.若图中涂色部分代表240元,则全部代表多少钱?
分析,可以算出一个小三角形代表多少,则可以算出全部
解:240÷4×9=540元
3.如图ABFE和CDEF都是长方形,AB的长是4厘米,BC的长是3厘米,那么图中阴影部分的面积是多少平方厘米?
分析:根据三角形等底等高的性质,可以得出阴影部分的面积和空白一样。
解:s=4×3÷2=6(平方厘米)
4.一块正方形菜地,边长20m,平均分成两块三角形菜地,其中一块种白菜,另一块种菠菜,已知每平方米可以收获白菜10kg,菠菜6kg,问这块地收获白菜菠菜个多少千克?
解:三角形的面积s=20×20÷2=200(平方米)
收获白菜:200x10=2000kg
收获菠菜:200x6=1200kg
5.已知三角形ABC的面积为1,BE=2AB,BC=CD,求三角形BDE的面积?(下页图)
分析,见右图,连结CE.对于三角形ABC与三角形BEC,分别把AB和BE可知,S△BEC=2S△ABC=2.显然,三角形BEC和三角形CED是两个等底(BC=CD)、等高的三角形,因此 S△CED=S△BEC=2。 这样,S△BDE=S△BEC+S△CED=4。
长方形
一、知识梳理
四个角都是直角的平行四边形叫做长方形
(1)特征
长方形有四条边,对边相等,4个角都是直角的四边形。
长方形长边的长叫作长,短边的长叫宽。
长方形是轴对称图形,它有两条对称轴。
(2)计算公式
周长=(长+宽)×2
字母表示为:
c=2(a+b)
面积=长×宽
字母表示为:
s=ab
二、例题精讲
例1:求长方形的周长和面积
35cm
20cm
5dm
12dm
分析:对于单一的题目,直接带公式:
c=(35+20)×2=55x2=110cm s=35x20=700
30厘米
21厘米
C=(5+12)x2=17x2=34dm s=5x12=60
例2:一张长方形的A4纸(如下图),它的面积是多少
平方厘米?
30×21=630(平方厘米)
变式1:如果从这张纸上剪下一个最大的正方形,
这个正方形的面积是多少?
21×21=441(平方厘米)
变式2:如果从这张纸上剪下一个最大的正方形,剩下的面积是多少?
630-441=169(平方厘米)
例3:小红用一根长 8 厘米的铁丝,围成一个最大的正方形,这个正方形的边长是多少?面积是多少?
分析,要正方形最大,则48即周长,根据公式计算边长,然后计算面积。
解:8÷4=2厘米
2×2=4平方厘米
变式1:小红用一根长铁丝围成一个正方形,这个正方形的面积是16平方厘米。它的周长是多少?边长是多少?
解:16=4×4,所以边长是4厘米
C=4×4=16厘米
变式2:小红用n个长3厘米,宽x厘米的长方形拼车一个正方形,正方形的周长12厘米,求整数x和n?
解:12÷4=3 所以边长为3,长大于宽,所以x=1或者x=2
1)若x=1,则n=3
2)若x=2,则n=2
花圃
例4:小区前面有一块60米边长的正方形空坪,现要在空坪的中间做一个长32米、宽28米的长方形花圃,其余的植上草皮.(如下图)
花圃的面积是多少平方米?草皮的面积是多少平方米?
解:花圃:32×28=896平方米
草皮:60×60-896=2704平方米
变式1:小区前面有一块长60米,宽40米的长方形草地,现在修一条平行于长的长方形小路,宽2m,问草地面积还有多少?
解:
S=(40-2)×60=2280平方米
变式2:小区前面有一块长60米,宽40米的长方形草地,现在修两条分别平行于长和宽的长方形小路,小路宽2m,问草地面积还有多少?
解:
S=(60-2)×(40-2)=2204平方米
例5:一块广告牌长6米,宽2米,如果每平方米用油漆2千克,这块广告牌一共要用多少千克油漆?
分析:知道每平方米用油漆2千克,只要算出有多少面积即可
解:S=6×2=12平方米
12×2=24千克
变式1:一间长方形会议室长12米,宽6米。这个会议室地板面积是多少平方米?合多少平方分米?如果一块地砖的面积是9平方分米,铺完这间会议室地板至少要用多少块这样的地砖?
解:12×6=72平方米=7200平方分米
7200÷9=800块
变式2:一间长方形会议室长12米,宽6米。这个会议室地板面积是多少平方米?合多少平方分米?如果一块正方形地砖的边长是3分米,铺完这间会议室地板至少要用多少块这样的地砖?
解:12×6=72平方米=7200平方分米
36×3=9平方分米
7200÷9=800块
三、课堂总结
在解决长方形问题的时候要抓住其特征进行条件查找,在记住公式的同时灵活运用在解题上面。
四、课后作业
一块长方形菜地,长20米,宽8米。如果要给这块菜地围上篱笆,篱笆的长是多少米?
答案:(20+8)×2=56m
9
4
5
5
7
2
2.计算下面图形的面积。
9×4=36(平方厘米) 5×5=25(平方厘米)
有一个长方形田地。长是600米,宽是300米,面积是多少公顷?如果围上篱笆,篱笆的长是多少米?如果每公顷收白菜150吨,可以收白菜多少吨?
答案:s=600×300=180000平方米=18公顷
C=(600+300)×2=1800米
18×150=2700吨
4.一个零件形状如图,计算它的周长和面积。(单位:厘米)
6
14
14
6
答案:整体看
s=14×14-6×6=108平方厘米
C=14×4=56厘米
5.一洒水车,每分钟行驶200米,洒水的宽度是10米,洒水车行驶6分钟,能给多大的地面洒上水?
答案:6×200×10=12000平方米
正方形
一、知识梳理
长和宽相等的长方形是正方形。
(1)特征:
四条边都相等,四个角都是直角的四边形。
正方形每条边的长叫作边长。
正方形是轴对称图形,它有4条对称轴。正方形还是中心对称图形。
(2)计算公式
周长=边长x4
用字母表示:
c=4a
面积=边长x边长
用字母表示:
s=a × a=
二、例题精讲
例1:
边长:16米 边长:300厘米
面积:16×16=256平方米 面积:300×300=90000平方厘米
周长:16×4=64米 周长:300×4=1200厘米
例2:把一个长10厘米,宽3厘米的长方形硬纸剪成面积尽可能大的正方形,可以剪( )。
A.1个 B.2个 C.3个
分析,长方形的长是宽的3倍还多1,所以可以剪3个
选C
变式1:5个边长1m的正方形拼在一起构成一个长方形,周长是多少?
C=(5+1)×2=12m
变式2: 用6个边长1m的正方形拼在一起构成一个长方形,周长是多少?
分析:6个正方形可以分2排或者1排,所以有两种情况
c=(6+1)×2=14m
C=(2+3)×2=10m
例3:用边长1厘米的小正方形拼成图形 ,它的周长是( ),面积是( )。
分析:图形可以通过移动边使其变成一个长方形c=(2+3)×2=10。面积没有变化
答案:10厘米,4平方厘米
变式1:用边长1厘米的小正方形拼成图形,它的周长是( ),面积是( )。
C=(2+5)×2-1=13厘米
S=5+2=7平方厘米
变式2:用边长1厘米的小正方形拼成图形,它的周长是( ),面积是( )。
解:
C=(3+5)×2=16厘米
S=3+3+5=11平方厘米
例4:小明家的客厅长5米,宽4米。地面上铺有边长为5分米的正方形地砖。铺这个客厅,需要多少块地砖?
分析:先换算单位,根据面积相等计算
解:5米=50分米 4米=40分米
50×40÷(5×5)
=2000÷25
=80(块)
变式1:小明家的客厅长5米,宽4米。地面上铺有边长为5分米的正方形地砖,这种地砖20元一块。铺这个客厅,需要多少块地砖?买这些地砖共需多少钱?
由上题可以知道需要80块
解:
总钱=80×20=1600元
变式2:小明家的客厅长5米,宽4米。地面上铺有边长为5分米的正方形地砖,铺这个客厅,买这些地砖共需1600元。这种地砖多少元一块?
计算单价,有总价除以块数
解:
1600÷80=20元
例5:小红用一根长 48 厘米的铁丝,围成一个最大的正方形,这个正方形的边长是多少?面积是多少?
分析,要正方形最大,则48即周长,根据公式计算边长,然后计算面积。
解:48÷4=12厘米
12×12=144平方厘米
变式1:小红用一根长铁丝围成一个正方形,这个正方形的面积是144平方厘米。它的周长是多少?边长是多少?
解:144=12×12,所以边长是12厘米
C=12×4=48厘米
变式2:小红用3个长3厘米,宽2厘米的长方形拼车一个正方形,求正方形的周长和面积?
解:c=3×4=12厘米
S=3×2×3=18平方厘米
三、课堂总结
解决正方形问题的时候要抓住其特征进行条件查找,灵活运用。
四、课后作业
1.求下面长方形的周长和面积:(单位:厘米)
5 4
1
周长:12厘米 周长:16厘米
面积: 5平方厘米 面积:16平方厘米
6
6
6×6=36(平方厘)米)
9×2=18(平方厘)米)
9
2
7
8×7=56(平方厘米)
2.求下图的面积
3.用18个边长为1厘米的小正方形拼成一个长方形,要使长方形的周长最大应怎样拼?周长最小呢?请画出图,并列式计算。
解
要是周长最大,则需要一字排开
C=(1+18)×2=38cm
要是周长最小,则需要尽可能的靠拢:如图
C=(3+6)×2=18cm
4.足球场是一个长方形,长 100 米,宽 75 米,小明沿着足球场跑了 2 圈,跑了多少米?
解:c=(100+75)×2=350m
一块长方形菜地,长6米,宽4米。四周围上篱笆,篱笆长多少米?如果一面靠墙,篱笆至少要多少米?
答案:20m,14m
平行四边形
一、知识梳理
有两组对边分别平行的四边形是平行四边形。
(1) 特征
相对的边平行且相等。对角相等,相邻的两个角的度数之和为180度。平行四边形容易变形。
(2) 计算公式
平行四边形的面积=底×高
用字母表示:
s=ah
二、例题精讲
例1:右图中有( )个平行四边形,
答案:3
变式1:下图中有( )个平行四边形
答案:9
变式2:下图中有( )个平行四边形
答案:13
例2:计算下面各个平行四边的面积。(单位:m)
S1=2.8×1.2=3.36平方米
S2=1.6×0.8=1.28平方米
例3: 一平行四边形的底27厘米,高12.5厘米;另一条底18厘米,这条底边上的高是多少厘米?
分析,根据面积相等即可求得。
27×12.5=337.5(厘米2)
337.5÷18=18.75(厘米)
答:这条底边上的高是18.75厘米。
变式1:一平行四边形的底24厘米,高是底的一半;另一条底18厘米,这条底边上的高是多少厘米?
24×24÷2÷18=16厘米
变式2:一平行四边形的面积是18平方厘米,高是底的一半;另一条底是前一条底的一半,另一条底边上的高是多少厘米?
18÷2=9 9=3×3
所以,底是3厘米,高6厘米
6×2=12厘米
答:另一条底边上的高是12厘米.
例4:把一个长方形拉成平行四边形后,它的面积( )
A比原来大 C比原来小
B与原来相等 D无法确定
分析,长方形边长平行四边形后,高变小,所以选C
变式1:把一个平行四边形拉成长方形后,它的面积( )
A比原来大 C比原来小
B与原来相等 D无法确定
分析,长方形边长平行四边形后,高变小,反之选A
变式2:把一个长方形拉成平行四边形后,它的面积变成原来的一半,则高怎么变化
答:高变为原来的一半
例5:如图,两个边长10厘米的正方形相互错开3厘米,那么图中阴影平行四边形的面积是多少?
分析:阴影部分的面积等于总面积减去四个小三角形的面积。
S=10×10×2-10×10-3×3
=91平方厘米
变式1:上题中,当正方形错开5厘米时,阴影面积是多少?
S=10×10×2-10×10-5×5
=75平方厘米
变式2:上题中,当正方形大约错开多少厘米时,阴影面积是总面积的四分之一?
由题意得:50=10×10×2-10×10-n×n
n≈7cm
课堂总结
图形面积的计算属于较简单的问题,找准数量关系是解题的关键。
四、课后作业
1.已知下图中正方形的周长是36厘米,求平行四边形的面积。
36÷4=9(厘米)
9×9=81(平方厘米)
2.平行四边形的面积是36.8平方分米,高是2.3分米,底是多少?
a = s÷h
= 36.8÷2.3
= 16(分米)
答:底是16分米。
3.一块平行四边形的菜地,底是30米,高是21米。如果每棵大白菜占地9平方分米,这块地一共可种多少棵大白菜?
30×21=630(平方米)
630平方米=63000平方分米
63000÷9=7000(棵)
答:这块地一共可种7000棵大白菜。
4.一块平行四边形的铁皮的周长是82厘米,一条底长是16厘米,这条底上的高是20厘米,求另一条底上的高是多少厘米?
82÷2-16=25(厘米)
16×20÷25=12.8(厘米)
5.如右图,四边形ABCD和DEFG都是平行四边形,证明它们的面积相等
证明:连结CE,平行四边形ABCD的面积等于△CDE面积的2倍,而平行四边形DEFG的面积也是△CDE面积的2倍。
∴平行四边形ABCD的面积与平行四边形DEFG的面积相等。
梯形
一、知识梳理
梯形:指一组对边平行而另一组对边不平行的四边形叫做梯形。
上底
①上底、下底:平行的两边叫做梯形的底边,其中长边叫下底,短边叫上底;
高
②腰:不平行的两边叫腰;
③高:夹在两底之间的垂线段叫梯形的高。
下底
(1)特征
只有一组对边平行的四边形。
中位线等于上下底和的一半。
两腰相等的梯形是等腰梯形,等腰梯形有一条对称轴。
(2) 公式
梯形的面积:(上底+下底)×高÷2
用字母表示:
s=(a+b)h/2
二、例题精讲
20
32
20
例1:计算下面各梯形的面积。(单位:厘米)X k
分析:直接带入公式
解:
(15+20)×8÷2 =140(平方厘米)
(20+32)×20÷2 =520(平方厘米)
例2:有一块梯形花地,上底是8米,下底是10米,高是4.8米。已知每株花占地0.06平方米,这块地能种花多少株?
分析:先计算面积,然后计算株数。
解:(8+10)×4.8÷2÷0.06=720(株)
变式1:有一块梯形花地,上底是8米,下底是10米,高是4.8米。已知,这块地能种花720株,每株花占地多少平方米?
解:(8+10)×4.8÷2÷720=0.06(平方米)
变式2:有一块梯形花地,上底是8米,下底是10米。已知,这块地能种花720株且每株花占地0.06平方米,问高是多少米?
解:设高是h:
(8+10)×h÷2÷720=0.06
解得h=4.8m
例3:一个梯形的上底是12分米,高是8分米,面积是108平方分米。这个梯形的下底是多上分米?
分析:根据面积公式求解。
解:108×2÷8-12=15(分米)
变式1:一个梯形的上底是12分米,下底是15分米,面积是108平方分米。这个梯形的高是多少分米?
解:h=108×2÷(12+15)
=8dm
变式2:一个梯形的上底是12分米,下底是上底的2倍,面积是108平方分米。这个梯形的高是多少分米?
解:h=108×2÷(12+12×2)
=6dm
例4:已知梯形的面积是20平方分米,求阴影部分的面积。
3.2分米
解:20×2÷(3.2+6.8)=4(分米)
变式1:如图所示,大正方形的边长是12米,小正方形的边长是5米,求阴影部分的面积。
w W w . x K b 1.c o M
解:(5+12)×12÷2=102(平方米)
变式2:图中,阴影部分的面积是13.5平方厘米,着个梯形的面积是多少?
7厘米
解:13.5×2÷9=3(厘米)
(7+9)×3÷2=24(平方厘米)
例5:用篱笆围城一个梯形养鸡场,一边利用房屋的墙壁,篱笆的 长是65米,求养鸡长得面积。
X k B 1 . c o m
15米
解:(65-15)×15÷2=375(平方米)
变式1:上题中,若上底是下底的3倍,则上底是多少?
(65-15)÷(1+3)=10m
变式2:如下图,若梯形上底是下底的3倍,面积是300平方米,则高是多少?
15米
解:h=300×2÷(15+15×3)
=10m
课堂总结
牢记梯形的面积公式。熟练运用。
四、课后作业
1、可以把一个梯形分成两个( )形,也可以分成一个( )形和一个( )形。
2、梯形的上底长8厘米,下底长14厘米,高是上底的一半。梯形的面积是( )平方厘米。
3、两个完全一样的梯形拼成的一个平行四边形的面积是80平方厘米,高是5厘米,梯形的上底是7厘米,梯形的下底是( )厘米。
4、一个梯形上下底的和是16米,高是7米,它的面积是( )
5、判断下列各题,对的打√,错的打×
(1)两个面积一样的梯形一定可以拼成一个平行四边形 ( )
(2)平行四边形的面积是梯形面积的两倍( )
(3)计算一个梯形的面积,比武知道他的上下底和高 ( )
(4)一个梯形两底的和是12米,高是10米,则它的面积是60平方米 ( )
答案:1.三角形, 三角形, 平行四边形 2. 44 3. 9 4. 56 5.××√√
5.如图,梯形ABCD的面积是45平方米,高6米,△AED的面积是5平方米,BC=10米,求阴影部分面积.
解:∵梯形面积=(上底+下底)×高÷2
即45=(AD+BC)×6÷2,
45=(AD+10)×6÷2,
∴AD=45×2÷6-10=5米。
∴△ADE的高是2米。
△EBC的高等于梯形的高减去△ADE的高,
即6-2=4米,
S=BC×4÷2=20平方米
圆
一、知识梳理
(1)圆
到定点的距离等于定长的所有点组成的图形。
圆中心的一点叫做圆心。一般用字母o表示。
半径:连接圆心和圆上任意一点的线段叫做半径。一般用r表示。
在同一个圆里,有无数条半径,每条半径的长度都相等。
通过圆心并且两端都在圆上的线段叫做直径。一般用d表示。
同一个圆里有无数条直径,所有的直径都相等。
同一个圆里,直径等于两个半径的长度,即d=2r。
圆的大小由半径决定。 圆有无数条对称轴。
(2)圆的画法
把圆规的两脚分开,定好两脚间的距离(即半径);
把有针尖的一只脚固定在一点(即圆心)上;
把装有铅笔尖的一只脚旋转一周,就画出一个圆。
(3) 圆的周长
围成圆的曲线的长叫做圆的周长。
把圆的周长和直径的比值叫做圆周率。用字母∏表示。
(4) 圆的面积
圆所占平面的大小叫做圆的面积。
(5)计算公式
d=2r
r=d/2
c=∏d
c=2∏r
s=∏r?
二、例题精讲
例1:求下列圆的周长及面积。
(半径3) (直径12)
周长:2×3.14×3=18.84 周长:3.14×12=37.68
面积:3.14×3×3=28.26面积:3.14×(12÷2)×(12÷2)=113.04
例2:圆形草坪的半径是10m,每平方米草皮8元,铺满需要多少钱?
分析:先求出面积,即可求得钱数。
解3.14×10×10=314平方米
314×8=2512元
变式1:圆形草坪的直径是20m,每平方米草皮8元,铺满需要多少钱?
解:20÷2=10米
3.14×10×10=314平方米
314×8=2512元
变式2:圆形草坪的直径是20m,铺满需要钱2512元,每平方米草皮多少元?
解:20÷2=10米
3.14×10×10=314平方米
2512÷314=8元
例3:光盘的银色部分是一个圆环,内圆半径是2cm,外圆半径是6cm。内圆的面积是多少?
分析:直接带公式
解:S=3.14×2?
变式1:光盘的银色部分是一个圆环,内圆半径是2cm,外圆半径是6cm。外圆的面积是多少?
解:s=3.14×6?
变式2:光盘的银色部分是一个圆环,内圆半径是2cm,外圆半径是6cm。圆环的面积是多少?
解:方法一: 3.14×6?-3.14×2?
=113.04-12.56
=100.48(cm?)
方法二:3.14×(6?-2?)
=3.14×32
=100.48(cm?)
例4:公园里有一棵大树,同学们用一根20米长的绳子围绕这棵树绕了6圈,还剩下1.16米,求树干的直径是多少?
分析:6圈其实就是树周长的6倍,由此建立等式:
解:(20-1.16)÷6÷3.14
=1m
变式1:公园里有一棵大树,同学们用一根20米长的绳子围绕这棵树绕了几圈,还剩下1.16米,树干的直径是1m,求大家绕了多少圈?
解:(20-1.16)÷1÷3.14
=6圈
变式2:公园里有一棵大树,同学们用一根长的绳子围绕这棵树绕了6圈,还剩下1.16米,树干的直径是1m,求绳子有多少米?
解:3.14×1×6+1.16=20米
例5:一个运动场如右图所示,两端是半圆形,中间是长方形。
小海在运动场上跑2圈,一共跑了多少米?
分析:操场周长可以看成一个圆周加上一个长方形的两个长。
解:L=(100+100+3.14×60)×2
=388.4×2
=776.8m
变式1:一个运动场如右图所示,两端是半圆形,中间是长方形。小海在运动场上跑了776.8米,一共跑了多少圈?
解:(776.8÷2-200)÷3.14÷60=2圈
变式2:一个运动场如右图所示,两端是半圆形,中间是长方形。小海和小明在运动场上同向而跑,6分钟时,小海跑2圈而小明跑了2圈半,问他们的速度差?
解:L1=(100+100+3.14×60)×2
=388.4×2
=776.8m
L2=(100+100+3.14×60)×2.5
=388.4×2.5
=971m
小海的速度:776.8÷6=129.47m/min
小明的速度:971÷6=161.83m/min
速度差:161.83-129.47=32.36m/min
课堂总结
在圆一个小节,要注意审题,看清楚是直径还是半径,牢记公式,认真书写。
四、课后作业
1. 一个圆形茶几桌面的直径是1m,它的面积是多少平方米?
2. 一个圆形环岛的直径是50m,中间是一个直径为10m的圆形花坛,其他地方是草坪。草坪的占地面积是多少?
3.看图求出阴影部分的面积。(单位:厘米)
10
15
6
6
4.为美化校园,学校在教学楼前修了一个周长是31.4m的圆形花坛,围绕花坛铺了一条2m宽的环形小路。这条小路的面积是多少平方米?
5.一个圆和一个正方形,它们的周长相等,它们的面积相比较是( )。
A.圆的面积大 B.正方形的面积大 C. 面积同样大
6.如果两个圆的半径之比是2:3,那么这两个圆的面积之比是( )
A.2:3 B.3:2 C.4:9
7.车轮滚动一周,求所行驶的路程就是求车轮的( )。
A.直径 B.周长 C. 面积
附:
单位换算
熟记基本换算关系: 高级单位化低级单位:×进率 低级单位聚高级单位:÷进率
(长度单位):1千米=1000米????1米=10分米 1分米=10厘米
1厘米=10毫米 1米=100厘米??? ?? 1米=1000毫米
(面积单位):1平方千米=100公顷 1公顷=10000平方米
1平方米=100平方分米 1平方分米=100平方厘米
1平方厘米=100平方毫米
同课章节目录
