2011-2012学年第一学期期末检测九年级数学试题(有答案)
文档属性
| 名称 | 2011-2012学年第一学期期末检测九年级数学试题(有答案) |  | |
| 格式 | zip | ||
| 文件大小 | 120.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-03-30 09:30:14 | ||
图片预览



文档简介
2011-2012学年第一学期期末检测
九年级数学试题
分值:120分 时间:120分钟 命题人:蒋丽娜
第Ⅰ卷(共36分)
一、选择题(本题共12个小题,每小题3分,共36分)
1、下列图形中既是轴对称图形又是中心对称图形的是( )
2、函数中自变量x的取值范围是( )
A.≥-3 B.≥-3且 C. D.且
3、如图,下列条件之一能使平行四边形ABCD是菱形的为( )
① ② ③ ④
A.①③ B.②③ C.③④ D.①②③
4、如图,在长为、宽为的矩形中,截去一个矩形,使得留下的矩形(图中阴影部分)与原矩形相似,则留下矩形的面积是( )
A. B. C. D.
5、已知关于x的方程x 2+bx+a=0有一个根是-a(a≠0),
则a-b的值为( )
A.-1 B.0 C.1 D.2
6、已知:如图,AB、AC分别切⊙O于B、C,D是⊙O上一点,∠D=400,
则∠A的度数等于( )
A.1400 B.1200 C.1000 D.800
7、如图所示,函数和的图象相交于(-1,1)
(2,2)两点.当时,x的取值范围是( )
A.x<-1 B.—1<x<2 C.x>2 D. x<-1或x>2
8、直角三角板ABC的斜边AB=12㎝,∠A=30°,将三角板ABC绕C顺时针旋转90°至三角板的位置后,再沿CB方向向左平移,使点落在原三角板ABC的斜边AB上,则三角板平移的距离为( )
A.6㎝ B. 4㎝ C.(6- )㎝ D.()㎝
9、已知抛物线y=ax2+bx+c(a≠0)在平面直角坐标系中的位置如图所示,则下列结论中正确的是( )
A. a>0 B. b<0 C. c<0 D. a+b+c>0 9题图
10、如图,直线和双曲线交于A、B亮点,P是线段AB上的点(不与A、B重合),过点A、B、P分别向x轴作垂线,垂足分别是C、D、E,连接OA、OB、OP,设△AOC面积是S1、△BOD面积是S2、△POE面积是S3、则( )
A.S1<S2<S3 B.S1>S2>S3 C.S1=S2>S3 D.S1=S211、关于x的方程x2+2kx+k﹣1=0的根的情况描述正确的是( )
A、k为任何实数,方程都没有实数根
B、k为任何实数,方程都有两个不相等的实数拫
C、k为任何实数,方程都有两个相等的实数根
D、根据k的取值不同,方程根的情况分为没有实数根、有两个不相等的实数根和有两个相等的实数根三种
12、将正方体骰子(相对面上的点数分别为 1和 6 、 2 和 5 、 3 和 4 )放置于水平桌面上 ,如图 ① .在图 ② 中,将骰子向右翻滚,然后在桌面上按逆时针方向旋转,则完成一次变换.若骰子的初始位置为图①所示的状态,那么按上述规则连续完成10次变换后,骰子朝上一面的点数是( )
A . 6 B . 5 C . 3 D . 2
第Ⅱ卷(共84分)
二、填空题(每题3分,共15分)
13、.已知关于x的方程x2+3x+k2=0的一个根是-1,则k=___ ____.
14、将二次函数y=x2-4x+5化为y=(x-h)2+k的形式y= .
15、在半径为1的⊙O中,弦AB、AC分别是,则∠BAC的度数为_________
16、若点A(m,﹣2)在反比例函数的图象上,则当函数值y≥﹣2时,自变量x的取值范围是 .
17、 如图,在Rt△ABC中,∠ACB=90°,AC=BC=1,将Rt△ABC绕A点逆时针旋转30°后得到Rt△ADE,则图中阴影部分的面积是___________.
三、解答题(共69分)
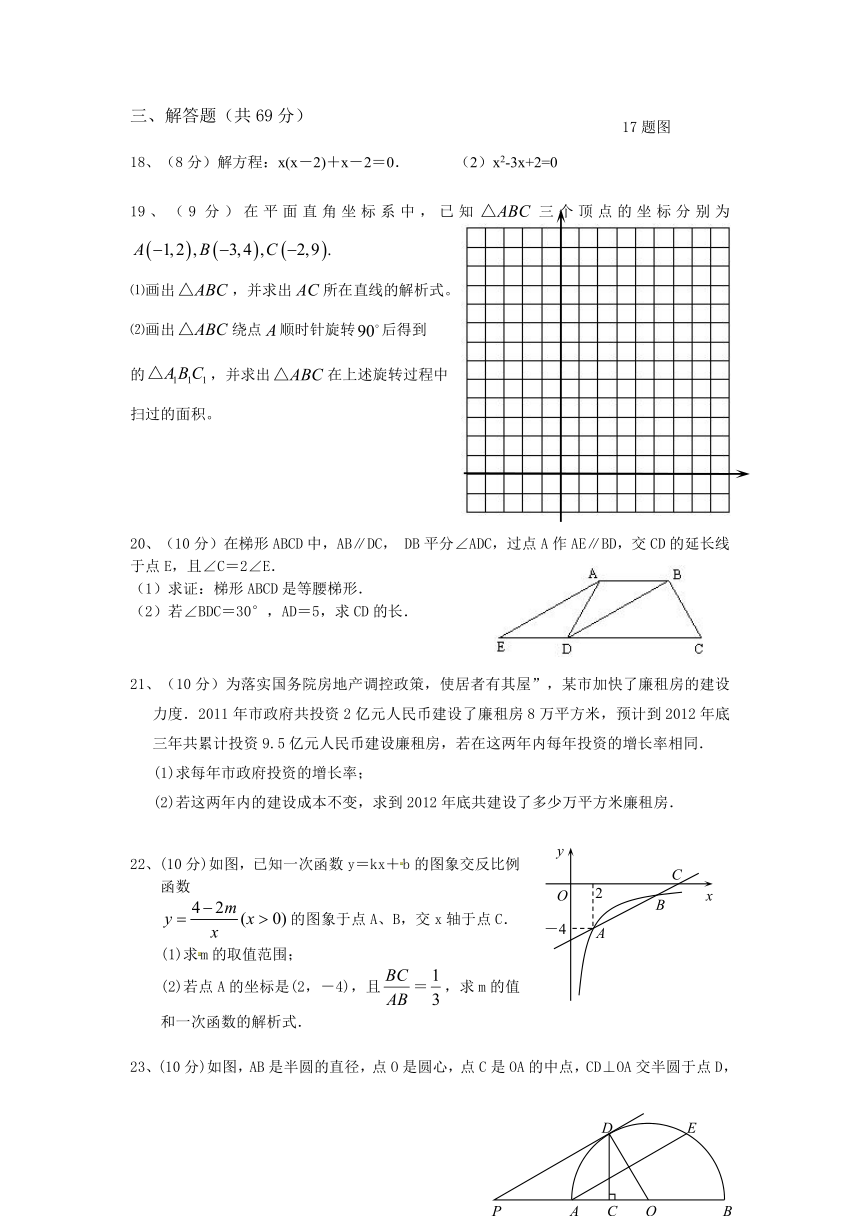
18、(8分)解方程:x(x-2)+x-2=0. (2)x2-3x+2=0
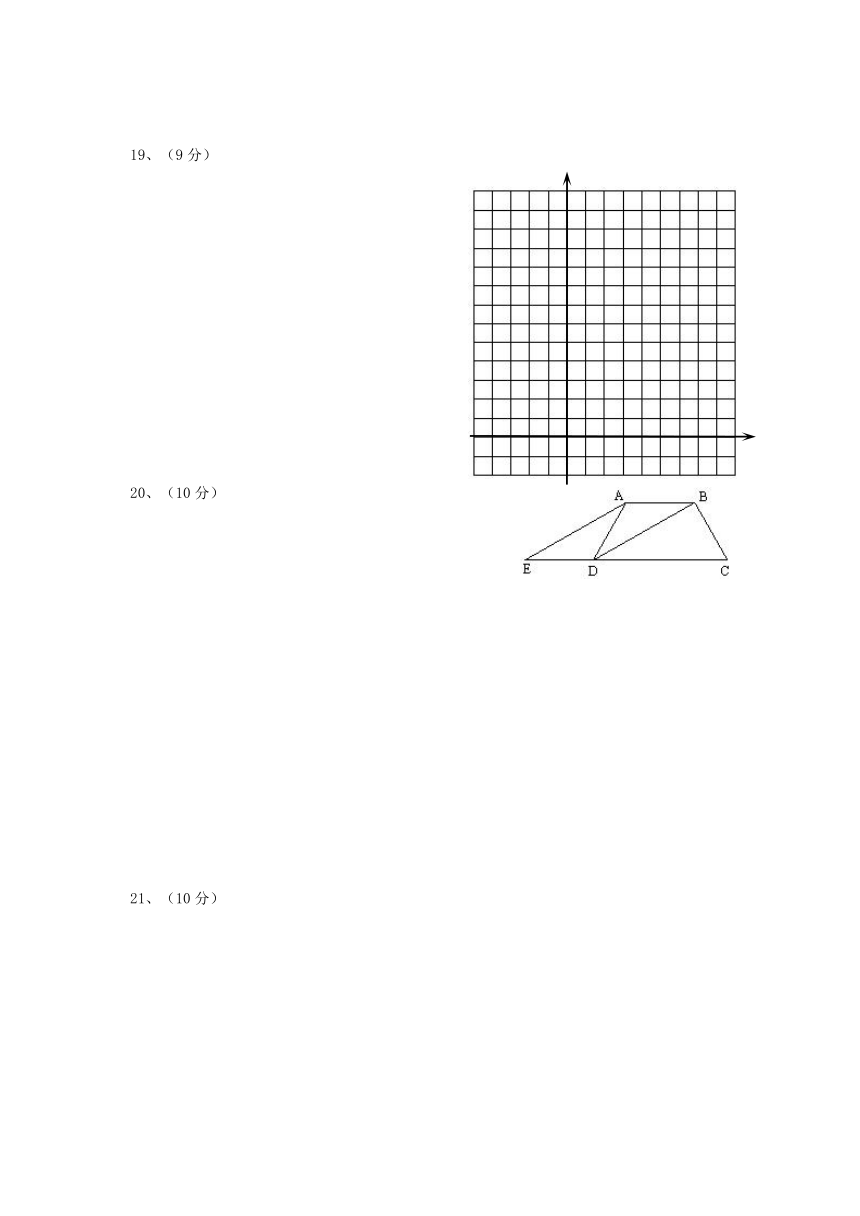
19、(9分)在平面直角坐标系中,已知三个顶点的坐标分别为
⑴画出,并求出所在直线的解析式。
⑵画出绕点顺时针旋转后得到
的,并求出在上述旋转过程中
扫过的面积。
20、(10分)在梯形ABCD中,AB∥DC, DB平分∠ADC,过点A作AE∥BD,交CD的延长线于点E,且∠C=2∠E.
(1)求证:梯形ABCD是等腰梯形.
(2)若∠BDC=30°,AD=5,求CD的长.
21、(10分)为落实国务院房地产调控政策,使居者有其屋”,某市加快了廉租房的建设力度.2011年市政府共投资2亿元人民币建设了廉租房8万平方米,预计到2012年底三年共累计投资9.5亿元人民币建设廉租房,若在这两年内每年投资的增长率相同.
(1)求每年市政府投资的增长率;
(2)若这两年内的建设成本不变,求到2012年底共建设了多少万平方米廉租房.
22、(10分)如图,已知一次函数y=kx+b的图象交反比例函数
的图象于点A、B,交x轴于点C.
(1)求m的取值范围;
(2)若点A的坐标是(2,-4),且=,求m的值和一次函数的解析式.
23、(10分)如图,AB是半圆的直径,点O是圆心,点C是OA的中点,CD⊥OA交半圆于点D,点E是的中点,连接AE、OD,过点D作DP∥AE交BA的延长线于点P.
(1)求∠AOD的度数;
(2)求证:PD是半圆O的切线.
24、(12分)某商场经营某种品牌的童装,购进时的单价是60元.根据市场调查,在一段时间内,销售单价是80元时,销售量是200件,而销售单价每降低1元,就可多售出20件.
(1)写出销售量y件与销售单价x元之间的函数关系式;
(2)写出销售该品牌童装获得的利润w元与销售单价x元之间的函数关系式;
(3)若童装厂规定该品牌童装销售单价不低于76元,且商场要完成不少于240件的销售任务,则商场销售该品牌童装获得的最大利润是多少?
2011-2012学年第一学期期末检测
九年级数学试题
第Ⅱ卷(共84分)
二、填空题(每题3分,共15分)
13. 14. 15.
16. 17.
三、解答题(共69分)
18、(8分)解方程:x(x-2)+x-2=0. (2)x2-3x+2=0
19、(9分)
20、(10分)
21、(10分)
22、(10分)
23、(10分)
24、(12分)
2011-2012学年第一学期期末检测
九年级数学试题
参考答案及评分说明
一、选择题(本题共12个小题,每小题3分,共36分)
题号 1 2 3 4 5 6 7 8 9 10 11 12
答案 B B A C A C D C D D B B
二、填空题(每小题填对得3分,满分15分)
13.± 14.y=(x-2) +1 15. 75°或15° 16.x≤2或x>0 17.π
三、解答题(满分69分)
18.(本题满分8分)
(1)x(x-2)+x-2=0,(因式分解法解)
(x-2)(x+1)=0,
x-2=0,或x+1=0,
x1=2,x2=-1; 4分
(2)x -3x+2=0
(x-2)(x-1)=0
x-2=0或x-1=0
x1=2或x2=1 4分
19.(本题满分8分)
如图所示,即为所求
设所在直线的解析式为
∵,
∴ 解得
∴ ················3分
⑵如图所示,即为所求 ···4分
由图可知, ·········5分
······················6分
=··············9分
20.(本题满分10分)
解
1、∵BD‖AE
∴∠E=∠BDC
∵DB平分∠ADC
∴∠BDC=∠BDA=1/2∠ADC
∵∠C=2∠E
∴∠C=2∠BDC=∠ADC
∴梯形ABCD为等腰梯形 ·····················5分
2、∵∠BDC=30° ∠C=2∠BDC
∴∠C=60°
∴∠CBD=90°
∴△CBD为直角三角形,∠BDC=30°
∴CD=2BC=2AD=2×5=10·····················10分
21.(本题满分10分)
解:(1)设每年市政府投资的增长率为x,
根据题意,得:2+2(1+x)+2(1+x)2=9.5,
整理,得:x2+3x-1.75=0, 解之,得:x=
∴x1=0.5 x2=-0.35(舍去),
答:每年市政府投资的增长率为50%;·····················5分
(2)到2012年底共建廉租房面积=9.5÷(万平方米).·····················10分
22.(本题满分10分)
解:1)由图可以看出:
∵反比例函数y=(4-2m)/x(x>0)图像在第四象限。
∴4-2m<0
∴m>2·····················4分
(2)把A(2,-4)代入
得:
-4=(4-2m)/2
∴m=6
∴反比例函数为:y=-8/x
把A(2,-4)代入y=kx+b,得:
2k+b=-4
∴b=-4-2k
∴一次函数的解析式为:y=kx-4-2k和反比例函数y=-8/x的交点为
-8/x=kx-4-2k
kx -(4+2k)+8=0
(kx-4)(x-2)=0
∴x1=2;x2=4/k
∴B点的坐标是(4/k,-2k)
∵一次函数y=kx+b与x轴的交点C坐标是:((4+2k/k),0)
BC/AB=1/3
BC/AC=1/4
∴ BC的纵坐标之差/AC的纵坐标之差=1:4
即 [0-(-2k)]:[(0-(-4)]=1:4
∴ k=1/2
∴ b=-4-2k=-4+1=-5
∴ 一次函数的解析式为:y=(1/2)x-5 ····················10分
23.(本题满分10分)
(1)∠AOD=60°
(2)第二问切线易证
24.(本题满分12分)
解:(1)根据题意得,y=200+(80-x)×20=-20x+1800,
∴销售量y件与销售单价x元之间的函数关系式为y=-20x+1800;·····················4分
(2)W=(x-60)y=(x-60)(-20x+1800)=-20x2+3000x-108000,
所以销售该品牌童装获得的利润w元与销售单价x元之间的函数关系式y=-20x2+3000x-108000;·····················8分
(3)根据题意得,-20x+1800≥240,x≥76,
∴76≤x≤78,
w=-20x2+3000x-108000,
对称轴为x=- 30002×(-20)=75,
a=-20<0,
∴当76≤x≤78时,W随x的增大而减小,
∴x=76时,W有最大值,最大值=(76-60)(-20×76+1800)=4480(元).
所以商场销售该品牌童装获得的最大利润是4480元.····················12分
说明:解答题各小题只给了一种解答及评分说明,其他解法只要步骤合理、解答正确,均应给出相应分数.
3题图
4题图
6题图
(-1,1)
(2,2)
x
y
O
7题图
10题图
17题图
O
C
B
A
x
y
2
-4
A
P
C
O
B
E
D
O
C
B
A
x
y
2
-4
A
P
C
O
B
E
D
A
B
C
O
B1
C1
A1
x
y
1
1
O
C
B
A
x
y
2
-4
九年级数学试题
分值:120分 时间:120分钟 命题人:蒋丽娜
第Ⅰ卷(共36分)
一、选择题(本题共12个小题,每小题3分,共36分)
1、下列图形中既是轴对称图形又是中心对称图形的是( )
2、函数中自变量x的取值范围是( )
A.≥-3 B.≥-3且 C. D.且
3、如图,下列条件之一能使平行四边形ABCD是菱形的为( )
① ② ③ ④
A.①③ B.②③ C.③④ D.①②③
4、如图,在长为、宽为的矩形中,截去一个矩形,使得留下的矩形(图中阴影部分)与原矩形相似,则留下矩形的面积是( )
A. B. C. D.
5、已知关于x的方程x 2+bx+a=0有一个根是-a(a≠0),
则a-b的值为( )
A.-1 B.0 C.1 D.2
6、已知:如图,AB、AC分别切⊙O于B、C,D是⊙O上一点,∠D=400,
则∠A的度数等于( )
A.1400 B.1200 C.1000 D.800
7、如图所示,函数和的图象相交于(-1,1)
(2,2)两点.当时,x的取值范围是( )
A.x<-1 B.—1<x<2 C.x>2 D. x<-1或x>2
8、直角三角板ABC的斜边AB=12㎝,∠A=30°,将三角板ABC绕C顺时针旋转90°至三角板的位置后,再沿CB方向向左平移,使点落在原三角板ABC的斜边AB上,则三角板平移的距离为( )
A.6㎝ B. 4㎝ C.(6- )㎝ D.()㎝
9、已知抛物线y=ax2+bx+c(a≠0)在平面直角坐标系中的位置如图所示,则下列结论中正确的是( )
A. a>0 B. b<0 C. c<0 D. a+b+c>0 9题图
10、如图,直线和双曲线交于A、B亮点,P是线段AB上的点(不与A、B重合),过点A、B、P分别向x轴作垂线,垂足分别是C、D、E,连接OA、OB、OP,设△AOC面积是S1、△BOD面积是S2、△POE面积是S3、则( )
A.S1<S2<S3 B.S1>S2>S3 C.S1=S2>S3 D.S1=S2
A、k为任何实数,方程都没有实数根
B、k为任何实数,方程都有两个不相等的实数拫
C、k为任何实数,方程都有两个相等的实数根
D、根据k的取值不同,方程根的情况分为没有实数根、有两个不相等的实数根和有两个相等的实数根三种
12、将正方体骰子(相对面上的点数分别为 1和 6 、 2 和 5 、 3 和 4 )放置于水平桌面上 ,如图 ① .在图 ② 中,将骰子向右翻滚,然后在桌面上按逆时针方向旋转,则完成一次变换.若骰子的初始位置为图①所示的状态,那么按上述规则连续完成10次变换后,骰子朝上一面的点数是( )
A . 6 B . 5 C . 3 D . 2
第Ⅱ卷(共84分)
二、填空题(每题3分,共15分)
13、.已知关于x的方程x2+3x+k2=0的一个根是-1,则k=___ ____.
14、将二次函数y=x2-4x+5化为y=(x-h)2+k的形式y= .
15、在半径为1的⊙O中,弦AB、AC分别是,则∠BAC的度数为_________
16、若点A(m,﹣2)在反比例函数的图象上,则当函数值y≥﹣2时,自变量x的取值范围是 .
17、 如图,在Rt△ABC中,∠ACB=90°,AC=BC=1,将Rt△ABC绕A点逆时针旋转30°后得到Rt△ADE,则图中阴影部分的面积是___________.
三、解答题(共69分)
18、(8分)解方程:x(x-2)+x-2=0. (2)x2-3x+2=0
19、(9分)在平面直角坐标系中,已知三个顶点的坐标分别为
⑴画出,并求出所在直线的解析式。
⑵画出绕点顺时针旋转后得到
的,并求出在上述旋转过程中
扫过的面积。
20、(10分)在梯形ABCD中,AB∥DC, DB平分∠ADC,过点A作AE∥BD,交CD的延长线于点E,且∠C=2∠E.
(1)求证:梯形ABCD是等腰梯形.
(2)若∠BDC=30°,AD=5,求CD的长.
21、(10分)为落实国务院房地产调控政策,使居者有其屋”,某市加快了廉租房的建设力度.2011年市政府共投资2亿元人民币建设了廉租房8万平方米,预计到2012年底三年共累计投资9.5亿元人民币建设廉租房,若在这两年内每年投资的增长率相同.
(1)求每年市政府投资的增长率;
(2)若这两年内的建设成本不变,求到2012年底共建设了多少万平方米廉租房.
22、(10分)如图,已知一次函数y=kx+b的图象交反比例函数
的图象于点A、B,交x轴于点C.
(1)求m的取值范围;
(2)若点A的坐标是(2,-4),且=,求m的值和一次函数的解析式.
23、(10分)如图,AB是半圆的直径,点O是圆心,点C是OA的中点,CD⊥OA交半圆于点D,点E是的中点,连接AE、OD,过点D作DP∥AE交BA的延长线于点P.
(1)求∠AOD的度数;
(2)求证:PD是半圆O的切线.
24、(12分)某商场经营某种品牌的童装,购进时的单价是60元.根据市场调查,在一段时间内,销售单价是80元时,销售量是200件,而销售单价每降低1元,就可多售出20件.
(1)写出销售量y件与销售单价x元之间的函数关系式;
(2)写出销售该品牌童装获得的利润w元与销售单价x元之间的函数关系式;
(3)若童装厂规定该品牌童装销售单价不低于76元,且商场要完成不少于240件的销售任务,则商场销售该品牌童装获得的最大利润是多少?
2011-2012学年第一学期期末检测
九年级数学试题
第Ⅱ卷(共84分)
二、填空题(每题3分,共15分)
13. 14. 15.
16. 17.
三、解答题(共69分)
18、(8分)解方程:x(x-2)+x-2=0. (2)x2-3x+2=0
19、(9分)
20、(10分)
21、(10分)
22、(10分)
23、(10分)
24、(12分)
2011-2012学年第一学期期末检测
九年级数学试题
参考答案及评分说明
一、选择题(本题共12个小题,每小题3分,共36分)
题号 1 2 3 4 5 6 7 8 9 10 11 12
答案 B B A C A C D C D D B B
二、填空题(每小题填对得3分,满分15分)
13.± 14.y=(x-2) +1 15. 75°或15° 16.x≤2或x>0 17.π
三、解答题(满分69分)
18.(本题满分8分)
(1)x(x-2)+x-2=0,(因式分解法解)
(x-2)(x+1)=0,
x-2=0,或x+1=0,
x1=2,x2=-1; 4分
(2)x -3x+2=0
(x-2)(x-1)=0
x-2=0或x-1=0
x1=2或x2=1 4分
19.(本题满分8分)
如图所示,即为所求
设所在直线的解析式为
∵,
∴ 解得
∴ ················3分
⑵如图所示,即为所求 ···4分
由图可知, ·········5分
······················6分
=··············9分
20.(本题满分10分)
解
1、∵BD‖AE
∴∠E=∠BDC
∵DB平分∠ADC
∴∠BDC=∠BDA=1/2∠ADC
∵∠C=2∠E
∴∠C=2∠BDC=∠ADC
∴梯形ABCD为等腰梯形 ·····················5分
2、∵∠BDC=30° ∠C=2∠BDC
∴∠C=60°
∴∠CBD=90°
∴△CBD为直角三角形,∠BDC=30°
∴CD=2BC=2AD=2×5=10·····················10分
21.(本题满分10分)
解:(1)设每年市政府投资的增长率为x,
根据题意,得:2+2(1+x)+2(1+x)2=9.5,
整理,得:x2+3x-1.75=0, 解之,得:x=
∴x1=0.5 x2=-0.35(舍去),
答:每年市政府投资的增长率为50%;·····················5分
(2)到2012年底共建廉租房面积=9.5÷(万平方米).·····················10分
22.(本题满分10分)
解:1)由图可以看出:
∵反比例函数y=(4-2m)/x(x>0)图像在第四象限。
∴4-2m<0
∴m>2·····················4分
(2)把A(2,-4)代入
得:
-4=(4-2m)/2
∴m=6
∴反比例函数为:y=-8/x
把A(2,-4)代入y=kx+b,得:
2k+b=-4
∴b=-4-2k
∴一次函数的解析式为:y=kx-4-2k和反比例函数y=-8/x的交点为
-8/x=kx-4-2k
kx -(4+2k)+8=0
(kx-4)(x-2)=0
∴x1=2;x2=4/k
∴B点的坐标是(4/k,-2k)
∵一次函数y=kx+b与x轴的交点C坐标是:((4+2k/k),0)
BC/AB=1/3
BC/AC=1/4
∴ BC的纵坐标之差/AC的纵坐标之差=1:4
即 [0-(-2k)]:[(0-(-4)]=1:4
∴ k=1/2
∴ b=-4-2k=-4+1=-5
∴ 一次函数的解析式为:y=(1/2)x-5 ····················10分
23.(本题满分10分)
(1)∠AOD=60°
(2)第二问切线易证
24.(本题满分12分)
解:(1)根据题意得,y=200+(80-x)×20=-20x+1800,
∴销售量y件与销售单价x元之间的函数关系式为y=-20x+1800;·····················4分
(2)W=(x-60)y=(x-60)(-20x+1800)=-20x2+3000x-108000,
所以销售该品牌童装获得的利润w元与销售单价x元之间的函数关系式y=-20x2+3000x-108000;·····················8分
(3)根据题意得,-20x+1800≥240,x≥76,
∴76≤x≤78,
w=-20x2+3000x-108000,
对称轴为x=- 30002×(-20)=75,
a=-20<0,
∴当76≤x≤78时,W随x的增大而减小,
∴x=76时,W有最大值,最大值=(76-60)(-20×76+1800)=4480(元).
所以商场销售该品牌童装获得的最大利润是4480元.····················12分
说明:解答题各小题只给了一种解答及评分说明,其他解法只要步骤合理、解答正确,均应给出相应分数.
3题图
4题图
6题图
(-1,1)
(2,2)
x
y
O
7题图
10题图
17题图
O
C
B
A
x
y
2
-4
A
P
C
O
B
E
D
O
C
B
A
x
y
2
-4
A
P
C
O
B
E
D
A
B
C
O
B1
C1
A1
x
y
1
1
O
C
B
A
x
y
2
-4
同课章节目录
