高中数学人教A版选修2-1课件:3.1.1 空 间 向 量 及 其 加 减 运 算(共24张PPT)
文档属性
| 名称 | 高中数学人教A版选修2-1课件:3.1.1 空 间 向 量 及 其 加 减 运 算(共24张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 457.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-31 00:00:00 | ||
图片预览





文档简介
(共24张PPT)
第三章
空间向量与立体几何
3.1
空间向量及其运算
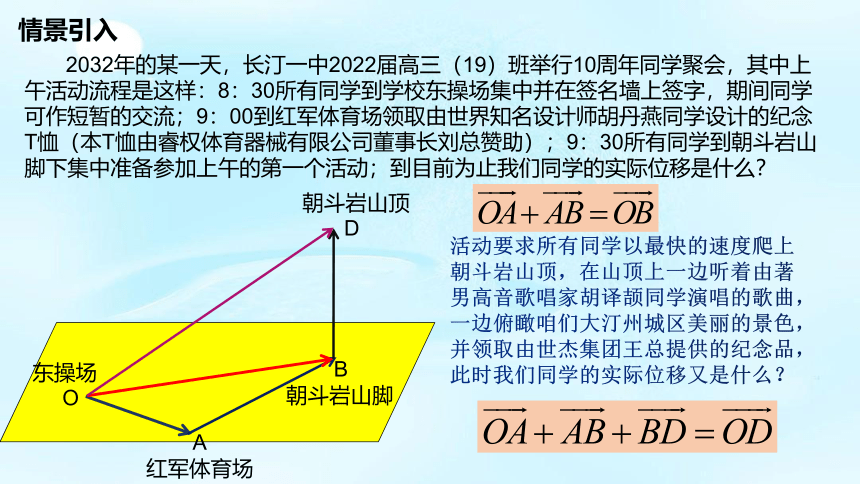
情景引入
2032年的某一天,长汀一中2022届高三(19)班举行10周年同学聚会,其中上午活动流程是这样:8:30所有同学到学校东操场集中并在签名墙上签字,期间同学可作短暂的交流;9:00到红军体育场领取由世界知名设计师胡丹燕同学设计的纪念T恤(本T恤由睿权体育器械有限公司董事长刘总赞助);9:30所有同学到朝斗岩山脚下集中准备参加上午的第一个活动;到目前为止我们同学的实际位移是什么?
东操场
O
A
红军体育场
B
朝斗岩山脚
朝斗岩山顶
D
活动要求所有同学以最快的速度爬上朝斗岩山顶,在山顶上一边听着由著男高音歌唱家胡译颉同学演唱的歌曲,一边俯瞰咱们大汀州城区美丽的景色,并领取由世杰集团王总提供的纪念品,此时我们同学的实际位移又是什么?
3.1.1
空
间
向
量
及
其
加
减
运
算
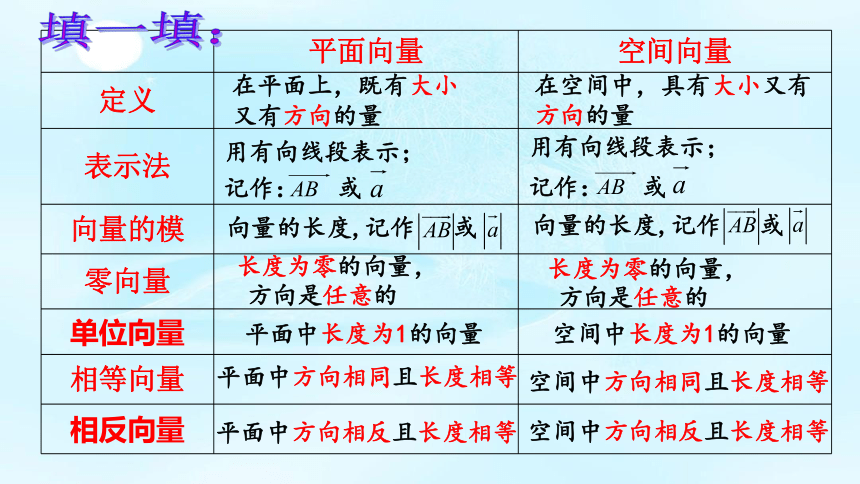
平面向量
空间向量
定义
表示法
向量的模
零向量
单位向量
相等向量
相反向量
在空间中,具有大小又有
方向的量
用有向线段表示;
记作:
或
长度为零的向量,
方向是任意的
空间中方向相反且长度相等
空间中方向相同且长度相等
空间中长度为1的向量
填一填:
在平面上,既有大小
又有方向的量
长度为零的向量,
方向是任意的
平面中长度为1的向量
平面中方向相反且长度相等
用有向线段表示;
记作:
或
平面中方向相同且长度相等
向量的长度,记作
或
向量的长度,记作
或
判断正误:
(1)两个空间向量相等,则它们的起点相同,终点也相同.
(4)空间中任意两个向量都可以平移到同一平面内,成为同一平面内的两个向量.
a
b
a
b
O
A
B
b
空间任意两个向量都可以平移到同一个平面内,成为同一平面内的两个向量。凡是涉及空间任意两个向量的问题,平面向量中有关结论仍适用于它们。
结
论
练一练:
(2)若空间向量
、
、
满足
,
,则
(3)两个空间向量模相等,则这两个向量相等.
对
错
错
对
平面向量
空间向量
加法运算
减法运算
三角形法则或平行四边形法则
三角形法则或平行
四边形法则
三角形法则
三角形法则
空间向量的运算法则
想一想:
O
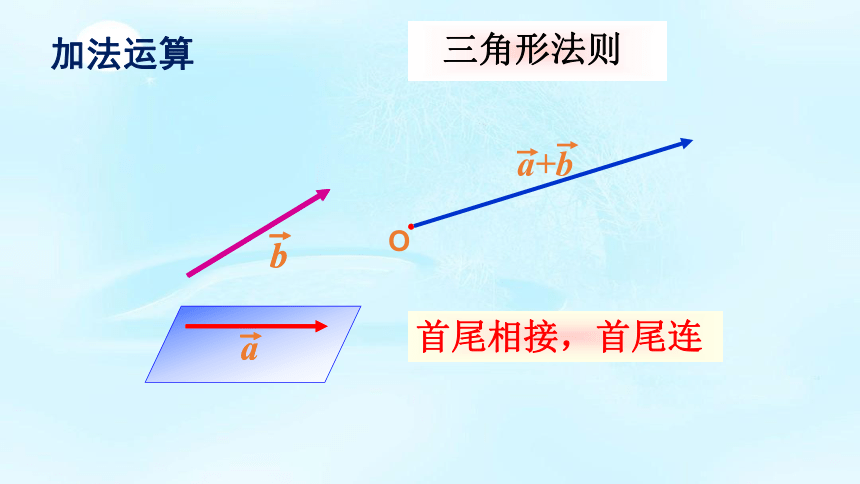
加法运算
a
a
b
b
a+b
平行四边形法则
共起点,对角线
O
首尾相接,首尾连
加法运算
三角形法则
b
a
a
b
a+b
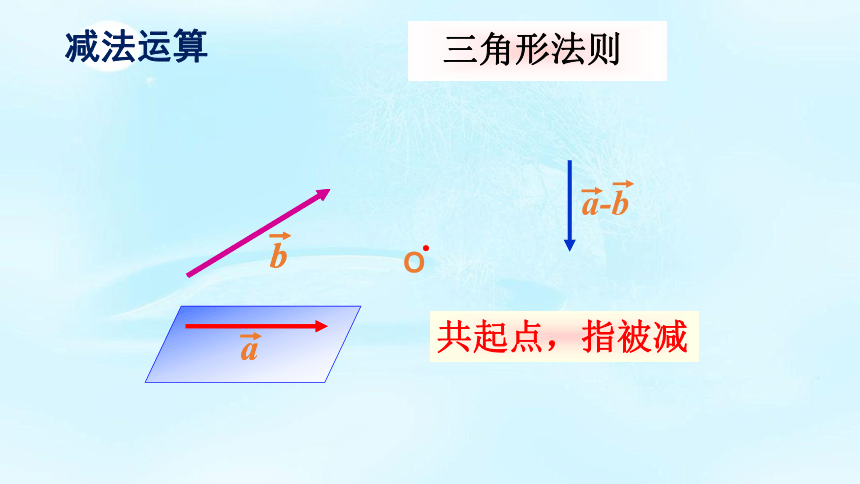
共起点,指被减
减法运算
b
a
a
b
a-b
O
三角形法则
(1)求三个、四个,乃至更多个空间向量的和,如何解决?
首尾相接的若干向量之和,等于由起始
向量的起点指向末尾向量的终点的向量;
想一想:
?
(2)若首尾相接的若干向量构成一个封闭图形,那么这些向量的和等于什么?
首尾相接的若干向量若构成一个封闭图形,则它们的和为零向量。
想一想:
平面向量
空间向量
加法交换律
加法结合律
空间向量的运算律
想一想:
a
+
b
+
c
a
+
b
b
+
c
a
+
b
+
c
议一议:
如何验证加法的结合律
加法结合律:
A
a
b
c
a
b
c
B
O
C
O
B
C
A
例1:已知平行六面体ABCD-A1B1C1D1,化简下列向量
表达式。
A
B
C
D
A1
B1
C1
D1
用一用:
例1:已知平行六面体ABCD-A1B1C1D1,化简下列向量
表达式。
A
B
C
D
A1
B1
C1
D1
用一用:
例1、已知平行六面体ABCD-A1B1C1D1,化简下列向量
表达式。
A1
D1
C1
B1
B
A
C
D
A1
D1
C1
B1
B
A
C
D
结
论
起点相同的三个不共面向量之和,等于以这三个向量为棱的平行六面体的以公共起点为始点的对角线所表示的向量。
三个不共面向量的和,等于以这三个向量为邻边的平行六面体的体对角线所表示的向量。
用一用:
1.已知平行六面体ABCD-A1B1C1D1,求满足下列各式的x的值。
A
B
C
D
A1
B1
C1
D1
练一练:
已知平行六面体ABCD-A1B1C1D1,
求满足下列各式的x的值。
A
B
C
D
A1
B1
C1
D1
已知平行六面体ABCD-A1B1C1D1,
求满足下列各式的x的值。
A
B
C
D
A1
B1
C1
D1
A
B
M
C
G
D
2.在空间四边形ABCD中,点M、G分别是BC、CD边的中点,化简
练一练:
A
B
M
C
G
D
A
2.在空间四边形ABCD中,点M、G分别是BC、CD边的中点,化简
练一练:
方法
空间向量
平面向量
类比
转化
基本概念
运算法则
运算律
结论1
结论2
课堂总结
1.课本P105
1
2.名校学案:
P46
4;
P84
1,3,4,5,6
3.预习
3.1.2空间向量的数乘运算
作业:
谢谢大家!
第三章
空间向量与立体几何
3.1
空间向量及其运算
情景引入
2032年的某一天,长汀一中2022届高三(19)班举行10周年同学聚会,其中上午活动流程是这样:8:30所有同学到学校东操场集中并在签名墙上签字,期间同学可作短暂的交流;9:00到红军体育场领取由世界知名设计师胡丹燕同学设计的纪念T恤(本T恤由睿权体育器械有限公司董事长刘总赞助);9:30所有同学到朝斗岩山脚下集中准备参加上午的第一个活动;到目前为止我们同学的实际位移是什么?
东操场
O
A
红军体育场
B
朝斗岩山脚
朝斗岩山顶
D
活动要求所有同学以最快的速度爬上朝斗岩山顶,在山顶上一边听着由著男高音歌唱家胡译颉同学演唱的歌曲,一边俯瞰咱们大汀州城区美丽的景色,并领取由世杰集团王总提供的纪念品,此时我们同学的实际位移又是什么?
3.1.1
空
间
向
量
及
其
加
减
运
算
平面向量
空间向量
定义
表示法
向量的模
零向量
单位向量
相等向量
相反向量
在空间中,具有大小又有
方向的量
用有向线段表示;
记作:
或
长度为零的向量,
方向是任意的
空间中方向相反且长度相等
空间中方向相同且长度相等
空间中长度为1的向量
填一填:
在平面上,既有大小
又有方向的量
长度为零的向量,
方向是任意的
平面中长度为1的向量
平面中方向相反且长度相等
用有向线段表示;
记作:
或
平面中方向相同且长度相等
向量的长度,记作
或
向量的长度,记作
或
判断正误:
(1)两个空间向量相等,则它们的起点相同,终点也相同.
(4)空间中任意两个向量都可以平移到同一平面内,成为同一平面内的两个向量.
a
b
a
b
O
A
B
b
空间任意两个向量都可以平移到同一个平面内,成为同一平面内的两个向量。凡是涉及空间任意两个向量的问题,平面向量中有关结论仍适用于它们。
结
论
练一练:
(2)若空间向量
、
、
满足
,
,则
(3)两个空间向量模相等,则这两个向量相等.
对
错
错
对
平面向量
空间向量
加法运算
减法运算
三角形法则或平行四边形法则
三角形法则或平行
四边形法则
三角形法则
三角形法则
空间向量的运算法则
想一想:
O
加法运算
a
a
b
b
a+b
平行四边形法则
共起点,对角线
O
首尾相接,首尾连
加法运算
三角形法则
b
a
a
b
a+b
共起点,指被减
减法运算
b
a
a
b
a-b
O
三角形法则
(1)求三个、四个,乃至更多个空间向量的和,如何解决?
首尾相接的若干向量之和,等于由起始
向量的起点指向末尾向量的终点的向量;
想一想:
?
(2)若首尾相接的若干向量构成一个封闭图形,那么这些向量的和等于什么?
首尾相接的若干向量若构成一个封闭图形,则它们的和为零向量。
想一想:
平面向量
空间向量
加法交换律
加法结合律
空间向量的运算律
想一想:
a
+
b
+
c
a
+
b
b
+
c
a
+
b
+
c
议一议:
如何验证加法的结合律
加法结合律:
A
a
b
c
a
b
c
B
O
C
O
B
C
A
例1:已知平行六面体ABCD-A1B1C1D1,化简下列向量
表达式。
A
B
C
D
A1
B1
C1
D1
用一用:
例1:已知平行六面体ABCD-A1B1C1D1,化简下列向量
表达式。
A
B
C
D
A1
B1
C1
D1
用一用:
例1、已知平行六面体ABCD-A1B1C1D1,化简下列向量
表达式。
A1
D1
C1
B1
B
A
C
D
A1
D1
C1
B1
B
A
C
D
结
论
起点相同的三个不共面向量之和,等于以这三个向量为棱的平行六面体的以公共起点为始点的对角线所表示的向量。
三个不共面向量的和,等于以这三个向量为邻边的平行六面体的体对角线所表示的向量。
用一用:
1.已知平行六面体ABCD-A1B1C1D1,求满足下列各式的x的值。
A
B
C
D
A1
B1
C1
D1
练一练:
已知平行六面体ABCD-A1B1C1D1,
求满足下列各式的x的值。
A
B
C
D
A1
B1
C1
D1
已知平行六面体ABCD-A1B1C1D1,
求满足下列各式的x的值。
A
B
C
D
A1
B1
C1
D1
A
B
M
C
G
D
2.在空间四边形ABCD中,点M、G分别是BC、CD边的中点,化简
练一练:
A
B
M
C
G
D
A
2.在空间四边形ABCD中,点M、G分别是BC、CD边的中点,化简
练一练:
方法
空间向量
平面向量
类比
转化
基本概念
运算法则
运算律
结论1
结论2
课堂总结
1.课本P105
1
2.名校学案:
P46
4;
P84
1,3,4,5,6
3.预习
3.1.2空间向量的数乘运算
作业:
谢谢大家!
