北师大版数学五年级上册5.4 分数与除法 课件(21张ppt)
文档属性
| 名称 | 北师大版数学五年级上册5.4 分数与除法 课件(21张ppt) |  | |
| 格式 | ppt | ||
| 文件大小 | 941.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-29 19:32:46 | ||
图片预览








文档简介
第4课时 分数与除法
五 分数的意义
一、情境引入
1.计算下面各题,你能把商分为哪几类?
36÷6= 4÷5= 80÷5=
3÷7= 5÷10= 4÷9=
6
0.8
16
0.42857…
0.5
0.444…
这些算式有什么共同特点?有什么不同?
一、情境引入
2.
(1)把一个西瓜平均分给5个人,每个人吃到这个西瓜的几分之几?
6÷5=1.2(盒)
(2)把6盒羽毛球分给5个班,每个班分得几盒?
1
5
一、情境引入
我们可以知道这些题目的算式都是除法算式,有一些能够整除,有一些需要用分数来表示,它们两者之间有什么关系呢?
二、学习新课
把1块蛋糕平均分给2个小朋友,每个人可以分到几块蛋糕?如果把7块蛋糕平均分给3个小朋友呢?
1块蛋糕平均分给2个小朋友,每个人分到几块蛋糕?
列式为:1÷2
把1块蛋糕平均分成2份,求每一份是多少?
答:1块蛋糕平均分给2个小朋友,每个人分到 块蛋糕。
用除法计算。
根据分数的意义。
1÷2=
1
2
二、学习新课
把1块蛋糕平均分给2个小朋友,每个人可以分到几块蛋糕?如果把7块蛋糕平均分给3个小朋友呢?
7块蛋糕平均分给3个小朋友,每个人分到几块蛋糕?
列式为:7÷3
把7块蛋糕平均分成3份,求每一份是多少?
答:7块蛋糕平均分给3个小朋友,每个人分到 块蛋糕。
7÷3=
7
3
二、学习新课
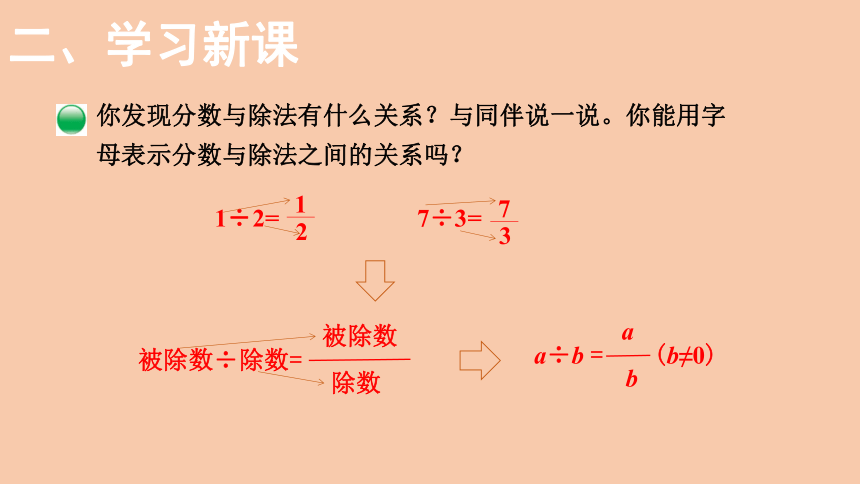
你发现分数与除法有什么关系?与同伴说一说。你能用字母表示分数与除法之间的关系吗?
1÷2=
1
2
7÷3=
7
3
被除数÷除数=
被除数
除数
a÷b = (b≠0)
a
b
二、学习新课
举例说一说,假分数和带分数如何进行互化?
利用分数与除法的关系,我们可以把假分数和带分数进行互化。
1
3
2
6+1
3
=
=
7
3
带分数化假分数:
= +
1
3
6
3
带分数化假分数时,用整数与分母的乘积再加上原来的分子作分子,分母不变。
二、学习新课
举例说一说,假分数和带分数如何进行互化?
利用分数与除法的关系,我们可以把假分数和带分数进行互化。
7
3
6+1
3
=
= +
1
3
6
3
=2+
1
3
1
3
2
=
假分数化带分数:
假分数化带分数时,用分子除以分母,用除得的商作为带分数的整数部分,用余数作分数部分的分子,分母不变。
二、学习新课
蓝纸条的长度是红纸条的几分之几?
红纸条
蓝纸条
二、学习新课
蓝纸条的长度是红纸条的几分之几?
笑笑认为:用除法直接计算 。
1÷3=
1
3
淘气认为:用蓝纸条去量红纸条,正好量了3次,蓝纸条的长度是红纸条的 。
二、学习新课
黄纸条的长度是红纸条的几分之几?
红纸条
黄纸条
二、学习新课
黄纸条的长度是红纸条的几分之几?
用除法直接计算, 。
4÷3=
4
3
黄纸条比红纸条长,结果大于1。
1÷3=
4÷3=
蓝纸条的长是红纸条的几分之几?
黄纸条的长是红纸条的几分之几?
求一个量是另一个量的几分之几,和求一个量是另一个量的几倍。使用的方法是一样的,都是用除法解决。
二、学习新课
三、巩固反馈
1.把1千克茶叶平均装在4个小罐里,每个小罐装多少千克?平均装在5
个小罐里呢?
(1)想一想,算一算,并与同伴交流。
(kg)
1÷4=
1
4
(kg)
1÷5=
1
5
答:把1千克茶叶平均装在4个小罐里,每个小罐装 千克;平均装在5个小罐,每小罐装 千克。
三、巩固反馈
1.把1千克茶叶平均装在4个小罐里,每个小罐装多少千克?平均装在5
个小罐里呢?
(2)请你再举一个例子,说明分数与除法的关系。
(kg)
1÷6=
1
6
答案不唯一,例如:平均装在6个小罐里呢?
答:每个小罐装 千克。
2.把10块巧克力平均分给3个人,每人分几块?平均分给4个人呢?5个
人呢?
三、巩固反馈
10÷3=
(块)
10
3
10÷4=
(块)
10
4
10÷5=
=2(块)
10
5
答:10块巧克力平均分给3个人,每人分到 块:平均分给4人,每人分到 块;平均分给5个人,每人分到2块。
3.把下列假分数化成整数或带分数,把带分数化成假分数。
三、巩固反馈
7
4
4+3
4
= =1
3
4
18
6
=18÷6=3
27
5
=27÷5=5
2
5
假分数化成带分数:
3.把下列假分数化成整数或带分数,把带分数化成假分数。
三、巩固反馈
带分数化成假分数:
11
8
1×8+3
8
= =
3
8
1
33
4
8×4+1
4
= =
1
4
8
13
5
2×5+3
5
= =
3
5
2
四、课堂小结
1.分数和除法之间存在的关系,被除数就相当于分数中的分子,除数相当于分数中的分母。
2.被除数÷除数=
被除数
除数
a÷b = (b≠0)
a
b
作业:
五、作业布置
五 分数的意义
一、情境引入
1.计算下面各题,你能把商分为哪几类?
36÷6= 4÷5= 80÷5=
3÷7= 5÷10= 4÷9=
6
0.8
16
0.42857…
0.5
0.444…
这些算式有什么共同特点?有什么不同?
一、情境引入
2.
(1)把一个西瓜平均分给5个人,每个人吃到这个西瓜的几分之几?
6÷5=1.2(盒)
(2)把6盒羽毛球分给5个班,每个班分得几盒?
1
5
一、情境引入
我们可以知道这些题目的算式都是除法算式,有一些能够整除,有一些需要用分数来表示,它们两者之间有什么关系呢?
二、学习新课
把1块蛋糕平均分给2个小朋友,每个人可以分到几块蛋糕?如果把7块蛋糕平均分给3个小朋友呢?
1块蛋糕平均分给2个小朋友,每个人分到几块蛋糕?
列式为:1÷2
把1块蛋糕平均分成2份,求每一份是多少?
答:1块蛋糕平均分给2个小朋友,每个人分到 块蛋糕。
用除法计算。
根据分数的意义。
1÷2=
1
2
二、学习新课
把1块蛋糕平均分给2个小朋友,每个人可以分到几块蛋糕?如果把7块蛋糕平均分给3个小朋友呢?
7块蛋糕平均分给3个小朋友,每个人分到几块蛋糕?
列式为:7÷3
把7块蛋糕平均分成3份,求每一份是多少?
答:7块蛋糕平均分给3个小朋友,每个人分到 块蛋糕。
7÷3=
7
3
二、学习新课
你发现分数与除法有什么关系?与同伴说一说。你能用字母表示分数与除法之间的关系吗?
1÷2=
1
2
7÷3=
7
3
被除数÷除数=
被除数
除数
a÷b = (b≠0)
a
b
二、学习新课
举例说一说,假分数和带分数如何进行互化?
利用分数与除法的关系,我们可以把假分数和带分数进行互化。
1
3
2
6+1
3
=
=
7
3
带分数化假分数:
= +
1
3
6
3
带分数化假分数时,用整数与分母的乘积再加上原来的分子作分子,分母不变。
二、学习新课
举例说一说,假分数和带分数如何进行互化?
利用分数与除法的关系,我们可以把假分数和带分数进行互化。
7
3
6+1
3
=
= +
1
3
6
3
=2+
1
3
1
3
2
=
假分数化带分数:
假分数化带分数时,用分子除以分母,用除得的商作为带分数的整数部分,用余数作分数部分的分子,分母不变。
二、学习新课
蓝纸条的长度是红纸条的几分之几?
红纸条
蓝纸条
二、学习新课
蓝纸条的长度是红纸条的几分之几?
笑笑认为:用除法直接计算 。
1÷3=
1
3
淘气认为:用蓝纸条去量红纸条,正好量了3次,蓝纸条的长度是红纸条的 。
二、学习新课
黄纸条的长度是红纸条的几分之几?
红纸条
黄纸条
二、学习新课
黄纸条的长度是红纸条的几分之几?
用除法直接计算, 。
4÷3=
4
3
黄纸条比红纸条长,结果大于1。
1÷3=
4÷3=
蓝纸条的长是红纸条的几分之几?
黄纸条的长是红纸条的几分之几?
求一个量是另一个量的几分之几,和求一个量是另一个量的几倍。使用的方法是一样的,都是用除法解决。
二、学习新课
三、巩固反馈
1.把1千克茶叶平均装在4个小罐里,每个小罐装多少千克?平均装在5
个小罐里呢?
(1)想一想,算一算,并与同伴交流。
(kg)
1÷4=
1
4
(kg)
1÷5=
1
5
答:把1千克茶叶平均装在4个小罐里,每个小罐装 千克;平均装在5个小罐,每小罐装 千克。
三、巩固反馈
1.把1千克茶叶平均装在4个小罐里,每个小罐装多少千克?平均装在5
个小罐里呢?
(2)请你再举一个例子,说明分数与除法的关系。
(kg)
1÷6=
1
6
答案不唯一,例如:平均装在6个小罐里呢?
答:每个小罐装 千克。
2.把10块巧克力平均分给3个人,每人分几块?平均分给4个人呢?5个
人呢?
三、巩固反馈
10÷3=
(块)
10
3
10÷4=
(块)
10
4
10÷5=
=2(块)
10
5
答:10块巧克力平均分给3个人,每人分到 块:平均分给4人,每人分到 块;平均分给5个人,每人分到2块。
3.把下列假分数化成整数或带分数,把带分数化成假分数。
三、巩固反馈
7
4
4+3
4
= =1
3
4
18
6
=18÷6=3
27
5
=27÷5=5
2
5
假分数化成带分数:
3.把下列假分数化成整数或带分数,把带分数化成假分数。
三、巩固反馈
带分数化成假分数:
11
8
1×8+3
8
= =
3
8
1
33
4
8×4+1
4
= =
1
4
8
13
5
2×5+3
5
= =
3
5
2
四、课堂小结
1.分数和除法之间存在的关系,被除数就相当于分数中的分子,除数相当于分数中的分母。
2.被除数÷除数=
被除数
除数
a÷b = (b≠0)
a
b
作业:
五、作业布置
同课章节目录
- 一 小数除法
- 1 精打细算
- 2 打扫卫生
- 3 谁打电话的时间长
- 4 人民币兑换
- 5 除得尽吗
- 6 调查“生活垃圾”
- 二 轴对称和平移
- 1 轴对称再认识(一)
- 2 轴对称再认识(二)
- 3 平移
- 4 欣赏与设计
- 三 倍数与因数
- 1 倍数与因数
- 2 探索活动:2、5的倍数的特征
- 3 探索活动:3的倍数的特征
- 4 找因数
- 5 找质数
- 四 多边形的面积
- 1 比较图形的面积
- 2 认识底和高
- 3 探索活动:平行四边形的面积
- 4 探索活动:三角形的面积
- 5 探索活动:梯形的面积
- 五 分数的意义
- 1 分数的再认识(一)
- 2 分数的再认识(二)
- 3 分饼
- 4 分数与除法
- 5 分数基本性质
- 6 找最大的公因数
- 7 约分
- 8 找最小的公倍数
- 9 分数的大小
- 六 组合图形的面积
- 1 组合图形的面积
- 2 探索活动:成长的脚印
- 3 公顷、平方千米
- 数学好玩
- 1 设计秋游方案
- 2 图形中的规律
- 3 尝试与猜测
- 七 可能性
- 1 谁先走
- 2 摸球游戏
