2020-2021学年鲁教五四新版六年级下册数学期末练习试题(word版含解析)
文档属性
| 名称 | 2020-2021学年鲁教五四新版六年级下册数学期末练习试题(word版含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 247.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-29 06:30:24 | ||
图片预览



文档简介
2020-2021学年鲁教五四新版六年级下册数学期末练习试题
一.选择题(共10小题,满分30分,每小题3分)
1.在下面四个图形中,∠1与∠2是对顶角的是( )
A.
B.
C.
D.
2.下面计算正确的是( )
A.x5+x5=x10
B.(x3)3=x6
C.(﹣3x2y3)2=9x4y6
D.(﹣bc)4÷(﹣bc)2=﹣b2c2
3.下面调查统计中,适合采用普查方式的是( )
A.华为手机的市场占有率
B.乘坐飞机的旅客是否携带了违禁物品
C.国家宝藏”专栏电视节目的收视率
D.“现代”汽车每百公里的耗油量
4.在灯塔O处观测到轮船A位于北偏西54°的方向,同时轮船B在南偏东15°的方向,那么∠AOB的大小为( )
A.69°
B.111°
C.141°
D.159°
5.下列多项式乘法中可以用平方差公式计算的是( )
A.(2x+y)(y﹣2x)
B.(x+2)(2+x)
C.(﹣a+b)(a﹣b)
D.(x﹣2)(x+1)
6.弹簧挂上物体后会伸长,测得一弹簧的长度y(cm)与所挂的物体的质量x(kg)间有下面的关系(弹簧的弹性范围x≤10kg):
x
0
2
4
6
8
10
y
10
10.5
11
11.5
12
12.5
下列说法不正确的是( )
A.x与y都是变量,且x是自变量,y是因变量
B.弹簧不挂重物时的长度为10cm
C.所挂物体质量为5kg时,弹簧长度增加了1.25cm
D.所挂物体质量为9kg时,弹簧长度增加到11.25cm
7.计算(﹣)2018×(1.5)2019的结果是( )
A.﹣
B.
C.
D.﹣
8.市某视力健康管理中心对全市初中生的视力情况进行了一次抽样调查,如图是利用调查所得数据绘制的频数直方图,则这组数据的组数与组距分别是( )
A.4和0.20
B.4和0.30
C.5和0.20
D.5和0.30
9.下列说法中错误的是( )
A.(3.14﹣π)0=1
B.若x2+=9,则x+=±3
C.a﹣n(a≠0)是an的倒数
D.若am=2,an=3,则am+n=6
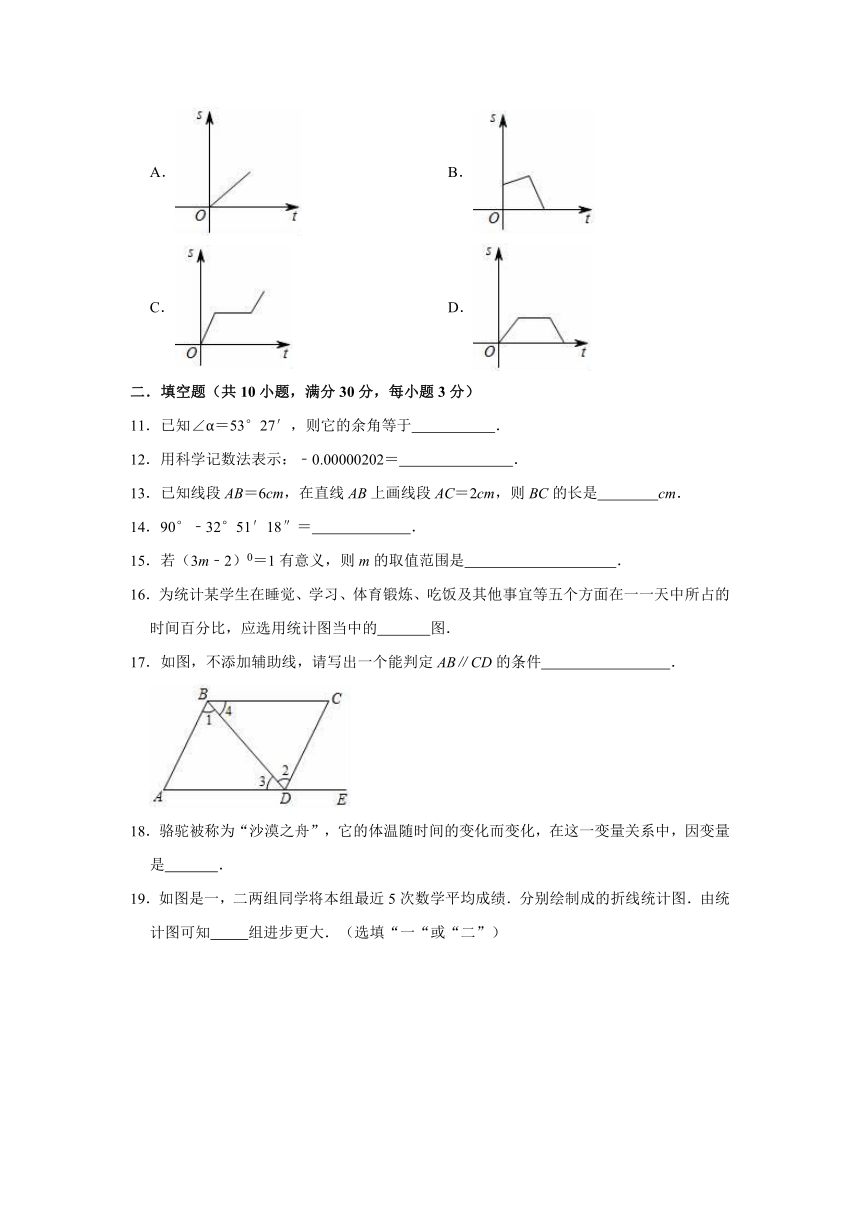
10.小新骑车去学校,骑了一会后车子出了故障,修了一会,然后继续骑车去学校.如果用横坐标表示时间t,纵坐标表示路程s,下列各图能较好地反映s与t之间函数关系的是( )
A.
B.
C.
D.
二.填空题(共10小题,满分30分,每小题3分)
11.已知∠α=53°27′,则它的余角等于
.
12.用科学记数法表示:﹣0.00000202=
.
13.已知线段AB=6cm,在直线AB上画线段AC=2cm,则BC的长是
cm.
14.90°﹣32°51′18″=
.
15.若(3m﹣2)0=1有意义,则m的取值范围是
.
16.为统计某学生在睡觉、学习、体育锻炼、吃饭及其他事宜等五个方面在一一天中所占的时间百分比,应选用统计图当中的
图.
17.如图,不添加辅助线,请写出一个能判定AB∥CD的条件
.
18.骆驼被称为“沙漠之舟”,它的体温随时间的变化而变化,在这一变量关系中,因变量是
.
19.如图是一,二两组同学将本组最近5次数学平均成绩.分别绘制成的折线统计图.由统计图可知
组进步更大.(选填“一“或“二”)
20.某剧院观众席的座位按下列方法设置:
排数(x)
1
2
3
4
…
座位数(y)
25
28
31
34
…
(1)写出座位数y与排数x(x≥1的正整数)之间的关系式
;
(2)第11排的座位数达到
个;
(3)按照上表所示的规律,某一排可能有75个座位吗?
.(填可能或不可能)
三.解答题(共9小题,满分60分)
21.计算
(1)(﹣x2y)3?(﹣3xy2)
(2)(xy+z)(﹣xy+z)
22.先化简,再求值:
(1)6x2y(﹣2xy+y3)÷xy2,其中x=2,y=﹣1;
(2)(x+2y)(x﹣2y)+(x﹣2y)2﹣(6x2y﹣2xy2)÷(2y),其中x=﹣2,y=.
23.如图,AB,CD为两条射线,AB∥CD,连接AC.
(1)尺规作图:在CD上找一点E,使得AE平分∠BAC,交CD于点E.(不写作法,保留作图痕迹).
(2)在题(1)所作的图形中,若∠C=120°,求∠CEA的度数.
24.如图,点A、O、E在同一直线上,∠AOB=50°,∠EOD=28°42',OD平分∠COE.
(1)∠AOB的余角是多少度?
(2)求∠COB的度数.
25.如图,AD∥BE,∠ACB=90°,∠CBE=40°,求∠CAD的度数.
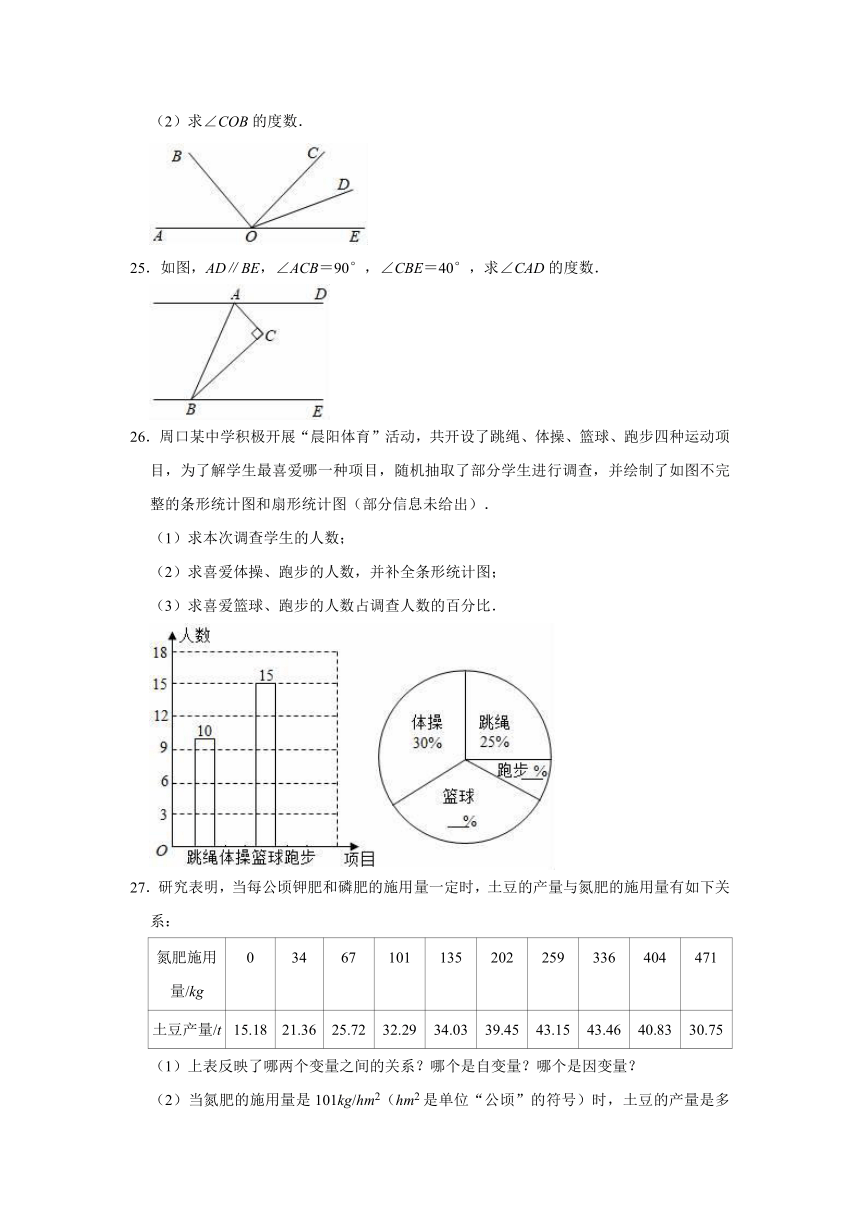
26.周口某中学积极开展“晨阳体育”活动,共开设了跳绳、体操、篮球、跑步四种运动项目,为了解学生最喜爱哪一种项目,随机抽取了部分学生进行调查,并绘制了如图不完整的条形统计图和扇形统计图(部分信息未给出).
(1)求本次调查学生的人数;
(2)求喜爱体操、跑步的人数,并补全条形统计图;
(3)求喜爱篮球、跑步的人数占调查人数的百分比.
27.研究表明,当每公顷钾肥和磷肥的施用量一定时,土豆的产量与氮肥的施用量有如下关系:
氮肥施用量/kg
0
34
67
101
135
202
259
336
404
471
土豆产量/t
15.18
21.36
25.72
32.29
34.03
39.45
43.15
43.46
40.83
30.75
(1)上表反映了哪两个变量之间的关系?哪个是自变量?哪个是因变量?
(2)当氮肥的施用量是101kg/hm2(hm2是单位“公顷”的符号)时,土豆的产量是多少?如果不施氮肥呢?
(3)根据表格中的数据,你认为氮肥的施用量是多少时比较适宜?说说你的理由.
(4)粗略说一说氮肥的施用量对土豆产量的影响.
28.若△ABC中∠A=60°,∠B的度数为x,∠C的度数为y,试写出y与x之间的函数关系式,并画出图象.
29.如图,∠1=∠2,∠3=∠D,∠4=∠5,设BC,AE的交点为G,求证:AE∥BF.请在括号内填推理的依据或数学式.
证明:∵∠1=∠2,
∴AB∥DF(内错角相等.两直线平行).
∴∠3=∠BCF(
).
∵∠3=∠D,
∴∠D=
.
∴
(
),
∴∠5=
(
).
∵∠4=∠5,
∴
.
∴AE∥BF.
参考答案与试题解析
一.选择题(共10小题,满分30分,每小题3分)
1.解:A、∠1与∠2不是对顶角;
B、∠1与∠2是对顶角;
C、∠1与∠2不是对顶角;
D、∠1与∠2不是对顶角;
故选:B.
2.解:A.x5+x5=2x5,所以A选项错误;
B.(x3)3=x9,所以B选项错误;
C.(﹣3x2y3)2=9x4y6,所以C选项正确;
D.(﹣bc)4÷(﹣bc)2=b2c2,所以D选项错误.
故选:C.
3.解:A、对华为手机的市场占有率的调查范围广,适合抽样调查,故此选项不符合题意;
B、对乘坐飞机的旅客是否携带了违禁物品的调查情况适合普查,故此选项符合题意;
C、对国家宝藏”专栏电视节目的收视率的调查范围广,适合抽样调查,故此选项不符合题意;
D、对“现代”汽车每百公里的耗油量的调查范围广适合抽样调查,故此选项不符合题意;
故选:B.
4.解:由题意得:∠1=54°,∠2=15°,
∠3=90°﹣54°=36°,
∠AOB=36°+90°+15°=141°,
故选:C.
5.解:A、(2x+y)(y﹣2x),能用平方差公式进行计算,故本选项符合题意;
B、(x+2)(2+x),不能用平方差公式进行计算,故本选项不符合题意;
C、(﹣a+b)(a﹣b),不能用平方差公式进行计算,故本选项不符合题意;
D、(x﹣2)(x+1)不能用平方差公式进行计算,故本选项不符合题意;
故选:A.
6.解:A.x与y都是变量,且x是自变量,y是因变量,故A不符合题意;
B.弹簧不挂重物时的长度为10cm,故B不符合题意;
C.所挂物体质量为5kg时,弹簧长度增加了0.25cm,故C不符合题意;
D.所挂物体质量为9kg时,弹簧长度增加到12.25cm,故D符合题意.
故选:D.
7.解:(﹣)2018×(1.5)2019
=()2018×(1.5)2018×1.5
=
=.
故选:B.
8.解:由频数分布直方图可知,
组数是5,组距是4.25﹣3.95=0.30,
故选:D.
9.解:任何不为0的0次幂均等于1,因此选项A正确;
当x2+=9时,x+=,因此选项B不正确;
因为a﹣n=,因此选项C正确;
因为am+n=am?an=3×2=6,因此选项D正确;
故选:B.
10.解:小新开始骑车去学校,所以S随t增大而增大,
车子出故障后S不随时间变化而变化,
最后恢复运动,S继续随时间增大而增大,
观察图象,C满足题意.
故选:C.
二.填空题(共10小题,满分30分,每小题3分)
11.解:根据定义∠α的余角度数是90°﹣53°27′=36°33′.
故答案为:36°33′.
12.解:﹣0.00000202=﹣2.02×10﹣6.
故答案为:﹣2.02×10﹣6.
13.解:线段AB=6cm,AC=2cm,
若A、B在C的同侧,则BC的长是6﹣2=4cm;
若A、B在C的两侧,则BC的是6+2=8cm;BC的长是8cm或4cm.
故答案为4或8.
14.解:90°﹣32°51′18″=89°59′60″﹣32°51′18″.
故答案为:57°8′42″.
15.解:∵(3m﹣2)0=1有意义,
∴3m﹣2≠0,
解得:m≠,
∴若(3m﹣2)0=1有意义,则m的取值范围:m≠.
故答案为:m≠.
16.解:为统计某学生在睡觉、学习、体育锻炼、吃饭及其他事宜等五个方面在一天中所占的时间百分比,
因此反映各个部分占整体的百分比,故选:扇形统计图,即扇形图,
故答案为:扇形.
17.解:添加∠1=∠2,
∵∠1=∠2,
∴AB∥CD(内错角相等,两直线平行),
故答案为:∠1=∠2(答案不唯一).
18.解:∵骆驼的体温随时间的变化而变化,
∴自变量是时间,因变量是体温,
故答案为:体温
19.解:一组的成绩变化从70到90,二组的成绩变化是从70到85,所以一组进步更大.
故答案为:一.
20.解:(1)由表格可知,排数每增加1,座位数增加3,
∴关系为y=3x+22;
故答案为y=3x+22;
(2)当x=11时,y=3×11+22=55,
故答案为55;
(3)当y=75时,3x+22=75,
解得x=不是整数解,
∴不可能;
故答案为不可能.
三.解答题(共9小题,满分60分)
21.解:(1)原式=(﹣x6y3)?(﹣3xy2)
=(﹣)×(﹣3)?x2×3+1y3+2
=x7y5;
(2)原式=z2﹣x2y2.
22.解:(1)6x2y(﹣2xy+y3)÷xy2,
=(﹣12x3y2+6x2y4)÷xy2
=﹣12x2+6xy2,
当x=2,y=﹣1时,
原式=﹣12×22+6×2×(﹣1)2
=﹣36;
(2)(x+2y)(x﹣2y)+(x﹣2y)2﹣(6x2y﹣2xy2)÷(2y)
=x2﹣4y2+x2﹣4xy+4y2﹣3x2+xy
=﹣x2﹣3xy,
当x=﹣2,y=时,
原式=﹣(﹣2)2﹣3×(﹣2)×
=﹣4+3
=﹣1.
23.解:(1)如图,射线AE即为所求.
(2)∵AB∥CD,
∴∠C+∠CAB=180°,
∵∠C=120°,
∴∠CAB=60°,
∵AE平分∠CAB,
∴∠BAE=∠CAB=30°,
∴∠AEC=∠BAE=30°.
24.解:(1)∵∠AOB=50°,
∴∠AOB的余角为:90°﹣50°=40°;
(2)∵OD平分∠COE,
∴∠EOC=2∠EOD=2×28°42'=57°24',
又∵∠AOE=∠AOB+∠COB+∠EOC,
而且点A、O、E在同一直线上,
∴∠AOE=180°,
∴∠COB=∠AOE﹣∠AOB﹣∠EOC=180°﹣57°24'=72°36'.
25.解:过点C作CF∥AD,
∵AD∥BE,
∴CF∥BE,
∴∠CAD=∠ACF,∠CBE=∠FCB,
∴∠ACB=∠CAD+∠CBE,
∴∠CAD=∠ACB﹣∠CBE=90°﹣40°=50°.
26.解:(1)本次调查的总人数是:10÷25%=40(人).
(2)喜欢体操的人数是:40×30%=12(人),
喜欢跑步的人数是40﹣10﹣12﹣15=3(人),
补全的条形统计图如图所示;
(3)喜爱篮球的人所占的百分比是:×100%=37.5%,
喜爱跑步的人所占的百分比是:×100%=7.5%.
27.解:(1)上表反映了土豆的产量与氮肥的施用量的关系;
(2)当氮肥的施用量是101千克/公顷时,土豆的产量是:32.29吨/公顷,
如果不施氮肥,土豆的产量是:15.18吨/公顷;
(3)当氮肥的施用量是336千克/公顷时,氮肥的施用量是比较适宜的,因为此时土豆产量最高,施肥太多或太少都会使土豆产量减产;
(4)当氮肥的施用量低于336千克/公顷时,土豆产量随氮肥的施用量的增加而增产,当氮肥的施用量高于336千克/公顷时,土豆产量随氮肥的施用量的增加而减产.
28.解:∵△ABC中∠A=60°,∠B的度数为x,∠C的度数为y,
∴∠A+x+y=180°,
∴y=120﹣x(0<x<120),图象如下:
29.证明:∵∠1=∠2,
∴AB∥DF(内错角相等.两直线平行).
∴∠3=∠BCF(
两直线平行,内错角相等).
∵∠3=∠D,
∴∠D=∠BCF.
∴AD∥BC,
∴∠5=∠CGE
(两直线平行,同位角相等
).
∵∠4=∠5,
∴∠4=∠CGE.
∴AE∥BF.
故答案为:两直线平行,内错角相等;∠BCF;AD∥BC;同位角相等,两直线平行;∠CGE;两直线平行,同位角相等;∠4=∠CGE.
一.选择题(共10小题,满分30分,每小题3分)
1.在下面四个图形中,∠1与∠2是对顶角的是( )
A.
B.
C.
D.
2.下面计算正确的是( )
A.x5+x5=x10
B.(x3)3=x6
C.(﹣3x2y3)2=9x4y6
D.(﹣bc)4÷(﹣bc)2=﹣b2c2
3.下面调查统计中,适合采用普查方式的是( )
A.华为手机的市场占有率
B.乘坐飞机的旅客是否携带了违禁物品
C.国家宝藏”专栏电视节目的收视率
D.“现代”汽车每百公里的耗油量
4.在灯塔O处观测到轮船A位于北偏西54°的方向,同时轮船B在南偏东15°的方向,那么∠AOB的大小为( )
A.69°
B.111°
C.141°
D.159°
5.下列多项式乘法中可以用平方差公式计算的是( )
A.(2x+y)(y﹣2x)
B.(x+2)(2+x)
C.(﹣a+b)(a﹣b)
D.(x﹣2)(x+1)
6.弹簧挂上物体后会伸长,测得一弹簧的长度y(cm)与所挂的物体的质量x(kg)间有下面的关系(弹簧的弹性范围x≤10kg):
x
0
2
4
6
8
10
y
10
10.5
11
11.5
12
12.5
下列说法不正确的是( )
A.x与y都是变量,且x是自变量,y是因变量
B.弹簧不挂重物时的长度为10cm
C.所挂物体质量为5kg时,弹簧长度增加了1.25cm
D.所挂物体质量为9kg时,弹簧长度增加到11.25cm
7.计算(﹣)2018×(1.5)2019的结果是( )
A.﹣
B.
C.
D.﹣
8.市某视力健康管理中心对全市初中生的视力情况进行了一次抽样调查,如图是利用调查所得数据绘制的频数直方图,则这组数据的组数与组距分别是( )
A.4和0.20
B.4和0.30
C.5和0.20
D.5和0.30
9.下列说法中错误的是( )
A.(3.14﹣π)0=1
B.若x2+=9,则x+=±3
C.a﹣n(a≠0)是an的倒数
D.若am=2,an=3,则am+n=6
10.小新骑车去学校,骑了一会后车子出了故障,修了一会,然后继续骑车去学校.如果用横坐标表示时间t,纵坐标表示路程s,下列各图能较好地反映s与t之间函数关系的是( )
A.
B.
C.
D.
二.填空题(共10小题,满分30分,每小题3分)
11.已知∠α=53°27′,则它的余角等于
.
12.用科学记数法表示:﹣0.00000202=
.
13.已知线段AB=6cm,在直线AB上画线段AC=2cm,则BC的长是
cm.
14.90°﹣32°51′18″=
.
15.若(3m﹣2)0=1有意义,则m的取值范围是
.
16.为统计某学生在睡觉、学习、体育锻炼、吃饭及其他事宜等五个方面在一一天中所占的时间百分比,应选用统计图当中的
图.
17.如图,不添加辅助线,请写出一个能判定AB∥CD的条件
.
18.骆驼被称为“沙漠之舟”,它的体温随时间的变化而变化,在这一变量关系中,因变量是
.
19.如图是一,二两组同学将本组最近5次数学平均成绩.分别绘制成的折线统计图.由统计图可知
组进步更大.(选填“一“或“二”)
20.某剧院观众席的座位按下列方法设置:
排数(x)
1
2
3
4
…
座位数(y)
25
28
31
34
…
(1)写出座位数y与排数x(x≥1的正整数)之间的关系式
;
(2)第11排的座位数达到
个;
(3)按照上表所示的规律,某一排可能有75个座位吗?
.(填可能或不可能)
三.解答题(共9小题,满分60分)
21.计算
(1)(﹣x2y)3?(﹣3xy2)
(2)(xy+z)(﹣xy+z)
22.先化简,再求值:
(1)6x2y(﹣2xy+y3)÷xy2,其中x=2,y=﹣1;
(2)(x+2y)(x﹣2y)+(x﹣2y)2﹣(6x2y﹣2xy2)÷(2y),其中x=﹣2,y=.
23.如图,AB,CD为两条射线,AB∥CD,连接AC.
(1)尺规作图:在CD上找一点E,使得AE平分∠BAC,交CD于点E.(不写作法,保留作图痕迹).
(2)在题(1)所作的图形中,若∠C=120°,求∠CEA的度数.
24.如图,点A、O、E在同一直线上,∠AOB=50°,∠EOD=28°42',OD平分∠COE.
(1)∠AOB的余角是多少度?
(2)求∠COB的度数.
25.如图,AD∥BE,∠ACB=90°,∠CBE=40°,求∠CAD的度数.
26.周口某中学积极开展“晨阳体育”活动,共开设了跳绳、体操、篮球、跑步四种运动项目,为了解学生最喜爱哪一种项目,随机抽取了部分学生进行调查,并绘制了如图不完整的条形统计图和扇形统计图(部分信息未给出).
(1)求本次调查学生的人数;
(2)求喜爱体操、跑步的人数,并补全条形统计图;
(3)求喜爱篮球、跑步的人数占调查人数的百分比.
27.研究表明,当每公顷钾肥和磷肥的施用量一定时,土豆的产量与氮肥的施用量有如下关系:
氮肥施用量/kg
0
34
67
101
135
202
259
336
404
471
土豆产量/t
15.18
21.36
25.72
32.29
34.03
39.45
43.15
43.46
40.83
30.75
(1)上表反映了哪两个变量之间的关系?哪个是自变量?哪个是因变量?
(2)当氮肥的施用量是101kg/hm2(hm2是单位“公顷”的符号)时,土豆的产量是多少?如果不施氮肥呢?
(3)根据表格中的数据,你认为氮肥的施用量是多少时比较适宜?说说你的理由.
(4)粗略说一说氮肥的施用量对土豆产量的影响.
28.若△ABC中∠A=60°,∠B的度数为x,∠C的度数为y,试写出y与x之间的函数关系式,并画出图象.
29.如图,∠1=∠2,∠3=∠D,∠4=∠5,设BC,AE的交点为G,求证:AE∥BF.请在括号内填推理的依据或数学式.
证明:∵∠1=∠2,
∴AB∥DF(内错角相等.两直线平行).
∴∠3=∠BCF(
).
∵∠3=∠D,
∴∠D=
.
∴
(
),
∴∠5=
(
).
∵∠4=∠5,
∴
.
∴AE∥BF.
参考答案与试题解析
一.选择题(共10小题,满分30分,每小题3分)
1.解:A、∠1与∠2不是对顶角;
B、∠1与∠2是对顶角;
C、∠1与∠2不是对顶角;
D、∠1与∠2不是对顶角;
故选:B.
2.解:A.x5+x5=2x5,所以A选项错误;
B.(x3)3=x9,所以B选项错误;
C.(﹣3x2y3)2=9x4y6,所以C选项正确;
D.(﹣bc)4÷(﹣bc)2=b2c2,所以D选项错误.
故选:C.
3.解:A、对华为手机的市场占有率的调查范围广,适合抽样调查,故此选项不符合题意;
B、对乘坐飞机的旅客是否携带了违禁物品的调查情况适合普查,故此选项符合题意;
C、对国家宝藏”专栏电视节目的收视率的调查范围广,适合抽样调查,故此选项不符合题意;
D、对“现代”汽车每百公里的耗油量的调查范围广适合抽样调查,故此选项不符合题意;
故选:B.
4.解:由题意得:∠1=54°,∠2=15°,
∠3=90°﹣54°=36°,
∠AOB=36°+90°+15°=141°,
故选:C.
5.解:A、(2x+y)(y﹣2x),能用平方差公式进行计算,故本选项符合题意;
B、(x+2)(2+x),不能用平方差公式进行计算,故本选项不符合题意;
C、(﹣a+b)(a﹣b),不能用平方差公式进行计算,故本选项不符合题意;
D、(x﹣2)(x+1)不能用平方差公式进行计算,故本选项不符合题意;
故选:A.
6.解:A.x与y都是变量,且x是自变量,y是因变量,故A不符合题意;
B.弹簧不挂重物时的长度为10cm,故B不符合题意;
C.所挂物体质量为5kg时,弹簧长度增加了0.25cm,故C不符合题意;
D.所挂物体质量为9kg时,弹簧长度增加到12.25cm,故D符合题意.
故选:D.
7.解:(﹣)2018×(1.5)2019
=()2018×(1.5)2018×1.5
=
=.
故选:B.
8.解:由频数分布直方图可知,
组数是5,组距是4.25﹣3.95=0.30,
故选:D.
9.解:任何不为0的0次幂均等于1,因此选项A正确;
当x2+=9时,x+=,因此选项B不正确;
因为a﹣n=,因此选项C正确;
因为am+n=am?an=3×2=6,因此选项D正确;
故选:B.
10.解:小新开始骑车去学校,所以S随t增大而增大,
车子出故障后S不随时间变化而变化,
最后恢复运动,S继续随时间增大而增大,
观察图象,C满足题意.
故选:C.
二.填空题(共10小题,满分30分,每小题3分)
11.解:根据定义∠α的余角度数是90°﹣53°27′=36°33′.
故答案为:36°33′.
12.解:﹣0.00000202=﹣2.02×10﹣6.
故答案为:﹣2.02×10﹣6.
13.解:线段AB=6cm,AC=2cm,
若A、B在C的同侧,则BC的长是6﹣2=4cm;
若A、B在C的两侧,则BC的是6+2=8cm;BC的长是8cm或4cm.
故答案为4或8.
14.解:90°﹣32°51′18″=89°59′60″﹣32°51′18″.
故答案为:57°8′42″.
15.解:∵(3m﹣2)0=1有意义,
∴3m﹣2≠0,
解得:m≠,
∴若(3m﹣2)0=1有意义,则m的取值范围:m≠.
故答案为:m≠.
16.解:为统计某学生在睡觉、学习、体育锻炼、吃饭及其他事宜等五个方面在一天中所占的时间百分比,
因此反映各个部分占整体的百分比,故选:扇形统计图,即扇形图,
故答案为:扇形.
17.解:添加∠1=∠2,
∵∠1=∠2,
∴AB∥CD(内错角相等,两直线平行),
故答案为:∠1=∠2(答案不唯一).
18.解:∵骆驼的体温随时间的变化而变化,
∴自变量是时间,因变量是体温,
故答案为:体温
19.解:一组的成绩变化从70到90,二组的成绩变化是从70到85,所以一组进步更大.
故答案为:一.
20.解:(1)由表格可知,排数每增加1,座位数增加3,
∴关系为y=3x+22;
故答案为y=3x+22;
(2)当x=11时,y=3×11+22=55,
故答案为55;
(3)当y=75时,3x+22=75,
解得x=不是整数解,
∴不可能;
故答案为不可能.
三.解答题(共9小题,满分60分)
21.解:(1)原式=(﹣x6y3)?(﹣3xy2)
=(﹣)×(﹣3)?x2×3+1y3+2
=x7y5;
(2)原式=z2﹣x2y2.
22.解:(1)6x2y(﹣2xy+y3)÷xy2,
=(﹣12x3y2+6x2y4)÷xy2
=﹣12x2+6xy2,
当x=2,y=﹣1时,
原式=﹣12×22+6×2×(﹣1)2
=﹣36;
(2)(x+2y)(x﹣2y)+(x﹣2y)2﹣(6x2y﹣2xy2)÷(2y)
=x2﹣4y2+x2﹣4xy+4y2﹣3x2+xy
=﹣x2﹣3xy,
当x=﹣2,y=时,
原式=﹣(﹣2)2﹣3×(﹣2)×
=﹣4+3
=﹣1.
23.解:(1)如图,射线AE即为所求.
(2)∵AB∥CD,
∴∠C+∠CAB=180°,
∵∠C=120°,
∴∠CAB=60°,
∵AE平分∠CAB,
∴∠BAE=∠CAB=30°,
∴∠AEC=∠BAE=30°.
24.解:(1)∵∠AOB=50°,
∴∠AOB的余角为:90°﹣50°=40°;
(2)∵OD平分∠COE,
∴∠EOC=2∠EOD=2×28°42'=57°24',
又∵∠AOE=∠AOB+∠COB+∠EOC,
而且点A、O、E在同一直线上,
∴∠AOE=180°,
∴∠COB=∠AOE﹣∠AOB﹣∠EOC=180°﹣57°24'=72°36'.
25.解:过点C作CF∥AD,
∵AD∥BE,
∴CF∥BE,
∴∠CAD=∠ACF,∠CBE=∠FCB,
∴∠ACB=∠CAD+∠CBE,
∴∠CAD=∠ACB﹣∠CBE=90°﹣40°=50°.
26.解:(1)本次调查的总人数是:10÷25%=40(人).
(2)喜欢体操的人数是:40×30%=12(人),
喜欢跑步的人数是40﹣10﹣12﹣15=3(人),
补全的条形统计图如图所示;
(3)喜爱篮球的人所占的百分比是:×100%=37.5%,
喜爱跑步的人所占的百分比是:×100%=7.5%.
27.解:(1)上表反映了土豆的产量与氮肥的施用量的关系;
(2)当氮肥的施用量是101千克/公顷时,土豆的产量是:32.29吨/公顷,
如果不施氮肥,土豆的产量是:15.18吨/公顷;
(3)当氮肥的施用量是336千克/公顷时,氮肥的施用量是比较适宜的,因为此时土豆产量最高,施肥太多或太少都会使土豆产量减产;
(4)当氮肥的施用量低于336千克/公顷时,土豆产量随氮肥的施用量的增加而增产,当氮肥的施用量高于336千克/公顷时,土豆产量随氮肥的施用量的增加而减产.
28.解:∵△ABC中∠A=60°,∠B的度数为x,∠C的度数为y,
∴∠A+x+y=180°,
∴y=120﹣x(0<x<120),图象如下:
29.证明:∵∠1=∠2,
∴AB∥DF(内错角相等.两直线平行).
∴∠3=∠BCF(
两直线平行,内错角相等).
∵∠3=∠D,
∴∠D=∠BCF.
∴AD∥BC,
∴∠5=∠CGE
(两直线平行,同位角相等
).
∵∠4=∠5,
∴∠4=∠CGE.
∴AE∥BF.
故答案为:两直线平行,内错角相等;∠BCF;AD∥BC;同位角相等,两直线平行;∠CGE;两直线平行,同位角相等;∠4=∠CGE.
同课章节目录
