2020-2021学年鲁教五四新版七年级下册数学期末练习试题(word版含解析)
文档属性
| 名称 | 2020-2021学年鲁教五四新版七年级下册数学期末练习试题(word版含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 326.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-29 06:34:59 | ||
图片预览



文档简介
2020-2021学年鲁教五四新版七年级下册数学期末练习试题
一.选择题(共12小题,满分48分,每小题4分)
1.商场举行摸奖促销活动,对于“抽到一等奖的概率为0.1”.下列说法正确的是( )
A.抽10次奖必有一次抽到一等奖
B.抽一次不可能抽到一等奖
C.抽10次也可能没有抽到一等奖
D.抽了9次如果没有抽到一等奖,那么再抽一次肯定抽到一等奖
2.下列方程组中不是二元一次方程组的是( )
A.
B.
C.
D.
3.如图,下列条件:①∠1=∠2,②∠3+∠4=180°,③∠5+∠6=180°,④∠2=∠3,⑤∠7=∠2+∠3,⑥∠7+∠4﹣∠1=180°中能判断直线a∥b的有( )
A.3个
B.4个
C.5个
D.6个
4.一个不透明的袋子中只装有5个红球,从中随机摸出一个球是黑球( )
A.属于随机事件
B.可能性大小为
C.属于不可能事件
D.是必然事件
5.等腰三角形两边的长分别为3cm和5cm,则这个三角形的周长是( )
A.11cm
B.13cm
C.11cm或13cm
D.不确定
6.如图,AB∥EF,∠C=90°,则α、β、γ的关系为( )
A.β=α+γ
B.α+β﹣γ=90°
C.α+β+γ=180°
D.β+γ﹣α=90°
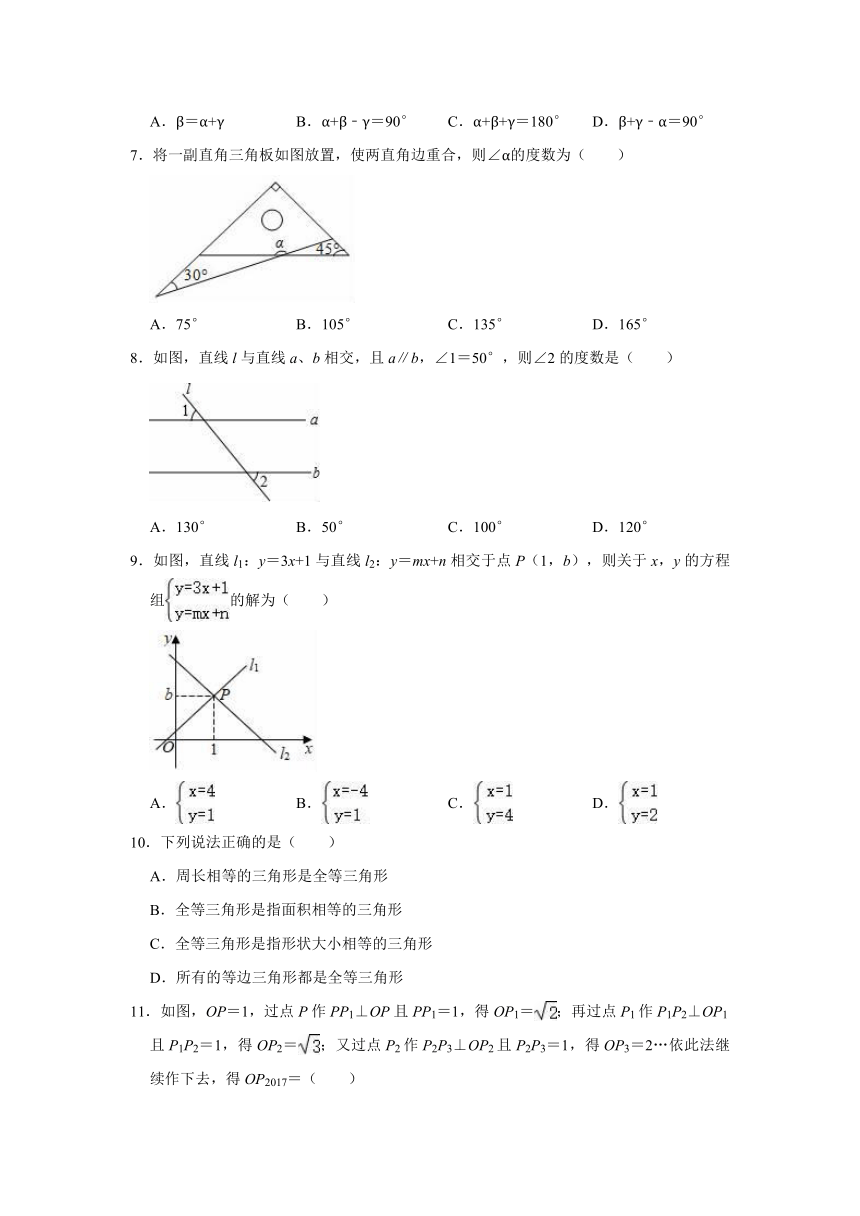
7.将一副直角三角板如图放置,使两直角边重合,则∠α的度数为( )
A.75°
B.105°
C.135°
D.165°
8.如图,直线l与直线a、b相交,且a∥b,∠1=50°,则∠2的度数是( )
A.130°
B.50°
C.100°
D.120°
9.如图,直线l1:y=3x+1与直线l2:y=mx+n相交于点P(1,b),则关于x,y的方程组的解为( )
A.
B.
C.
D.
10.下列说法正确的是( )
A.周长相等的三角形是全等三角形
B.全等三角形是指面积相等的三角形
C.全等三角形是指形状大小相等的三角形
D.所有的等边三角形都是全等三角形
11.如图,OP=1,过点P作PP1⊥OP且PP1=1,得OP1=;再过点P1作P1P2⊥OP1且P1P2=1,得OP2=;又过点P2作P2P3⊥OP2且P2P3=1,得OP3=2…依此法继续作下去,得OP2017=( )
A.
B.
C.
D.
12.如图,在Rt△ABC中,∠C=90°,BE平分∠ABC,ED垂直平分AB于D,若AC=9,则AE的值是( )
A.
B.
C.6
D.4
二.填空题(共6小题,满分24分,每小题4分)
13.若方程组的解也是二元一次方程x﹣y=1的一个解,则a=
.
14.有两双完全相同的鞋,从中任取两只,恰好成为一双的概率为
.
15.如图,黄芳不小心把一块三角形的玻璃打成三块碎片,现要带其中一块去配出与原来完全一样的玻璃,正确的办法是带来第
块去配,其依据是根据定理
(可以用字母简写)
16.已知:如图,∠1=∠2=∠3=54°,则∠4的度数是
.
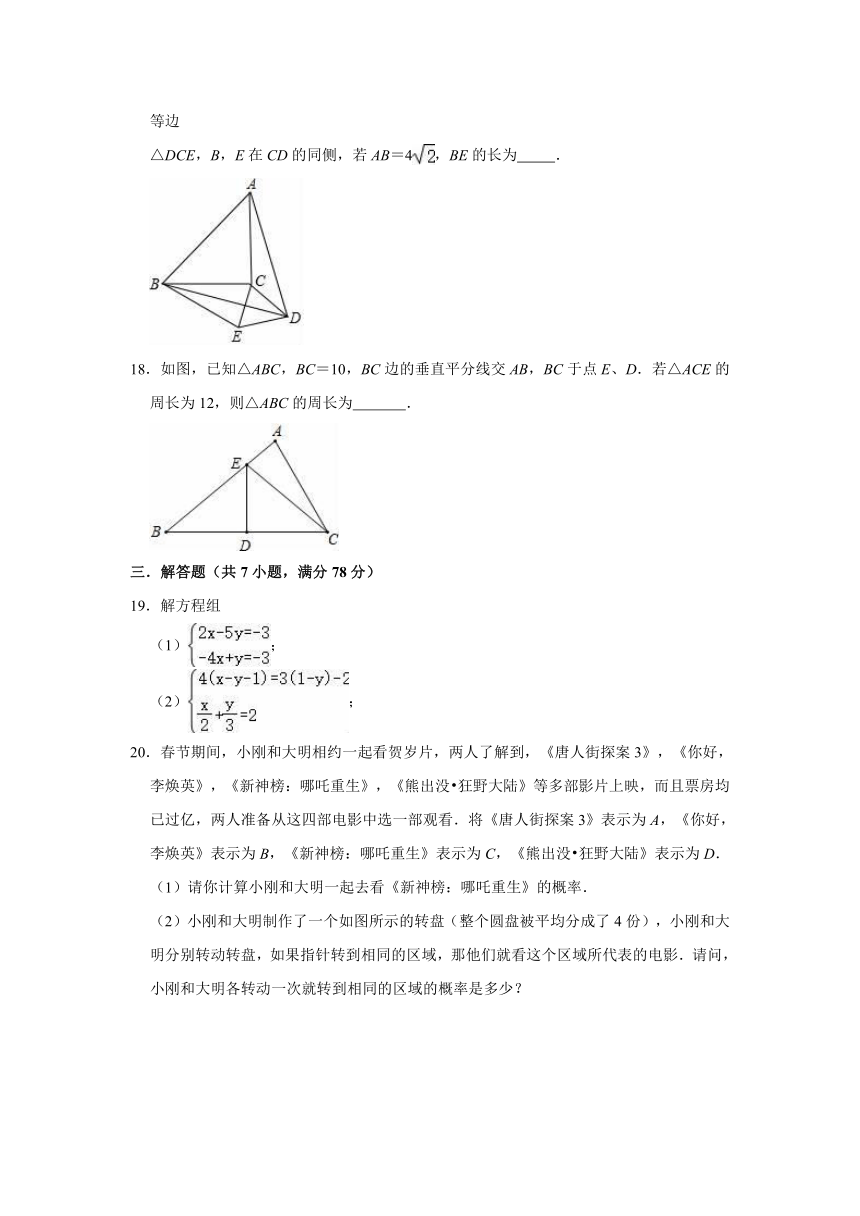
17.如图,以等腰直角三角形ABC的斜边AB为边作等边△ABD,连接DC,以DC为边作等边
△DCE,B,E在CD的同侧,若AB=4,BE的长为
.
18.如图,已知△ABC,BC=10,BC边的垂直平分线交AB,BC于点E、D.若△ACE的周长为12,则△ABC的周长为
.
三.解答题(共7小题,满分78分)
19.解方程组
(1);
(2);
20.春节期间,小刚和大明相约一起看贺岁片,两人了解到,《唐人街探案3》,《你好,李焕英》,《新神榜:哪吒重生》,《熊出没?狂野大陆》等多部影片上映,而且票房均已过亿,两人准备从这四部电影中选一部观看.将《唐人街探案3》表示为A,《你好,李焕英》表示为B,《新神榜:哪吒重生》表示为C,《熊出没?狂野大陆》表示为D.
(1)请你计算小刚和大明一起去看《新神榜:哪吒重生》的概率.
(2)小刚和大明制作了一个如图所示的转盘(整个圆盘被平均分成了4份),小刚和大明分别转动转盘,如果指针转到相同的区域,那他们就看这个区域所代表的电影.请问,小刚和大明各转动一次就转到相同的区域的概率是多少?
21.快车和慢车分别从A市和B市两地同时出发,匀速行驶,先相向而行,慢车到达A市后停止行驶,快车到达B市后,立即按原路原速度返回A市(调头时间忽略不计),结果与慢车同时到达A市.快、慢两车距B市的路程y1、y2(单位:km)与出发时间x(单位:h)之间的函数图象如图所示.
(1)A市和B市之间的路程是
km;
(2)求a的值,并解释图中点M的横坐标、纵坐标的实际意义;
(3)快车与慢车迎面相遇以后,再经过多长时间两车相距20km?
22.如图,在四边形ABCD中,BD⊥CD,EF⊥CD,且∠1=∠2.
(1)求证:AD∥BC;
(2)若BD平分∠ABC,∠A=130°,求∠C的度数.
23.已知:在△ABC中,∠ABC=90°,AB=BC,CD平分∠ACB,交AB于D,过B作BE⊥AC交AC于点E,交C的于点F.
(1)根据描述补全图形;
(2)试判断△BDF的形状,并说明理由;
(3)求证:.
24.在元旦期间,某商场投入13800元资金购进甲、乙两种商品共500件,两种商品的成本价和销售价如下表所示:
商品单价(元/件)
成本价
销售价
甲
24
36
乙
33
48
(1)该商场购进两种商品各多少件?
(2)这批商品全部销售完后,该商场共获利多少元?
25.已知:如图,△ABC中,∠C=90°,D为AB的中点,E、F分别在AC、BC上,且DE⊥DF.延长FD到G,使DG=DF,连接GE,GA.
求证:
(1)GE=FE
(2)∠EAG=90°
(3)AE2+BF2=EF2.
参考答案与试题解析
一.选择题(共12小题,满分48分,每小题4分)
1.解:根据概率的意义可得“抽到一等奖的概率为O.1”就是说抽10次可能抽到一等奖,也可能没有抽到一等奖,
故选:C.
2.解:A.符合二元一次方程组的定义,故本选项不合题意;
B.不符合二元一次方程组的定义,故本选项符合题意;
C.符合二元一次方程组的定义,故本选项不合题意;
D.符合二元一次方程组的定义,故本选项不合题意;
故选:B.
3.解:①由∠1=∠2,可得a∥b;
②由∠3+∠4=180°,可得a∥b;
③由∠5+∠6=180°,∠3+∠6=180°,可得∠5=∠3,即可得到a∥b;
④由∠2=∠3,不能得到a∥b;
⑤由∠7=∠2+∠3,∠7=∠1+∠3可得∠1=∠2,即可得到a∥b;
⑥由∠7+∠4﹣∠1=180°,∠7﹣∠1=∠3,可得∠3+∠4=180°,即可得到a∥b;
故选:C.
4.解:一个不透明的袋子中只装有5个红球,从中随机摸出一个球是黑球属于不可能事件;
故选:C.
5.解:①3cm是腰长时,三角形的三边分别为3cm、3cm、5cm,
能组成三角形,周长=3+3+5=11cm,
②3cm是底边长时,三角形的三边分别为3cm、5cm、5cm,
能组成三角形,周长=3+5+5=13cm,
综上所述,这个等腰三角形的周长是11cm或13cm.
故选:C.
6.解:延长DC交AB与G,延长CD交EF于H.
直角△BGC中,∠1=90°﹣α;
△EHD中,∠2=β﹣γ,
∵AB∥EF,
∴∠1=∠2,
∴90°﹣α=β﹣γ,
即α+β﹣γ=90°.
故选:B.
7.解:∠AOC=∠DAB﹣∠C=15°,
∴∠α=180°﹣15°=165°,
故选:D.
8.解:如图,∠3=∠1=50°,
∵a∥b,
∴∠2=∠3=50°.
故选:B.
9.解:∵直线y=3x+1经过点P(1,b),
∴b=3+1,
解得b=4,
∴P(1,4),
∴关于x,y的方程组的解为,
故选:C.
10.解:A.周长相等的三角形,形状不一定相同,大小不一定相等,所以不一定是全等三角形,故A错误;
B.面积相等的三角形,形状不一定相同,所以不一定完全重合,所以B错误;
C.形状相同大小相等的三角形能够完全重合,是全等三角形,故C正确;
D.所有的等边三角形形状相同,但是大小和边长有关,边长不相等,则不能够重合,所以D错误.
故选:C.
11.解:∵OP=1,OP1=,OP2=,OP3==2,
∴OP4==,
…,
OP2017=.
故选:D.
12.解:∵BE平分∠ABC,
∴∠ABE=∠CBE,
∵ED垂直平分AB,
∴EA=EB,
∴∠A=∠ABE,
∴∠A=∠ABE=∠CBE=×90°=30°,
在Rt△ABC中,BC=AC=×9=3,
在Rt△BCE中,CE=BC=×3=3,
∴BE=2CE=6,
∴AE=6.
故选:C.
二.填空题(共6小题,满分24分,每小题4分)
13.解:由题意得:,
解得,
再代入方程x+ay=2中得:
,
解得a=,
故答案为:.
14.解:设其中一双鞋分别为a,a′;
画树状图得:
∵共有12种情况,能配成一双的有8种情况,
∴取出两只刚好配一双鞋的概率是:=.
故答案为:.
15.解:因为第③块中有完整的两个角以及他们的夹边,利用ASA易证三角形全等,故应带第③块.
故答案为:③;
ASA.
16.解:∵∠1=∠2=∠3=54°,
∵∠1=∠5,
∴∠5=∠2,
∴l1∥l2,
∴∠6=∠3,
∴∠4=180°﹣∠6=180°﹣54°=126°,
故答案为:126°.
17.解:∵△ABD和△DCE是等边三角形,
∴BD=AD,ED=CD,
∵△ABC是等腰直角三角形,
∴AC=BC=AB=4,
在△ACD和△BCD中,,
∴△ACD≌△BCD(SSS),
∴∠ADC=∠BDC=30°,
∴∠BDE=60°﹣30°=30°,
在△BED和△ACD中,,
∴△BED≌△ACD(SAS),
∴BE=AC=4,
故答案为:4.
18.解:∵BC边的垂直平分线交AB,
∴BE=CE,
∵△ACE的周长为12,
∴AC+AE+CE=AC+AE+BE=AC+AB=12,
∵BC=10,
∴△ABC的周长为:AB+AC+BC=22.
故答案为:22.
三.解答题(共7小题,满分78分)
19.解:(1),
①×2+②得:﹣9y=﹣9,
解得:y=1,
把y=1代入②得:x=1,
则方程组的解为;
(2)方程组整理得:,
①×2+②得:11x=22,
解得:x=2,
把x=2代入①得:y=3,
则方程组的解为.
20.解:(1)列表如下:
A
B
C
D
A
(A,A)
(B,A)
(C,A)
(D,A)
B
(A,B)
(B,B)
(C,B)
(D,B)
C
(A,C)
(B,C)
(C,C)
(D,C)
D
(A,D)
(B,D)
(C,D)
(D,D)
由表知共有16种等可能结果,其中小刚和大明起去看《新神榜:哪吒重生》的只有1种结果,
∴小刚和大明起去看《新神榜:哪吒重生》的概率为;
(2)由表可知,小刚和大明各转动一次就转到相同的区域的有4种结果,
所以小刚和大明各转动一次就转到相同的区域的概率为=.
21.解:(1)由图可知,
A市和B市之间的路程是360km,
故答案为:360;
(2)根据题意可知快车速度是慢车速度的2倍,
设慢车速度为x
km/h,则快车速度为2x
km/h,
2(x+2x)=360,
解得,x=60
2×60=120,
则a=120,
点M的横坐标、纵坐标的实际意义是两车出发2小时时,在距B市120
km处相遇;
(3)快车速度为120
km/h,到达B市的时间为360÷120=3(h),
方法一:
当0≤x≤3时,y1=﹣120x+360,
当3<x≤6时,y1=120x﹣360,
y2=60x,
当0≤x≤3时,
y2﹣y1=20,即60x﹣(﹣120x+360)=20,
解得,x=,﹣2=,
当3<x≤6时,
y2﹣y1=20,即60x﹣(120x﹣360)=20,
解得,x=,﹣2=,
所以,快车与慢车迎面相遇以后,再经过或h两车相距20
km.
方法二:
设快车与慢车迎面相遇以后,再经过t
h两车相距20
km,
当0≤t≤3时,60t+120t=20,
解得,t=;
当3<t≤6时,60(t+2)﹣20=120(t+2)﹣360,
解得,t=.
所以,快车与慢车迎面相遇以后,再经过或h两车相距20
km.
22.解:(1)证明:如图,
∵BD⊥CD,EF⊥CD(已知),
∴BD∥EF(垂直于同一直线的两条直线平行),
∴∠2=∠3(两直线平行,同位角相等).
∵∠1=∠2,
∴∠1=∠3(等量代换).
∴AD∥BC(内错角相等,两直线平行).
(2)∵AD∥BC(已知),
∴∠ABC+∠A=180°(两直线平行,同旁内角互补).
∵∠A=130°(已知),
∴∠ABC=50°.
∵DB平分∠ABC(已知),
∴∠3=∠ABC=25°.
∴∠C=90°﹣∠3=65°.
23.解:(1)如图所示,
(2)△BDF为等腰三角形,
理由如下:∵∠ABC=90°,AB=BC,BE⊥AC,
∴∠ABE=∠CBE=∠A=∠BCA=45°,
∵CD平分∠BCA,
∴∠BCD=∠ACD=22.5°,
∴∠BFE=∠BDC=67.5,
∴BD=BF,
∴△BDF为等腰三角形;
(3)如图1,延长CB到H使BH=BF,
∵∠ABE=∠CBE=∠A=∠BCA=45°,
∴BE=EC=EA=,
∵∠ABC=90°,
∴∠HBD=90°,
∵BD=BF,
∴BD=BH,
∴∠H=∠BDH=45°,
在△ACD和△HCD中,
,
∴△ACD≌△HCD(AAS),
∴AC=CH,
∴BE=.
24.解:(1)设商场购进甲种商品x件,购进乙种商品y件,由题意得:
,
解得:,
答:商场购进甲种商品300件,购进乙种商品200件.
(2)根据题意得:
300×(36﹣24)+200×(48﹣33)
=3600+3000
=6600(元).
答:该商场共获得利润6600元.
25.证明:(1)∵DE⊥DF,DG=DF,
∴GE=FE;
(2)在△ADG与△BDF中,
,
∴△ADG≌△BDF(SAS),
∴AG=BF,∠GAD=∠FBD,
∴AG∥BC,
∴∠EAG=180°﹣∠C=90°;
(3)在Rt△AEG中,∵∠EAG=90°,
∴AE2+AG2=EG2,
∵AG=BF,EG=EF,
∴AE2+BF2=EF2.
一.选择题(共12小题,满分48分,每小题4分)
1.商场举行摸奖促销活动,对于“抽到一等奖的概率为0.1”.下列说法正确的是( )
A.抽10次奖必有一次抽到一等奖
B.抽一次不可能抽到一等奖
C.抽10次也可能没有抽到一等奖
D.抽了9次如果没有抽到一等奖,那么再抽一次肯定抽到一等奖
2.下列方程组中不是二元一次方程组的是( )
A.
B.
C.
D.
3.如图,下列条件:①∠1=∠2,②∠3+∠4=180°,③∠5+∠6=180°,④∠2=∠3,⑤∠7=∠2+∠3,⑥∠7+∠4﹣∠1=180°中能判断直线a∥b的有( )
A.3个
B.4个
C.5个
D.6个
4.一个不透明的袋子中只装有5个红球,从中随机摸出一个球是黑球( )
A.属于随机事件
B.可能性大小为
C.属于不可能事件
D.是必然事件
5.等腰三角形两边的长分别为3cm和5cm,则这个三角形的周长是( )
A.11cm
B.13cm
C.11cm或13cm
D.不确定
6.如图,AB∥EF,∠C=90°,则α、β、γ的关系为( )
A.β=α+γ
B.α+β﹣γ=90°
C.α+β+γ=180°
D.β+γ﹣α=90°
7.将一副直角三角板如图放置,使两直角边重合,则∠α的度数为( )
A.75°
B.105°
C.135°
D.165°
8.如图,直线l与直线a、b相交,且a∥b,∠1=50°,则∠2的度数是( )
A.130°
B.50°
C.100°
D.120°
9.如图,直线l1:y=3x+1与直线l2:y=mx+n相交于点P(1,b),则关于x,y的方程组的解为( )
A.
B.
C.
D.
10.下列说法正确的是( )
A.周长相等的三角形是全等三角形
B.全等三角形是指面积相等的三角形
C.全等三角形是指形状大小相等的三角形
D.所有的等边三角形都是全等三角形
11.如图,OP=1,过点P作PP1⊥OP且PP1=1,得OP1=;再过点P1作P1P2⊥OP1且P1P2=1,得OP2=;又过点P2作P2P3⊥OP2且P2P3=1,得OP3=2…依此法继续作下去,得OP2017=( )
A.
B.
C.
D.
12.如图,在Rt△ABC中,∠C=90°,BE平分∠ABC,ED垂直平分AB于D,若AC=9,则AE的值是( )
A.
B.
C.6
D.4
二.填空题(共6小题,满分24分,每小题4分)
13.若方程组的解也是二元一次方程x﹣y=1的一个解,则a=
.
14.有两双完全相同的鞋,从中任取两只,恰好成为一双的概率为
.
15.如图,黄芳不小心把一块三角形的玻璃打成三块碎片,现要带其中一块去配出与原来完全一样的玻璃,正确的办法是带来第
块去配,其依据是根据定理
(可以用字母简写)
16.已知:如图,∠1=∠2=∠3=54°,则∠4的度数是
.
17.如图,以等腰直角三角形ABC的斜边AB为边作等边△ABD,连接DC,以DC为边作等边
△DCE,B,E在CD的同侧,若AB=4,BE的长为
.
18.如图,已知△ABC,BC=10,BC边的垂直平分线交AB,BC于点E、D.若△ACE的周长为12,则△ABC的周长为
.
三.解答题(共7小题,满分78分)
19.解方程组
(1);
(2);
20.春节期间,小刚和大明相约一起看贺岁片,两人了解到,《唐人街探案3》,《你好,李焕英》,《新神榜:哪吒重生》,《熊出没?狂野大陆》等多部影片上映,而且票房均已过亿,两人准备从这四部电影中选一部观看.将《唐人街探案3》表示为A,《你好,李焕英》表示为B,《新神榜:哪吒重生》表示为C,《熊出没?狂野大陆》表示为D.
(1)请你计算小刚和大明一起去看《新神榜:哪吒重生》的概率.
(2)小刚和大明制作了一个如图所示的转盘(整个圆盘被平均分成了4份),小刚和大明分别转动转盘,如果指针转到相同的区域,那他们就看这个区域所代表的电影.请问,小刚和大明各转动一次就转到相同的区域的概率是多少?
21.快车和慢车分别从A市和B市两地同时出发,匀速行驶,先相向而行,慢车到达A市后停止行驶,快车到达B市后,立即按原路原速度返回A市(调头时间忽略不计),结果与慢车同时到达A市.快、慢两车距B市的路程y1、y2(单位:km)与出发时间x(单位:h)之间的函数图象如图所示.
(1)A市和B市之间的路程是
km;
(2)求a的值,并解释图中点M的横坐标、纵坐标的实际意义;
(3)快车与慢车迎面相遇以后,再经过多长时间两车相距20km?
22.如图,在四边形ABCD中,BD⊥CD,EF⊥CD,且∠1=∠2.
(1)求证:AD∥BC;
(2)若BD平分∠ABC,∠A=130°,求∠C的度数.
23.已知:在△ABC中,∠ABC=90°,AB=BC,CD平分∠ACB,交AB于D,过B作BE⊥AC交AC于点E,交C的于点F.
(1)根据描述补全图形;
(2)试判断△BDF的形状,并说明理由;
(3)求证:.
24.在元旦期间,某商场投入13800元资金购进甲、乙两种商品共500件,两种商品的成本价和销售价如下表所示:
商品单价(元/件)
成本价
销售价
甲
24
36
乙
33
48
(1)该商场购进两种商品各多少件?
(2)这批商品全部销售完后,该商场共获利多少元?
25.已知:如图,△ABC中,∠C=90°,D为AB的中点,E、F分别在AC、BC上,且DE⊥DF.延长FD到G,使DG=DF,连接GE,GA.
求证:
(1)GE=FE
(2)∠EAG=90°
(3)AE2+BF2=EF2.
参考答案与试题解析
一.选择题(共12小题,满分48分,每小题4分)
1.解:根据概率的意义可得“抽到一等奖的概率为O.1”就是说抽10次可能抽到一等奖,也可能没有抽到一等奖,
故选:C.
2.解:A.符合二元一次方程组的定义,故本选项不合题意;
B.不符合二元一次方程组的定义,故本选项符合题意;
C.符合二元一次方程组的定义,故本选项不合题意;
D.符合二元一次方程组的定义,故本选项不合题意;
故选:B.
3.解:①由∠1=∠2,可得a∥b;
②由∠3+∠4=180°,可得a∥b;
③由∠5+∠6=180°,∠3+∠6=180°,可得∠5=∠3,即可得到a∥b;
④由∠2=∠3,不能得到a∥b;
⑤由∠7=∠2+∠3,∠7=∠1+∠3可得∠1=∠2,即可得到a∥b;
⑥由∠7+∠4﹣∠1=180°,∠7﹣∠1=∠3,可得∠3+∠4=180°,即可得到a∥b;
故选:C.
4.解:一个不透明的袋子中只装有5个红球,从中随机摸出一个球是黑球属于不可能事件;
故选:C.
5.解:①3cm是腰长时,三角形的三边分别为3cm、3cm、5cm,
能组成三角形,周长=3+3+5=11cm,
②3cm是底边长时,三角形的三边分别为3cm、5cm、5cm,
能组成三角形,周长=3+5+5=13cm,
综上所述,这个等腰三角形的周长是11cm或13cm.
故选:C.
6.解:延长DC交AB与G,延长CD交EF于H.
直角△BGC中,∠1=90°﹣α;
△EHD中,∠2=β﹣γ,
∵AB∥EF,
∴∠1=∠2,
∴90°﹣α=β﹣γ,
即α+β﹣γ=90°.
故选:B.
7.解:∠AOC=∠DAB﹣∠C=15°,
∴∠α=180°﹣15°=165°,
故选:D.
8.解:如图,∠3=∠1=50°,
∵a∥b,
∴∠2=∠3=50°.
故选:B.
9.解:∵直线y=3x+1经过点P(1,b),
∴b=3+1,
解得b=4,
∴P(1,4),
∴关于x,y的方程组的解为,
故选:C.
10.解:A.周长相等的三角形,形状不一定相同,大小不一定相等,所以不一定是全等三角形,故A错误;
B.面积相等的三角形,形状不一定相同,所以不一定完全重合,所以B错误;
C.形状相同大小相等的三角形能够完全重合,是全等三角形,故C正确;
D.所有的等边三角形形状相同,但是大小和边长有关,边长不相等,则不能够重合,所以D错误.
故选:C.
11.解:∵OP=1,OP1=,OP2=,OP3==2,
∴OP4==,
…,
OP2017=.
故选:D.
12.解:∵BE平分∠ABC,
∴∠ABE=∠CBE,
∵ED垂直平分AB,
∴EA=EB,
∴∠A=∠ABE,
∴∠A=∠ABE=∠CBE=×90°=30°,
在Rt△ABC中,BC=AC=×9=3,
在Rt△BCE中,CE=BC=×3=3,
∴BE=2CE=6,
∴AE=6.
故选:C.
二.填空题(共6小题,满分24分,每小题4分)
13.解:由题意得:,
解得,
再代入方程x+ay=2中得:
,
解得a=,
故答案为:.
14.解:设其中一双鞋分别为a,a′;
画树状图得:
∵共有12种情况,能配成一双的有8种情况,
∴取出两只刚好配一双鞋的概率是:=.
故答案为:.
15.解:因为第③块中有完整的两个角以及他们的夹边,利用ASA易证三角形全等,故应带第③块.
故答案为:③;
ASA.
16.解:∵∠1=∠2=∠3=54°,
∵∠1=∠5,
∴∠5=∠2,
∴l1∥l2,
∴∠6=∠3,
∴∠4=180°﹣∠6=180°﹣54°=126°,
故答案为:126°.
17.解:∵△ABD和△DCE是等边三角形,
∴BD=AD,ED=CD,
∵△ABC是等腰直角三角形,
∴AC=BC=AB=4,
在△ACD和△BCD中,,
∴△ACD≌△BCD(SSS),
∴∠ADC=∠BDC=30°,
∴∠BDE=60°﹣30°=30°,
在△BED和△ACD中,,
∴△BED≌△ACD(SAS),
∴BE=AC=4,
故答案为:4.
18.解:∵BC边的垂直平分线交AB,
∴BE=CE,
∵△ACE的周长为12,
∴AC+AE+CE=AC+AE+BE=AC+AB=12,
∵BC=10,
∴△ABC的周长为:AB+AC+BC=22.
故答案为:22.
三.解答题(共7小题,满分78分)
19.解:(1),
①×2+②得:﹣9y=﹣9,
解得:y=1,
把y=1代入②得:x=1,
则方程组的解为;
(2)方程组整理得:,
①×2+②得:11x=22,
解得:x=2,
把x=2代入①得:y=3,
则方程组的解为.
20.解:(1)列表如下:
A
B
C
D
A
(A,A)
(B,A)
(C,A)
(D,A)
B
(A,B)
(B,B)
(C,B)
(D,B)
C
(A,C)
(B,C)
(C,C)
(D,C)
D
(A,D)
(B,D)
(C,D)
(D,D)
由表知共有16种等可能结果,其中小刚和大明起去看《新神榜:哪吒重生》的只有1种结果,
∴小刚和大明起去看《新神榜:哪吒重生》的概率为;
(2)由表可知,小刚和大明各转动一次就转到相同的区域的有4种结果,
所以小刚和大明各转动一次就转到相同的区域的概率为=.
21.解:(1)由图可知,
A市和B市之间的路程是360km,
故答案为:360;
(2)根据题意可知快车速度是慢车速度的2倍,
设慢车速度为x
km/h,则快车速度为2x
km/h,
2(x+2x)=360,
解得,x=60
2×60=120,
则a=120,
点M的横坐标、纵坐标的实际意义是两车出发2小时时,在距B市120
km处相遇;
(3)快车速度为120
km/h,到达B市的时间为360÷120=3(h),
方法一:
当0≤x≤3时,y1=﹣120x+360,
当3<x≤6时,y1=120x﹣360,
y2=60x,
当0≤x≤3时,
y2﹣y1=20,即60x﹣(﹣120x+360)=20,
解得,x=,﹣2=,
当3<x≤6时,
y2﹣y1=20,即60x﹣(120x﹣360)=20,
解得,x=,﹣2=,
所以,快车与慢车迎面相遇以后,再经过或h两车相距20
km.
方法二:
设快车与慢车迎面相遇以后,再经过t
h两车相距20
km,
当0≤t≤3时,60t+120t=20,
解得,t=;
当3<t≤6时,60(t+2)﹣20=120(t+2)﹣360,
解得,t=.
所以,快车与慢车迎面相遇以后,再经过或h两车相距20
km.
22.解:(1)证明:如图,
∵BD⊥CD,EF⊥CD(已知),
∴BD∥EF(垂直于同一直线的两条直线平行),
∴∠2=∠3(两直线平行,同位角相等).
∵∠1=∠2,
∴∠1=∠3(等量代换).
∴AD∥BC(内错角相等,两直线平行).
(2)∵AD∥BC(已知),
∴∠ABC+∠A=180°(两直线平行,同旁内角互补).
∵∠A=130°(已知),
∴∠ABC=50°.
∵DB平分∠ABC(已知),
∴∠3=∠ABC=25°.
∴∠C=90°﹣∠3=65°.
23.解:(1)如图所示,
(2)△BDF为等腰三角形,
理由如下:∵∠ABC=90°,AB=BC,BE⊥AC,
∴∠ABE=∠CBE=∠A=∠BCA=45°,
∵CD平分∠BCA,
∴∠BCD=∠ACD=22.5°,
∴∠BFE=∠BDC=67.5,
∴BD=BF,
∴△BDF为等腰三角形;
(3)如图1,延长CB到H使BH=BF,
∵∠ABE=∠CBE=∠A=∠BCA=45°,
∴BE=EC=EA=,
∵∠ABC=90°,
∴∠HBD=90°,
∵BD=BF,
∴BD=BH,
∴∠H=∠BDH=45°,
在△ACD和△HCD中,
,
∴△ACD≌△HCD(AAS),
∴AC=CH,
∴BE=.
24.解:(1)设商场购进甲种商品x件,购进乙种商品y件,由题意得:
,
解得:,
答:商场购进甲种商品300件,购进乙种商品200件.
(2)根据题意得:
300×(36﹣24)+200×(48﹣33)
=3600+3000
=6600(元).
答:该商场共获得利润6600元.
25.证明:(1)∵DE⊥DF,DG=DF,
∴GE=FE;
(2)在△ADG与△BDF中,
,
∴△ADG≌△BDF(SAS),
∴AG=BF,∠GAD=∠FBD,
∴AG∥BC,
∴∠EAG=180°﹣∠C=90°;
(3)在Rt△AEG中,∵∠EAG=90°,
∴AE2+AG2=EG2,
∵AG=BF,EG=EF,
∴AE2+BF2=EF2.
同课章节目录
