六年级数学下册课件-4.4圆锥和圆锥的体积公式 冀教版(共23张PPT)
文档属性
| 名称 | 六年级数学下册课件-4.4圆锥和圆锥的体积公式 冀教版(共23张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 968.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-29 00:00:00 | ||
图片预览








文档简介
(共23张PPT)
冀教版六年级下册第四单元第7课时
圆锥和圆锥的体积公式
一、复习旧知
我们已经学过了圆柱,回想一下:你知道圆柱的哪些知识?
二、导入新课
在日常生活中,大家见过类似陀螺的物品吗?请举例。
大家观察这些实物照片,它们都有哪些相同的特性?
顶端尖尖的,底面圆圆的,
顶端到底面圆心的距离是垂直的,
侧面是一个曲面??????
像这样的物体我们称为“圆锥”,这节课我们来学习圆锥和圆锥的体积公式。
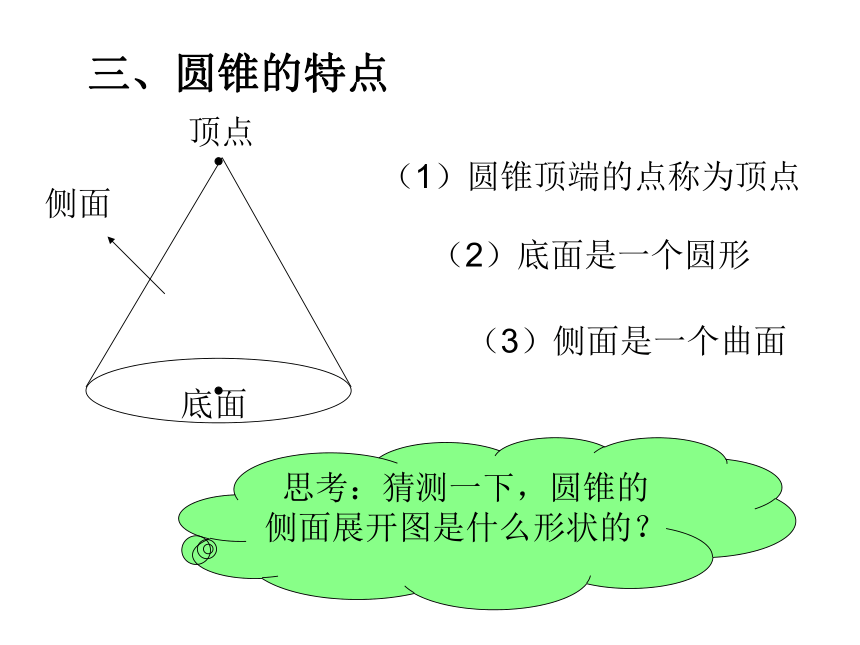
三、圆锥的特点
(1)圆锥顶端的点称为顶点
(2)底面是一个圆形
(3)侧面是一个曲面
顶点
底面
侧面
思考:猜测一下,圆锥的侧面展开图是什么形状的?
尝试动手折一折,围一围,看最后是
什么形状的纸可围成圆锥?
(4)只有扇形的纸可围成圆锥,即圆锥的侧面展开图是扇形。
拿出每小组分发的纸片:
(5)认识圆锥的高:
┇┇┇┇┇┇┇
┇┇┇┇┇┇┇
┇┇┇┇┇┇┇┇┇┇┇┇┇
从圆锥顶点到底面圆心的距离叫做圆锥的高。
圆锥只有一条高。
┆┆┆┆┆┆┆┆┆
四、圆锥体积公式的推导
若下面这两个圆锥里装满奶油,哪个装的奶油多呢?
还需要知道两个圆锥的体积的大小。
探究圆锥的体积:
(1)拿出事先准备的实验用品,观察你手中的圆柱和圆锥,它们有什么关系?你怎样知道的?
圆柱和圆锥等底等高
思考:猜测一下,若把圆锥装满沙土,倒几次才能把圆柱装满?
实验要求:
(1)把圆锥形容器中装满沙子,然后倒入圆柱中,看几次倒满。
(2)边实验边填写实验记录表。
(3)尝试把圆柱形容器中装满沙土,倒入圆锥中,能装满几个圆锥。
实验记录
第一次
第二次
圆柱形容器中沙子的高度(厘米)
实验结论:_____________________
’
实验工具:
圆锥形容器、圆柱形容器
高:____
实验过程记录:
实验得到的数据有一定的误差,是在允许的范围内。大家通过做实验得到什么结论?
在等底等高情况下,圆柱体积是圆锥的3倍,也就是说,圆锥体积是和它等底等高圆柱体积的
观察数据,为何会不一样?
请尝试推导出圆锥体积公式:
(注意:圆锥与圆柱在等底等高情况下)
圆柱体积=底面积×高
圆锥体积=圆柱体积×
=底面积×高×
若用V表示圆锥的体积,S表示圆锥的底面积,h表示圆锥的高
,那么圆锥体积的字母公式是:V=
Sh
V=
π
h
四、圆锥体积公式的应用
1、计算下面各圆锥体积
(1)
┆┆┆┆┆┆┆┆┆┆
S=9.6平方米
2米
=
×
19.2
×9.6×2
=
6.4(立方米)
(2)
×3.14××12
=
3.14
×
25
×4
=
314(立方分米)
12分米
5分米
(2)
(3)
┆┆┆┆┆┆┆┆┆┆
12厘米
15厘米
3.14×
6
×
6
×15×
=3.14×36×5
=113.04×5
=565.2(立方厘米)
12÷2=6(厘米)
18÷2=9(厘米)
3.14×
×15×(1-
)
=3.14×81×15×
=254.34×10
=2543.4(立方厘米)
2、如下图,把这个圆柱削成一个最大的圆锥,那么削去部分的体积是多少?
18厘米
15厘米
3、如果一个圆柱和一个圆锥底面积相等,圆柱的高是圆锥的高的3倍,那么圆柱的体积是圆锥体积的()倍。
分析:V柱÷
V锥
=
Sh柱÷(
Sh锥)
=
S×(h锥×3)÷(
Sh锥)
=3÷
=9
六、课堂小结:
这节课,大家学到了哪些知识?
七、布置作业:
1、数学书第42页,1、2、3、4
2、基本功第23页
。
谢谢!希望对你有所帮助。
冀教版六年级下册第四单元第7课时
圆锥和圆锥的体积公式
一、复习旧知
我们已经学过了圆柱,回想一下:你知道圆柱的哪些知识?
二、导入新课
在日常生活中,大家见过类似陀螺的物品吗?请举例。
大家观察这些实物照片,它们都有哪些相同的特性?
顶端尖尖的,底面圆圆的,
顶端到底面圆心的距离是垂直的,
侧面是一个曲面??????
像这样的物体我们称为“圆锥”,这节课我们来学习圆锥和圆锥的体积公式。
三、圆锥的特点
(1)圆锥顶端的点称为顶点
(2)底面是一个圆形
(3)侧面是一个曲面
顶点
底面
侧面
思考:猜测一下,圆锥的侧面展开图是什么形状的?
尝试动手折一折,围一围,看最后是
什么形状的纸可围成圆锥?
(4)只有扇形的纸可围成圆锥,即圆锥的侧面展开图是扇形。
拿出每小组分发的纸片:
(5)认识圆锥的高:
┇┇┇┇┇┇┇
┇┇┇┇┇┇┇
┇┇┇┇┇┇┇┇┇┇┇┇┇
从圆锥顶点到底面圆心的距离叫做圆锥的高。
圆锥只有一条高。
┆┆┆┆┆┆┆┆┆
四、圆锥体积公式的推导
若下面这两个圆锥里装满奶油,哪个装的奶油多呢?
还需要知道两个圆锥的体积的大小。
探究圆锥的体积:
(1)拿出事先准备的实验用品,观察你手中的圆柱和圆锥,它们有什么关系?你怎样知道的?
圆柱和圆锥等底等高
思考:猜测一下,若把圆锥装满沙土,倒几次才能把圆柱装满?
实验要求:
(1)把圆锥形容器中装满沙子,然后倒入圆柱中,看几次倒满。
(2)边实验边填写实验记录表。
(3)尝试把圆柱形容器中装满沙土,倒入圆锥中,能装满几个圆锥。
实验记录
第一次
第二次
圆柱形容器中沙子的高度(厘米)
实验结论:_____________________
’
实验工具:
圆锥形容器、圆柱形容器
高:____
实验过程记录:
实验得到的数据有一定的误差,是在允许的范围内。大家通过做实验得到什么结论?
在等底等高情况下,圆柱体积是圆锥的3倍,也就是说,圆锥体积是和它等底等高圆柱体积的
观察数据,为何会不一样?
请尝试推导出圆锥体积公式:
(注意:圆锥与圆柱在等底等高情况下)
圆柱体积=底面积×高
圆锥体积=圆柱体积×
=底面积×高×
若用V表示圆锥的体积,S表示圆锥的底面积,h表示圆锥的高
,那么圆锥体积的字母公式是:V=
Sh
V=
π
h
四、圆锥体积公式的应用
1、计算下面各圆锥体积
(1)
┆┆┆┆┆┆┆┆┆┆
S=9.6平方米
2米
=
×
19.2
×9.6×2
=
6.4(立方米)
(2)
×3.14××12
=
3.14
×
25
×4
=
314(立方分米)
12分米
5分米
(2)
(3)
┆┆┆┆┆┆┆┆┆┆
12厘米
15厘米
3.14×
6
×
6
×15×
=3.14×36×5
=113.04×5
=565.2(立方厘米)
12÷2=6(厘米)
18÷2=9(厘米)
3.14×
×15×(1-
)
=3.14×81×15×
=254.34×10
=2543.4(立方厘米)
2、如下图,把这个圆柱削成一个最大的圆锥,那么削去部分的体积是多少?
18厘米
15厘米
3、如果一个圆柱和一个圆锥底面积相等,圆柱的高是圆锥的高的3倍,那么圆柱的体积是圆锥体积的()倍。
分析:V柱÷
V锥
=
Sh柱÷(
Sh锥)
=
S×(h锥×3)÷(
Sh锥)
=3÷
=9
六、课堂小结:
这节课,大家学到了哪些知识?
七、布置作业:
1、数学书第42页,1、2、3、4
2、基本功第23页
。
谢谢!希望对你有所帮助。
