江西省贵溪市高中2020-2021学年高一下学期第三次月考(5月)数学试题(三校生) Word版含答案
文档属性
| 名称 | 江西省贵溪市高中2020-2021学年高一下学期第三次月考(5月)数学试题(三校生) Word版含答案 |  | |
| 格式 | doc | ||
| 文件大小 | 562.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-29 12:24:06 | ||
图片预览




文档简介
贵溪市高中2020-2021学年第二学期第三次月考
高一三校生数学试卷
考试时间:120分钟 试卷分值:150分 命题人:
一、是非选择题:本大题共10小题,每小题3分,共30分。对每小题的命题作出判断,对的选A,错的选B。
1. 空间中有三条线段AB,BC,CD,且,那么直线AB与CD的位置关系是平行
2. 过平面外两点一定能作该平面的平行平面
3. 已知平面α内有无数条直线都与平面β平行,那么α∥β
4. 设是两条不同的直线,是两个不同的平面,若则
5. 若点Q在直线b上,b在平面内,则
6. 在等差数列中,则9
7. 已知直线平面,则直线平面是直线的充要条件
8. 平面∥平面,,则直线和的位置关系平行或相交
9. 不等式的解集是
10. 设等差数列的前n项和为,且,,则9
二、单项选择题:本大题共8小题,每小题5分,共40分。
11.下图是由哪个平面图形旋转得到的( )
A. B. C. D.
12.设集合,,则( )
A. B. C. D.
13.已知空间四边形的四边长相等,则顺次连接各边中点形成的四边形是.
A.梯形 B.菱形 C.矩形 D.正方形
14.已知在中,,,,则的值为
A. B. C.8 D.10
15.设等差数列的前项和为,已知,则.
A. B. C. D.
16.在递增等比数列中,,则( )
A. B.2 C.4 D.8
17.已知公比为2的等比数列中,,则
A.12 B.18 C.24 D.6
18.若关于的不等式的解集为,则实数的值是( )
A.1 B.2 C.3 D.4
填空题:本大题共6小题,每小题5分,共30分。
19.函数()的最小值为____________
20.在△ABC中,若b=1,A=60°,△ABC的面积为,则a=_____.
21.如图,已知PA⊥平面ABC,BC⊥AC,则图中直角三角形的个数为________.
22.三个平面会把空间分割成_________个部分(答出所有可能得分).
23.一条直线上的3个点到平面的距离为1,这条直线和平面的关系是____________.
24.已知平面α,直线m,n满足mα,nα,则“m∥n”是“m∥α”的__________条件
解答题:本大题共6小题,25-28小题每小题8分,29-30小题每小题9分,共50分。解答应写出过程或步骤。
25.解下列不等式:
(1)
(2)
26.已知正方体,
(1)证明:平面;
(2)求异面直线与所成的角.
27.为等差数列的前项和,已知,.
(1)求数列的通项公式;
(2)求,并求的最小值.
28.如图,四面体ABCD中,O、E分别是BD、BC的中点,
求证:平面BCD;
29.(本题满分12分)
在△ABC中,角A,B,C的对边分别是a,b,c,已知
(1)求的值;
(2)若,求边c的值.
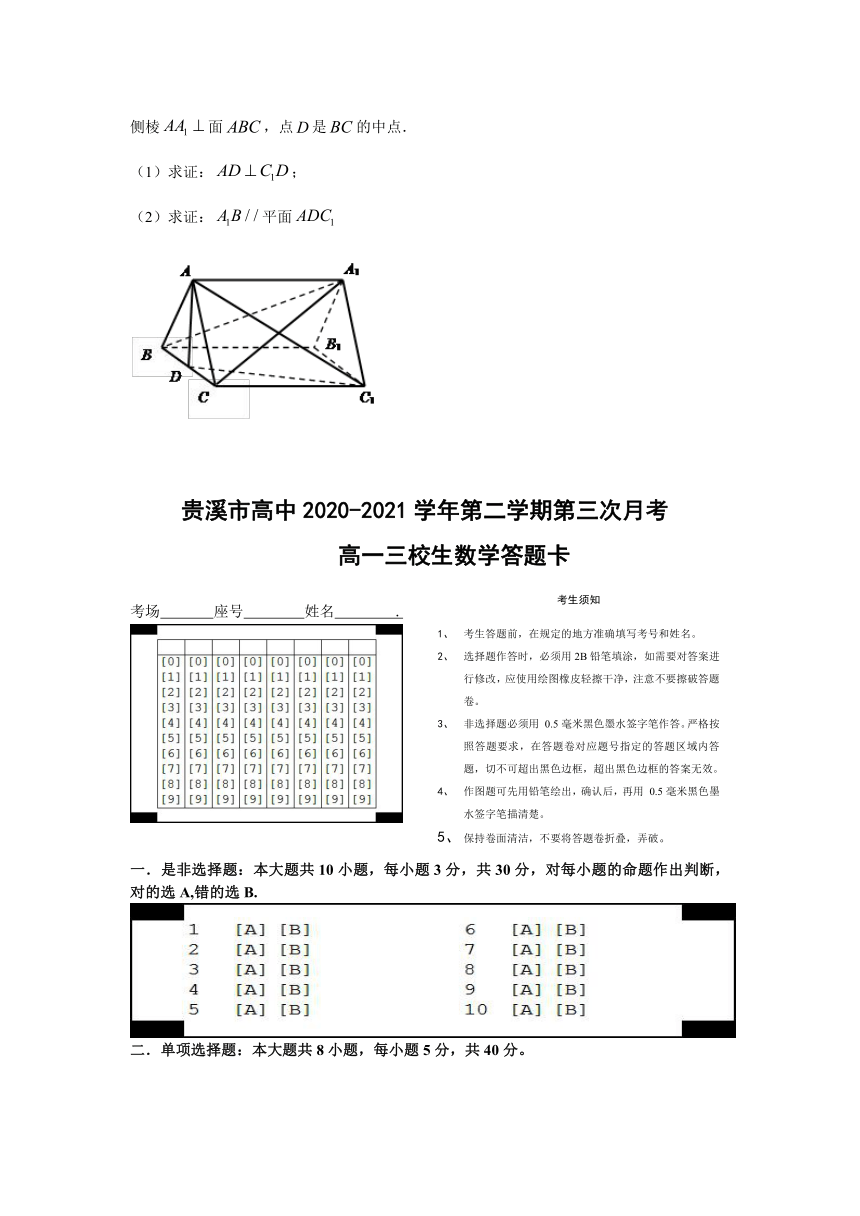
30.如图,在三棱柱中,底面是边长为2的正三角形,侧棱长为3,且侧棱面,点是的中点.
(1)求证:;
(2)求证:平面
贵溪市高中2020-2021学年第二学期第三次月考 高一三校生数学答题卡
考场 座号 姓名 .
考生须知
考生答题前,在规定的地方准确填写考号和姓名。
选择题作答时,必须用2B铅笔填涂,如需要对答案进行修改,应使用绘图橡皮轻擦干净,注意不要擦破答题卷。
非选择题必须用 0.5毫米黑色墨水签字笔作答。严格按照答题要求,在答题卷对应题号指定的答题区域内答题,切不可超出黑色边框,超出黑色边框的答案无效。
作图题可先用铅笔绘出,确认后,再用 0.5毫米黑色墨水签字笔描清楚。
保持卷面清洁,不要将答题卷折叠,弄破。
一.是非选择题:本大题共10小题,每小题3分,共30分,对每小题的命题作出判断,对的选A,错的选B.
二.单项选择题:本大题共8小题,每小题5分,共40分。
三、填空题:本大题共6小题,每小题5分,共30分
19、 20、 21、 ;
22、 23、 24、 ;
四、解答题:本大题共6小题,25——28小题每小题8分,29——30小题每小题9分,共50分,解答应写出过程或步骤
25(8分)
26(8分)
27(8分)
28(8分)
29(9分)
30(9分)
贵溪市高中2020-2021学年第二学期第三次月考
高一三 校 生 数 学 答 案
一.是非选择题
题号 1 2 3 4 5 6 7 8 9 10
答案 B B B A B A B B A A
二、单项选择题
题号 11 12 13 14 15 16 17 18
答案 A B C A C B C A
填空题
0 20. 21. 4
4,或6,或7,或8 23.平行 24. 平行
解答题
25. (1)令,解得:或
的解集为
(2)由得:,解得:
的解集为
26. (1)证:在正方体中,
,且,
∴四边形为平行四边形,
∴,
又∵平面,平面;
∴平面;
(2)解:∵,
∴即为异面直线与所成的角,
设正方体的边长为,
则易得,
∴为等边三角形,
∴,
故异面直线与所成的角为.
27. (1)设的公差为 ,
由,,
即,解得,
所以.
(2),
,
所以当时,的最小值为.
28. 证明:为的中点,,
,,,,
又,,
,均在平面内,平面
29. (1)由及正弦定理得
,即.
∵
∴,即.
∵
∴
(2)由及,得.
∴
∵
∴,即,即得.
∵
∴
∴或
∴或.
若,则,在直角中,,解得;
若,在直角中,,解得.
30. (1)因为三棱柱是正三棱柱,所以面,
又面,所以,
又点是的中点,且为正三角形,所以,
因为,所以平面,
又因为平面,所以.
(2) 连接交于点,再连接.
因为四边形为矩形,
所以为的中点,
又因为为的中点,
所以,
又平面,平面,
所以平面.
高一三校生数学试卷
考试时间:120分钟 试卷分值:150分 命题人:
一、是非选择题:本大题共10小题,每小题3分,共30分。对每小题的命题作出判断,对的选A,错的选B。
1. 空间中有三条线段AB,BC,CD,且,那么直线AB与CD的位置关系是平行
2. 过平面外两点一定能作该平面的平行平面
3. 已知平面α内有无数条直线都与平面β平行,那么α∥β
4. 设是两条不同的直线,是两个不同的平面,若则
5. 若点Q在直线b上,b在平面内,则
6. 在等差数列中,则9
7. 已知直线平面,则直线平面是直线的充要条件
8. 平面∥平面,,则直线和的位置关系平行或相交
9. 不等式的解集是
10. 设等差数列的前n项和为,且,,则9
二、单项选择题:本大题共8小题,每小题5分,共40分。
11.下图是由哪个平面图形旋转得到的( )
A. B. C. D.
12.设集合,,则( )
A. B. C. D.
13.已知空间四边形的四边长相等,则顺次连接各边中点形成的四边形是.
A.梯形 B.菱形 C.矩形 D.正方形
14.已知在中,,,,则的值为
A. B. C.8 D.10
15.设等差数列的前项和为,已知,则.
A. B. C. D.
16.在递增等比数列中,,则( )
A. B.2 C.4 D.8
17.已知公比为2的等比数列中,,则
A.12 B.18 C.24 D.6
18.若关于的不等式的解集为,则实数的值是( )
A.1 B.2 C.3 D.4
填空题:本大题共6小题,每小题5分,共30分。
19.函数()的最小值为____________
20.在△ABC中,若b=1,A=60°,△ABC的面积为,则a=_____.
21.如图,已知PA⊥平面ABC,BC⊥AC,则图中直角三角形的个数为________.
22.三个平面会把空间分割成_________个部分(答出所有可能得分).
23.一条直线上的3个点到平面的距离为1,这条直线和平面的关系是____________.
24.已知平面α,直线m,n满足mα,nα,则“m∥n”是“m∥α”的__________条件
解答题:本大题共6小题,25-28小题每小题8分,29-30小题每小题9分,共50分。解答应写出过程或步骤。
25.解下列不等式:
(1)
(2)
26.已知正方体,
(1)证明:平面;
(2)求异面直线与所成的角.
27.为等差数列的前项和,已知,.
(1)求数列的通项公式;
(2)求,并求的最小值.
28.如图,四面体ABCD中,O、E分别是BD、BC的中点,
求证:平面BCD;
29.(本题满分12分)
在△ABC中,角A,B,C的对边分别是a,b,c,已知
(1)求的值;
(2)若,求边c的值.
30.如图,在三棱柱中,底面是边长为2的正三角形,侧棱长为3,且侧棱面,点是的中点.
(1)求证:;
(2)求证:平面
贵溪市高中2020-2021学年第二学期第三次月考 高一三校生数学答题卡
考场 座号 姓名 .
考生须知
考生答题前,在规定的地方准确填写考号和姓名。
选择题作答时,必须用2B铅笔填涂,如需要对答案进行修改,应使用绘图橡皮轻擦干净,注意不要擦破答题卷。
非选择题必须用 0.5毫米黑色墨水签字笔作答。严格按照答题要求,在答题卷对应题号指定的答题区域内答题,切不可超出黑色边框,超出黑色边框的答案无效。
作图题可先用铅笔绘出,确认后,再用 0.5毫米黑色墨水签字笔描清楚。
保持卷面清洁,不要将答题卷折叠,弄破。
一.是非选择题:本大题共10小题,每小题3分,共30分,对每小题的命题作出判断,对的选A,错的选B.
二.单项选择题:本大题共8小题,每小题5分,共40分。
三、填空题:本大题共6小题,每小题5分,共30分
19、 20、 21、 ;
22、 23、 24、 ;
四、解答题:本大题共6小题,25——28小题每小题8分,29——30小题每小题9分,共50分,解答应写出过程或步骤
25(8分)
26(8分)
27(8分)
28(8分)
29(9分)
30(9分)
贵溪市高中2020-2021学年第二学期第三次月考
高一三 校 生 数 学 答 案
一.是非选择题
题号 1 2 3 4 5 6 7 8 9 10
答案 B B B A B A B B A A
二、单项选择题
题号 11 12 13 14 15 16 17 18
答案 A B C A C B C A
填空题
0 20. 21. 4
4,或6,或7,或8 23.平行 24. 平行
解答题
25. (1)令,解得:或
的解集为
(2)由得:,解得:
的解集为
26. (1)证:在正方体中,
,且,
∴四边形为平行四边形,
∴,
又∵平面,平面;
∴平面;
(2)解:∵,
∴即为异面直线与所成的角,
设正方体的边长为,
则易得,
∴为等边三角形,
∴,
故异面直线与所成的角为.
27. (1)设的公差为 ,
由,,
即,解得,
所以.
(2),
,
所以当时,的最小值为.
28. 证明:为的中点,,
,,,,
又,,
,均在平面内,平面
29. (1)由及正弦定理得
,即.
∵
∴,即.
∵
∴
(2)由及,得.
∴
∵
∴,即,即得.
∵
∴
∴或
∴或.
若,则,在直角中,,解得;
若,在直角中,,解得.
30. (1)因为三棱柱是正三棱柱,所以面,
又面,所以,
又点是的中点,且为正三角形,所以,
因为,所以平面,
又因为平面,所以.
(2) 连接交于点,再连接.
因为四边形为矩形,
所以为的中点,
又因为为的中点,
所以,
又平面,平面,
所以平面.
同课章节目录
