真分数型不等式的证明及其应用

(共14张PPT)
真分数型不等式及应用
一、创设情景 提出问题
给b克糖水（其中含有糖a克）加入糖m克，能使糖水变甜,你能把这一生活常识用一个不等式表达出来吗？
加糖前的糖的浓度 （<或>）加糖后
的浓度。加糖前的浓度表达式是（ ）
加糖后的浓度表达式是( ),所以可以得到真分数不等式：
分析：
<
二、合作交流 感知问题
观察该不等式的结构特征，想想除了用比较法、分析法外，你还能用几种方法来证明它？
思路一：由不等式两边都是分式形式，可寻觅到这个式子隐含的几何背景——直线的斜率：
在直角坐标系中，
表示经过A(b,a)和B(-m,-m)两点所成直线的斜率，记倾斜角为
表示过原点O(0,0)和点A(b,a)的直线的斜率
设直线AO的倾斜角为
二、合作交流 感知问题
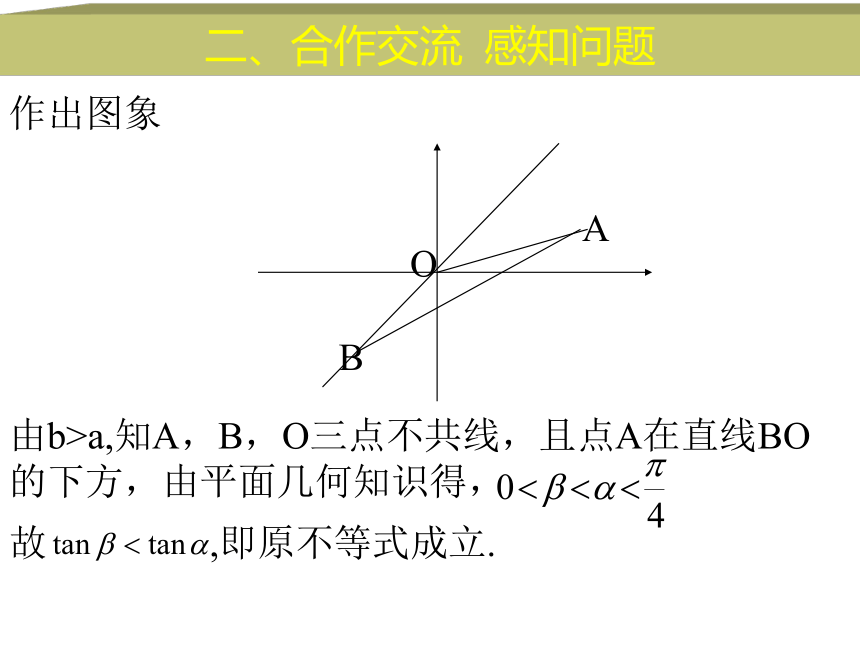
作出图象
A
B
O
由b>a,知A，B，O三点不共线，且点A在直线BO的下方，由平面几何知识得，
故 ,即原不等式成立.
二、合作交流 感知问题
思路二：注意到 把式子中0和m的位置用x来代替，可构造函数
要证明原不等式成立，只须证明f(0)真分数不等式的证明方法还有很多，请同学们课后再进行探索。
三、变换条件 创新问题
（1）若a>b>0,m>0，可以得到一个怎样的不等式？
分析：
和真分数不等式的已知条件相比，a和b恰好换位，
（2）若0分析：
三、变换条件 创新问题
根据真分数不等式
及其推论： 用不等号连结下列各式
由上述问题你可以得到一个更一般的结论吗？
分子、分母同加上一个相同的正数，则真分数越加越 （大或小），趋向于 ，假分数越加越 （大或小），趋向于 .
大
1
小
1
我们可以利用分数不等式这一性质，把一个分数的值放大或缩小，从而解决一类有关的不等式问题
四、实际运用 解决问题
例一、建筑学规定，民用住房的窗户面积必须小于地板面积。但按照采光标准，窗户面积与地板面积之比应不小于10%，并且越大，住宅采光条件越好。若同时增加相等的窗户面积和地板面积，住宅的采光条件是变好了还是变坏了？为什么？
答：变好了，根据真分数不等式可知。
四、实际运用 解决问题
根据真分数不等式性质有
分析：
由绝对值不等式性质有
四、实际运用 解决问题
例三、三角形ABC中，a、b、c是其三边，
求证
分析：
因为不等式右边是常数，为了便于求和，最好能把分母化为一致
四、实际运用 解决问题
例四、已知i,m,n N，且1求证：（1）niAmi(1+n)m.
分析：
∵1m i+1>0.
根据真分数不等式，有
由不等式性质有
四、实际运用 解决问题
例五、求证
分析：
根据假分数性质有
五、总结反思，深化认识
（1）真分数不等式：
推论（假分数的性质）
（2）某些分式型不等式的证明，可以运用真分数不等式及推论解决，关键是式中如何根据不等式的特征，选择恰当的正数m来分析解决问题。
（3）每年的高考试题都有一些题目是源于课本而高于课本的问题。
（4）引申创造（课后探究）（见资料）