鲁教版八年级上册分式复习课件
图片预览






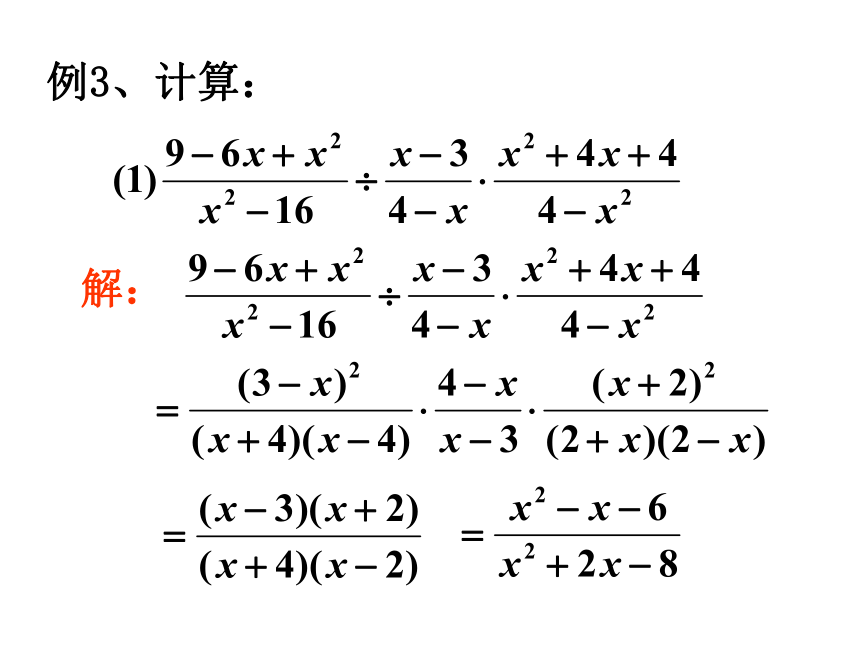
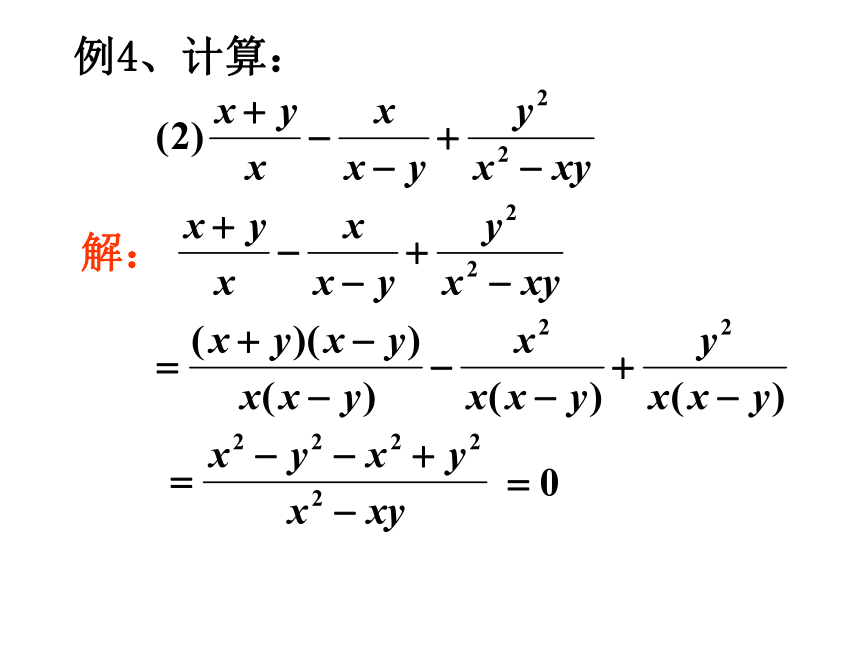

文档简介
(共27张PPT)
回顾与思考
分式
分式有意义
分式的值为零
分式约分
分式通分
分式方程
增根
概念
计算应用
分式的加、减、乘、除、乘方
解分式方程
——————————————
在分式有关的运算中,一般总是先把分子、分母分解因式;
注意:过程中,分子、分母一般保持分解因式的形式。
一、分式的意义:
解:由 m – 3 ≠0,得 m≠3。
所以当 m≠3 时,分式有意义;
由 m2 – 9 =0,得 m=±3。而当 m=3 时,
分母m – 3 =0,分式没有意义,故应舍去,
所以当 m= - 3时,分式的值为零。
例1:当 m 取何值时,分式
(1)有意义?
(2)值为零?
1.(1)X取何值时,分式 有义?
(2)x满足什么条件时,分式 无意义?
(3)x取何值时,分式 的值为零?
当分式的分母不等于零时,分式有意义;
当分式的分子等于零,而分母不等于零
时,分式的值为零。
例2、不改变分式的值,使 的分子、
分母的最高次项的系数为正整数。
解:
熟练地利用分式的基本性质,就系数、变符号即可。
例3、计算:
解:
例4、计算:
解:
例5.当 x = 200 时,求
的值.
解:
当 x = 200 时,原式=
3.计算
4.先化简,后求值:
1、 ,x=2008
2、
想一想:解分式方程一般需要几个步骤?
1.去分母.
2.解整式方程.
3.检验.
注意:不是所有的分式方程都有解
方程两边同乘以最简公分母,化分式方程为整式方程
把整式方程的根代入最简公分母,看结果是否为零,使最简公分母为零的根叫增根,舍去;使最简公分母不为零的根才是原方程的根.
例3 m为何值时,关于x的方程
会产生增根?
1.一项工程,需要在规定日期内完成,如果甲队独做,恰好如期完成,如果乙队独做,就要超过规定3天,现在由甲、乙两队合作2天,剩下的由乙队独做,也刚好在规定日期内完成,
问规定日期是几天?
列分式方程解应用题
2.一队学生去校外参观,他们出发30分钟时,学校要把一个紧急通知传给带队老师,派一名学生骑车从学校出发,按原路追赶队伍.若骑车的速度是队伍进行速度的2倍,这名学生追上队伍时离学校的距离是15千米,问这名学生从学校出发到追上队伍用了多少时间
3.把多边形的边数增加1 倍得到一个新多边形,原多边形内角和是新多边形内角和的0.4。
求原多边形的边数n应满足的方程。
n是多少?
例4、已知 ,求 的值。
剖析:通过已知,得出关系式 ,然后
利用 计算即可。
请你阅读下列计算过程,再回答所提出的问题:
题目计算
解:原式= (A)
= (B)
=x-3-3(x+1) (C)
=-2x-6 (D)
(1)上述计算过程中,从哪一步开始出现错误:_________
(2)从B到C是否正确,若不正确,错误的原因是______
(3)请你正确解答。
1、下列分式是最简分式的是
(A) (B) (C) (D)
2、若分式 有意义,则应满足的条件是
3、在代数式 、 、 、 中,分式共有
(A)1个 (B)2个 (C)3个 (D)4个
4、当x<0时,化简 的结果是 ( )
(A) – 2 (B) 0 (C)2 (D)无法确定
回顾与思考
分式
分式有意义
分式的值为零
分式约分
分式通分
分式方程
增根
概念
计算应用
分式的加、减、乘、除、乘方
解分式方程
——————————————
在分式有关的运算中,一般总是先把分子、分母分解因式;
注意:过程中,分子、分母一般保持分解因式的形式。
一、分式的意义:
解:由 m – 3 ≠0,得 m≠3。
所以当 m≠3 时,分式有意义;
由 m2 – 9 =0,得 m=±3。而当 m=3 时,
分母m – 3 =0,分式没有意义,故应舍去,
所以当 m= - 3时,分式的值为零。
例1:当 m 取何值时,分式
(1)有意义?
(2)值为零?
1.(1)X取何值时,分式 有义?
(2)x满足什么条件时,分式 无意义?
(3)x取何值时,分式 的值为零?
当分式的分母不等于零时,分式有意义;
当分式的分子等于零,而分母不等于零
时,分式的值为零。
例2、不改变分式的值,使 的分子、
分母的最高次项的系数为正整数。
解:
熟练地利用分式的基本性质,就系数、变符号即可。
例3、计算:
解:
例4、计算:
解:
例5.当 x = 200 时,求
的值.
解:
当 x = 200 时,原式=
3.计算
4.先化简,后求值:
1、 ,x=2008
2、
想一想:解分式方程一般需要几个步骤?
1.去分母.
2.解整式方程.
3.检验.
注意:不是所有的分式方程都有解
方程两边同乘以最简公分母,化分式方程为整式方程
把整式方程的根代入最简公分母,看结果是否为零,使最简公分母为零的根叫增根,舍去;使最简公分母不为零的根才是原方程的根.
例3 m为何值时,关于x的方程
会产生增根?
1.一项工程,需要在规定日期内完成,如果甲队独做,恰好如期完成,如果乙队独做,就要超过规定3天,现在由甲、乙两队合作2天,剩下的由乙队独做,也刚好在规定日期内完成,
问规定日期是几天?
列分式方程解应用题
2.一队学生去校外参观,他们出发30分钟时,学校要把一个紧急通知传给带队老师,派一名学生骑车从学校出发,按原路追赶队伍.若骑车的速度是队伍进行速度的2倍,这名学生追上队伍时离学校的距离是15千米,问这名学生从学校出发到追上队伍用了多少时间
3.把多边形的边数增加1 倍得到一个新多边形,原多边形内角和是新多边形内角和的0.4。
求原多边形的边数n应满足的方程。
n是多少?
例4、已知 ,求 的值。
剖析:通过已知,得出关系式 ,然后
利用 计算即可。
请你阅读下列计算过程,再回答所提出的问题:
题目计算
解:原式= (A)
= (B)
=x-3-3(x+1) (C)
=-2x-6 (D)
(1)上述计算过程中,从哪一步开始出现错误:_________
(2)从B到C是否正确,若不正确,错误的原因是______
(3)请你正确解答。
1、下列分式是最简分式的是
(A) (B) (C) (D)
2、若分式 有意义,则应满足的条件是
3、在代数式 、 、 、 中,分式共有
(A)1个 (B)2个 (C)3个 (D)4个
4、当x<0时,化简 的结果是 ( )
(A) – 2 (B) 0 (C)2 (D)无法确定
