6.3 三角形的中位线 一课一练(含解析)
文档属性
| 名称 | 6.3 三角形的中位线 一课一练(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-30 10:02:08 | ||
图片预览




文档简介
初中数学北师大版八年级下学期 第六章 6.3 三角形的中位线
一、单选题
1.如图,在△ABC中,点D、E、F分别是BC、AB、AC的中点,如果△ABC的周长为20,那么△DEF的周长是( ??)
A.?20?????????????????????????????????????????B.?15?????????????????????????????????????????C.?10?????????????????????????????????????????D.?5
2.如图,D、E分别是△ABC的边AB、AC的中点,若BC=6,则DE=(? )
A.?2???????????????????????????????????????????B.?3???????????????????????????????????????????C.?4???????????????????????????????????????????D.?5
3.Rt△ABC两直角边的长分别为6cm和8cm,则连接这两条直角边中点的线段长为(???? )
A.?10cm????????????????????????????????????B.?3cm????????????????????????????????????C.?4cm????????????????????????????????????D.?5cm
4.如图,现有一等腰直角三角形 的腰长为4, ,将 沿 折叠,使 的顶点恰好落在 边的中点 处,则线段 的长度为(? )
A.???????????????????????????????????????B.???????????????????????????????????????C.???????????????????????????????????????D.?
5.如图,M、N分别是△ABC的边AB、AC的中点,若∠A=65°,∠ANM=45°,则∠B=(?? )
A.?20°???????????????????????????????????????B.?45°???????????????????????????????????????C.?65°???????????????????????????????????????D.?70°
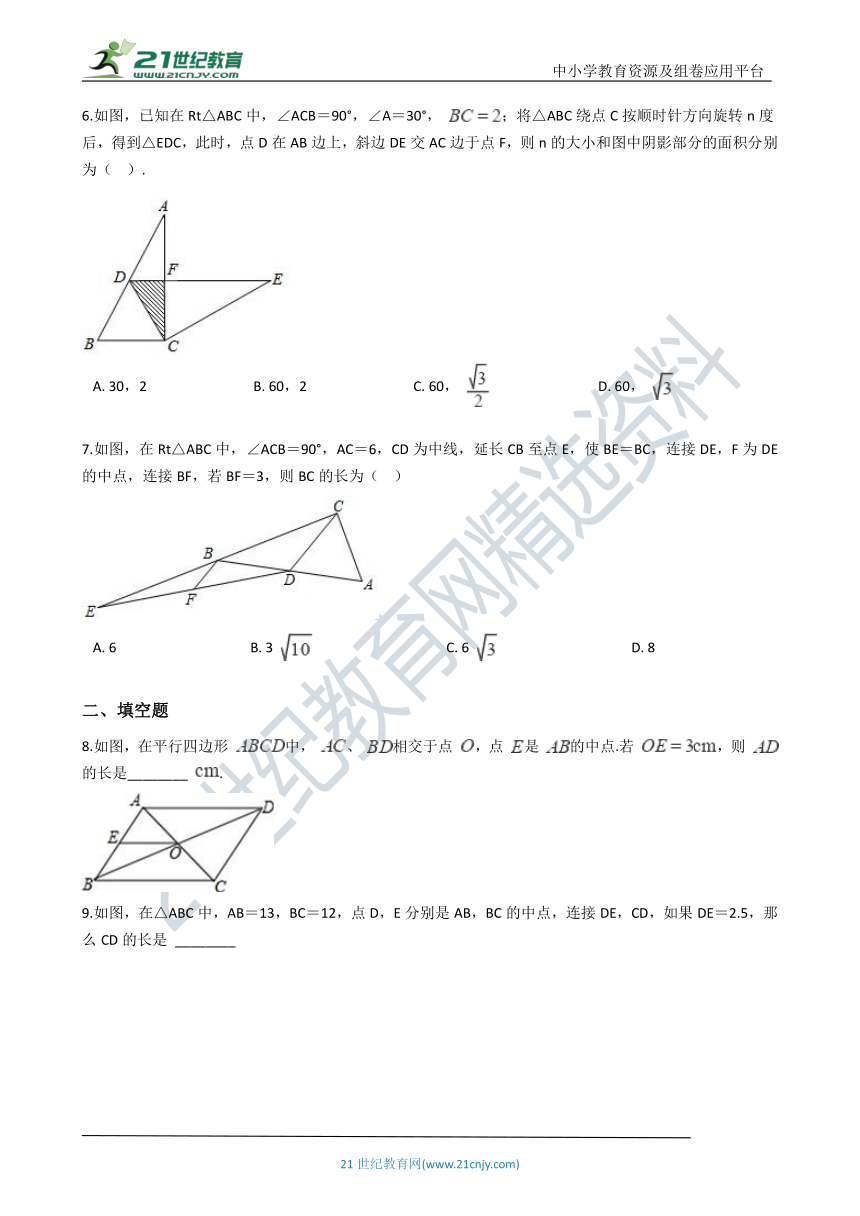
6.如图,已知在Rt△ABC中,∠ACB=90°,∠A=30°, ;将△ABC绕点C按顺时针方向旋转n度后,得到△EDC,此时,点D在AB边上,斜边DE交AC边于点F,则n的大小和图中阴影部分的面积分别为(?? ).
A.?30,2???????????????????????????????B.?60,2???????????????????????????????C.?60, ???????????????????????????????D.?60,
7.如图,在Rt△ABC中,∠ACB=90°,AC=6,CD为中线,延长CB至点E,使BE=BC,连接DE,F为DE的中点,连接BF,若BF=3,则BC的长为(?? )
A.?6???????????????????????????????????????B.?3 ???????????????????????????????????????C.?6 ???????????????????????????????????????D.?8
二、填空题
8.如图,在平行四边形 中, 、 相交于点 ,点 是 的中点.若 ,则 的长是________ .
9.如图,在△ABC中,AB=13,BC=12,点D,E分别是AB,BC的中点,连接DE,CD,如果DE=2.5,那么CD的长是 ________
10.如图,在 中, 分别是 的中点,连接 ,若 ,则四边形 的周长是________.
11.已知三角形的周长为20cm,连接各边中点所得的三角形的周长为________cm.
12.如图,任意四边形ABCD各边中点分别是E , F , G , H , 若对角线AC , BD的长都为10 cm , 则四边形EFGH的周长是________cm .
13.如图,?ABCD的对角线AC、BD相交于点O,OE∥AB交AD于点E,若OA=1,△AOE的周长等于5,则?ABCD的周长等于________.
14.如图,矩形ABCD中,对角线AC、BD相交于点O,点E、F分别是BO、BC的中点,若AB=5,BC=12,则EF=________;
15.如图,D、E分别是△ABC的边AB和AC的中点,若BC=18,则DE=________.
三、解答题
16.三角形三条边上的中线交于一点,这个点叫三角形的重心.如图G是 的重心.求证: .
17.如图,在四边形 中, ,接 ,E,F,M分别是 , , 的中点,连接 , .求证: .
18.如图,依次连接四边形 四边的中点 ,得到的新四边形 是什么四边形?请证明.
19.如图,△ABC中,D、E分别是边AB、AC的中点,点F是BC上一点,∠B=∠DEF.
(1)求证:四边形BDEF是平行四边形;
(2)直接写出当△ABC满足什么条件时,四边形BDEF是菱形.
答案解析部分
一、单选题
1.【答案】 C
解:∵D、E分别是△ABC的边BC、AB的中点,
∴DE= AC,同理 EF= BC,DF= AB,∴C△DEF=DE+EF+DF= (AC+BC+AB)= ×20=10.
故答案为:C.
2.【答案】 B
解:∵D、E分别是△ABC的边AB、AC的中点,
∴DE是△ABC的中位线,
∴DE= BC=3,
故答案为:B.
3.【答案】 D
解:∵Rt△ABC两直角边的长分别为6cm和8cm,
∴斜边= =10cm,
∴连接这两条直角边中点的线段长为 ×10=5cm.
故答案为:D.
4.【答案】 B
解:连接 ,交MN于点O,
∵等腰直角三角形 中, 的顶点恰好落在 边的中点 处,
∴ ⊥AB, ⊥MN, ,
∴AB∥MN,
∴AM=CM,CN=BN,
∴MN是三角形 的中位线,
∵等腰直角三角形 的腰长为4, ,
∴AB=4 ,
∴ =2 .
故答案为:B.
5.【答案】 D
解:∵ M、N分别是△ABC的边AB、AC的中点,
∴MN∥BC,
∴∠C=∠ANM=45°,
∴∠B=180°-∠A-∠C=180°-65°-45°=70°,
故答案为:D.
6.【答案】 C
解:∵∠ACB=90°,∠A=30°
∴ ,
∴
∵将△ABC绕点C按顺时针方向旋转n度后,得到△EDC,
∴ ,
∴
∴
∴ ,
∴ ,即
∴
∴
∴
∴
∴阴影部分的面积
∵
∴阴影部分的面积
故答案为:C.
7.【答案】 C
解: F为DE的中点,
∠ACB=90°,CD为中线,
故答案为:C.
二、填空题
8.【答案】 6
解:∵四边形ABCD是平行四边形
∴ 点O是BD的中点
∵点E是AB的中点
∴
故答案为:6.
9.【答案】 6.5
解:∵D,E分别是AB,BC的中点,
∴AC=2DE=5,AC∥DE,
AC2+BC2=52+122=169,
AB2=132=169,
∴AC2+BC2=AB2 ,
∴∠ACB=90°,
∵AC∥DE,
∴∠DEB=90°
, 又∵E是BC的中点,
∴直线DE是线段BC的垂直平分线,
∴DC=BD= AB=6.5,
故答案是:6.5.
10.【答案】 22cm
解:∵ 分别是 的中点, ,
∴ , ,
, ,
∴四边形 的周长为 ,
故答案为: .
11.【答案】 10
解:如图,
∵ 分别为 的中点,
∴ ,
∵ ,
∴ ,
故答案为:10.
12.【答案】 20
解:∵E、F、G、H分别为AB、BC、CD、AD边的中点,
∴EF为△ABC的中位线,HG为△ACD的中位线,EH为△ABD的中位线,FG为△BCD的中位线,
∴EH=BD=5cm,FG=BD=5cm,EF=AC=5cm,HG=AC=5cm,
∴四边形EFGH的周长=EH+HG+FG+EF=5+5+5+5=20cm.
故答案为20.
13.【答案】 16
解:∵四边形ABCD是平行四边形,
∴AB=CD,AD=BC,OB=OD,
∵OE∥AB,
∴AE=ED,
∴OE是△ABD的中位线,
∴AB=2OE,AD=2AE;
∵△AOE的周长等于5,OA=1,
∴OA+AE+OE=5,
∴AE+OE=5?OA=5?1=4,
∴AB+AD=2(AE+OE)=2×4=8,
∴?ABCD的周长=2×(AB+AD)=2×8=16.
故答案为:16.
14.【答案】
解:∵四边形ABCD是矩形,
∴∠BAD=90°,OC= AC,AD=BC=12,
∴AC= =13,
∴OC= ,
∵点E、F分别是BO、BC的中点,
∴EF是△BOC的中位线,
∴EF= OC= ,
故答案为: .
15.【答案】 9
解:∵D,E分别是△ABC的边AB,AC的中点,
∴DE是△ABC的中位线,BC=18,
∴DE= BC=9,
故答案为:9.
三、解答题
16.【答案】 证明:过点D作DH∥AB,交CE于点H,
∵AD是△ABC的中线,
∴点D是BC的中点,
∴DH是△BCE的中位线,
∴BE=2DH,DH∥AB,
∵CE是△BCE的中线,
∴AE=BE,
∴AE=2DH,
∵DH∥AB,
∴△AEG∽△DHG,
∴ ,
∴AG=2GD,
即AD=3GD.
17.【答案】 证明: ,F分别是 , 的中点,
是 的中位线,
.
, 是 的中点,
.
18.【答案】 解:四边形EFGH是平行四边形,理由如下:
连接BD
∵E,H分别是AB,AD的中点
∴EH∥BD,EH=
同理FG∥BD,FG=
∴EH∥FG且EH=FG
∴四边形EFGH是平行四边形
19.【答案】 (1)证明:∵? 点D、E分别是边AB、AC的中点,
∴? DE是△ABC的中位线.
∴? DE∥BC.
∴? ∠B=∠ADE.
又? ∠B=∠DEF.
∴? ∠ADE=∠DEF.
∴? BD∥EF.
∵? DE∥BC,BD∥EF,
∴? 四边形BDEF是平行四边形.
(2)证明:答案不唯一,如AB=BC.
∵ DE是△ABC的中位线
∴BD= AB ,BF= ?BC
∵ AB=BC
∴BD=BF
∴ BDEF是菱形
一、单选题
1.如图,在△ABC中,点D、E、F分别是BC、AB、AC的中点,如果△ABC的周长为20,那么△DEF的周长是( ??)
A.?20?????????????????????????????????????????B.?15?????????????????????????????????????????C.?10?????????????????????????????????????????D.?5
2.如图,D、E分别是△ABC的边AB、AC的中点,若BC=6,则DE=(? )
A.?2???????????????????????????????????????????B.?3???????????????????????????????????????????C.?4???????????????????????????????????????????D.?5
3.Rt△ABC两直角边的长分别为6cm和8cm,则连接这两条直角边中点的线段长为(???? )
A.?10cm????????????????????????????????????B.?3cm????????????????????????????????????C.?4cm????????????????????????????????????D.?5cm
4.如图,现有一等腰直角三角形 的腰长为4, ,将 沿 折叠,使 的顶点恰好落在 边的中点 处,则线段 的长度为(? )
A.???????????????????????????????????????B.???????????????????????????????????????C.???????????????????????????????????????D.?
5.如图,M、N分别是△ABC的边AB、AC的中点,若∠A=65°,∠ANM=45°,则∠B=(?? )
A.?20°???????????????????????????????????????B.?45°???????????????????????????????????????C.?65°???????????????????????????????????????D.?70°
6.如图,已知在Rt△ABC中,∠ACB=90°,∠A=30°, ;将△ABC绕点C按顺时针方向旋转n度后,得到△EDC,此时,点D在AB边上,斜边DE交AC边于点F,则n的大小和图中阴影部分的面积分别为(?? ).
A.?30,2???????????????????????????????B.?60,2???????????????????????????????C.?60, ???????????????????????????????D.?60,
7.如图,在Rt△ABC中,∠ACB=90°,AC=6,CD为中线,延长CB至点E,使BE=BC,连接DE,F为DE的中点,连接BF,若BF=3,则BC的长为(?? )
A.?6???????????????????????????????????????B.?3 ???????????????????????????????????????C.?6 ???????????????????????????????????????D.?8
二、填空题
8.如图,在平行四边形 中, 、 相交于点 ,点 是 的中点.若 ,则 的长是________ .
9.如图,在△ABC中,AB=13,BC=12,点D,E分别是AB,BC的中点,连接DE,CD,如果DE=2.5,那么CD的长是 ________
10.如图,在 中, 分别是 的中点,连接 ,若 ,则四边形 的周长是________.
11.已知三角形的周长为20cm,连接各边中点所得的三角形的周长为________cm.
12.如图,任意四边形ABCD各边中点分别是E , F , G , H , 若对角线AC , BD的长都为10 cm , 则四边形EFGH的周长是________cm .
13.如图,?ABCD的对角线AC、BD相交于点O,OE∥AB交AD于点E,若OA=1,△AOE的周长等于5,则?ABCD的周长等于________.
14.如图,矩形ABCD中,对角线AC、BD相交于点O,点E、F分别是BO、BC的中点,若AB=5,BC=12,则EF=________;
15.如图,D、E分别是△ABC的边AB和AC的中点,若BC=18,则DE=________.
三、解答题
16.三角形三条边上的中线交于一点,这个点叫三角形的重心.如图G是 的重心.求证: .
17.如图,在四边形 中, ,接 ,E,F,M分别是 , , 的中点,连接 , .求证: .
18.如图,依次连接四边形 四边的中点 ,得到的新四边形 是什么四边形?请证明.
19.如图,△ABC中,D、E分别是边AB、AC的中点,点F是BC上一点,∠B=∠DEF.
(1)求证:四边形BDEF是平行四边形;
(2)直接写出当△ABC满足什么条件时,四边形BDEF是菱形.
答案解析部分
一、单选题
1.【答案】 C
解:∵D、E分别是△ABC的边BC、AB的中点,
∴DE= AC,同理 EF= BC,DF= AB,∴C△DEF=DE+EF+DF= (AC+BC+AB)= ×20=10.
故答案为:C.
2.【答案】 B
解:∵D、E分别是△ABC的边AB、AC的中点,
∴DE是△ABC的中位线,
∴DE= BC=3,
故答案为:B.
3.【答案】 D
解:∵Rt△ABC两直角边的长分别为6cm和8cm,
∴斜边= =10cm,
∴连接这两条直角边中点的线段长为 ×10=5cm.
故答案为:D.
4.【答案】 B
解:连接 ,交MN于点O,
∵等腰直角三角形 中, 的顶点恰好落在 边的中点 处,
∴ ⊥AB, ⊥MN, ,
∴AB∥MN,
∴AM=CM,CN=BN,
∴MN是三角形 的中位线,
∵等腰直角三角形 的腰长为4, ,
∴AB=4 ,
∴ =2 .
故答案为:B.
5.【答案】 D
解:∵ M、N分别是△ABC的边AB、AC的中点,
∴MN∥BC,
∴∠C=∠ANM=45°,
∴∠B=180°-∠A-∠C=180°-65°-45°=70°,
故答案为:D.
6.【答案】 C
解:∵∠ACB=90°,∠A=30°
∴ ,
∴
∵将△ABC绕点C按顺时针方向旋转n度后,得到△EDC,
∴ ,
∴
∴
∴ ,
∴ ,即
∴
∴
∴
∴
∴阴影部分的面积
∵
∴阴影部分的面积
故答案为:C.
7.【答案】 C
解: F为DE的中点,
∠ACB=90°,CD为中线,
故答案为:C.
二、填空题
8.【答案】 6
解:∵四边形ABCD是平行四边形
∴ 点O是BD的中点
∵点E是AB的中点
∴
故答案为:6.
9.【答案】 6.5
解:∵D,E分别是AB,BC的中点,
∴AC=2DE=5,AC∥DE,
AC2+BC2=52+122=169,
AB2=132=169,
∴AC2+BC2=AB2 ,
∴∠ACB=90°,
∵AC∥DE,
∴∠DEB=90°
, 又∵E是BC的中点,
∴直线DE是线段BC的垂直平分线,
∴DC=BD= AB=6.5,
故答案是:6.5.
10.【答案】 22cm
解:∵ 分别是 的中点, ,
∴ , ,
, ,
∴四边形 的周长为 ,
故答案为: .
11.【答案】 10
解:如图,
∵ 分别为 的中点,
∴ ,
∵ ,
∴ ,
故答案为:10.
12.【答案】 20
解:∵E、F、G、H分别为AB、BC、CD、AD边的中点,
∴EF为△ABC的中位线,HG为△ACD的中位线,EH为△ABD的中位线,FG为△BCD的中位线,
∴EH=BD=5cm,FG=BD=5cm,EF=AC=5cm,HG=AC=5cm,
∴四边形EFGH的周长=EH+HG+FG+EF=5+5+5+5=20cm.
故答案为20.
13.【答案】 16
解:∵四边形ABCD是平行四边形,
∴AB=CD,AD=BC,OB=OD,
∵OE∥AB,
∴AE=ED,
∴OE是△ABD的中位线,
∴AB=2OE,AD=2AE;
∵△AOE的周长等于5,OA=1,
∴OA+AE+OE=5,
∴AE+OE=5?OA=5?1=4,
∴AB+AD=2(AE+OE)=2×4=8,
∴?ABCD的周长=2×(AB+AD)=2×8=16.
故答案为:16.
14.【答案】
解:∵四边形ABCD是矩形,
∴∠BAD=90°,OC= AC,AD=BC=12,
∴AC= =13,
∴OC= ,
∵点E、F分别是BO、BC的中点,
∴EF是△BOC的中位线,
∴EF= OC= ,
故答案为: .
15.【答案】 9
解:∵D,E分别是△ABC的边AB,AC的中点,
∴DE是△ABC的中位线,BC=18,
∴DE= BC=9,
故答案为:9.
三、解答题
16.【答案】 证明:过点D作DH∥AB,交CE于点H,
∵AD是△ABC的中线,
∴点D是BC的中点,
∴DH是△BCE的中位线,
∴BE=2DH,DH∥AB,
∵CE是△BCE的中线,
∴AE=BE,
∴AE=2DH,
∵DH∥AB,
∴△AEG∽△DHG,
∴ ,
∴AG=2GD,
即AD=3GD.
17.【答案】 证明: ,F分别是 , 的中点,
是 的中位线,
.
, 是 的中点,
.
18.【答案】 解:四边形EFGH是平行四边形,理由如下:
连接BD
∵E,H分别是AB,AD的中点
∴EH∥BD,EH=
同理FG∥BD,FG=
∴EH∥FG且EH=FG
∴四边形EFGH是平行四边形
19.【答案】 (1)证明:∵? 点D、E分别是边AB、AC的中点,
∴? DE是△ABC的中位线.
∴? DE∥BC.
∴? ∠B=∠ADE.
又? ∠B=∠DEF.
∴? ∠ADE=∠DEF.
∴? BD∥EF.
∵? DE∥BC,BD∥EF,
∴? 四边形BDEF是平行四边形.
(2)证明:答案不唯一,如AB=BC.
∵ DE是△ABC的中位线
∴BD= AB ,BF= ?BC
∵ AB=BC
∴BD=BF
∴ BDEF是菱形
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
