9.3角的度量

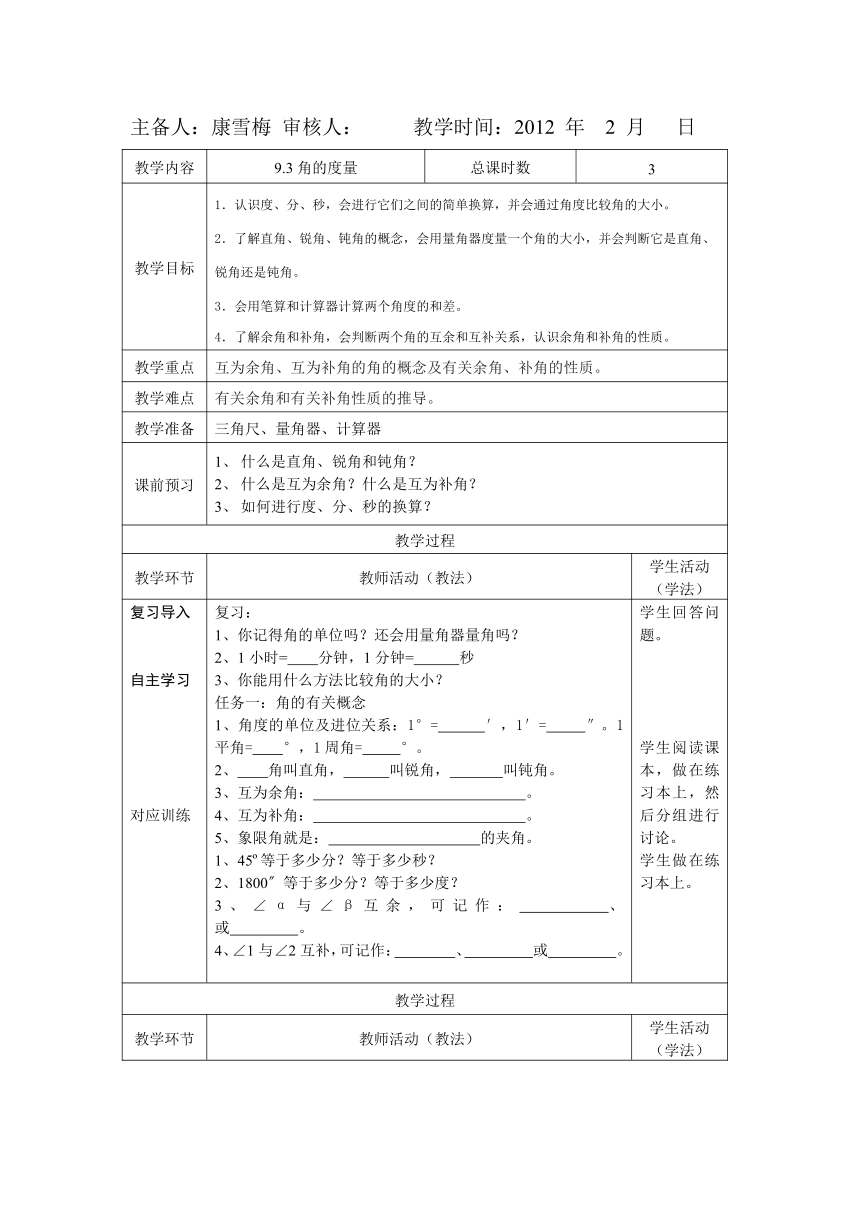
主备人：康雪梅 审核人： 教学时间：2012 年 2 月 日
教学内容 9.3角的度量 总课时数 3
教学目标 1．认识度、分、秒，会进行它们之间的简单换算，并会通过角度比较角的大小。2．了解直角、锐角、钝角的概念，会用量角器度量一个角的大小，并会判断它是直角、锐角还是钝角。3．会用笔算和计算器计算两个角度的和差。4．了解余角和补角，会判断两个角的互余和互补关系，认识余角和补角的性质。
教学重点 互为余角、互为补角的角的概念及有关余角、补角的性质。
教学难点 有关余角和有关补角性质的推导。
教学准备 三角尺、量角器、计算器
课前预习 什么是直角、锐角和钝角？什么是互为余角？什么是互为补角？如何进行度、分、秒的换算？
教学过程
教学环节 教师活动（教法） 学生活动（学法）
复习导入自主学习对应训练 复习：1、你记得角的单位吗？还会用量角器量角吗？ 2、1小时= 分钟，1分钟= 秒3、你能用什么方法比较角的大小？ 任务一：角的有关概念1、角度的单位及进位关系：1°= ′，1′= ″。1平角= °，1周角= °。2、 角叫直角， 叫锐角， 叫钝角。3、互为余角： 。4、互为补角： 。5、象限角就是： 的夹角。1、45 等于多少分？等于多少秒？2、1800〞等于多少分？等于多少度？3、∠α与∠β互余，可记作：　　　　、 或 。4、∠1与∠2互补，可记作：　　　　、 或 。 学生回答问题。学生阅读课本，做在练习本上，然后分组进行讨论。学生做在练习本上。
教学过程
教学环节 教师活动（教法） 学生活动（学法）
精讲点拨系列训练 任务二：比较角的大小1、用量角器分别量出图1中的∠DOA，∠DOB，∠DOC，∠DOE，比较它们的大小并指出其中的锐角、直角、钝角和平角。1、53.37 =___ ___′____〞; 24 12′36〞=______ 90 -35 27′=___ ___′。2、已知∠α=37°50′，∠β=52°10′，求∠α+∠β与∠β+∠α。3、一个角的余角是它的，求这个角的度数。总结:同角或等角的余角相等。 同角或等角的补角相等。1、0.75°= ′ ″ 3600″= ′= °2、求220，，30 12′36〞的余角和补角3、∠1=300，∠2的补角是1200，则∠1，∠2有什么关系？4、已知，如图所示长方形CBHG中，CD，GF是∠A的两边上的一部分。(1)画出∠A，并量出∠A的度数；(2)分别量∠1，∠2，∠3与∠4的度数；(3)说出∠1与∠2，∠3与∠4之间是什么关系？你能说出∠1，∠3，∠A的和与平角之间的关系吗？5.小亮和小颖分别从A，B两点观测旗杆C，得到的象限角分别为北偏东30°和北偏西60°，你能用三角板画出旗杆C的位置吗？ 学生运用量角器进行测量，然后进行比较。学生讨论：同角或等角的补角或余角有什么关系？学生做在练习本上。
教学过程
教学环节 教师活动（教法） 学生活动（学法）
当堂达标小结： 作业： 1、已知∠α=35o，则∠α的余角的度数是（ ）A、55o B、45o C、145o D、135o2、下列等式中不正确的是（ ）A、1直角=90o B、1周角=2平角 C、1平角=180o D、1平角=4直角3、36.33o可化为（ ）A、36o30′33″ B、36o33′ C、36o30′30″ D、36o19′48″4、如果∠1与∠2互余，∠2与∠3互余，则∠1与∠3的关系是（ ）A、∠1>∠3 B、∠1=∠3 C、∠1<∠3 D、不能确定5、72o20′的角的余角等于 ；25o31′的角的补角等于 。6、已知∠A与∠B互余，若∠A=70o，则∠B的度数为 。7、∠α与∠β互余，∠α是∠β的2倍，则∠β= 。8、一个角的补角是这个角的余角的3倍，则这个角为 度。今天你有什么收获？习题9.3A组第2、3题。 学生做在练习本上。
课后反思 总体来说这节课上的比较成功。学生们能够熟练地进行角的度数之间的转化，能进行锐角、直角和钝角之间的区分。但是在学习余角和补角时出现了相混淆的现象，在以后的讲课中一定要加强这方面的练习。学生更习惯用计算器进行计算，虽然说，他们这个年龄段很容易接受新事物，但是有的学生却养成了是数都要用计算器的习惯，这不是一个好习惯。在以后的学习中应该让学生更多的用笔算，用心算。