北师大版高中数学(必修1)2.5《简单的幂函数》ppt课件
文档属性
| 名称 | 北师大版高中数学(必修1)2.5《简单的幂函数》ppt课件 |  | |
| 格式 | zip | ||
| 文件大小 | 85.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-03-30 17:14:21 | ||
图片预览





文档简介
(共13张PPT)
我们先来看看几个具体的问题:
(1)如果张红买了每千克1元的蔬菜x千克,所需的钱数为y元,那么她需要支付_____________
y=x (元)
(2)如果正方形的边长为 x,面积为y,那么正方形的面
积__________
(3)如果正方体的边长为x,体积为y,那么正方体的体积______
(4)如果某人 x s内骑车行进1 km,那么他骑车的平均
速度 ______________
y=x2
y=x3
y=x-1 (km/s)
思考:这些函数有什么共同的特
征?
共同特征:函数解析式是幂的形式,且指数是常数,底数是自变量.
情景引入,提出问题:
一、幂函数概念
一般地,如果一个函数,底数是自变量x,指数是常量 a ,即 y=xa ,这样的函数叫做幂函数.
如:y=x, y=x2,y=x5,y=x-1, y=x-4等都是幂函数.
注意:幂函数中的指数 a可以为任意实数.在中学阶段我们只关注a=1,2,3,-1,1/2
学生活动1 归纳幂函数的概念
一、幂函数概念
(1)判断下列函数是否为幂函数.
(1) y=x4
(3) y= -x2
(5) y=x-5
(6) y=(2x)3
学生活动2 理解应用
(2) 幂函数y=f(x)的图像过点(2,8),求函数的解析式.
答案:y=x3
一、幂函数概念
学生活动3 归纳幂函数的特征:
1. y=xa的系数是1;其特征可归纳为“两个1”,即:系数为1,只有1项。
2. 底数为x而不是x的代数式,如2x或x-2等;
3. 幂函数y=xa中指数a确定则幂函数确定。故用
待定系数法就解析式只需一个条件,如已知图像上的一个点的
坐标等。
一、幂函数概念
二、幂函数的图象
1
1
0
x
y
2
8
-1
-1
-2
-8
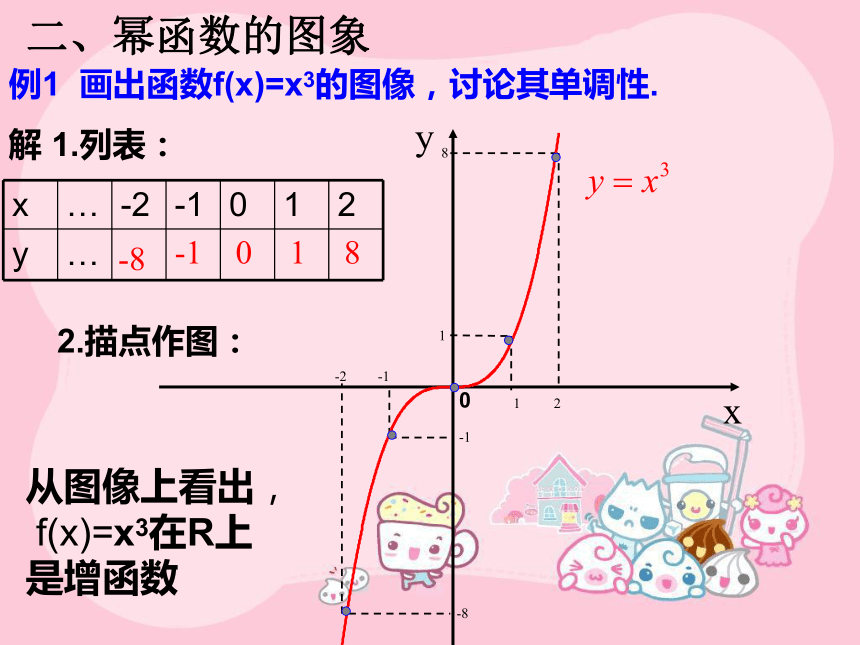
例1 画出函数f(x)=x3的图像,讨论其单调性.
-8
x … -2 -1 0 1 2
y …
1
-1
0
8
从图像上看出,
f(x)=x3在R上
是增函数
解 1.列表:
2.描点作图:
思考:函数图象上横坐标互为相反数的点的纵坐标有什么关系?
-x
f(-x)
x
f(x)
x
y
o
A‘(-x,-y)
A(x,y)
学生活动4 由图像得出奇偶函数的概念
奇函数定义:
一般地,图像关于原点
对称的函数叫作奇函数
在奇函数中,f(-x)和 f(x)的绝对值相等,符号相反,即
f(-x)= - f(x)
结论:函数f(x)=x3 的图像关于原点对称。
(1)观察f(x)=x3的图象
偶函数定义:
一般地,图像关于y轴对称的函数叫作偶函数.
x
y
o
-x
x
f(-x)
A( x,y)
A’(-x,y)
f(x)
f(x)=x2
思考:函数图象上横坐标互为相反数的点的纵坐标有什么关系?
f(-x)= f(x)
(2)观察函数f(x)=x2图像
在偶函数中, f(-x)和f(x)的值
相等,即
结论:函数f(x)=x2 的图像关于y轴对称。
[-b,-a]
[a ,b]
☆对奇函数、偶函数定义的说明:
(1) 函数具有奇偶性的前提是:定义域关于原点对称。
o
x
(2) 若f(x)为奇函数, 则f(-x)=-f(x)成立,反之亦然。
若f(x)为偶函数, 则f(-x)= f(x) 成立,反之亦然。
(3) 当函数f(x)是奇函数或偶函数时,称函数具有奇偶性。
例2 判断f(x)=-2x5和g(x)=x4+2的奇偶性.
用定义证明函数奇偶性的步骤:
1. 检验定义域是否关于原点对称 ;
2. 求f(-x),化简,整理;
3. 比较f(x)与 f(-x),如果第二步不易化简 ,
可直接计算f(x) + f(-x)
另:判断函数奇偶性的还可用图象法,或借用一些熟知的基本函数的奇偶性.
(4)练习:判断下列函数奇偶性
奇函数
非奇非偶函数
X(1-x),(x<0)
X(1-x),(x>0)
{
奇函数
三、课堂小结
(1) 幂函数的概念;
(2) 函数奇偶性的概念及证明.
作业:课本50页A组 2题 ,3题(2)(4)
我们先来看看几个具体的问题:
(1)如果张红买了每千克1元的蔬菜x千克,所需的钱数为y元,那么她需要支付_____________
y=x (元)
(2)如果正方形的边长为 x,面积为y,那么正方形的面
积__________
(3)如果正方体的边长为x,体积为y,那么正方体的体积______
(4)如果某人 x s内骑车行进1 km,那么他骑车的平均
速度 ______________
y=x2
y=x3
y=x-1 (km/s)
思考:这些函数有什么共同的特
征?
共同特征:函数解析式是幂的形式,且指数是常数,底数是自变量.
情景引入,提出问题:
一、幂函数概念
一般地,如果一个函数,底数是自变量x,指数是常量 a ,即 y=xa ,这样的函数叫做幂函数.
如:y=x, y=x2,y=x5,y=x-1, y=x-4等都是幂函数.
注意:幂函数中的指数 a可以为任意实数.在中学阶段我们只关注a=1,2,3,-1,1/2
学生活动1 归纳幂函数的概念
一、幂函数概念
(1)判断下列函数是否为幂函数.
(1) y=x4
(3) y= -x2
(5) y=x-5
(6) y=(2x)3
学生活动2 理解应用
(2) 幂函数y=f(x)的图像过点(2,8),求函数的解析式.
答案:y=x3
一、幂函数概念
学生活动3 归纳幂函数的特征:
1. y=xa的系数是1;其特征可归纳为“两个1”,即:系数为1,只有1项。
2. 底数为x而不是x的代数式,如2x或x-2等;
3. 幂函数y=xa中指数a确定则幂函数确定。故用
待定系数法就解析式只需一个条件,如已知图像上的一个点的
坐标等。
一、幂函数概念
二、幂函数的图象
1
1
0
x
y
2
8
-1
-1
-2
-8
例1 画出函数f(x)=x3的图像,讨论其单调性.
-8
x … -2 -1 0 1 2
y …
1
-1
0
8
从图像上看出,
f(x)=x3在R上
是增函数
解 1.列表:
2.描点作图:
思考:函数图象上横坐标互为相反数的点的纵坐标有什么关系?
-x
f(-x)
x
f(x)
x
y
o
A‘(-x,-y)
A(x,y)
学生活动4 由图像得出奇偶函数的概念
奇函数定义:
一般地,图像关于原点
对称的函数叫作奇函数
在奇函数中,f(-x)和 f(x)的绝对值相等,符号相反,即
f(-x)= - f(x)
结论:函数f(x)=x3 的图像关于原点对称。
(1)观察f(x)=x3的图象
偶函数定义:
一般地,图像关于y轴对称的函数叫作偶函数.
x
y
o
-x
x
f(-x)
A( x,y)
A’(-x,y)
f(x)
f(x)=x2
思考:函数图象上横坐标互为相反数的点的纵坐标有什么关系?
f(-x)= f(x)
(2)观察函数f(x)=x2图像
在偶函数中, f(-x)和f(x)的值
相等,即
结论:函数f(x)=x2 的图像关于y轴对称。
[-b,-a]
[a ,b]
☆对奇函数、偶函数定义的说明:
(1) 函数具有奇偶性的前提是:定义域关于原点对称。
o
x
(2) 若f(x)为奇函数, 则f(-x)=-f(x)成立,反之亦然。
若f(x)为偶函数, 则f(-x)= f(x) 成立,反之亦然。
(3) 当函数f(x)是奇函数或偶函数时,称函数具有奇偶性。
例2 判断f(x)=-2x5和g(x)=x4+2的奇偶性.
用定义证明函数奇偶性的步骤:
1. 检验定义域是否关于原点对称 ;
2. 求f(-x),化简,整理;
3. 比较f(x)与 f(-x),如果第二步不易化简 ,
可直接计算f(x) + f(-x)
另:判断函数奇偶性的还可用图象法,或借用一些熟知的基本函数的奇偶性.
(4)练习:判断下列函数奇偶性
奇函数
非奇非偶函数
X(1-x),(x<0)
X(1-x),(x>0)
{
奇函数
三、课堂小结
(1) 幂函数的概念;
(2) 函数奇偶性的概念及证明.
作业:课本50页A组 2题 ,3题(2)(4)
