19.2.2一次函数与实际问题-2020-2021学年人教版八年级数学下册导学案(Word版含详解)
文档属性
| 名称 | 19.2.2一次函数与实际问题-2020-2021学年人教版八年级数学下册导学案(Word版含详解) |

|
|
| 格式 | doc | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-31 10:54:08 | ||
图片预览



文档简介
19.2.2 一次函数
第4课时 一次函数与实际问题
学习目标:
1.巩固一次函数知识,灵活运用变量关系解决相关的实际问题.
2.有机地把各种数学模型通过函数统一起来,提高解决实际问题的能力.
3.认识数学在现实生活中的意义,提高运用数学知识解决实际问题的能力.
学习重点:学会用一次函数解决实际问题.
一、课前检测
已知直线经过点(9,0)和点(24,20),求这条直线的函数解析式.
二、温故知新
1.一次函数的解析式的一般形式为 .
2.画函数图象的一般步骤是 、 、 .
3.说一说用待定系数法求一次函数解析式的步骤.
三、预习导航(预习教材第94-95页,标出你认为重要的关键词)
1.已知
(1)分别求出当x=1,x=5时y的值;
(2)y是x的函数吗?它与一次函数有何区别?
(3)若y是x的函数,你能画出它的函数图象吗?
2.自主归纳:
与上题中形式相同的函数叫做分段函数.
注意:(1)它是一个函数,不要误以为是两个函数;
(2)对于不同取值范围的自变量,它所对应的函数解析式不同;
(3)它的函数图象也是由两部分组成.
四、自学自测
某市出租车计费标准为:起步价8元(3千米及以内),超过3千米的部分按每千米2.6元计算,设行驶的路程为x千米,应交的车费为y元.
(1)若小明乘出租车行驶了2千米,应收费______元;
若行驶5千米,应收费______元;
(2)请写出当 0<x≤3和x>3时y与x之间的函数解析式;
(3)若某顾客走了30千米,你能算出他应付多少元钱吗?
五、我的疑惑(反思)
__________________________________________________________________________________________________________________________________________________
要点探究
探究点1:一次函数与实际问题
问题1 温度的度量有两种:摄氏温度和华氏温度.
水的沸点温度是100℃,用华氏温度度量为212℉;水的冰点温度是0℃,用华氏温度度量为32 ℉.已知摄氏温度与华氏温度的关系近似地为一次函数关系,你能不能想出一个办法方便地把华氏温度换算成摄氏温度?
方法总结:已知两个变量是一次函数关系,直接设其解析式,然后根据题目两个已知条件,用待定系数法求解即可.
二、精讲点拨
例1 为节约用水,某市制定以下用水收费标准,每户每月用水不超过8立方米,每立方米收取1元外加0.3元的污水处理费;超过8立方米时,超过部分每立方米收取1.5元外加1.2元污水处理费,现设一户每月用水x立方米,应缴水费y元.
(1)求出y关于x的函数解析式;
(2)该市一户某月若用水10立方米时,求应缴水费多少元?
(3)该市一户某月缴水费26.6元,求该户这月用水量.
方法总结:不同取值范围的自变量所对应的函数解析式不同是分段函数.利用分段函数解决实际问题时,注意自变量要与解析式对应.
三、变式训练
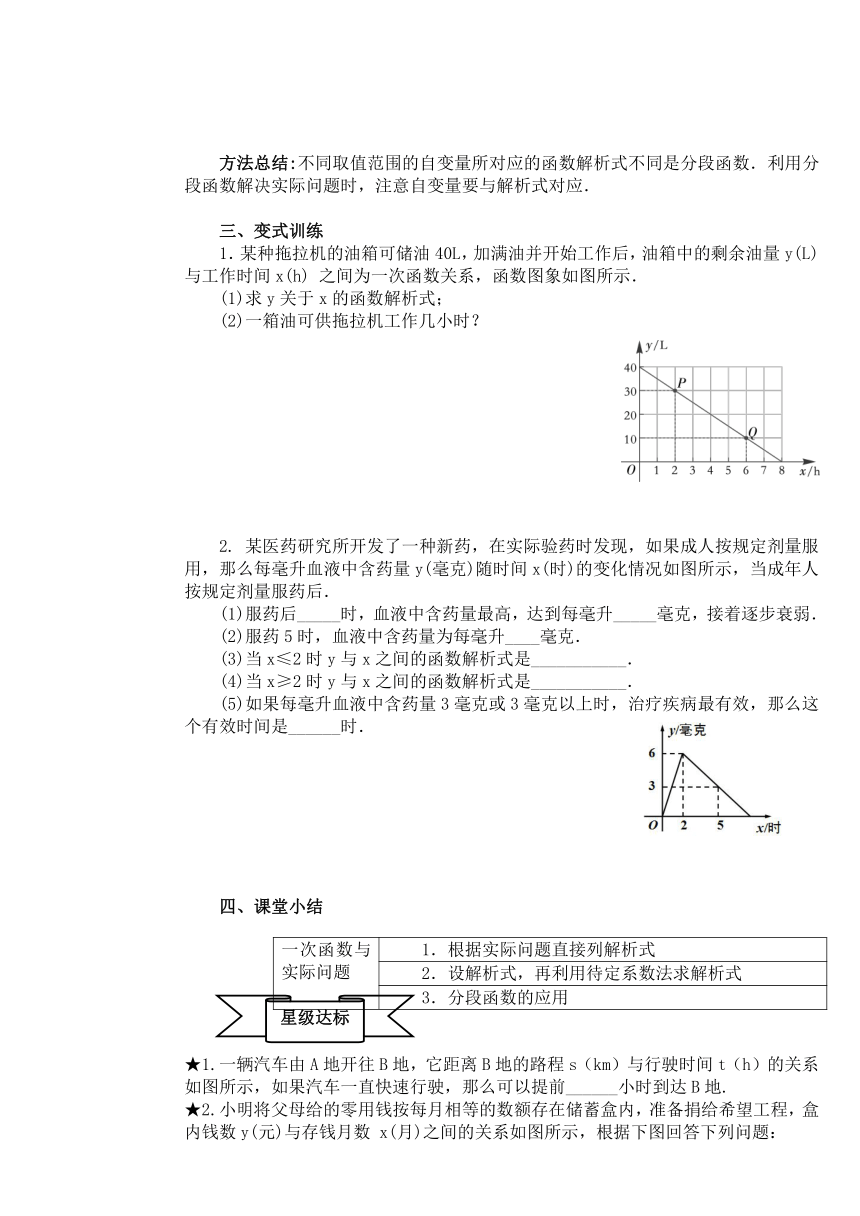
1.某种拖拉机的油箱可储油40L,加满油并开始工作后,油箱中的剩余油量y(L)与工作时间x(h) 之间为一次函数关系,函数图象如图所示.
(1)求y关于x的函数解析式;
(2)一箱油可供拖拉机工作几小时?
2. 某医药研究所开发了一种新药,在实际验药时发现,如果成人按规定剂量服用,那么每毫升血液中含药量y(毫克)随时间x(时)的变化情况如图所示,当成年人按规定剂量服药后.
(1)服药后_____时,血液中含药量最高,达到每毫升_____毫克,接着逐步衰弱.
(2)服药5时,血液中含药量为每毫升____毫克.
(3)当x≤2时y与x之间的函数解析式是___________.
(4)当x≥2时y与x之间的函数解析式是___________.
(5)如果每毫升血液中含药量3毫克或3毫克以上时,治疗疾病最有效,那么这个有效时间是______时.
四、课堂小结
一次函数与实际问题 1.根据实际问题直接列解析式
2.设解析式,再利用待定系数法求解析式
3.分段函数的应用
★1.一辆汽车由A地开往B地,它距离B地的路程s(km)与行驶时间t(h)的关系如图所示,如果汽车一直快速行驶,那么可以提前______小时到达B地.
★2.小明将父母给的零用钱按每月相等的数额存在储蓄盒内,准备捐给希望工程,盒内钱数y(元)与存钱月数 x(月)之间的关系如图所示,根据下图回答下列问题:
求出y关于x的函数解析式.
根据关系式计算,小明经过几个月才能存够200元?
★★3.一个试验室在0:00—2:00保持20℃的恒温,在2:00—4:00匀速升温,每小时升高5℃.写出试验室温度T(单位:℃)关于时间t(单位:h)的函数解析式,并画出函数图象.
★★★4.近几年来,由于经济和社会发展迅速,用电量越来越多.为缓解用电紧张,某电力公司特制定了新的用电收费标准,每月用电量x(度)与应付电费y(元)的关系如图所示.
(1)请你根据图象所描述的信息,分别求出当0≤x≤50 和x>50时,y与x的函数解析式;
(2)根据你的分析:当每月用电量不超过50度时,收费标准是多少?当每月用电量超过50度时,收费标准又是多少?
我的反思(收获,不足)
分层作业
必做(教材 智慧学习 配套) 选做
参考答案:
课前检测
试题分析:把点(9,0)和点(24,20)代入一次函数的解析式,列出关于k和b的方程组,求出未知数便可求出其解析式.
详解:根据题意,得
,解得.
∴这条直线的解析式为y=x﹣12.
自学自测
试题分析:(1)根据行驶里程的多少进行分别计算即可;(2)本题为分段函数,根据题意列出函数解析式即可;(3)某顾客走了30千米,也就是函数式里的x=30代入求出y的值即可.
详解:(1)小明乘出租车行驶了2千米,收费应按起步价8元;
若行驶了5千米,则应收费8+(5-3)×2.6=13.2元.
(2)由题意,得
y=,即y=.
(3)x=30时y=2.6×30+0.2=78.2(元)
乘坐出租车行驶30千米应付78.2元.
问题1
试题分析:用C和F分别表示摄氏温度和华氏温度,由于摄氏温度与华氏温度的关系近似地为一次函数关系,因此可设C=kF+b,根据题意目中的数据可以求得C与F的函数关系式.
详解:用C和F分别表示摄氏温度和华氏温度,设C=kF+b,由题意得
,解得,
即C与F的函数关系式是C=.
精讲点拨
例1 试题分析:(1)当这个月用水量不超过8m3时,本月水费按每立方米收费1.00元,再加上每立方米0.3元的城市污水处理费计算;当这个月用水量超过8m3时,本月水费分两部分计算:8×(1+0.3)+超过8 m3的部分的收费;
(2)将x=10代入解析式即可求得所需的费用;
(3)设这个月用水为xm3,将y=26.6代入,列方程求解.
详解:(1)当x不超过8m3时,这个月水费为:(1+0.3)x=1.3x元;当x超过8m3时,这个月水费为:8×(1+0.3)+(x﹣8)(1.5+1.2)=2.7x﹣11.2(元).
即y=.
(2)当x=10时,y=2.7×10-11.2=15.8(元);
即该用户某月用水10立方米时,应缴水费15.8元.
(3)设这个月所用水为xm3,
根据题意得:2.7x-11.2=26.6
解得:x=14.
答:当这个月所付水费为26.6元时,这个月所用水为14m3.
变式训练
1.试题分析:(1)根据题意列出一次函数解析式,将两点坐标代入解析式即可求得答案;
(2)令y=0便可解得一箱油可供拖拉机工作8小时.
详解:(1)设解析式为y=kx+b,将x1=2,y1=30和x2=6,y2=10代入,得
,解得.
所以解析式为y=﹣5x+40;
(2)当y=0时,即 ﹣5x+40=0.
∴x=8(小时).
答:一箱油可供拖拉机工作8小时.
2.试题分析:(1)由函数图象可以直接得出服药后2时,血液中含药量最高为每毫升6微克,而得出结论;
(2)设直线AB的解析式为y=kx+b,由待定系数法求出解析式,当x=5时代入解析式求出y的值即可;
(3)当x≤2时,设y与x之间的函数关系式y=k1x,由待定系数法求出其解即可;
(4)当x≥2时,y与x之间的函数关系式是y=kx+b,由待定系数法求出其解即可;
(5)当y=3时分别代入(3)、(4)的两个解析式求出x的值就可以求出结论.
详解:(1)由函数图象,得
服药后2小时,血液中含药量最高为每毫升6微克. 故答案为:2,6;
(2)设直线AB的解析式为y=kx+b,由题意,得
,解得:,
∴y=﹣x+8,
当x=5时,y=3, 故答案为:3;
(3)当x≤2时,设y与x之间的函数关系式y=k1x,由题意,得
6=2k1,
解得:k1=3, ∴y=3x.
故答案为:y=3x;
(4)当x≥2时,y与x之间的函数关系式是y=kx+b,由题意,得
, 解得:,
∴y=﹣x+8,
故答案为:y=﹣x+8;
(5)由题意,得
当y=3时,由3x=3,得x=1;
由-x+8=3,得x=5.
∴有效时间范围是:5﹣1=4小时. 故答案为:4.
星级达标:
1.试题分析:由题意可知汽车2小时形式的路程为160千米,从而可求得汽车行驶的速度,然后依据路程÷速度=时间可求得按照原来速度形式所需要的时间,故此可求得提前的时间.
详解:320﹣160=160千米,
160÷2=80千米/小时.
320÷80=4小时.
6﹣4=2.
故答案为:2.
2.试题分析:(1)由图象可知当x=0时,y=40;当x=4时,y=120,然后利用待定系数法求一次函数解析式解答即可;
(2)把y=200代入函数解析式进行计算即可得解.
详解:(1)由题意,当x=0时,y=40;当x=4时,y=120,
设y和x的关系式为y=kx+b(k≠0),
则, 解得,
所以 y=20x+40;
(2)存够200元时,20x+40=200,
解得 x=8,
即:小明经过8个月才能存够200元.
3.试题分析:根据实验室温度T=20+每小时升高的温度×时间,即可得到函数解析式,然后根据函数图象的画法画出图象即可.
详解:实验室温度T(单位:℃)关于时间t(单位:h)的函数解析式为:
当0≤t≤2时,T=20;
当2<t≤4时,T=5t+20.
函数图象如图所示:
4.试题分析:(1)0≤x≤50时,函数为正比例函数,把(50,25)代入正比例函数解析式即可.x>50时,为一次函数解析式,把(50,25),(100,70)代入即可求得;
(2)不超过50度时,让总价25÷数量50即可,超过50度时,超过部分的付费为(70﹣25)÷(100﹣50)=0.9.
详解:(1)①当月用电量0≤x≤50时,y是x的正比例函数,
设y=k1x,∵当x=50时,y=25,
∴25=50k1,∴ ∴;
②当月用电量x>50时,y是x的一次函数,
设y=k2x+b,∵当x=50时,y=25;当x=100时,y=70,
∴, ∴. ∴y=0.9x﹣20.
(2)当每月用电量不超过50度时,收费标准是:每度0.50元;当每月用电量超过50度时,收费标准是:其中的50度每度0.5元,超过部分每度0.9元.
第4课时 一次函数与实际问题
学习目标:
1.巩固一次函数知识,灵活运用变量关系解决相关的实际问题.
2.有机地把各种数学模型通过函数统一起来,提高解决实际问题的能力.
3.认识数学在现实生活中的意义,提高运用数学知识解决实际问题的能力.
学习重点:学会用一次函数解决实际问题.
一、课前检测
已知直线经过点(9,0)和点(24,20),求这条直线的函数解析式.
二、温故知新
1.一次函数的解析式的一般形式为 .
2.画函数图象的一般步骤是 、 、 .
3.说一说用待定系数法求一次函数解析式的步骤.
三、预习导航(预习教材第94-95页,标出你认为重要的关键词)
1.已知
(1)分别求出当x=1,x=5时y的值;
(2)y是x的函数吗?它与一次函数有何区别?
(3)若y是x的函数,你能画出它的函数图象吗?
2.自主归纳:
与上题中形式相同的函数叫做分段函数.
注意:(1)它是一个函数,不要误以为是两个函数;
(2)对于不同取值范围的自变量,它所对应的函数解析式不同;
(3)它的函数图象也是由两部分组成.
四、自学自测
某市出租车计费标准为:起步价8元(3千米及以内),超过3千米的部分按每千米2.6元计算,设行驶的路程为x千米,应交的车费为y元.
(1)若小明乘出租车行驶了2千米,应收费______元;
若行驶5千米,应收费______元;
(2)请写出当 0<x≤3和x>3时y与x之间的函数解析式;
(3)若某顾客走了30千米,你能算出他应付多少元钱吗?
五、我的疑惑(反思)
__________________________________________________________________________________________________________________________________________________
要点探究
探究点1:一次函数与实际问题
问题1 温度的度量有两种:摄氏温度和华氏温度.
水的沸点温度是100℃,用华氏温度度量为212℉;水的冰点温度是0℃,用华氏温度度量为32 ℉.已知摄氏温度与华氏温度的关系近似地为一次函数关系,你能不能想出一个办法方便地把华氏温度换算成摄氏温度?
方法总结:已知两个变量是一次函数关系,直接设其解析式,然后根据题目两个已知条件,用待定系数法求解即可.
二、精讲点拨
例1 为节约用水,某市制定以下用水收费标准,每户每月用水不超过8立方米,每立方米收取1元外加0.3元的污水处理费;超过8立方米时,超过部分每立方米收取1.5元外加1.2元污水处理费,现设一户每月用水x立方米,应缴水费y元.
(1)求出y关于x的函数解析式;
(2)该市一户某月若用水10立方米时,求应缴水费多少元?
(3)该市一户某月缴水费26.6元,求该户这月用水量.
方法总结:不同取值范围的自变量所对应的函数解析式不同是分段函数.利用分段函数解决实际问题时,注意自变量要与解析式对应.
三、变式训练
1.某种拖拉机的油箱可储油40L,加满油并开始工作后,油箱中的剩余油量y(L)与工作时间x(h) 之间为一次函数关系,函数图象如图所示.
(1)求y关于x的函数解析式;
(2)一箱油可供拖拉机工作几小时?
2. 某医药研究所开发了一种新药,在实际验药时发现,如果成人按规定剂量服用,那么每毫升血液中含药量y(毫克)随时间x(时)的变化情况如图所示,当成年人按规定剂量服药后.
(1)服药后_____时,血液中含药量最高,达到每毫升_____毫克,接着逐步衰弱.
(2)服药5时,血液中含药量为每毫升____毫克.
(3)当x≤2时y与x之间的函数解析式是___________.
(4)当x≥2时y与x之间的函数解析式是___________.
(5)如果每毫升血液中含药量3毫克或3毫克以上时,治疗疾病最有效,那么这个有效时间是______时.
四、课堂小结
一次函数与实际问题 1.根据实际问题直接列解析式
2.设解析式,再利用待定系数法求解析式
3.分段函数的应用
★1.一辆汽车由A地开往B地,它距离B地的路程s(km)与行驶时间t(h)的关系如图所示,如果汽车一直快速行驶,那么可以提前______小时到达B地.
★2.小明将父母给的零用钱按每月相等的数额存在储蓄盒内,准备捐给希望工程,盒内钱数y(元)与存钱月数 x(月)之间的关系如图所示,根据下图回答下列问题:
求出y关于x的函数解析式.
根据关系式计算,小明经过几个月才能存够200元?
★★3.一个试验室在0:00—2:00保持20℃的恒温,在2:00—4:00匀速升温,每小时升高5℃.写出试验室温度T(单位:℃)关于时间t(单位:h)的函数解析式,并画出函数图象.
★★★4.近几年来,由于经济和社会发展迅速,用电量越来越多.为缓解用电紧张,某电力公司特制定了新的用电收费标准,每月用电量x(度)与应付电费y(元)的关系如图所示.
(1)请你根据图象所描述的信息,分别求出当0≤x≤50 和x>50时,y与x的函数解析式;
(2)根据你的分析:当每月用电量不超过50度时,收费标准是多少?当每月用电量超过50度时,收费标准又是多少?
我的反思(收获,不足)
分层作业
必做(教材 智慧学习 配套) 选做
参考答案:
课前检测
试题分析:把点(9,0)和点(24,20)代入一次函数的解析式,列出关于k和b的方程组,求出未知数便可求出其解析式.
详解:根据题意,得
,解得.
∴这条直线的解析式为y=x﹣12.
自学自测
试题分析:(1)根据行驶里程的多少进行分别计算即可;(2)本题为分段函数,根据题意列出函数解析式即可;(3)某顾客走了30千米,也就是函数式里的x=30代入求出y的值即可.
详解:(1)小明乘出租车行驶了2千米,收费应按起步价8元;
若行驶了5千米,则应收费8+(5-3)×2.6=13.2元.
(2)由题意,得
y=,即y=.
(3)x=30时y=2.6×30+0.2=78.2(元)
乘坐出租车行驶30千米应付78.2元.
问题1
试题分析:用C和F分别表示摄氏温度和华氏温度,由于摄氏温度与华氏温度的关系近似地为一次函数关系,因此可设C=kF+b,根据题意目中的数据可以求得C与F的函数关系式.
详解:用C和F分别表示摄氏温度和华氏温度,设C=kF+b,由题意得
,解得,
即C与F的函数关系式是C=.
精讲点拨
例1 试题分析:(1)当这个月用水量不超过8m3时,本月水费按每立方米收费1.00元,再加上每立方米0.3元的城市污水处理费计算;当这个月用水量超过8m3时,本月水费分两部分计算:8×(1+0.3)+超过8 m3的部分的收费;
(2)将x=10代入解析式即可求得所需的费用;
(3)设这个月用水为xm3,将y=26.6代入,列方程求解.
详解:(1)当x不超过8m3时,这个月水费为:(1+0.3)x=1.3x元;当x超过8m3时,这个月水费为:8×(1+0.3)+(x﹣8)(1.5+1.2)=2.7x﹣11.2(元).
即y=.
(2)当x=10时,y=2.7×10-11.2=15.8(元);
即该用户某月用水10立方米时,应缴水费15.8元.
(3)设这个月所用水为xm3,
根据题意得:2.7x-11.2=26.6
解得:x=14.
答:当这个月所付水费为26.6元时,这个月所用水为14m3.
变式训练
1.试题分析:(1)根据题意列出一次函数解析式,将两点坐标代入解析式即可求得答案;
(2)令y=0便可解得一箱油可供拖拉机工作8小时.
详解:(1)设解析式为y=kx+b,将x1=2,y1=30和x2=6,y2=10代入,得
,解得.
所以解析式为y=﹣5x+40;
(2)当y=0时,即 ﹣5x+40=0.
∴x=8(小时).
答:一箱油可供拖拉机工作8小时.
2.试题分析:(1)由函数图象可以直接得出服药后2时,血液中含药量最高为每毫升6微克,而得出结论;
(2)设直线AB的解析式为y=kx+b,由待定系数法求出解析式,当x=5时代入解析式求出y的值即可;
(3)当x≤2时,设y与x之间的函数关系式y=k1x,由待定系数法求出其解即可;
(4)当x≥2时,y与x之间的函数关系式是y=kx+b,由待定系数法求出其解即可;
(5)当y=3时分别代入(3)、(4)的两个解析式求出x的值就可以求出结论.
详解:(1)由函数图象,得
服药后2小时,血液中含药量最高为每毫升6微克. 故答案为:2,6;
(2)设直线AB的解析式为y=kx+b,由题意,得
,解得:,
∴y=﹣x+8,
当x=5时,y=3, 故答案为:3;
(3)当x≤2时,设y与x之间的函数关系式y=k1x,由题意,得
6=2k1,
解得:k1=3, ∴y=3x.
故答案为:y=3x;
(4)当x≥2时,y与x之间的函数关系式是y=kx+b,由题意,得
, 解得:,
∴y=﹣x+8,
故答案为:y=﹣x+8;
(5)由题意,得
当y=3时,由3x=3,得x=1;
由-x+8=3,得x=5.
∴有效时间范围是:5﹣1=4小时. 故答案为:4.
星级达标:
1.试题分析:由题意可知汽车2小时形式的路程为160千米,从而可求得汽车行驶的速度,然后依据路程÷速度=时间可求得按照原来速度形式所需要的时间,故此可求得提前的时间.
详解:320﹣160=160千米,
160÷2=80千米/小时.
320÷80=4小时.
6﹣4=2.
故答案为:2.
2.试题分析:(1)由图象可知当x=0时,y=40;当x=4时,y=120,然后利用待定系数法求一次函数解析式解答即可;
(2)把y=200代入函数解析式进行计算即可得解.
详解:(1)由题意,当x=0时,y=40;当x=4时,y=120,
设y和x的关系式为y=kx+b(k≠0),
则, 解得,
所以 y=20x+40;
(2)存够200元时,20x+40=200,
解得 x=8,
即:小明经过8个月才能存够200元.
3.试题分析:根据实验室温度T=20+每小时升高的温度×时间,即可得到函数解析式,然后根据函数图象的画法画出图象即可.
详解:实验室温度T(单位:℃)关于时间t(单位:h)的函数解析式为:
当0≤t≤2时,T=20;
当2<t≤4时,T=5t+20.
函数图象如图所示:
4.试题分析:(1)0≤x≤50时,函数为正比例函数,把(50,25)代入正比例函数解析式即可.x>50时,为一次函数解析式,把(50,25),(100,70)代入即可求得;
(2)不超过50度时,让总价25÷数量50即可,超过50度时,超过部分的付费为(70﹣25)÷(100﹣50)=0.9.
详解:(1)①当月用电量0≤x≤50时,y是x的正比例函数,
设y=k1x,∵当x=50时,y=25,
∴25=50k1,∴ ∴;
②当月用电量x>50时,y是x的一次函数,
设y=k2x+b,∵当x=50时,y=25;当x=100时,y=70,
∴, ∴. ∴y=0.9x﹣20.
(2)当每月用电量不超过50度时,收费标准是:每度0.50元;当每月用电量超过50度时,收费标准是:其中的50度每度0.5元,超过部分每度0.9元.
