19.2.2用待定系数法求一次函数的解析式-2020-2021学年人教版八年级数学下册导学案(Word版含详解)
文档属性
| 名称 | 19.2.2用待定系数法求一次函数的解析式-2020-2021学年人教版八年级数学下册导学案(Word版含详解) |  | |
| 格式 | doc | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-31 10:58:33 | ||
图片预览



文档简介
19.2.2 一次函数
第3课时 用待定系数法求一次函数的解析式
学习目标:
1.弄清楚待定系数法的意义.
2.会用待定系数法求一次函数的解析式.
学习重点:会用待定系数法求一次函数的解析式.
一、课前检测
已知函数y=(m+2)x+m-2.
(1)若函数图象经过原点,求m的值;
(2)若函数图象平行于直线y=-2x+1,求m的值;
(3)若这个函数是一次函数,且y随x的增大而减小,求m的取值范围.
二、温故知新
1.一次函数的定义:一般地,形如 的函数,叫做一次函数,其中x是自变量;当 时,一次函数就成为正比例函数,所以说正比例函数是一种 的一次函数.
2.在直线中,k ,b的取值决定直线的位置:k确定函数的
性,b确定图象与 的交点.
三、预习导航(预习教材第93-94页,标出你认为重要的关键词)
1.已知:正比例函数的图像过点(3,5),求这个正比例函数的解析式.
解: 设正比例函数的解析式为y=kx(k≠0)
∵图像过点( )
∴5=3k
∴k=
∴y= x
2.已知一次函数y=kx+b中,当x=3时,y=5;当x=-4时,y=-9.
解:由已知条件x=3时,y=5,得 ,
由已知条件x=-4时,y=-9,得 ,
两个条件都要满足,即解关于x的二元一次方程组: ,
解得 .
所以,一次函数解析式为 .
自主归纳:
(1)求一次函数的解析式时需要 个条件,求正比例函数需要 个条件.
(2)像上例这样先设出 ,再根据条件确定解析式中 ,从而具体写出这个式子的方法,叫做 .
四、自学自测
根据下列条件求出直线的解析式.
直线y=kx+5经过点(-2,-1);
(2)直线与坐标轴的交点分别是(0,2),(3,0).
五、我的疑惑(反思)
__________________________________________________________________________________________________________________________________________________
要点探究
探究点1:用待定系数法求一次函数的解析式
问题1:用待定系数法求一次函数的解析式需要哪些步骤?
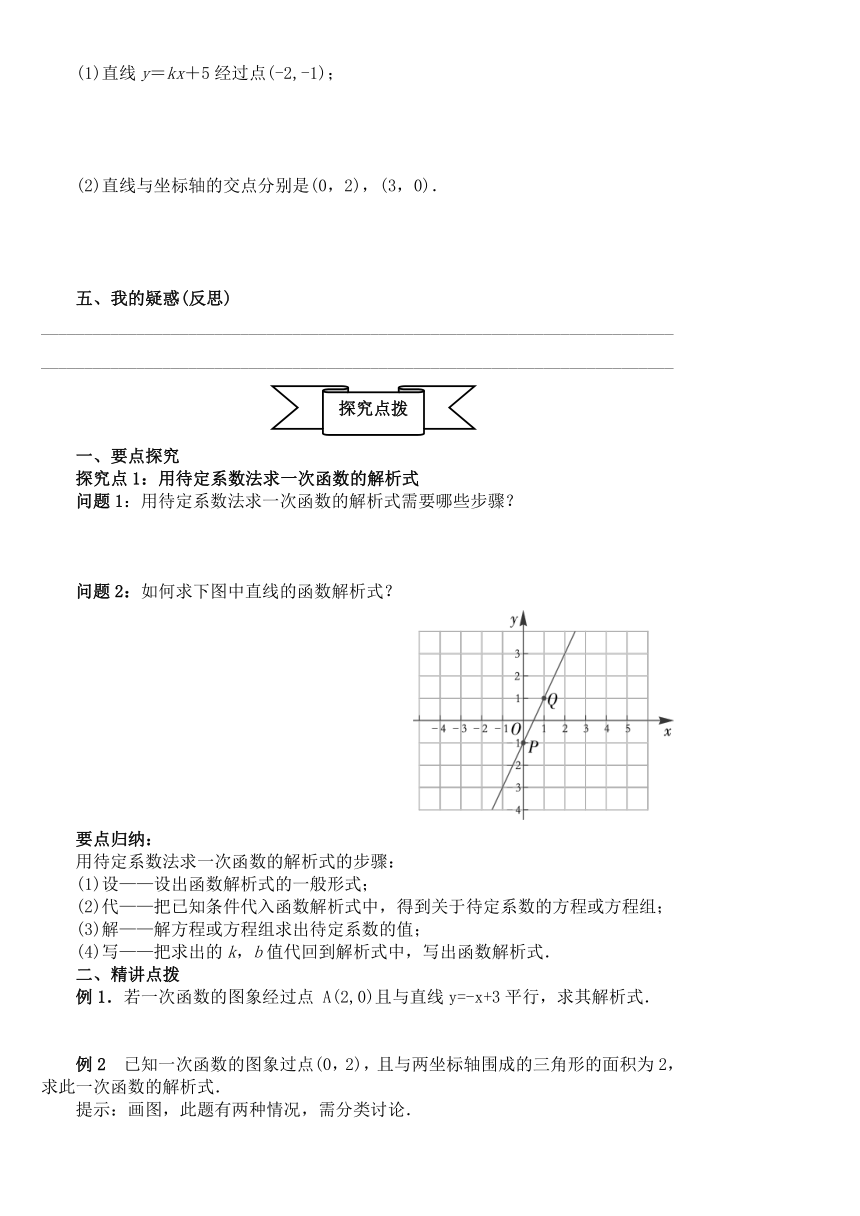
问题2:如何求下图中直线的函数解析式?
要点归纳:
用待定系数法求一次函数的解析式的步骤:
(1)设——设出函数解析式的一般形式;
(2)代——把已知条件代入函数解析式中,得到关于待定系数的方程或方程组;
(3)解——解方程或方程组求出待定系数的值;
(4)写——把求出的k,b值代回到解析式中,写出函数解析式.
二、精讲点拨
例1.若一次函数的图象经过点 A(2,0)且与直线y=-x+3平行,求其解析式.
例2 已知一次函数的图象过点(0,2),且与两坐标轴围成的三角形的面积为2,求此一次函数的解析式.
提示:画图,此题有两种情况,需分类讨论.
方法总结:
三、变式训练
1.若y+3与x成正比例,且x=2时,y=5,则x=5时,y= .
2.写出经过点(1,2)的直线的解析式 (写出一个即可).
3.正比例函数y=k1x与一次函数y=k2x+b的图象如图所示,它们的交点A的坐标为(3,4),并且OB=5.
(1)你能求出这两个函数的解析式吗?
(2)△AOB的面积是多少呢?
四、课堂小结
用待定系数法求一次函数的解析式
步骤 (1)设——设出函数解析式的一般形式
(2)代——把已知条件代入函数解析式中,得到关于待定系数的方程或方程组
(3)解——解方程或方程组求出待定系数的值
(4)写——把求出的k,b值代回到解析式中,写出函数解析式.
★1.一次函数y=kx+b(k≠0)的图象如图所示,则下列结论正确的是 ( )
A.k=2 B.k=3 C.b=2 D.b=3
第1题图 第2题图
★2.如图,直线是一次函数y=kx+b的图象,填空:
(1)b=______,k=______;
(2)当x=30时,y=______;
(3)当y=30时,x=______.
★3.某一次函数的图象经过点(1,2),且y随x的增大而减小,则这个函数的解析式可能为( )
A.y=2x+4 B.y=3x-1 C.y=-3x+1 D.y=-2x+4
★4.已知直线l与直线y=-2x平行,且与y轴交于点(0,5),求直线l的解析式.
★★5.若一直线与另一直线y=-3x+2交于y轴同一点,且过(2,-6),你能求出这条直线的解析式吗?
★★★6.已知一次函数y=kx+b(k≠0)的自变量的取值范围是-3≤x≤6,相应函数值的范围是-5≤y≤-2 ,求这个函数的解析式.
我的反思(收获,不足)
分层作业
必做(教材 智慧学习 配套) 选做
参考答案:
课前检测
试题分析:(1)令x=0,y=0求出m的值即可;
(2)根据互相平行的两条直线比例系数k相等,求出m的值即可;
(3)根据一次函数的性质求出m的取值范围.
详解:(1)∵函数y=(m+2)x+m﹣2的图象经过原点,
∴当x=0时y=0,
即m﹣2=0,
解得m=2;
(2)∵函数y=(m+2)x+m﹣2的图象与直线y=-2x+1平行,
∴m+2=-2,
解得m=-4;
(3)∵这个函数是一次函数,且y随着x的增大而减小,
∴m+2<0,
解得m<﹣2.
自学自测
试题分析:(1)直接把(﹣2,﹣1)代入y=kx+5求出k即可;
(2)设一次函数解析式为y=ax+b,再把(0,2)、(3,0)代入得到关于a、b的方程组,然后解方程组求出a、b的值,即可得到一次函数解析式.
详解:(1)把(﹣2,﹣1)代入y=kx+5得﹣2k+5=﹣1,解得k=3,
所以直线解析式为y=3x+5;
(2)设一次函数解析式为y=ax+b,把(0,2)、(3,0)代入得
,解得.
所以一次函数解析式为y=﹣x+2.
精讲点拨
例1.试题分析:设一次函数的表达式为y=kx+b,由于它的图象与直线y=﹣x+3平行,可知k=﹣1,再由图象过点A(2,0),可求出b,从而可求表达式;
详解:设一次函数的表达式为y=kx+b,由题意得
,解得,
故这个一次函数的表达式为:y=﹣x+2.
例2 试题分析:先根据一次函数y=kx+b(k≠0)图象过点(0,2)可知b=2,再用k表示出函数图象与x轴的交点,利用三角形的面积公式求解即可.
详解:∵一次函数y=kx+b(k≠0)图象过点(0,2),
∴b=2,
令y=0,则x=﹣,
∵函数图象与两坐标轴围成的三角形面积为2,
∴×2×|﹣|=2,即|﹣|=2,
当k>0时,=2,解得k=1;
当k<0时,﹣=2,解得k=﹣1.
故此函数的解析式为:y=x+2或y=﹣x+2.
变式训练
1.试题分析:首先设y+3=kx,再代入x=2,y=5,然后可得k的值,进而可得答案.
详解:设y+3=kx,
∵当x=2时,y=5,
∴5+3=2k,
解得:k=4,
∴y+3=4x, 即y=4x﹣3.
∴当x=5时,y=4×5-3=17.
故答案为17.
2.试题分析:由图象经过(1,2)点可得出k与b的关系式b+k=2,即可任意写出一个满足这个关系的一次函数解析式.
详解:设函数的解析式为y=kx+b,
将(1,2)代入
得b+k=2,若k=-1,则b=3.
故答案可为:y=﹣x+3.
3.试题分析:(1)将点A坐标代入y=k1x求得k1即可知正比例函数解析式;将A、B两点坐标代入y=k2x+b解方程组可得k2、b的值即可知一次函数解析式;
(2)将OB当做三角形的底,根据面积公式计算可得.
详解:(1)将点A(3,4)代入y=k1x,得:3k1=4,
解得:k1=,
故正比例函数解析式为:y=x,
∵OB=5,
∴点B坐标为(0,﹣5),
将点A(3,4)、B(0,﹣5)代入y=k2x+b,
得:, 解得:,
故一次函数解析式为:y=3x﹣5;
(2)S△AOB=×OB×xA=×5×3=,
故△OAB的面积为.
星级达标:
1.试题分析:直接把点(2,0),(0,3)代入一次函数y=kx+b(k≠0),求出k,b的值即可.
详解:由函数图象可知函数图象过点(2,0),(0,3),
∴,解得.
故选:D.
2.试题分析:(1)根据图象过点(3,0)和(0,2)可得出函数解析式;
(2)把x=30代入解析式即可求得;
(3)把y=30代入解析式即可求得.
详解:(1)根据图形可得函数过点(3,0)和(0,2),
将这两点代入得:,
解得:k=﹣,b=2.
(2)由(1)得函数解析式为:y=﹣x+2,
∴当x=30时,y=﹣×30+2=﹣18;
(3)当y=30时,则30=﹣x+2,
解得x=﹣42.
故答案为:2,﹣;﹣18;﹣42.
3.试题分析:设一次函数关系式为y=kx+b,y随x增大而减小,则k<0;图象经过点(1,2),可得k、b之间的关系式.综合二者取值即可.
详解:设一次函数关系式为y=kx+b,
∵图象经过点(1,2),
∴k+b=2;
∵y随x增大而减小,
∴k<0.
即k取负数,满足k+b=2的k、b的取值都可以.
故选:D.
4.试题分析:根据直线与直线y=﹣2x平行,直线的解析式的一次项系数等于﹣2,则设直线的解析式为:y=﹣2x+b,再由与y轴交于点(0,5),可得直线的解析式.
详解:∵直线与直线y=﹣2x平行,
∴设直线的解析式为:y=﹣2x+b,
∵与y轴交于点(0,5),
∴5=﹣2×0+b,
∴b=5,
∴y=﹣2x+5,
∴直线的表达式为:y=﹣2x+5.
5.试题分析:由直线y=kx+b与直线y=﹣3x+2交于y轴上同一点,即可求出交点,再根据经过点(2,﹣6)即可列出关于k、b的方程组,解之即可得出答案.
详解:由题意y=kx+b与y=﹣3x+2交于y轴同一点,
可知该交点为(0,2).
又因为y=kx+b经过点(2,-6),
∴,解得.
∴直线的解析式为y=﹣4x+2.
6.试题分析:根据一次函数的增减性,可知本题分两种情况:①当k>0时,y随x的增大而增大,把x=﹣3,y=﹣5;x=6,y=﹣2代入一次函数的解析式y=kx+b,运用待定系数法即可求出函数的解析式;②当k<0时,y随x的增大而减小,把x=﹣3,y=﹣2;x=6,y=﹣5代入一次函数的解析式y=kx+b,运用待定系数法即可求出函数的解析式.
详解:分两种情况:
①当k>0时,把x=﹣3,y=﹣5;x=6,y=﹣2代入一次函数的解析式y=kx+b,
得,
解得,
则这个函数的解析式是y=x﹣4(﹣3≤x≤6);
②当k<0时,把x=﹣3,y=﹣2;x=6,y=﹣5代入一次函数的解析式y=kx+b,
得,
解得,
则这个函数的解析式是y=﹣x﹣3(﹣3≤x≤6).
故这个函数的解析式是y=x﹣4(﹣3≤x≤6)或者y=﹣x﹣3(﹣3≤x≤6).
第3课时 用待定系数法求一次函数的解析式
学习目标:
1.弄清楚待定系数法的意义.
2.会用待定系数法求一次函数的解析式.
学习重点:会用待定系数法求一次函数的解析式.
一、课前检测
已知函数y=(m+2)x+m-2.
(1)若函数图象经过原点,求m的值;
(2)若函数图象平行于直线y=-2x+1,求m的值;
(3)若这个函数是一次函数,且y随x的增大而减小,求m的取值范围.
二、温故知新
1.一次函数的定义:一般地,形如 的函数,叫做一次函数,其中x是自变量;当 时,一次函数就成为正比例函数,所以说正比例函数是一种 的一次函数.
2.在直线中,k ,b的取值决定直线的位置:k确定函数的
性,b确定图象与 的交点.
三、预习导航(预习教材第93-94页,标出你认为重要的关键词)
1.已知:正比例函数的图像过点(3,5),求这个正比例函数的解析式.
解: 设正比例函数的解析式为y=kx(k≠0)
∵图像过点( )
∴5=3k
∴k=
∴y= x
2.已知一次函数y=kx+b中,当x=3时,y=5;当x=-4时,y=-9.
解:由已知条件x=3时,y=5,得 ,
由已知条件x=-4时,y=-9,得 ,
两个条件都要满足,即解关于x的二元一次方程组: ,
解得 .
所以,一次函数解析式为 .
自主归纳:
(1)求一次函数的解析式时需要 个条件,求正比例函数需要 个条件.
(2)像上例这样先设出 ,再根据条件确定解析式中 ,从而具体写出这个式子的方法,叫做 .
四、自学自测
根据下列条件求出直线的解析式.
直线y=kx+5经过点(-2,-1);
(2)直线与坐标轴的交点分别是(0,2),(3,0).
五、我的疑惑(反思)
__________________________________________________________________________________________________________________________________________________
要点探究
探究点1:用待定系数法求一次函数的解析式
问题1:用待定系数法求一次函数的解析式需要哪些步骤?
问题2:如何求下图中直线的函数解析式?
要点归纳:
用待定系数法求一次函数的解析式的步骤:
(1)设——设出函数解析式的一般形式;
(2)代——把已知条件代入函数解析式中,得到关于待定系数的方程或方程组;
(3)解——解方程或方程组求出待定系数的值;
(4)写——把求出的k,b值代回到解析式中,写出函数解析式.
二、精讲点拨
例1.若一次函数的图象经过点 A(2,0)且与直线y=-x+3平行,求其解析式.
例2 已知一次函数的图象过点(0,2),且与两坐标轴围成的三角形的面积为2,求此一次函数的解析式.
提示:画图,此题有两种情况,需分类讨论.
方法总结:
三、变式训练
1.若y+3与x成正比例,且x=2时,y=5,则x=5时,y= .
2.写出经过点(1,2)的直线的解析式 (写出一个即可).
3.正比例函数y=k1x与一次函数y=k2x+b的图象如图所示,它们的交点A的坐标为(3,4),并且OB=5.
(1)你能求出这两个函数的解析式吗?
(2)△AOB的面积是多少呢?
四、课堂小结
用待定系数法求一次函数的解析式
步骤 (1)设——设出函数解析式的一般形式
(2)代——把已知条件代入函数解析式中,得到关于待定系数的方程或方程组
(3)解——解方程或方程组求出待定系数的值
(4)写——把求出的k,b值代回到解析式中,写出函数解析式.
★1.一次函数y=kx+b(k≠0)的图象如图所示,则下列结论正确的是 ( )
A.k=2 B.k=3 C.b=2 D.b=3
第1题图 第2题图
★2.如图,直线是一次函数y=kx+b的图象,填空:
(1)b=______,k=______;
(2)当x=30时,y=______;
(3)当y=30时,x=______.
★3.某一次函数的图象经过点(1,2),且y随x的增大而减小,则这个函数的解析式可能为( )
A.y=2x+4 B.y=3x-1 C.y=-3x+1 D.y=-2x+4
★4.已知直线l与直线y=-2x平行,且与y轴交于点(0,5),求直线l的解析式.
★★5.若一直线与另一直线y=-3x+2交于y轴同一点,且过(2,-6),你能求出这条直线的解析式吗?
★★★6.已知一次函数y=kx+b(k≠0)的自变量的取值范围是-3≤x≤6,相应函数值的范围是-5≤y≤-2 ,求这个函数的解析式.
我的反思(收获,不足)
分层作业
必做(教材 智慧学习 配套) 选做
参考答案:
课前检测
试题分析:(1)令x=0,y=0求出m的值即可;
(2)根据互相平行的两条直线比例系数k相等,求出m的值即可;
(3)根据一次函数的性质求出m的取值范围.
详解:(1)∵函数y=(m+2)x+m﹣2的图象经过原点,
∴当x=0时y=0,
即m﹣2=0,
解得m=2;
(2)∵函数y=(m+2)x+m﹣2的图象与直线y=-2x+1平行,
∴m+2=-2,
解得m=-4;
(3)∵这个函数是一次函数,且y随着x的增大而减小,
∴m+2<0,
解得m<﹣2.
自学自测
试题分析:(1)直接把(﹣2,﹣1)代入y=kx+5求出k即可;
(2)设一次函数解析式为y=ax+b,再把(0,2)、(3,0)代入得到关于a、b的方程组,然后解方程组求出a、b的值,即可得到一次函数解析式.
详解:(1)把(﹣2,﹣1)代入y=kx+5得﹣2k+5=﹣1,解得k=3,
所以直线解析式为y=3x+5;
(2)设一次函数解析式为y=ax+b,把(0,2)、(3,0)代入得
,解得.
所以一次函数解析式为y=﹣x+2.
精讲点拨
例1.试题分析:设一次函数的表达式为y=kx+b,由于它的图象与直线y=﹣x+3平行,可知k=﹣1,再由图象过点A(2,0),可求出b,从而可求表达式;
详解:设一次函数的表达式为y=kx+b,由题意得
,解得,
故这个一次函数的表达式为:y=﹣x+2.
例2 试题分析:先根据一次函数y=kx+b(k≠0)图象过点(0,2)可知b=2,再用k表示出函数图象与x轴的交点,利用三角形的面积公式求解即可.
详解:∵一次函数y=kx+b(k≠0)图象过点(0,2),
∴b=2,
令y=0,则x=﹣,
∵函数图象与两坐标轴围成的三角形面积为2,
∴×2×|﹣|=2,即|﹣|=2,
当k>0时,=2,解得k=1;
当k<0时,﹣=2,解得k=﹣1.
故此函数的解析式为:y=x+2或y=﹣x+2.
变式训练
1.试题分析:首先设y+3=kx,再代入x=2,y=5,然后可得k的值,进而可得答案.
详解:设y+3=kx,
∵当x=2时,y=5,
∴5+3=2k,
解得:k=4,
∴y+3=4x, 即y=4x﹣3.
∴当x=5时,y=4×5-3=17.
故答案为17.
2.试题分析:由图象经过(1,2)点可得出k与b的关系式b+k=2,即可任意写出一个满足这个关系的一次函数解析式.
详解:设函数的解析式为y=kx+b,
将(1,2)代入
得b+k=2,若k=-1,则b=3.
故答案可为:y=﹣x+3.
3.试题分析:(1)将点A坐标代入y=k1x求得k1即可知正比例函数解析式;将A、B两点坐标代入y=k2x+b解方程组可得k2、b的值即可知一次函数解析式;
(2)将OB当做三角形的底,根据面积公式计算可得.
详解:(1)将点A(3,4)代入y=k1x,得:3k1=4,
解得:k1=,
故正比例函数解析式为:y=x,
∵OB=5,
∴点B坐标为(0,﹣5),
将点A(3,4)、B(0,﹣5)代入y=k2x+b,
得:, 解得:,
故一次函数解析式为:y=3x﹣5;
(2)S△AOB=×OB×xA=×5×3=,
故△OAB的面积为.
星级达标:
1.试题分析:直接把点(2,0),(0,3)代入一次函数y=kx+b(k≠0),求出k,b的值即可.
详解:由函数图象可知函数图象过点(2,0),(0,3),
∴,解得.
故选:D.
2.试题分析:(1)根据图象过点(3,0)和(0,2)可得出函数解析式;
(2)把x=30代入解析式即可求得;
(3)把y=30代入解析式即可求得.
详解:(1)根据图形可得函数过点(3,0)和(0,2),
将这两点代入得:,
解得:k=﹣,b=2.
(2)由(1)得函数解析式为:y=﹣x+2,
∴当x=30时,y=﹣×30+2=﹣18;
(3)当y=30时,则30=﹣x+2,
解得x=﹣42.
故答案为:2,﹣;﹣18;﹣42.
3.试题分析:设一次函数关系式为y=kx+b,y随x增大而减小,则k<0;图象经过点(1,2),可得k、b之间的关系式.综合二者取值即可.
详解:设一次函数关系式为y=kx+b,
∵图象经过点(1,2),
∴k+b=2;
∵y随x增大而减小,
∴k<0.
即k取负数,满足k+b=2的k、b的取值都可以.
故选:D.
4.试题分析:根据直线与直线y=﹣2x平行,直线的解析式的一次项系数等于﹣2,则设直线的解析式为:y=﹣2x+b,再由与y轴交于点(0,5),可得直线的解析式.
详解:∵直线与直线y=﹣2x平行,
∴设直线的解析式为:y=﹣2x+b,
∵与y轴交于点(0,5),
∴5=﹣2×0+b,
∴b=5,
∴y=﹣2x+5,
∴直线的表达式为:y=﹣2x+5.
5.试题分析:由直线y=kx+b与直线y=﹣3x+2交于y轴上同一点,即可求出交点,再根据经过点(2,﹣6)即可列出关于k、b的方程组,解之即可得出答案.
详解:由题意y=kx+b与y=﹣3x+2交于y轴同一点,
可知该交点为(0,2).
又因为y=kx+b经过点(2,-6),
∴,解得.
∴直线的解析式为y=﹣4x+2.
6.试题分析:根据一次函数的增减性,可知本题分两种情况:①当k>0时,y随x的增大而增大,把x=﹣3,y=﹣5;x=6,y=﹣2代入一次函数的解析式y=kx+b,运用待定系数法即可求出函数的解析式;②当k<0时,y随x的增大而减小,把x=﹣3,y=﹣2;x=6,y=﹣5代入一次函数的解析式y=kx+b,运用待定系数法即可求出函数的解析式.
详解:分两种情况:
①当k>0时,把x=﹣3,y=﹣5;x=6,y=﹣2代入一次函数的解析式y=kx+b,
得,
解得,
则这个函数的解析式是y=x﹣4(﹣3≤x≤6);
②当k<0时,把x=﹣3,y=﹣2;x=6,y=﹣5代入一次函数的解析式y=kx+b,
得,
解得,
则这个函数的解析式是y=﹣x﹣3(﹣3≤x≤6).
故这个函数的解析式是y=x﹣4(﹣3≤x≤6)或者y=﹣x﹣3(﹣3≤x≤6).
