2020-2021学年人教版八年级数学下册20.1.2中位数和众数导学案(word版含详解)
文档属性
| 名称 | 2020-2021学年人教版八年级数学下册20.1.2中位数和众数导学案(word版含详解) |

|
|
| 格式 | doc | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-31 13:03:45 | ||
图片预览



文档简介
20.1.2数据的集中趋势
第1课时 中位数和众数
学习目标:
1.知道中位数、众数的概念,会求一组数据的中位数、众数.
2.弄清楚中位数、众数的作用,会用中位数、众数分析实际问题.
学习重点:理解中位数、众数的概念,会求一组数据的中位数、众数.
一、课前检测
二、温故知新
1.n个数据a1,a2,a3,a4,…,an的算术平均数 .
2.若n个数x1,x2,…,xn的权分别是w1,w2,…,wn,则__________________叫做这n个数的加权平均数.
3.n个数据:f1个a1,f2个a2,…,fn个an,它的加权平均数为 .
三、预习导航(预习教材第116-118页,标出你认为重要的关键词)
1.下表是某公司员工月收入的资料.
(1)计算这个公司员工月收入的平均数;
(2)如果用(1)算得的平均数反映公司全体员工月收入水平,你认为合适吗?
(3)该公司员工的中等收入水平大概是多少元?你是怎样确定的?
(4)“平均数”和“中等水平”谁更合理地反映了该公司绝大部分员工的月工资水平?这个问题中,中等水平的含义是什么?
2.自主归纳:
(1)将一组数据按照由小到大(或由大到小)的顺序排列:
如果数据的个数是奇数,则称 为这组数据的中位数;
如果数据的个数是偶数,则称 为这组数据的中位数.
(2)一组数据中 的数据称为这组数据的众数.
四、自学自测
1.判断:
(1)一组数据中间的数称为中位数. ( )
(2)一组数据中出现次数最多的数称为这组数据的众数.( )
(3)一组数据中的中位数和众数是唯一的一个数. ( )
(4)一组数据的中位数一定是这组数据中的某个数. ( )
2.求出下面各组数据的中位数和众数:
(1)90,23,27,40,90,18,52,100;
(2)21,15,32,32,46,32,58,64,98.
五、我的疑惑(反思)
__________________________________________________________________________________________________________________________________________________
要点探究
探究点1:中位数
问题1:确定一组数据的中位数时,要注意什么?
问题2:中位数反映的是一组数据的何种特征,它有何意义?
即学即练 在一次男子马拉松长跑比赛中,抽得12名选手所用时间(单位:min)如下:
136 140 129 180 124 154
146 145 158 175 165 148
(1)样本数据(12名选手的成绩)的中位数是多少?
(2)一名选手的成绩是142min,他的成绩如何?
要点提醒:
1.中位数是一个位置代表值(中间数),它是唯一的,且不一定出现在这组数据中.
2.中位数仅与数据的排列位置有关,如果一组数据中有极端数据时,中位数能比平均数更能合理地反映该组数据的整体水平.
3.如果已知一组数据的中位数,那么中位数以上和以下的数据个数相等.
探究点2:众数
问题3:如果小张是该公司的一名普通员工,那么你认为他的月工资最有可能是多少元?
问题4:一组数据的众数一定是唯一的吗?请举例说明.
要点提醒:
1.一组数据的众数可能不止一个,但一定是这组数据的某一个或几个数.
2.一组数据中,若每个数据出现的频数相同,则这组数据没有众数.
二、精讲点拨
例1 已知一组数据10,10,x,8(由大到小排列)的中位数与平均数相等,求x值及这组数据的中位数.
分析:由题意可知最中间两位数是10,x,列方程求解即可.
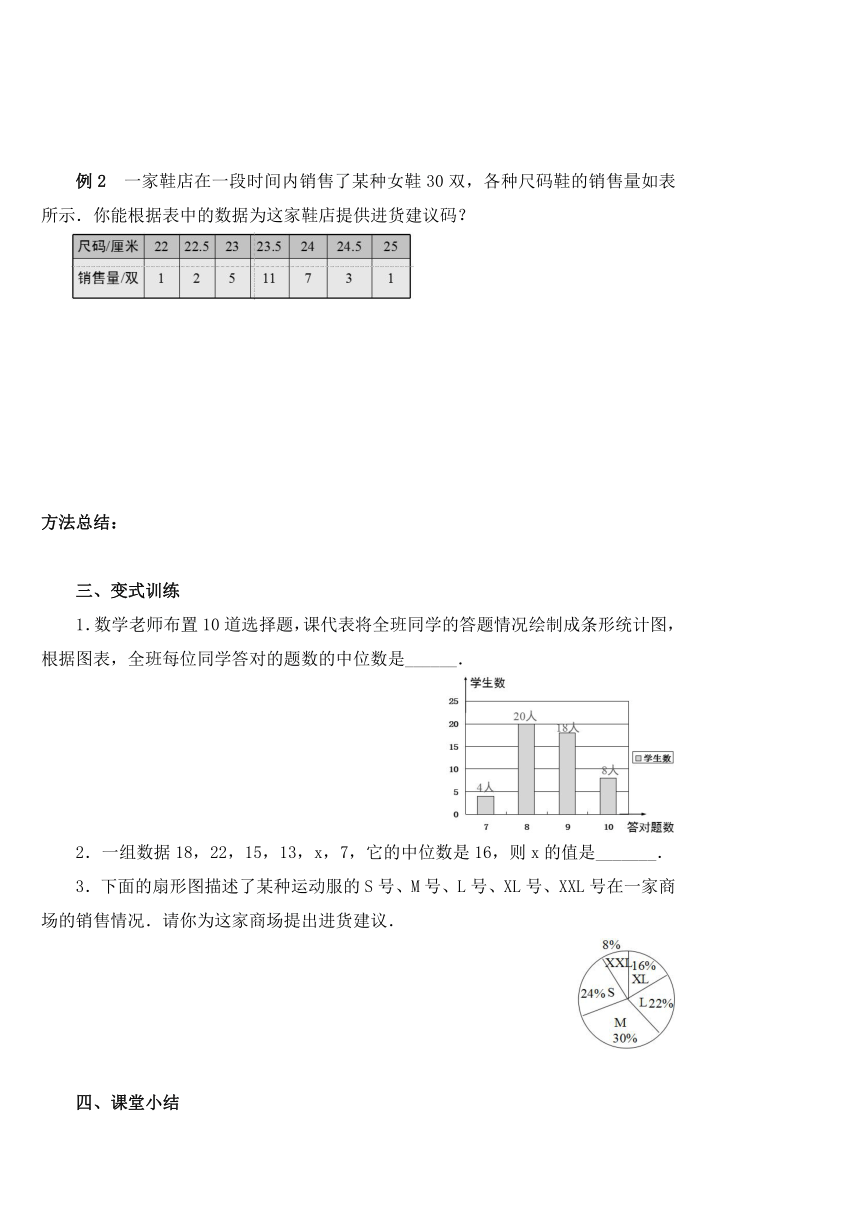
例2 一家鞋店在一段时间内销售了某种女鞋30双,各种尺码鞋的销售量如表所示.你能根据表中的数据为这家鞋店提供进货建议码?
方法总结:
三、变式训练
1.数学老师布置10道选择题,课代表将全班同学的答题情况绘制成条形统计图,根据图表,全班每位同学答对的题数的中位数是______.
2.一组数据18,22,15,13,x,7,它的中位数是16,则x的值是_______.
3.下面的扇形图描述了某种运动服的S号、M号、L号、XL号、XXL号在一家商场的销售情况.请你为这家商场提出进货建议.
四、课堂小结
中位数和众数
中位数 将一组数据按照由小到大(或由大到小)的顺序排列:如果数据的个数是奇数,则称 为这组数据的中位数;如果数据的个数是偶数,则称 为这组数据的中位数.
众数 一组数据中 的数据称为这组数据的众数.
★1.数据1,2,8,5,3,9,5,4,5,4的众数、中位数分别为(?? )
A.4.5,5?? B.5,4.5?? ?? C.5,4??? D.5,5?
★2.在演讲比赛中,你想知道自己在所有选手中处于什么水平,应该选择哪个数据的代表( )
A.平均数?? B.中位数??? C.众数
★3.一组数据1,2,5,x,3,6的众数为5,则这组数据的中位数是_______.
★4.为了了解开展“孝敬父母,从家务事做起”活动的实施情况,某校抽取八年级某班50名学生,调查他们一周做家务所用时间,得到一组数据,并绘制成下表,请根据下表完成各题:
每周做家务的时间(小时) 0 1 1.5 2 2.5 3 3.5 4
人数 2 2 6
12 13 4 3
(1)填写表格中未完成的部分;
(2)该班学生每周做家务的平均时间是 .
(3)这组数据的中位数是 ,众数 .
★★5.两组数据:3,a,2b,5与a,6,b的平均数都是8,若将这两组数据合并为一组数据.
(1)求出a,b的值;
(2)求这组数据的众数和中位数.
★★★6.某校男子足球队的年龄分布如下面的条形图所示.请找出这些队员年龄的平均数、众数、中位数,并解释它们的意义.
我的反思(收获,不足)
分层作业
必做(教材 智慧学习 配套) 选做
参考答案:
自学自测
1.试题分析:根据中位数和众数的定义即可加以判断.
详解:(1)的说法不准确,将一组数据按照由小到大(或由大到小)的顺序排列后,如果数据的个数是奇数,则称中间的一个数为这组数据的中位数;如果数据的个数是偶数,则称 中间两个数的平均数为这组数据的中位数;
(2)是众数的定义,正确;
(3)一组数据的中位数和平均数只有一个,但出现次数最多的数即众数,可以有多个,所以错误;
(4)由于一组数据的中位数一般是将原数据按大小排列后,进行计算得来的,所以中位数不一定是原数据里的数,故(4)错误;
故答案为:(1)×(2)√(3)×(4)×
2.试题分析:本题考查了中位数和众数,将一组数据从小到大((或从大到小))重新排列后,最中间的那个数((或最中间两个数的平均数))叫做这组数据的中位数;众数是一组数据中出现次数最多的数.根据中位数和众数的定义分别进行解答即可.
详解:(1)把这组数据从小到大排列:18,23,27,40,52,90,90,100;
最中间的数是40和52,
则这组数据的中位数是(40+52)=46,
∵90出现了2次,出现的次数最多,则众数是90.
(2)把这组数据从小到大排列:15,21,32,32,32,46,58,64,98.
最中间的数是32,则这组数据的中位数是32;
∵32出现了3次,出现的次数最多,则众数是32.
精讲点拨
例1 试题分析: 由题意可知最中间两位数是10,x,再根据这组数据的中位数与平均数相等,列方程求解即可.
详解:∵数据10,10,x,8(由大到小排列)的中位数与平均数相等,
∴.
解得x=8,=9
∴ 这组数据的中位数为9.
例2 试题分析:商家进货关心的是所销售商品的众数,根据众数的定义即可得解.
详解:由表格可以看出,在女鞋的尺码组成的数据中,23.5是这组数据的众数,即23.5cm的鞋销售量最大.
因此可以建议鞋店多进23.5cm的女鞋.
变式训练
1.试题分析:由条形图可知,全班共有学生4+20+18+8=50人,根据中位数的定义可知,这组数据的中位数是第25、26个数的平均数,计算即可得出答案.
详解:由条形图可知,全班共有学生4+20+18+8=50人,
∵这组数据的第25、26个数均为9,
∴全班答对的题数的中位数是9.
2.试题分析:根据中位数为16和数据的个数,可求出x的值.
详解:由题意得,(15+x)÷2=16,
解得:x=17,
故答案为:17.
3.试题分析:根据扇形图中各型号运动服销售所占的百分比,可以从最大和最小两方面给商家提出进货建议.
详解:由统计图可得:M型号的百分比最大,XXL型号的百分比最小.
所以商场可以多进M型号的运动服,少进XXL型号的运动服.
星级达标:
1.试题分析:根据中位数和众数的定义分别进行解答即可.
详解:把这组数据从小到大排列:1,2,3,4,4,5, 5,5,8,9.
最中间的数是4和5,
则这组数据的中位数是(4+5)=4.5,
∵5出现了3次,出现的次数最多,则众数是5.
故答案为A.
2.试题分析:参赛选手要想知道自己的成绩是处于上游、中游还是下游,应该和中间位置的代表量进行比较,所以应选择中位数.
详解:在演讲比赛中,参赛选手要想知道自己在所有选手中处于什么水平,应该和中间位置的代表量进行比较,所以应选择中位数.
故选答案B.
3.试题分析:先根据众数的概念得出x的值,再将数据重新排列,从而根据中位数的概念可得答案.
详解:∵数据1,2,5,x,3,6的众数为5,
∴,
则数据为1,2,3,5,5,6,
∴这组数据的中位数为,
故答案为4.
4.试题分析:(1)用总人数50减去已知各组的人数,即可得出每周做家务2小时的人数;
(2)算出各组数据的加权平均数即可得解;
(3)根据中位数和众数的定义即可做出判断.
详解:(1)50-2-2-6-12-13-4-3=8,
即表格中的空白处应为8;
(2)该班学生每周做家务的平均时间为:
=2.44(小时)
故答案为2.44.
(3)这组数据的第25、26个数均为2.5,
所以这组数据的中位数是2.5;
数据3出现了13次,出现的次数最多,所以众数为3.
故答案为2.5, 3.
5.试题分析:(1)根据平均数的计算公式可得:,,联立方程组可得:,解方程组可得:,
(2)根据众数是一组数据中出现次数最多,中位数是将一组数据按照大小顺序排列后,最中间的数或最中间两个数的平均数,进行求解.
详解:(1)∵两组数据:3, a,2b,5与a,6,b的平均数都是8,
∴,
解得:,
(2)若将这两组数据合并一组数据,按从小到大的顺序排列为3,5,6,6,12,12,12,
一共7个数,第四个数是6,所以这组数据的中位数是6;
12出现了3次,最多,即众数为12.
6.试题分析:根据条形图所给数据,并结合平均数、中位数及众数的定义即可求解.
详解:这些队员年龄的平均数为:=15(岁),
队员年龄的众数和中位数均为15.
意义:由平均数是15可以说明队员们的平均年龄为15岁;
众数是15可说明队员的年龄为15岁的最多;
中位数是15可说明有一半队员的年龄大于或等于15岁,有一半队员的年龄小于或等于15岁.
第1课时 中位数和众数
学习目标:
1.知道中位数、众数的概念,会求一组数据的中位数、众数.
2.弄清楚中位数、众数的作用,会用中位数、众数分析实际问题.
学习重点:理解中位数、众数的概念,会求一组数据的中位数、众数.
一、课前检测
二、温故知新
1.n个数据a1,a2,a3,a4,…,an的算术平均数 .
2.若n个数x1,x2,…,xn的权分别是w1,w2,…,wn,则__________________叫做这n个数的加权平均数.
3.n个数据:f1个a1,f2个a2,…,fn个an,它的加权平均数为 .
三、预习导航(预习教材第116-118页,标出你认为重要的关键词)
1.下表是某公司员工月收入的资料.
(1)计算这个公司员工月收入的平均数;
(2)如果用(1)算得的平均数反映公司全体员工月收入水平,你认为合适吗?
(3)该公司员工的中等收入水平大概是多少元?你是怎样确定的?
(4)“平均数”和“中等水平”谁更合理地反映了该公司绝大部分员工的月工资水平?这个问题中,中等水平的含义是什么?
2.自主归纳:
(1)将一组数据按照由小到大(或由大到小)的顺序排列:
如果数据的个数是奇数,则称 为这组数据的中位数;
如果数据的个数是偶数,则称 为这组数据的中位数.
(2)一组数据中 的数据称为这组数据的众数.
四、自学自测
1.判断:
(1)一组数据中间的数称为中位数. ( )
(2)一组数据中出现次数最多的数称为这组数据的众数.( )
(3)一组数据中的中位数和众数是唯一的一个数. ( )
(4)一组数据的中位数一定是这组数据中的某个数. ( )
2.求出下面各组数据的中位数和众数:
(1)90,23,27,40,90,18,52,100;
(2)21,15,32,32,46,32,58,64,98.
五、我的疑惑(反思)
__________________________________________________________________________________________________________________________________________________
要点探究
探究点1:中位数
问题1:确定一组数据的中位数时,要注意什么?
问题2:中位数反映的是一组数据的何种特征,它有何意义?
即学即练 在一次男子马拉松长跑比赛中,抽得12名选手所用时间(单位:min)如下:
136 140 129 180 124 154
146 145 158 175 165 148
(1)样本数据(12名选手的成绩)的中位数是多少?
(2)一名选手的成绩是142min,他的成绩如何?
要点提醒:
1.中位数是一个位置代表值(中间数),它是唯一的,且不一定出现在这组数据中.
2.中位数仅与数据的排列位置有关,如果一组数据中有极端数据时,中位数能比平均数更能合理地反映该组数据的整体水平.
3.如果已知一组数据的中位数,那么中位数以上和以下的数据个数相等.
探究点2:众数
问题3:如果小张是该公司的一名普通员工,那么你认为他的月工资最有可能是多少元?
问题4:一组数据的众数一定是唯一的吗?请举例说明.
要点提醒:
1.一组数据的众数可能不止一个,但一定是这组数据的某一个或几个数.
2.一组数据中,若每个数据出现的频数相同,则这组数据没有众数.
二、精讲点拨
例1 已知一组数据10,10,x,8(由大到小排列)的中位数与平均数相等,求x值及这组数据的中位数.
分析:由题意可知最中间两位数是10,x,列方程求解即可.
例2 一家鞋店在一段时间内销售了某种女鞋30双,各种尺码鞋的销售量如表所示.你能根据表中的数据为这家鞋店提供进货建议码?
方法总结:
三、变式训练
1.数学老师布置10道选择题,课代表将全班同学的答题情况绘制成条形统计图,根据图表,全班每位同学答对的题数的中位数是______.
2.一组数据18,22,15,13,x,7,它的中位数是16,则x的值是_______.
3.下面的扇形图描述了某种运动服的S号、M号、L号、XL号、XXL号在一家商场的销售情况.请你为这家商场提出进货建议.
四、课堂小结
中位数和众数
中位数 将一组数据按照由小到大(或由大到小)的顺序排列:如果数据的个数是奇数,则称 为这组数据的中位数;如果数据的个数是偶数,则称 为这组数据的中位数.
众数 一组数据中 的数据称为这组数据的众数.
★1.数据1,2,8,5,3,9,5,4,5,4的众数、中位数分别为(?? )
A.4.5,5?? B.5,4.5?? ?? C.5,4??? D.5,5?
★2.在演讲比赛中,你想知道自己在所有选手中处于什么水平,应该选择哪个数据的代表( )
A.平均数?? B.中位数??? C.众数
★3.一组数据1,2,5,x,3,6的众数为5,则这组数据的中位数是_______.
★4.为了了解开展“孝敬父母,从家务事做起”活动的实施情况,某校抽取八年级某班50名学生,调查他们一周做家务所用时间,得到一组数据,并绘制成下表,请根据下表完成各题:
每周做家务的时间(小时) 0 1 1.5 2 2.5 3 3.5 4
人数 2 2 6
12 13 4 3
(1)填写表格中未完成的部分;
(2)该班学生每周做家务的平均时间是 .
(3)这组数据的中位数是 ,众数 .
★★5.两组数据:3,a,2b,5与a,6,b的平均数都是8,若将这两组数据合并为一组数据.
(1)求出a,b的值;
(2)求这组数据的众数和中位数.
★★★6.某校男子足球队的年龄分布如下面的条形图所示.请找出这些队员年龄的平均数、众数、中位数,并解释它们的意义.
我的反思(收获,不足)
分层作业
必做(教材 智慧学习 配套) 选做
参考答案:
自学自测
1.试题分析:根据中位数和众数的定义即可加以判断.
详解:(1)的说法不准确,将一组数据按照由小到大(或由大到小)的顺序排列后,如果数据的个数是奇数,则称中间的一个数为这组数据的中位数;如果数据的个数是偶数,则称 中间两个数的平均数为这组数据的中位数;
(2)是众数的定义,正确;
(3)一组数据的中位数和平均数只有一个,但出现次数最多的数即众数,可以有多个,所以错误;
(4)由于一组数据的中位数一般是将原数据按大小排列后,进行计算得来的,所以中位数不一定是原数据里的数,故(4)错误;
故答案为:(1)×(2)√(3)×(4)×
2.试题分析:本题考查了中位数和众数,将一组数据从小到大((或从大到小))重新排列后,最中间的那个数((或最中间两个数的平均数))叫做这组数据的中位数;众数是一组数据中出现次数最多的数.根据中位数和众数的定义分别进行解答即可.
详解:(1)把这组数据从小到大排列:18,23,27,40,52,90,90,100;
最中间的数是40和52,
则这组数据的中位数是(40+52)=46,
∵90出现了2次,出现的次数最多,则众数是90.
(2)把这组数据从小到大排列:15,21,32,32,32,46,58,64,98.
最中间的数是32,则这组数据的中位数是32;
∵32出现了3次,出现的次数最多,则众数是32.
精讲点拨
例1 试题分析: 由题意可知最中间两位数是10,x,再根据这组数据的中位数与平均数相等,列方程求解即可.
详解:∵数据10,10,x,8(由大到小排列)的中位数与平均数相等,
∴.
解得x=8,=9
∴ 这组数据的中位数为9.
例2 试题分析:商家进货关心的是所销售商品的众数,根据众数的定义即可得解.
详解:由表格可以看出,在女鞋的尺码组成的数据中,23.5是这组数据的众数,即23.5cm的鞋销售量最大.
因此可以建议鞋店多进23.5cm的女鞋.
变式训练
1.试题分析:由条形图可知,全班共有学生4+20+18+8=50人,根据中位数的定义可知,这组数据的中位数是第25、26个数的平均数,计算即可得出答案.
详解:由条形图可知,全班共有学生4+20+18+8=50人,
∵这组数据的第25、26个数均为9,
∴全班答对的题数的中位数是9.
2.试题分析:根据中位数为16和数据的个数,可求出x的值.
详解:由题意得,(15+x)÷2=16,
解得:x=17,
故答案为:17.
3.试题分析:根据扇形图中各型号运动服销售所占的百分比,可以从最大和最小两方面给商家提出进货建议.
详解:由统计图可得:M型号的百分比最大,XXL型号的百分比最小.
所以商场可以多进M型号的运动服,少进XXL型号的运动服.
星级达标:
1.试题分析:根据中位数和众数的定义分别进行解答即可.
详解:把这组数据从小到大排列:1,2,3,4,4,5, 5,5,8,9.
最中间的数是4和5,
则这组数据的中位数是(4+5)=4.5,
∵5出现了3次,出现的次数最多,则众数是5.
故答案为A.
2.试题分析:参赛选手要想知道自己的成绩是处于上游、中游还是下游,应该和中间位置的代表量进行比较,所以应选择中位数.
详解:在演讲比赛中,参赛选手要想知道自己在所有选手中处于什么水平,应该和中间位置的代表量进行比较,所以应选择中位数.
故选答案B.
3.试题分析:先根据众数的概念得出x的值,再将数据重新排列,从而根据中位数的概念可得答案.
详解:∵数据1,2,5,x,3,6的众数为5,
∴,
则数据为1,2,3,5,5,6,
∴这组数据的中位数为,
故答案为4.
4.试题分析:(1)用总人数50减去已知各组的人数,即可得出每周做家务2小时的人数;
(2)算出各组数据的加权平均数即可得解;
(3)根据中位数和众数的定义即可做出判断.
详解:(1)50-2-2-6-12-13-4-3=8,
即表格中的空白处应为8;
(2)该班学生每周做家务的平均时间为:
=2.44(小时)
故答案为2.44.
(3)这组数据的第25、26个数均为2.5,
所以这组数据的中位数是2.5;
数据3出现了13次,出现的次数最多,所以众数为3.
故答案为2.5, 3.
5.试题分析:(1)根据平均数的计算公式可得:,,联立方程组可得:,解方程组可得:,
(2)根据众数是一组数据中出现次数最多,中位数是将一组数据按照大小顺序排列后,最中间的数或最中间两个数的平均数,进行求解.
详解:(1)∵两组数据:3, a,2b,5与a,6,b的平均数都是8,
∴,
解得:,
(2)若将这两组数据合并一组数据,按从小到大的顺序排列为3,5,6,6,12,12,12,
一共7个数,第四个数是6,所以这组数据的中位数是6;
12出现了3次,最多,即众数为12.
6.试题分析:根据条形图所给数据,并结合平均数、中位数及众数的定义即可求解.
详解:这些队员年龄的平均数为:=15(岁),
队员年龄的众数和中位数均为15.
意义:由平均数是15可以说明队员们的平均年龄为15岁;
众数是15可说明队员的年龄为15岁的最多;
中位数是15可说明有一半队员的年龄大于或等于15岁,有一半队员的年龄小于或等于15岁.
