第18章平行四边形复习-2020-2021学年人教版八年级数学下册导学案(含详解)
文档属性
| 名称 | 第18章平行四边形复习-2020-2021学年人教版八年级数学下册导学案(含详解) |  | |
| 格式 | docx | ||
| 文件大小 | 544.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-31 15:16:56 | ||
图片预览



文档简介
-1591945-123825第十八章 平行四边形复习
学习目标:
1.通过对本章知识的回顾,对比掌握各种特殊四边形的概念、性质和判定方法.
2.归纳总结常用添加辅助线的方法.
学习重点:平行四边形与特殊平行四边形的从属关系,以及它们的概念、性质和判定方法.
自主研习
自主研习
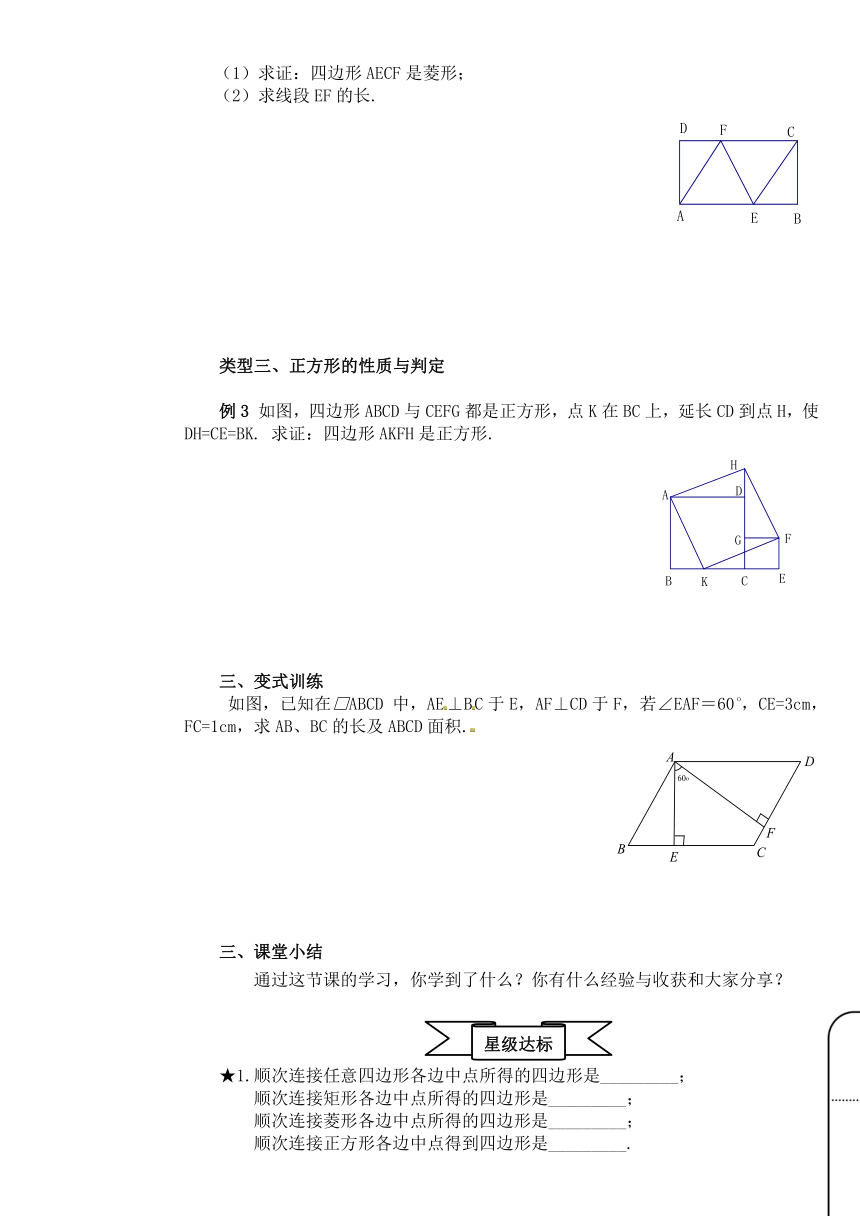
一、课前检测
温故知新
1600200580263014478005650230
1295400549783011430005345430三、独立画出本章知识结构图
四、我的疑惑(反思)
探究点拨
探究点拨
要点回顾
二、精讲点拨
类型一、平行四边形的性质与判定
例1 如图,ABCD为平行四边形,E、F分别为AB、CD的中点.
①求证:AECF也是平行四边形;②连接BD,分别交CE、AF于G、H,求证:BG=DH;③连接CH、AG,则AGCH是平行四边形吗?说明理由.
类型二、矩形、菱形的性质与判定
例2 如图,在矩形ABCD中,AB=4,BC=2,点E,F分别在AB,CD上,且BE=DF=false.
求证:四边形AECF是菱形;
求线段EF的长.
类型三、正方形的性质与判定
例3 如图,四边形ABCD与CEFG都是正方形,点K在BC上,延长CD到点H,使DH=CE=BK. 求证:四边形AKFH是正方形.
三、变式训练
如图,已知在□ABCD 中,AE⊥BC于E,AF⊥CD于F,若∠EAF=60 o,CE=3cm,FC=1cm,求AB、BC的长及ABCD面积.
课堂小结
通过这节课的学习,你学到了什么?你有什么经验与收获和大家分享?
5599430-92075星级达标
星级达标
★1.顺次连接任意四边形各边中点所得的四边形是_________;
顺次连接矩形各边中点所得的四边形是_________;
顺次连接菱形各边中点所得的四边形是_________;
顺次连接正方形各边中点得到四边形是_________.
3733165443865★★2.如图,在□ABCD中,CD=2AD,BE⊥AD于点E,F为DC的中点,连接EF,BF,下列结论:①∠ABC=2∠ABF;②EF=BF;③S四边形DEBC=2S△EFB;④∠CFE=3∠DEF.其中正确结论的个数共有( )
A.1个 B.2个 C.3个 D.4个
★★3.□ABCD的内角∠BCD的平分线CE交AD于点E,若CE分AD为3和4两部分,试求□ABCD的周长.
★★4.如图,△ABC中,D是BC上任意一点,DE∥AC,DF∥AB.
(1)试判断四边形AEDF的形状,并说明理由.
(2)连接AD,当AD满足什么条件时,四边形AEDF为菱形,为什么?
(3)在(2)的条件下,当△ABC满足什么条件时,四边形AEDF为正方形,不说明理由.
436118013335
★★★5.如图,矩形ABCD中的长AB=8false,宽AD=6false,沿过BD的中点O的直线对折,使B与D点重合,求证:四边形BEDF为菱形,并求折痕EF的长.
我的反思(收获,不足)
分层作业
必做(教材 智慧学习 配套) 选做
参考答案:
例1 试题分析:(1)由平行四边形的性质得出AB∥CD,AB=CD,根据E、F分别为AB、CD的中点,证出AE=CF,即可得出四边形AECF也是平行四边形;
(2)由AAS证明△ADH≌△CBG,即可得出结论;
(3)连接CA交BD于O,由平行四边形的性质得出OA=OC,OB=OD,证出OH=OG,即可得出四边形AGCH也是平行四边形.
(1)证明:∵四边形ABCD是平行四边形,
∴AB∥CD,AD∥BC,AB=CD,AD=CB.
∵E、F分别为AB、CD的中点,
2964180233680∴AE=CF,
∴四边形AECF是平行四边形.
(2)证明:∵AD∥BC,
∴∠ADH=∠CBG,
∵四边形AECF也是平行四边形,
∴∠CGB=∠FHB.
∵∠FHB=∠AHD,
∴∠AHD=∠CGB.
在△ADH和△CBG中,
,
∴ADH≌△CBG(AAS), ∴DH=BG.
(3)解:四边形AGCH也是平行四边形;理由如下:
连接CA交BD于O,如图所示:
∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD,
∵DH=BG,∴OH=OG,
∴四边形AGCH也是平行四边形.
例2 试题分析:本题考查了矩形的性质,菱形的判定和性质,勾股定理等知识.(1)根据矩形的性质得到CD=AB=4,AD=BC=2,CD∥AB,∠D=∠B=90°,求得CF=AE=4﹣=,根据勾股定理得到AF=CE==,于是得到结论;
(2)过F作FH⊥AB于H,得到四边形AHFD是矩形,根据矩形的性质得到AH=DF=,FH=AD=2,根据勾股定理即可得到结论.
(1)证明:∵在矩形ABCD中,AB=4,BC=2,
∴CD=AB=4,AD=BC=2,CD∥AB,∠D=∠B=90°,
3564255287655∵BE=DF=,
∴CF=AE=4﹣=,
∴AF=CE==,
∴AF=CF=CE=AE=,
∴四边形AECF是菱形;
(2)解:过F作FH⊥AB于H,则四边形AHFD是矩形.
∴AH=DF=,FH=AD=2,
∴EH=﹣=1,
在Rt△EFH中,EF===.
例3 试题分析:利用正方形的性质结合全等三角形的判定方法得出:△HGF≌△KEF≌△ABK≌△ADH,再利用正方形的判定方法得出答案.
证明:∵四边形ABCD和CEFG都是正方形,
3652520236220∴AB=AD=DC=BC,GC=EC=FG=EF.
∠ABC=∠ADC=∠ADH=90°.
∵DH=CE=BK,
∴HG=EK=BC=AD=AB.
在△ADH和△ABK中,
,
∴△ADH≌△ABK(SAS).
∴∠HAD=∠BAK.
∴∠HAK=90°.
同理可得:△HGF≌△KEF≌△ABK≌△ADH.
∴AH=AK=HF=FK,
∴四边形AKFH是正方形.
变式训练
试题分析:根据AE⊥BC于E,AF⊥CD于F,∠EAF=60°,可以得到∠C的度数,由四边形ABCD是平行四边形可以得到∠B、∠D的度数,然后根据30°角所对的直角边和斜边的关系,可以求得AB、BC的长,根据勾股定理求得AE的长,由平行四边形的面积公式求得四边形ABCD的面积.
详解:∵AE⊥BC,AF⊥CD,∠EAF=60°,
336994588900∴∠AEC=∠AFC=90°,
∴∠C=360°﹣∠AEC﹣∠EAF﹣∠AFC=120°,
∵四边形ABCD是平行四边形,
∴∠C+∠B=180°,
∴∠B=∠D=60°,∴∠BAE=∠DAF=30°.
∴AB=2BE,AD=2DF.
设BE=a,则AB=2a,
∵CE=3cm,FC=1cm,
∴DF=2a﹣1,
∵∠DAF=30°,∴AD=2DF=4a﹣2.
∵AD=BC,即4a-2=a+3. 解得a=.
∴AB=2a=,BC=a+3=,
在Rt△ABE中,AE=false=AB.
∴平行四边形ABCD的面积是:BC?AE=,
即AB的长是cm,BC的长是cm,平行四边形ABCD的面积是.
星级达标:
1.试题分析:根据三角形的中位线定理可证明:顺次连接四边形的各边中点所得四边形是平行四边形;顺次连接对角线相等的四边形各边中点所得四边形是菱形;顺次连接对角线互相垂直的四边形各边中点所得四边形是矩形.根据上述结论进行判断即可.
详解:顺次连接四边形的各边中点所得四边形是平行四边形;
矩形的对角线相等,所以顺次连接矩形各边中点所得四边形是菱形;
菱形的对角线互相垂直,所以顺次连接菱形各边中点所得四边形的是矩形;
正方形的对角线相等且垂直,所以顺次连接正方形各边中点的四边形既是矩形又是菱形,是正方形.
故答案分别为平行四边形;菱形;矩形;正方形.
2.试题分析:本题考查平行四边形的性质和判定、菱形的判定和性质、直角三角形斜边中线的性质、全等三角形的判定和性质等知识,解题的关键是学会添加常用辅助线,构造全等三角形解决问题.如图延长EF交BC的延长线于G,取AB的中点H连接FH.通过全等证明EF=FG,进而可得BE⊥BG,四边形BCFH是菱形即可解决问题.
详解:如图延长EF交BC的延长线于G,取AB的中点H连接FH.
4497705274320∵CD=2AD,DF=FC,
∴CF=CB,∴∠CFB=∠CBF.
∵CD∥AB,∴∠CFB=∠FBH.
∴∠CBF=∠FBH,
∴∠ABC=2∠ABF.故①正确;
∵DE∥CG,∴∠D=∠FCG.
∵DF=FC,∠DFE=∠CFG,
∴△DFE≌△CFG(ASA),∴FE=FG.
∵BE⊥AD,∴∠AEB=90°.
∵AD∥BC,∴∠AEB=∠EBG=90°.
∴BF=EF=FG,故②正确;
∵S△DFE=S△CFG,
∴S四边形DEBC=S△EBG=2S△BEF,故③正确;
∵AH=HB,DF=CF,AB=CD,
∴CF=BH,∵CF∥BH,
∴四边形BCFH是平行四边形,
∵CF=BC, ∴四边形BCFH是菱形.
∴∠BFC=∠BFH,
∵FE=FB,FH∥AD,BE⊥AD,
∴FH⊥BE,
∴∠BFH=∠EFH=∠DEF,
∴∠EFC=3∠DEF,故④正确. 故选答案D.
试题分析:本题用到了一个基本模型“平行线+角平分线=等腰三角形”,CE分AD为3和4两部分,有两种可能,AE=3,DE=4或AE=4,DE=3,再根据平行四边形的周长公式进行计算即可.
详解:在□ABCD中,AB=CD,AD=BC,AD∥BC.
∴∠BCE=∠DEC.
∵CE平分∠BCD,∴∠BCE=∠DCE.
∴∠DEC=∠DCE.∴DE=CD.
∵CE分AD为3和4两部分,
∴当AE=3,DE=4时,AD=AE+DE=3+4=7,CD=DE=4.
∴□ABCD的周长=2AD+2CD=2×7+2×4=22.
当AE=4,DE=3时,AD=AE+DE=4+3=7,CD=DE=3.
∴□ABCD的周长=2AD+2CD=2×7+2×3=20.
故□ABCD的周长为22或20.
4.试题分析:①根据DE∥AC,DF∥AB可判断四边形AEDF为平行四边形;
②由四边形AEDF为菱形,能得出AD为∠BAC的平分线即可;
③由四边形AEDF为正方形,得∠BAC=90°,即当△ABC是以BC为斜边的直角三角形即可.
详解:①四边形AEDF是平行四边形.理由如下:
∵DE∥AC,DF∥AB,
∴四边形AEDF为平行四边形.
②当AD平分∠BAC时,四边形AEDF为菱形.理由如下:
∵AD平分∠BAC,∴∠BAD=∠CAD.
∵DF∥AB,∴∠ADE=∠CAD.
∴∠ADE=∠EAD.∴AE=DE.
∴四边形AEDF为菱形.
③当△ABC是以BC为斜边的直角三角形,四边形AEDF为正方形,理由如下:
∵△ABC是以BC为斜边的直角三角形,∴∠BAC=90°.
∴菱形AEDF为正方形.
5.试题分析:本题考查了菱形的判定及勾股定理,根据平行四边形的对角线互相垂直即可判定;在求EF的长时,对角线BD是可求的,设BE的长为x,利用勾股定理求出BE,OE即可.
证明:∵纸片沿过BD的中点O的直线对折、使B与D点重合,
∴EF⊥BD,OD=OB,∠DOE=∠BOF,
346900545720∵AB∥CD,
∴∠ODE=∠OBF,
∴△DOE≌△BOF,所以DE=BF,
∵DE∥BF,
∴四边形BEDF是平行四边形,
∵EF⊥BD,
∴四边形BEDF为菱形;
连接BE,由题意可得:EF垂直平分BD,
所以BE=DE,又OB=BD==5,
设BE=ED=x,则CE=8﹣x,
在Rt△BCE中,由勾股定理可得:x2=(8﹣x)2+62,解得x=,
又在Rt△ODE中,由勾股定理可得:OE==,
而△DOE≌△BOF,所以OE=OF,故EF=false(cm).
学习目标:
1.通过对本章知识的回顾,对比掌握各种特殊四边形的概念、性质和判定方法.
2.归纳总结常用添加辅助线的方法.
学习重点:平行四边形与特殊平行四边形的从属关系,以及它们的概念、性质和判定方法.
自主研习
自主研习
一、课前检测
温故知新
1600200580263014478005650230
1295400549783011430005345430三、独立画出本章知识结构图
四、我的疑惑(反思)
探究点拨
探究点拨
要点回顾
二、精讲点拨
类型一、平行四边形的性质与判定
例1 如图,ABCD为平行四边形,E、F分别为AB、CD的中点.
①求证:AECF也是平行四边形;②连接BD,分别交CE、AF于G、H,求证:BG=DH;③连接CH、AG,则AGCH是平行四边形吗?说明理由.
类型二、矩形、菱形的性质与判定
例2 如图,在矩形ABCD中,AB=4,BC=2,点E,F分别在AB,CD上,且BE=DF=false.
求证:四边形AECF是菱形;
求线段EF的长.
类型三、正方形的性质与判定
例3 如图,四边形ABCD与CEFG都是正方形,点K在BC上,延长CD到点H,使DH=CE=BK. 求证:四边形AKFH是正方形.
三、变式训练
如图,已知在□ABCD 中,AE⊥BC于E,AF⊥CD于F,若∠EAF=60 o,CE=3cm,FC=1cm,求AB、BC的长及ABCD面积.
课堂小结
通过这节课的学习,你学到了什么?你有什么经验与收获和大家分享?
5599430-92075星级达标
星级达标
★1.顺次连接任意四边形各边中点所得的四边形是_________;
顺次连接矩形各边中点所得的四边形是_________;
顺次连接菱形各边中点所得的四边形是_________;
顺次连接正方形各边中点得到四边形是_________.
3733165443865★★2.如图,在□ABCD中,CD=2AD,BE⊥AD于点E,F为DC的中点,连接EF,BF,下列结论:①∠ABC=2∠ABF;②EF=BF;③S四边形DEBC=2S△EFB;④∠CFE=3∠DEF.其中正确结论的个数共有( )
A.1个 B.2个 C.3个 D.4个
★★3.□ABCD的内角∠BCD的平分线CE交AD于点E,若CE分AD为3和4两部分,试求□ABCD的周长.
★★4.如图,△ABC中,D是BC上任意一点,DE∥AC,DF∥AB.
(1)试判断四边形AEDF的形状,并说明理由.
(2)连接AD,当AD满足什么条件时,四边形AEDF为菱形,为什么?
(3)在(2)的条件下,当△ABC满足什么条件时,四边形AEDF为正方形,不说明理由.
436118013335
★★★5.如图,矩形ABCD中的长AB=8false,宽AD=6false,沿过BD的中点O的直线对折,使B与D点重合,求证:四边形BEDF为菱形,并求折痕EF的长.
我的反思(收获,不足)
分层作业
必做(教材 智慧学习 配套) 选做
参考答案:
例1 试题分析:(1)由平行四边形的性质得出AB∥CD,AB=CD,根据E、F分别为AB、CD的中点,证出AE=CF,即可得出四边形AECF也是平行四边形;
(2)由AAS证明△ADH≌△CBG,即可得出结论;
(3)连接CA交BD于O,由平行四边形的性质得出OA=OC,OB=OD,证出OH=OG,即可得出四边形AGCH也是平行四边形.
(1)证明:∵四边形ABCD是平行四边形,
∴AB∥CD,AD∥BC,AB=CD,AD=CB.
∵E、F分别为AB、CD的中点,
2964180233680∴AE=CF,
∴四边形AECF是平行四边形.
(2)证明:∵AD∥BC,
∴∠ADH=∠CBG,
∵四边形AECF也是平行四边形,
∴∠CGB=∠FHB.
∵∠FHB=∠AHD,
∴∠AHD=∠CGB.
在△ADH和△CBG中,
,
∴ADH≌△CBG(AAS), ∴DH=BG.
(3)解:四边形AGCH也是平行四边形;理由如下:
连接CA交BD于O,如图所示:
∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD,
∵DH=BG,∴OH=OG,
∴四边形AGCH也是平行四边形.
例2 试题分析:本题考查了矩形的性质,菱形的判定和性质,勾股定理等知识.(1)根据矩形的性质得到CD=AB=4,AD=BC=2,CD∥AB,∠D=∠B=90°,求得CF=AE=4﹣=,根据勾股定理得到AF=CE==,于是得到结论;
(2)过F作FH⊥AB于H,得到四边形AHFD是矩形,根据矩形的性质得到AH=DF=,FH=AD=2,根据勾股定理即可得到结论.
(1)证明:∵在矩形ABCD中,AB=4,BC=2,
∴CD=AB=4,AD=BC=2,CD∥AB,∠D=∠B=90°,
3564255287655∵BE=DF=,
∴CF=AE=4﹣=,
∴AF=CE==,
∴AF=CF=CE=AE=,
∴四边形AECF是菱形;
(2)解:过F作FH⊥AB于H,则四边形AHFD是矩形.
∴AH=DF=,FH=AD=2,
∴EH=﹣=1,
在Rt△EFH中,EF===.
例3 试题分析:利用正方形的性质结合全等三角形的判定方法得出:△HGF≌△KEF≌△ABK≌△ADH,再利用正方形的判定方法得出答案.
证明:∵四边形ABCD和CEFG都是正方形,
3652520236220∴AB=AD=DC=BC,GC=EC=FG=EF.
∠ABC=∠ADC=∠ADH=90°.
∵DH=CE=BK,
∴HG=EK=BC=AD=AB.
在△ADH和△ABK中,
,
∴△ADH≌△ABK(SAS).
∴∠HAD=∠BAK.
∴∠HAK=90°.
同理可得:△HGF≌△KEF≌△ABK≌△ADH.
∴AH=AK=HF=FK,
∴四边形AKFH是正方形.
变式训练
试题分析:根据AE⊥BC于E,AF⊥CD于F,∠EAF=60°,可以得到∠C的度数,由四边形ABCD是平行四边形可以得到∠B、∠D的度数,然后根据30°角所对的直角边和斜边的关系,可以求得AB、BC的长,根据勾股定理求得AE的长,由平行四边形的面积公式求得四边形ABCD的面积.
详解:∵AE⊥BC,AF⊥CD,∠EAF=60°,
336994588900∴∠AEC=∠AFC=90°,
∴∠C=360°﹣∠AEC﹣∠EAF﹣∠AFC=120°,
∵四边形ABCD是平行四边形,
∴∠C+∠B=180°,
∴∠B=∠D=60°,∴∠BAE=∠DAF=30°.
∴AB=2BE,AD=2DF.
设BE=a,则AB=2a,
∵CE=3cm,FC=1cm,
∴DF=2a﹣1,
∵∠DAF=30°,∴AD=2DF=4a﹣2.
∵AD=BC,即4a-2=a+3. 解得a=.
∴AB=2a=,BC=a+3=,
在Rt△ABE中,AE=false=AB.
∴平行四边形ABCD的面积是:BC?AE=,
即AB的长是cm,BC的长是cm,平行四边形ABCD的面积是.
星级达标:
1.试题分析:根据三角形的中位线定理可证明:顺次连接四边形的各边中点所得四边形是平行四边形;顺次连接对角线相等的四边形各边中点所得四边形是菱形;顺次连接对角线互相垂直的四边形各边中点所得四边形是矩形.根据上述结论进行判断即可.
详解:顺次连接四边形的各边中点所得四边形是平行四边形;
矩形的对角线相等,所以顺次连接矩形各边中点所得四边形是菱形;
菱形的对角线互相垂直,所以顺次连接菱形各边中点所得四边形的是矩形;
正方形的对角线相等且垂直,所以顺次连接正方形各边中点的四边形既是矩形又是菱形,是正方形.
故答案分别为平行四边形;菱形;矩形;正方形.
2.试题分析:本题考查平行四边形的性质和判定、菱形的判定和性质、直角三角形斜边中线的性质、全等三角形的判定和性质等知识,解题的关键是学会添加常用辅助线,构造全等三角形解决问题.如图延长EF交BC的延长线于G,取AB的中点H连接FH.通过全等证明EF=FG,进而可得BE⊥BG,四边形BCFH是菱形即可解决问题.
详解:如图延长EF交BC的延长线于G,取AB的中点H连接FH.
4497705274320∵CD=2AD,DF=FC,
∴CF=CB,∴∠CFB=∠CBF.
∵CD∥AB,∴∠CFB=∠FBH.
∴∠CBF=∠FBH,
∴∠ABC=2∠ABF.故①正确;
∵DE∥CG,∴∠D=∠FCG.
∵DF=FC,∠DFE=∠CFG,
∴△DFE≌△CFG(ASA),∴FE=FG.
∵BE⊥AD,∴∠AEB=90°.
∵AD∥BC,∴∠AEB=∠EBG=90°.
∴BF=EF=FG,故②正确;
∵S△DFE=S△CFG,
∴S四边形DEBC=S△EBG=2S△BEF,故③正确;
∵AH=HB,DF=CF,AB=CD,
∴CF=BH,∵CF∥BH,
∴四边形BCFH是平行四边形,
∵CF=BC, ∴四边形BCFH是菱形.
∴∠BFC=∠BFH,
∵FE=FB,FH∥AD,BE⊥AD,
∴FH⊥BE,
∴∠BFH=∠EFH=∠DEF,
∴∠EFC=3∠DEF,故④正确. 故选答案D.
试题分析:本题用到了一个基本模型“平行线+角平分线=等腰三角形”,CE分AD为3和4两部分,有两种可能,AE=3,DE=4或AE=4,DE=3,再根据平行四边形的周长公式进行计算即可.
详解:在□ABCD中,AB=CD,AD=BC,AD∥BC.
∴∠BCE=∠DEC.
∵CE平分∠BCD,∴∠BCE=∠DCE.
∴∠DEC=∠DCE.∴DE=CD.
∵CE分AD为3和4两部分,
∴当AE=3,DE=4时,AD=AE+DE=3+4=7,CD=DE=4.
∴□ABCD的周长=2AD+2CD=2×7+2×4=22.
当AE=4,DE=3时,AD=AE+DE=4+3=7,CD=DE=3.
∴□ABCD的周长=2AD+2CD=2×7+2×3=20.
故□ABCD的周长为22或20.
4.试题分析:①根据DE∥AC,DF∥AB可判断四边形AEDF为平行四边形;
②由四边形AEDF为菱形,能得出AD为∠BAC的平分线即可;
③由四边形AEDF为正方形,得∠BAC=90°,即当△ABC是以BC为斜边的直角三角形即可.
详解:①四边形AEDF是平行四边形.理由如下:
∵DE∥AC,DF∥AB,
∴四边形AEDF为平行四边形.
②当AD平分∠BAC时,四边形AEDF为菱形.理由如下:
∵AD平分∠BAC,∴∠BAD=∠CAD.
∵DF∥AB,∴∠ADE=∠CAD.
∴∠ADE=∠EAD.∴AE=DE.
∴四边形AEDF为菱形.
③当△ABC是以BC为斜边的直角三角形,四边形AEDF为正方形,理由如下:
∵△ABC是以BC为斜边的直角三角形,∴∠BAC=90°.
∴菱形AEDF为正方形.
5.试题分析:本题考查了菱形的判定及勾股定理,根据平行四边形的对角线互相垂直即可判定;在求EF的长时,对角线BD是可求的,设BE的长为x,利用勾股定理求出BE,OE即可.
证明:∵纸片沿过BD的中点O的直线对折、使B与D点重合,
∴EF⊥BD,OD=OB,∠DOE=∠BOF,
346900545720∵AB∥CD,
∴∠ODE=∠OBF,
∴△DOE≌△BOF,所以DE=BF,
∵DE∥BF,
∴四边形BEDF是平行四边形,
∵EF⊥BD,
∴四边形BEDF为菱形;
连接BE,由题意可得:EF垂直平分BD,
所以BE=DE,又OB=BD==5,
设BE=ED=x,则CE=8﹣x,
在Rt△BCE中,由勾股定理可得:x2=(8﹣x)2+62,解得x=,
又在Rt△ODE中,由勾股定理可得:OE==,
而△DOE≌△BOF,所以OE=OF,故EF=false(cm).
