19.1.2函数的图象(第1课时)-2020-2021学年人教版八年级数学下册导学案(含详解)
文档属性
| 名称 | 19.1.2函数的图象(第1课时)-2020-2021学年人教版八年级数学下册导学案(含详解) |

|
|
| 格式 | doc | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-31 15:18:32 | ||
图片预览

文档简介
19.1.2 函数的图象
第1课时 函数的图象
1.知道函数的图象的概念.
2.掌握画函数图象的一般步骤,能画出一些简单的函数图象.
3.能根据所给函数图象读出一些有用的信息.
学习重点:函数图象的意义及画法.
一、课前检测
一辆汽车的油箱中现有汽油50L,如果不再加油,那么油箱中的油量y(单位:L)随行驶里程x(单位:千米)的增加而减少,平均耗油量为0.1L/千米.
(1)写出表示y与x的函数关系式.
(2)指出自变量x的取值范围.
(3) 汽车行驶200千米时,油箱中还有多少汽油?
二、温故知新
在平面直角坐标系中,平面内的点可以用一对 来表示.即坐标平面内的 与有序数对是一一 的.
三、预习导航(预习教材第75-79页,标出你认为重要的关键词)
1.(1)正方形的面积S与边长x的函数解析式为 ,其中自变量x的取值范围是 .
(2)根据S与x的函数解析式填写下表:
x 0.5 1 1.5 2 2.5 3 3.5
S
(3)根据S与x的每组对应值在平面坐标系中描出点(x,S),并用光滑的曲线将这些点连起来.
2.知识要点:
对于一个函数,如果把自变量与函数的每对对应值分别作为点的横、纵坐标,那么坐标平面内由这些点组成的图形,就是这个函数的 .
四、自学自测
试画出函数y=2x的图象,并判断点(2,1),(1,2),(-2,4),(-3.5,-7)是否在该函数图象上.
x
y
五、我的疑惑(反思)
_____________________________________________________________________
要点探究
探究点1:函数的图象
例1:画出下列函数的图象:(1)y=2x+1;(2).
要点归纳:画函数图象的一般步骤:
第一步,列表——表中给出一些自变量的值及其 ;
第二步,描点——在平面直角坐标系中,以自变量的值为 ,相应的函数值为 ,描出表格中数值对应的各点;
第三步:连线——按照横坐标 的顺序,把所描出的各点用 连接起来.
问题1:(1)函数y=2x+1的图象是一条 线,当自变量的值越来越大时,对应的函数值 .点(-0.5,1),(1.5,4)是否在该函数的图象上?
(2)函数的图象是两条 线,当x<0时,y随x的增大而 ;当x>0时,y随x的增大而 .点(2,3),(4,2)是否在该函数的图象上?
方法总结:通常的方法是把点的横坐标(即自变量x)的取值代入解析式求出相应的函数值y的值,看是否等于该点的纵坐标,如果等于,则该点在函数图象上;如不等,则该点不在函数图象上.
二、精讲点拨
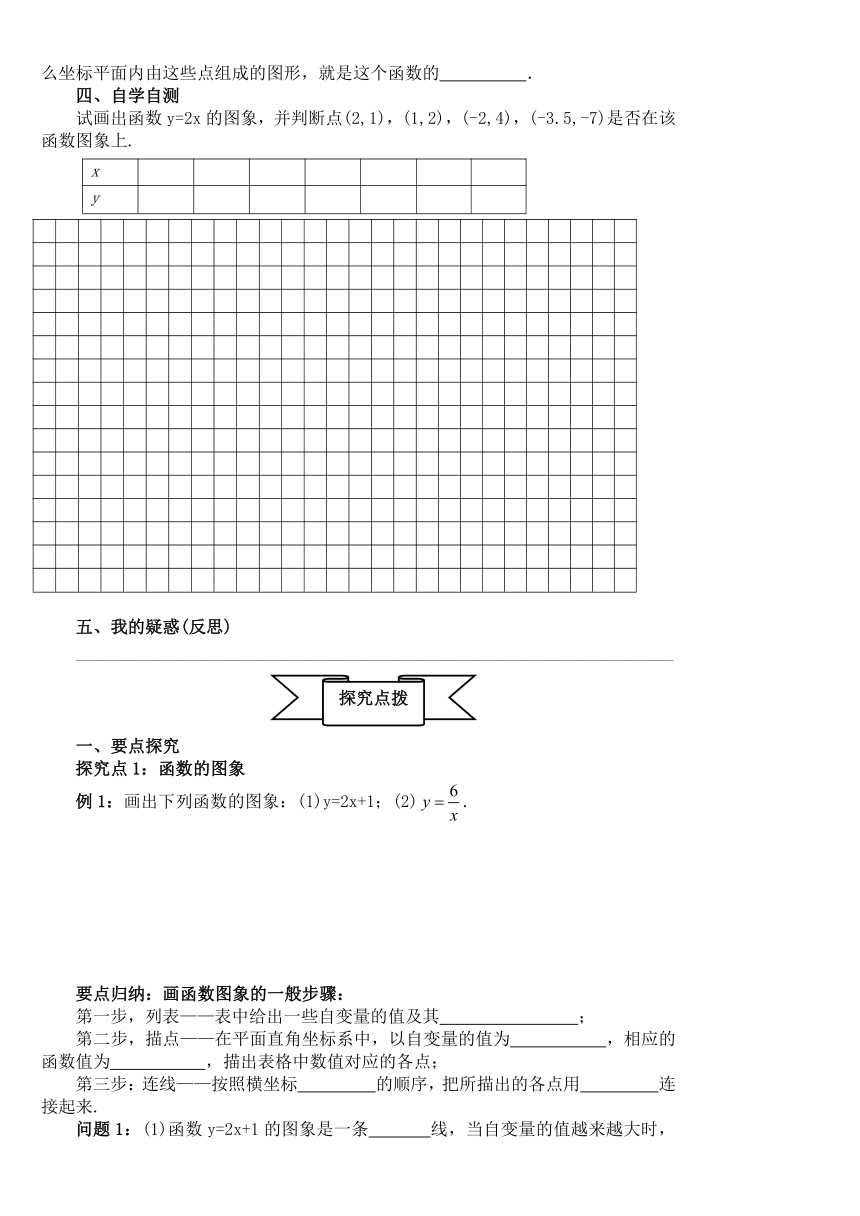
问题2:下图是自动测温仪记录的图象,它反映了北京的春季某天气温 T 如何随时间 t 的变化而变化.
你从图象中得到了哪些信息?
(1)从这个函数图象可知:这一天中 气温最低( ), 时气温最高( ) ;
(2)从 至 气温呈下降状态,从4时至 14时气温呈上升状态,从
至 气温又呈下降状态.
(3)从图象中可以看出这一天中任一时刻的气温.
方法总结:解答图象信息题主要运用数形结合思想,化图象信息为数字信息.
主要步骤如下:(1)了解横、纵轴的意义;
(2)从__________上判定函数与自变量的关系;
(3)抓住图象中端点,拐点等特殊点的实际意义.
三、变式训练
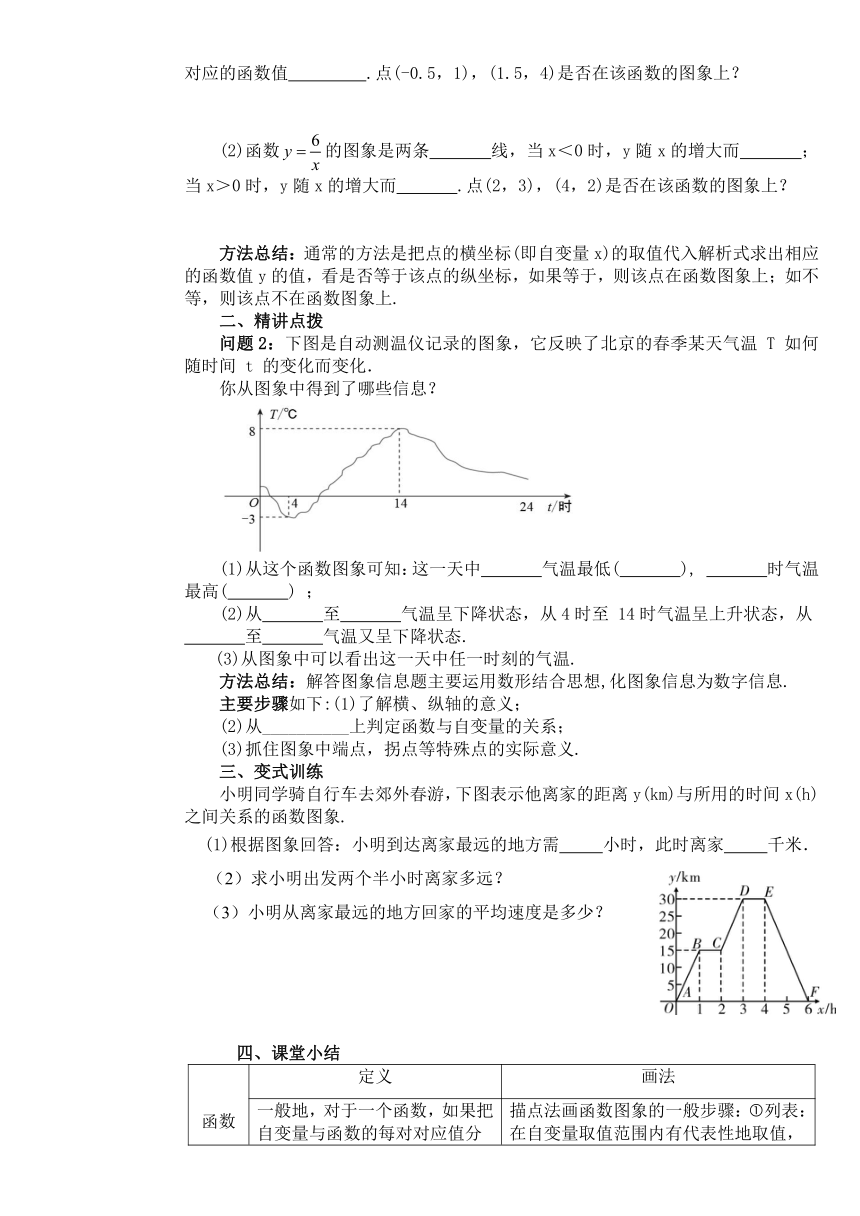
小明同学骑自行车去郊外春游,下图表示他离家的距离y(km)与所用的时间x(h)之间关系的函数图象.
(1)根据图象回答:小明到达离家最远的地方需 小时,此时离家 千米.
(2)求小明出发两个半小时离家多远?
(3)小明从离家最远的地方回家的平均速度是多少?
四、课堂小结
函数的图象 定义 画法
一般地,对于一个函数,如果把自变量与函数的每对对应值分别作为点的横、纵坐标,那么坐标平面内由这些点组成的图形,就是这个函数的图象. 描点法画函数图象的一般步骤:列表:在自变量取值范围内有代表性地取值,并求出相应的函数值;描点:一对对应值确定一个点;连线:按横坐标由小到大的顺序依次连接所描各点.
★1.某人早上进行登山活动,从山脚到山顶休息一会儿又沿原路返回,若用横轴表示时间t,纵轴表示与山脚距离h,那么下列四个图中反映全程h与t的关系图是( )
★★2.最近中旗连降雨雪,德岭山水库水位上涨.
如图表示某一天水位变化情况,0时的水位为警戒水
位.结合图象判断下列叙述不正确的是( )
A.8时水位最高
B.P点表示12时水位为0.6米
C.8时到16时水位都在下降
D.这一天水位均高于警戒水位
★★3.下面的图象反映的过程是:张强从家跑步去体育场,在那里锻炼了一阵后又走到文具店去买笔,然后散步走回家,图中x表示时间,y表示张强离家的距离.
体育场离张强家多远?张强从家到体育场用了多少时间?
体育场离文具店多远?
张强在文具店停留了多少时间?
张强从文具店回家的平均速度是多少?
我的反思(收获,不足)
分层作业
必做(教材 智慧学习 配套) 选做
参考答案:
课前检测
试题分析:(1)每行驶x千米,耗油0.1xL,即总油量减少0.1xL,则油箱中的油剩下(50﹣0.1x)L.
(2)从实际出发,x代表的实际意义为行驶里程,所以x不能为负数,又行驶中的耗油量为0.1xL,不能超过油箱中的汽油量50L.
(3)将x=200时,代入第一问中求出的x,y的关系式即可得出答案.
详解:(1)根据题意,每行驶x千米,耗油0.1xL,即总油量减少0.1xL,
则油箱中的油剩下(50﹣0.1x)L,
∴y与x的函数关系式为:y=50﹣0.1x;
(2)因为x代表的实际意义为行驶里程,所以x不能为负数,即x≥0;
又行驶中的耗油量为0.1x,不能超过油箱中现有汽油量的值50,
即0.1x≤50,解得,x≤500.
综上所述,自变量x的取值范围是0≤x≤500;
(3)当x=200时,代入x,y的关系式:
y=50﹣0.1×200=30.
所以,汽车行驶200km时,油桶中还有30L汽油.
变式训练:
试题分析:(1)根据分段函数的图象上点的坐标的意义可知:小明到达离家最远的地方需3小时;此时,他离家30千米;
(2)因为C(2,15)、D(3,30)在直线上,可知小明的运动是匀速运动,小明出发两个半小时恰好走到线段CD的中点处;
(3)用小明离家的距离除以返回的时间即可.
详解:(1)由图象可知小明到达离家最远的地方需3小时;此时,他离家30千米;
故填:3,30;
(2)由图象可知,CD段小明的运动是匀速运动.
又∵C(2,15)、D(3,30),
∴小明出发两个半小时恰好走到CD的中点处.
即当x=2.5时,y=22.5(千米)
答:出发两个半小时,小明离家22.5千米;
(3)从图象上看小明离家最远是距家30千米,返回时用了2小时,则
小明回家途中的速度为:30÷2=15(千米/小时).
答:小明从离家最远的地方回家的平均速度是15千米/小时.
星级达标:
1.试题分析:根据上山时h随着t的增加而增加,休息时h不再变化,下山时h随着时间t的增加而减小,据此可以判断.
详解:由题意得:上山时h随着t的增加而增加,休息时h不再变化,下山时h随着时间t的增加而减小,故选答案D.
2.试题分析:分析折线统计图表示每段时间中水位的高低,根据图形即可作出判断.
详解:A由折线统计图可知:8时水位为1.0米,是最高的,正确;
B P点表示12时水位为0.6米,又知警戒水位为0点,则P点表示12时水位高于警戒水位0.6米,正确;
C 8时到12时水位在下降,而12时到16时水位保持不变,故本选项不正确;
D 从图中可以看出,在这一天中所有的水位都在0点以上,所以这一天水位均高于警戒水位,正确;
故不正确的选项为C.
3.试题分析:(1)根据观察函数图象的纵坐标,可得距离,观察函数图象的横坐标,可得时间;
(2)根据函数图象的纵坐标,可得体育场离文具店的距离;
(3)根据观察函数图象的横坐标,可得在文具店停留的时间;
(4)根据观察函数图象的纵坐标,可得路程,根据观察函数图象的横坐标,可得回家的时间,根据路程与时间的关系可得答案.
详解:(1)由纵坐标看出体育场离张强家2.5千米,由横坐标看出张强从家去体育场用了15分钟;
(2)由纵坐标看出体育场离文具店2.5-1.5=1千米;
(2)由横坐标看出张强在文具店停留了65﹣45=20(分钟);
(3)由纵坐标看出文具店距张强家1.5千米,由横坐标看出从文具店回家用了95﹣65=30(分钟),所以张强从文具店回家的平均速度是1.5÷30=0.05千米/分,
答:张强从文具店回家平均每分钟走0.05千米.
第1课时 函数的图象
1.知道函数的图象的概念.
2.掌握画函数图象的一般步骤,能画出一些简单的函数图象.
3.能根据所给函数图象读出一些有用的信息.
学习重点:函数图象的意义及画法.
一、课前检测
一辆汽车的油箱中现有汽油50L,如果不再加油,那么油箱中的油量y(单位:L)随行驶里程x(单位:千米)的增加而减少,平均耗油量为0.1L/千米.
(1)写出表示y与x的函数关系式.
(2)指出自变量x的取值范围.
(3) 汽车行驶200千米时,油箱中还有多少汽油?
二、温故知新
在平面直角坐标系中,平面内的点可以用一对 来表示.即坐标平面内的 与有序数对是一一 的.
三、预习导航(预习教材第75-79页,标出你认为重要的关键词)
1.(1)正方形的面积S与边长x的函数解析式为 ,其中自变量x的取值范围是 .
(2)根据S与x的函数解析式填写下表:
x 0.5 1 1.5 2 2.5 3 3.5
S
(3)根据S与x的每组对应值在平面坐标系中描出点(x,S),并用光滑的曲线将这些点连起来.
2.知识要点:
对于一个函数,如果把自变量与函数的每对对应值分别作为点的横、纵坐标,那么坐标平面内由这些点组成的图形,就是这个函数的 .
四、自学自测
试画出函数y=2x的图象,并判断点(2,1),(1,2),(-2,4),(-3.5,-7)是否在该函数图象上.
x
y
五、我的疑惑(反思)
_____________________________________________________________________
要点探究
探究点1:函数的图象
例1:画出下列函数的图象:(1)y=2x+1;(2).
要点归纳:画函数图象的一般步骤:
第一步,列表——表中给出一些自变量的值及其 ;
第二步,描点——在平面直角坐标系中,以自变量的值为 ,相应的函数值为 ,描出表格中数值对应的各点;
第三步:连线——按照横坐标 的顺序,把所描出的各点用 连接起来.
问题1:(1)函数y=2x+1的图象是一条 线,当自变量的值越来越大时,对应的函数值 .点(-0.5,1),(1.5,4)是否在该函数的图象上?
(2)函数的图象是两条 线,当x<0时,y随x的增大而 ;当x>0时,y随x的增大而 .点(2,3),(4,2)是否在该函数的图象上?
方法总结:通常的方法是把点的横坐标(即自变量x)的取值代入解析式求出相应的函数值y的值,看是否等于该点的纵坐标,如果等于,则该点在函数图象上;如不等,则该点不在函数图象上.
二、精讲点拨
问题2:下图是自动测温仪记录的图象,它反映了北京的春季某天气温 T 如何随时间 t 的变化而变化.
你从图象中得到了哪些信息?
(1)从这个函数图象可知:这一天中 气温最低( ), 时气温最高( ) ;
(2)从 至 气温呈下降状态,从4时至 14时气温呈上升状态,从
至 气温又呈下降状态.
(3)从图象中可以看出这一天中任一时刻的气温.
方法总结:解答图象信息题主要运用数形结合思想,化图象信息为数字信息.
主要步骤如下:(1)了解横、纵轴的意义;
(2)从__________上判定函数与自变量的关系;
(3)抓住图象中端点,拐点等特殊点的实际意义.
三、变式训练
小明同学骑自行车去郊外春游,下图表示他离家的距离y(km)与所用的时间x(h)之间关系的函数图象.
(1)根据图象回答:小明到达离家最远的地方需 小时,此时离家 千米.
(2)求小明出发两个半小时离家多远?
(3)小明从离家最远的地方回家的平均速度是多少?
四、课堂小结
函数的图象 定义 画法
一般地,对于一个函数,如果把自变量与函数的每对对应值分别作为点的横、纵坐标,那么坐标平面内由这些点组成的图形,就是这个函数的图象. 描点法画函数图象的一般步骤:列表:在自变量取值范围内有代表性地取值,并求出相应的函数值;描点:一对对应值确定一个点;连线:按横坐标由小到大的顺序依次连接所描各点.
★1.某人早上进行登山活动,从山脚到山顶休息一会儿又沿原路返回,若用横轴表示时间t,纵轴表示与山脚距离h,那么下列四个图中反映全程h与t的关系图是( )
★★2.最近中旗连降雨雪,德岭山水库水位上涨.
如图表示某一天水位变化情况,0时的水位为警戒水
位.结合图象判断下列叙述不正确的是( )
A.8时水位最高
B.P点表示12时水位为0.6米
C.8时到16时水位都在下降
D.这一天水位均高于警戒水位
★★3.下面的图象反映的过程是:张强从家跑步去体育场,在那里锻炼了一阵后又走到文具店去买笔,然后散步走回家,图中x表示时间,y表示张强离家的距离.
体育场离张强家多远?张强从家到体育场用了多少时间?
体育场离文具店多远?
张强在文具店停留了多少时间?
张强从文具店回家的平均速度是多少?
我的反思(收获,不足)
分层作业
必做(教材 智慧学习 配套) 选做
参考答案:
课前检测
试题分析:(1)每行驶x千米,耗油0.1xL,即总油量减少0.1xL,则油箱中的油剩下(50﹣0.1x)L.
(2)从实际出发,x代表的实际意义为行驶里程,所以x不能为负数,又行驶中的耗油量为0.1xL,不能超过油箱中的汽油量50L.
(3)将x=200时,代入第一问中求出的x,y的关系式即可得出答案.
详解:(1)根据题意,每行驶x千米,耗油0.1xL,即总油量减少0.1xL,
则油箱中的油剩下(50﹣0.1x)L,
∴y与x的函数关系式为:y=50﹣0.1x;
(2)因为x代表的实际意义为行驶里程,所以x不能为负数,即x≥0;
又行驶中的耗油量为0.1x,不能超过油箱中现有汽油量的值50,
即0.1x≤50,解得,x≤500.
综上所述,自变量x的取值范围是0≤x≤500;
(3)当x=200时,代入x,y的关系式:
y=50﹣0.1×200=30.
所以,汽车行驶200km时,油桶中还有30L汽油.
变式训练:
试题分析:(1)根据分段函数的图象上点的坐标的意义可知:小明到达离家最远的地方需3小时;此时,他离家30千米;
(2)因为C(2,15)、D(3,30)在直线上,可知小明的运动是匀速运动,小明出发两个半小时恰好走到线段CD的中点处;
(3)用小明离家的距离除以返回的时间即可.
详解:(1)由图象可知小明到达离家最远的地方需3小时;此时,他离家30千米;
故填:3,30;
(2)由图象可知,CD段小明的运动是匀速运动.
又∵C(2,15)、D(3,30),
∴小明出发两个半小时恰好走到CD的中点处.
即当x=2.5时,y=22.5(千米)
答:出发两个半小时,小明离家22.5千米;
(3)从图象上看小明离家最远是距家30千米,返回时用了2小时,则
小明回家途中的速度为:30÷2=15(千米/小时).
答:小明从离家最远的地方回家的平均速度是15千米/小时.
星级达标:
1.试题分析:根据上山时h随着t的增加而增加,休息时h不再变化,下山时h随着时间t的增加而减小,据此可以判断.
详解:由题意得:上山时h随着t的增加而增加,休息时h不再变化,下山时h随着时间t的增加而减小,故选答案D.
2.试题分析:分析折线统计图表示每段时间中水位的高低,根据图形即可作出判断.
详解:A由折线统计图可知:8时水位为1.0米,是最高的,正确;
B P点表示12时水位为0.6米,又知警戒水位为0点,则P点表示12时水位高于警戒水位0.6米,正确;
C 8时到12时水位在下降,而12时到16时水位保持不变,故本选项不正确;
D 从图中可以看出,在这一天中所有的水位都在0点以上,所以这一天水位均高于警戒水位,正确;
故不正确的选项为C.
3.试题分析:(1)根据观察函数图象的纵坐标,可得距离,观察函数图象的横坐标,可得时间;
(2)根据函数图象的纵坐标,可得体育场离文具店的距离;
(3)根据观察函数图象的横坐标,可得在文具店停留的时间;
(4)根据观察函数图象的纵坐标,可得路程,根据观察函数图象的横坐标,可得回家的时间,根据路程与时间的关系可得答案.
详解:(1)由纵坐标看出体育场离张强家2.5千米,由横坐标看出张强从家去体育场用了15分钟;
(2)由纵坐标看出体育场离文具店2.5-1.5=1千米;
(2)由横坐标看出张强在文具店停留了65﹣45=20(分钟);
(3)由纵坐标看出文具店距张强家1.5千米,由横坐标看出从文具店回家用了95﹣65=30(分钟),所以张强从文具店回家的平均速度是1.5÷30=0.05千米/分,
答:张强从文具店回家平均每分钟走0.05千米.
