19.1.2函数的图象(第2课时)-2020-2021学年人教版八年级数学下册导学案(含详解)
文档属性
| 名称 | 19.1.2函数的图象(第2课时)-2020-2021学年人教版八年级数学下册导学案(含详解) |
|
|
| 格式 | doc | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-31 00:00:00 | ||
图片预览



文档简介
19.1.2 函数的图象
第2课时 函数的表示方法
学习目标:
1.知道函数的三种表示方法及其优缺点.
2.能用适当的方式表示实际问题中的变量之间的函数关系.
3能对函数关系进行分析,对变量的变化情况进行初步讨论.
学习重点:会表示简单实际问题中的变量之间的函数关系.
一、课前检测
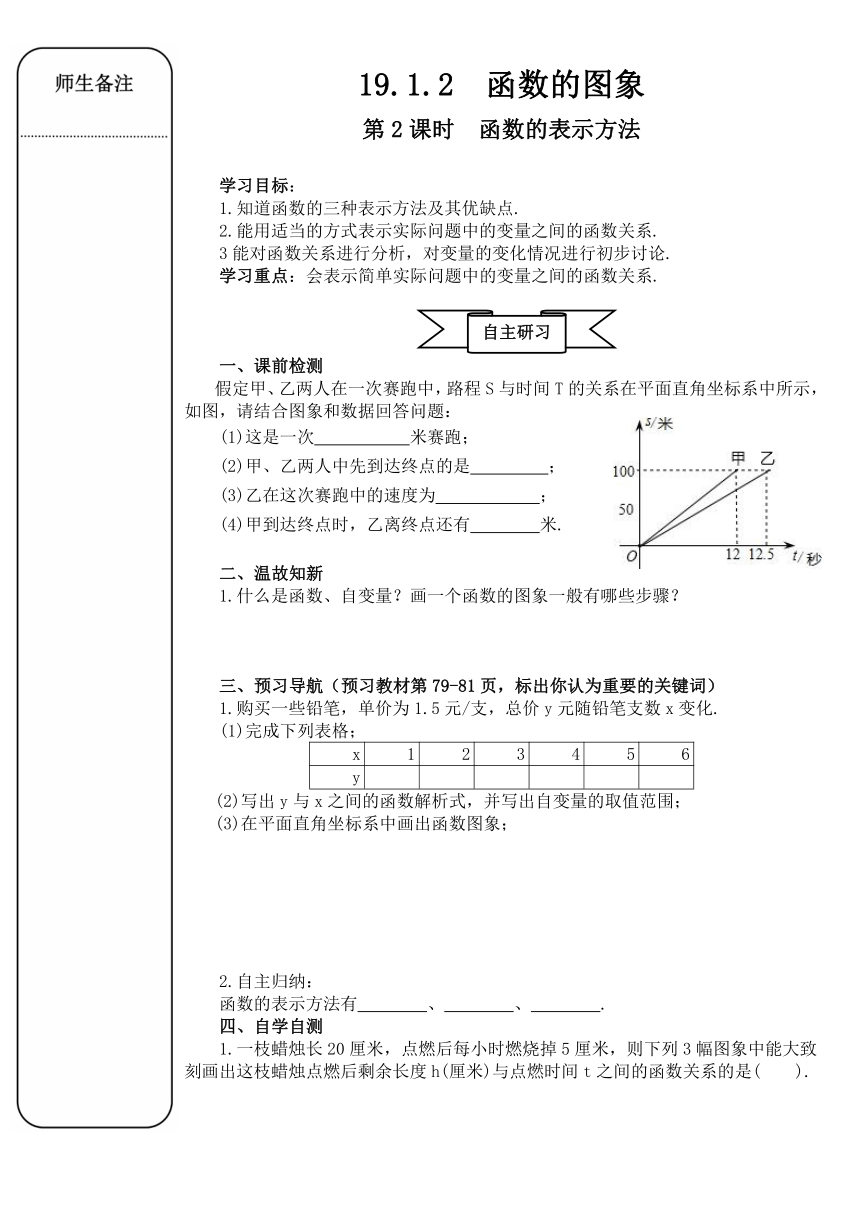
假定甲、乙两人在一次赛跑中,路程S与时间T的关系在平面直角坐标系中所示,如图,请结合图象和数据回答问题:
(1)这是一次 米赛跑;
(2)甲、乙两人中先到达终点的是 ;
(3)乙在这次赛跑中的速度为 ;
(4)甲到达终点时,乙离终点还有 米.
二、温故知新
1.什么是函数、自变量?画一个函数的图象一般有哪些步骤?
三、预习导航(预习教材第79-81页,标出你认为重要的关键词)
1.购买一些铅笔,单价为1.5元/支,总价y元随铅笔支数x变化.
(1)完成下列表格;
x 1 2 3 4 5 6
y
(2)写出y与x之间的函数解析式,并写出自变量的取值范围;
(3)在平面直角坐标系中画出函数图象;
自主归纳:
函数的表示方法有 、 、 .
四、自学自测
1.一枝蜡烛长20厘米,点燃后每小时燃烧掉5厘米,则下列3幅图象中能大致刻画出这枝蜡烛点燃后剩余长度h(厘米)与点燃时间t之间的函数关系的是( ).
2.据测试:拧不紧的水龙头每分钟滴出100滴水,每滴水约0.05毫升.小明同学洗手后,没有把水龙头拧紧,水龙头以测试的速度滴水,当小明离开x分钟后,水龙头滴出y毫升的水,请写出y与x之间的函数关系式是 .
五、我的疑惑(反思)
_____________________________________________________________________
要点探究
探究点:函数的表示方法
问题1:下图是某地气象站用自动温度记录仪描出的某一天的温度曲线,气温T是不是时间t 的函数?这里是怎样表示气温T与时间t之间的函数关系的?
问题2:正方形的面积S与边长x的取值如下表,面积S是不是边长x的函数?这里是怎样表示正方形面积S与边长x之间的函数关系的?
x 1 2 3 4 5 6
y 1 4 9 16 25 36
问题3:某城市居民用的天然气,1m3收费2.88元,使用x(m3) 天然气应缴纳的费用y(元)为y = ____________. y是不是x 的函数?
问题4:以上三种表示函数的方法各有什么优点?
要点归纳:
____________法:准确地反映了函数与自变量之间的数量关系.
2.____________法:具体地反映了函数与自变量的数值对应关系.
3.____________法:直观地反映了函数随自变量的变化而变化的规律.
二、精讲点拨
例1:要做一个面积为12 m2的矩形花坛,该花坛的一边长为 x m,周长为 y m.
(1)变量 y 是变量 x 的函数吗?如果是,写出自变量的取值范围;
(2)能求出这个问题的函数解析式吗?
(3)当 x 的值分别为1,2,3,4,5,6 时,请列表表示变量之间的对应关系;
(4)能画出这个函数的图象吗?
例2:已知火车站托运行李的费用C(元)和托运行李的重量P(千克)(P为整数)的对应关系如下表所示:
P 1 2 3 4 5 ...
C 2 2.5 3 3.5 4 ...
(1) 写出C与P之间的函数解析式.
(2)已知小周的所要托运的行李重12千克,请问小周托运行李的费用为多少元?
(3)小李托运行李花了15元钱,请问小李的行李重多少千克?
三、变式训练
已知等腰三角形的面积为30cm2,设它的底边长为xcm,底边上的高为ycm
(1)求底边上的高y随底边长x变化的函数解析式.并求自变量的取值范围.
(2)当底边长为10cm时,底边上的高是多少cm?
四、课堂小结
函数的表示方法
列表法 解析式法 图象法
概念 通过列出自变量的值与对应函数值的表格来表示函数关系. 用数学式子表示函数关系. 把自变量与函数的每对对应值分别作为点的横、纵坐标,顺次连接这些点组成的图形,就是这个函数的图象.
优点 对表中已有自变量的每一个值,可一目了然地得出对应的函数值 能准确地反映自变量与函数的对应关系 能直观、形象地反映函数关系变化的趋势
缺点 列出对应值是有限的,不易得出自变量和函数之间的对应规律 不是所有函数都能用函数解析式表示出来 由自变量的值往往难以找到对应函数的准确值
★1.小明所在学校与家距离为2千米,某天他放学后骑自行车回家,行驶了5分钟后,因故停留10分钟,继续骑了5分钟到家.如图,能大致描述他回家过程中离家的距离s(千米)与所用时间t(分)之间的关系图象是( )
★2.某工厂投入生产一种机器,每台成本y(万元/台)与生产数量x(台)之间是函数关系,函数y与自变量x的部分对应值如下表:
x(单位:台) 10 20 30
y(单位:万元/台) 60 55 50
则y与x之间的关系式是( )
A.y=80- 2x B.y=40+ 2x C. D.
★★3.用列表法与解析式法表示n边形的内角和m(单位:度)是边数n的函数.
★★4.用解析式法与图象法表示等边三角形的周长是边长a的函数.
★★★5.一条小船沿直线向码头匀速前进.在0min ,2min,4min,6min时,测得小船与码头的距离分别为200m,150m,100m,50m.小船与码头的距离是时间的函数吗?如果是,写出函数的解析式,并画出函数图象.
我的反思(收获,不足)
分层作业
必做(教材 智慧学习 配套) 选做
参考答案:
课前检测
试题分析:本题考查了函数图象的读图能力,根据图象中特殊点的实际意义即可求出答案.
详解:分析图象可知:
(1)这是一次100米赛跑;
(2)甲、乙两人中先到达终点的是甲;
(3)乙在这次赛跑中的速度是100÷12.5=8米/秒;
(4)甲到达终点时,乙离终点还有8×(12.5-12)=4米.
故答案应填:(1)100;(2)甲;(3)8米/秒;(4)4.
自学自测
1.试题分析:随着时间的增多,蜡烛的高度就越来越小,由于时间和高度都为正值,所以函数图象只能在第一象限,由此即可求出答案.
详解:设蜡烛点燃后剩下h厘米时,燃烧了t小时,
则h与t的关系是为h=20﹣5t,
从函数关系式可以看出,t越大,h越小,
符合此条件的只有C.故选答案C.
2.试题分析:每分钟滴出100滴水,每滴水约0.05毫升,则一分钟滴水100×0.05毫升,则x分钟可滴100×0.05x毫升,据此即可求解.
详解:由题意,得y=100×0.05x,即y=5x.
精讲点拨
例1 试题分析:本题考查了函数的定义,及函数图象的画法.根据函数的定义可判断y是x的函数,根据矩形的面积公式和周长公式可得函数解析式,据此列表、描点、连线可画出这个函数的图象.
详解:(1)变量 y 是变量 x 的函数,自变量x的取值范围是x>0;
由题意,得y=2() (x>0);
例2 试题分析:(1)根据表格中的数据变化可以确定C与P之间的函数关系式;
(2)将P=12代入(1)中的函数解析式即可解答本题;
(3)将C=15代入(1)中的函数解析式即可解答本题.
详解:(1)C与P之间的函数关系式为C=0.5P+1.5;
(2)将P=12代入C=0.5P+1.5,得
C=0.5×12+1.5=7.5,
答:小周托运行李的费用为7.5元;
(3)将C=15代入C=0.5P+1.5,得
15=0.5P+1.5, 解得,P=27.
答:小李的行李重27千克.
变式训练
试题分析:(1)根据三角形的面积公式,可得y关于x的函数关系式;
(2)当x=10时,代入解析式可得y的值,即底边上的高.
详解:(1)由三角形的面积,得
y= (x>0).
(2)当x=10时,y==4.
即底边上的高是4cm.
星级达标:
1.试题分析:根据题意可得:他回家过程中离家的距离S(千米)与所用时间t(分)之间的关系有3个阶段;(1)骑行了5分钟,离家的距离减小;(2)因故停留10分钟,离家的距离不变;(3)继续骑了5分钟到家,离家的距离继续减小直到为0,据此可以做出判断.
详解:因为小强家所在学校离家距离为2千米,某天他放学后骑自行车回家,行使了5分钟后,因故停留10分钟,继续骑了5分钟到家,所以图象应分为三段,根据最后离家的距离为0.
故选:D.
2.试题分析:将表格中的数据依次代入各选项的解析式,即可做出判断.
详解:A选项,当x=20时,y=80-2×20=40≠55,该解析式不合题意;
B选项,当x=20时,y=40+2×20=80≠55,该解析式也不合题意;
C选项,经验证,当x=10,20,30时,求得的函数值均符合题意;
D选项,当x=20时,y=60-×20=50≠55,该解析式不合题意;
故选答案C.
3.试题分析:从一点和边上的其他点连接分成三角形的个数为点数减去2,也就是边数减2,由于三角形的内角和是180°,所以多边形内角和与它的边数关系:(边数﹣2)×180°.由此规律计算即可求解.
详解:
图 例
… n边形
边 数 3 4 5 … n
内角和 180°×(3﹣2) 180°×(4﹣2) 180°×(5﹣2) … 180°×(n﹣2)
故n边形的内角和m(单位:度)关于边数n的函数为m=180°×(n﹣2).
4.试题分析:先写出用边长a表示周长l的函数解析式l=3a,再画出图象即可.
详解:∵等边三角形的周长=边长×3,
∴解析式为l=3a (a>0).
它的图象为:
5.试题分析:根据题中数据可得:小船的速度为50÷2=25(m/min),设:小船与码头的距离为y m,时间为x min,结合题意即可求解.
详解:由题意得:小船的速度为50÷2=25(m/min),
设:小船与码头的距离为y m,时间为x min,
则y=200﹣25x,
故小船与码头的距离是时间的函数,函数关系式为:y=200﹣25x.
图象如下:
第2课时 函数的表示方法
学习目标:
1.知道函数的三种表示方法及其优缺点.
2.能用适当的方式表示实际问题中的变量之间的函数关系.
3能对函数关系进行分析,对变量的变化情况进行初步讨论.
学习重点:会表示简单实际问题中的变量之间的函数关系.
一、课前检测
假定甲、乙两人在一次赛跑中,路程S与时间T的关系在平面直角坐标系中所示,如图,请结合图象和数据回答问题:
(1)这是一次 米赛跑;
(2)甲、乙两人中先到达终点的是 ;
(3)乙在这次赛跑中的速度为 ;
(4)甲到达终点时,乙离终点还有 米.
二、温故知新
1.什么是函数、自变量?画一个函数的图象一般有哪些步骤?
三、预习导航(预习教材第79-81页,标出你认为重要的关键词)
1.购买一些铅笔,单价为1.5元/支,总价y元随铅笔支数x变化.
(1)完成下列表格;
x 1 2 3 4 5 6
y
(2)写出y与x之间的函数解析式,并写出自变量的取值范围;
(3)在平面直角坐标系中画出函数图象;
自主归纳:
函数的表示方法有 、 、 .
四、自学自测
1.一枝蜡烛长20厘米,点燃后每小时燃烧掉5厘米,则下列3幅图象中能大致刻画出这枝蜡烛点燃后剩余长度h(厘米)与点燃时间t之间的函数关系的是( ).
2.据测试:拧不紧的水龙头每分钟滴出100滴水,每滴水约0.05毫升.小明同学洗手后,没有把水龙头拧紧,水龙头以测试的速度滴水,当小明离开x分钟后,水龙头滴出y毫升的水,请写出y与x之间的函数关系式是 .
五、我的疑惑(反思)
_____________________________________________________________________
要点探究
探究点:函数的表示方法
问题1:下图是某地气象站用自动温度记录仪描出的某一天的温度曲线,气温T是不是时间t 的函数?这里是怎样表示气温T与时间t之间的函数关系的?
问题2:正方形的面积S与边长x的取值如下表,面积S是不是边长x的函数?这里是怎样表示正方形面积S与边长x之间的函数关系的?
x 1 2 3 4 5 6
y 1 4 9 16 25 36
问题3:某城市居民用的天然气,1m3收费2.88元,使用x(m3) 天然气应缴纳的费用y(元)为y = ____________. y是不是x 的函数?
问题4:以上三种表示函数的方法各有什么优点?
要点归纳:
____________法:准确地反映了函数与自变量之间的数量关系.
2.____________法:具体地反映了函数与自变量的数值对应关系.
3.____________法:直观地反映了函数随自变量的变化而变化的规律.
二、精讲点拨
例1:要做一个面积为12 m2的矩形花坛,该花坛的一边长为 x m,周长为 y m.
(1)变量 y 是变量 x 的函数吗?如果是,写出自变量的取值范围;
(2)能求出这个问题的函数解析式吗?
(3)当 x 的值分别为1,2,3,4,5,6 时,请列表表示变量之间的对应关系;
(4)能画出这个函数的图象吗?
例2:已知火车站托运行李的费用C(元)和托运行李的重量P(千克)(P为整数)的对应关系如下表所示:
P 1 2 3 4 5 ...
C 2 2.5 3 3.5 4 ...
(1) 写出C与P之间的函数解析式.
(2)已知小周的所要托运的行李重12千克,请问小周托运行李的费用为多少元?
(3)小李托运行李花了15元钱,请问小李的行李重多少千克?
三、变式训练
已知等腰三角形的面积为30cm2,设它的底边长为xcm,底边上的高为ycm
(1)求底边上的高y随底边长x变化的函数解析式.并求自变量的取值范围.
(2)当底边长为10cm时,底边上的高是多少cm?
四、课堂小结
函数的表示方法
列表法 解析式法 图象法
概念 通过列出自变量的值与对应函数值的表格来表示函数关系. 用数学式子表示函数关系. 把自变量与函数的每对对应值分别作为点的横、纵坐标,顺次连接这些点组成的图形,就是这个函数的图象.
优点 对表中已有自变量的每一个值,可一目了然地得出对应的函数值 能准确地反映自变量与函数的对应关系 能直观、形象地反映函数关系变化的趋势
缺点 列出对应值是有限的,不易得出自变量和函数之间的对应规律 不是所有函数都能用函数解析式表示出来 由自变量的值往往难以找到对应函数的准确值
★1.小明所在学校与家距离为2千米,某天他放学后骑自行车回家,行驶了5分钟后,因故停留10分钟,继续骑了5分钟到家.如图,能大致描述他回家过程中离家的距离s(千米)与所用时间t(分)之间的关系图象是( )
★2.某工厂投入生产一种机器,每台成本y(万元/台)与生产数量x(台)之间是函数关系,函数y与自变量x的部分对应值如下表:
x(单位:台) 10 20 30
y(单位:万元/台) 60 55 50
则y与x之间的关系式是( )
A.y=80- 2x B.y=40+ 2x C. D.
★★3.用列表法与解析式法表示n边形的内角和m(单位:度)是边数n的函数.
★★4.用解析式法与图象法表示等边三角形的周长是边长a的函数.
★★★5.一条小船沿直线向码头匀速前进.在0min ,2min,4min,6min时,测得小船与码头的距离分别为200m,150m,100m,50m.小船与码头的距离是时间的函数吗?如果是,写出函数的解析式,并画出函数图象.
我的反思(收获,不足)
分层作业
必做(教材 智慧学习 配套) 选做
参考答案:
课前检测
试题分析:本题考查了函数图象的读图能力,根据图象中特殊点的实际意义即可求出答案.
详解:分析图象可知:
(1)这是一次100米赛跑;
(2)甲、乙两人中先到达终点的是甲;
(3)乙在这次赛跑中的速度是100÷12.5=8米/秒;
(4)甲到达终点时,乙离终点还有8×(12.5-12)=4米.
故答案应填:(1)100;(2)甲;(3)8米/秒;(4)4.
自学自测
1.试题分析:随着时间的增多,蜡烛的高度就越来越小,由于时间和高度都为正值,所以函数图象只能在第一象限,由此即可求出答案.
详解:设蜡烛点燃后剩下h厘米时,燃烧了t小时,
则h与t的关系是为h=20﹣5t,
从函数关系式可以看出,t越大,h越小,
符合此条件的只有C.故选答案C.
2.试题分析:每分钟滴出100滴水,每滴水约0.05毫升,则一分钟滴水100×0.05毫升,则x分钟可滴100×0.05x毫升,据此即可求解.
详解:由题意,得y=100×0.05x,即y=5x.
精讲点拨
例1 试题分析:本题考查了函数的定义,及函数图象的画法.根据函数的定义可判断y是x的函数,根据矩形的面积公式和周长公式可得函数解析式,据此列表、描点、连线可画出这个函数的图象.
详解:(1)变量 y 是变量 x 的函数,自变量x的取值范围是x>0;
由题意,得y=2() (x>0);
例2 试题分析:(1)根据表格中的数据变化可以确定C与P之间的函数关系式;
(2)将P=12代入(1)中的函数解析式即可解答本题;
(3)将C=15代入(1)中的函数解析式即可解答本题.
详解:(1)C与P之间的函数关系式为C=0.5P+1.5;
(2)将P=12代入C=0.5P+1.5,得
C=0.5×12+1.5=7.5,
答:小周托运行李的费用为7.5元;
(3)将C=15代入C=0.5P+1.5,得
15=0.5P+1.5, 解得,P=27.
答:小李的行李重27千克.
变式训练
试题分析:(1)根据三角形的面积公式,可得y关于x的函数关系式;
(2)当x=10时,代入解析式可得y的值,即底边上的高.
详解:(1)由三角形的面积,得
y= (x>0).
(2)当x=10时,y==4.
即底边上的高是4cm.
星级达标:
1.试题分析:根据题意可得:他回家过程中离家的距离S(千米)与所用时间t(分)之间的关系有3个阶段;(1)骑行了5分钟,离家的距离减小;(2)因故停留10分钟,离家的距离不变;(3)继续骑了5分钟到家,离家的距离继续减小直到为0,据此可以做出判断.
详解:因为小强家所在学校离家距离为2千米,某天他放学后骑自行车回家,行使了5分钟后,因故停留10分钟,继续骑了5分钟到家,所以图象应分为三段,根据最后离家的距离为0.
故选:D.
2.试题分析:将表格中的数据依次代入各选项的解析式,即可做出判断.
详解:A选项,当x=20时,y=80-2×20=40≠55,该解析式不合题意;
B选项,当x=20时,y=40+2×20=80≠55,该解析式也不合题意;
C选项,经验证,当x=10,20,30时,求得的函数值均符合题意;
D选项,当x=20时,y=60-×20=50≠55,该解析式不合题意;
故选答案C.
3.试题分析:从一点和边上的其他点连接分成三角形的个数为点数减去2,也就是边数减2,由于三角形的内角和是180°,所以多边形内角和与它的边数关系:(边数﹣2)×180°.由此规律计算即可求解.
详解:
图 例
… n边形
边 数 3 4 5 … n
内角和 180°×(3﹣2) 180°×(4﹣2) 180°×(5﹣2) … 180°×(n﹣2)
故n边形的内角和m(单位:度)关于边数n的函数为m=180°×(n﹣2).
4.试题分析:先写出用边长a表示周长l的函数解析式l=3a,再画出图象即可.
详解:∵等边三角形的周长=边长×3,
∴解析式为l=3a (a>0).
它的图象为:
5.试题分析:根据题中数据可得:小船的速度为50÷2=25(m/min),设:小船与码头的距离为y m,时间为x min,结合题意即可求解.
详解:由题意得:小船的速度为50÷2=25(m/min),
设:小船与码头的距离为y m,时间为x min,
则y=200﹣25x,
故小船与码头的距离是时间的函数,函数关系式为:y=200﹣25x.
图象如下:
