19.2.1正比例函数的图象和性质-2020-2021学年人教版八年级数学下册导学案(含详解)
文档属性
| 名称 | 19.2.1正比例函数的图象和性质-2020-2021学年人教版八年级数学下册导学案(含详解) |  | |
| 格式 | doc | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-31 15:20:58 | ||
图片预览


文档简介
19.2.1 正比例函数
第2课时 正比例函数的图象和性质
学习目标:
1.知道正比例函数的图象的特点,会利用两点(法)画正比例函数的图象.
2.熟记正比例函数的性质.
3.能结合正比例函数的图象和性质解答有关问题.
学习重点:正比例函数的图象和性质及其应用.
一、课前检测
若y与x-1成正比例,x=8时,y=6.写出x与y之间的函数关系式,并分别求出x=4和x=-3时y的值.
二、温故知新
1.已知正比例函数y=3x,当x=0时,y= ;当x=1时,y= .
2.画函数图象的步骤有: 、 、 .
三、预习导航(预习教材第87-89页,标出你认为重要的关键词)
1.画出下列正比例函数的图象:
(1)y=2x,; (2)y=-1.5x,y=-4x.
2.函数y=2x,的图象的共同特点是________________________________;
函数y=-1.5x,y=-4x的图象的共同特点是________________________________.
3.自主归纳:
(1)函数y=kx (k是常数,k≠0)的图象是一条经过 的 ;
(2)k>0时,函数y=kx (k是常数,k≠0)的图象经过第 象限;
k<0时,函数y=kx (k是常数,k≠0)的图象经过第 象限;
(3)k>0时,函数值y随自变量x 的增大而 ;
k<0时,函数值y随自变量x 的增大而 .
四、自学自测
1.函数y=-3x的图象是经过点(0,__)和(1,___)的一条______,图象经过第_____、____象限,从左到右呈_____趋势,即y随x的增大而______.
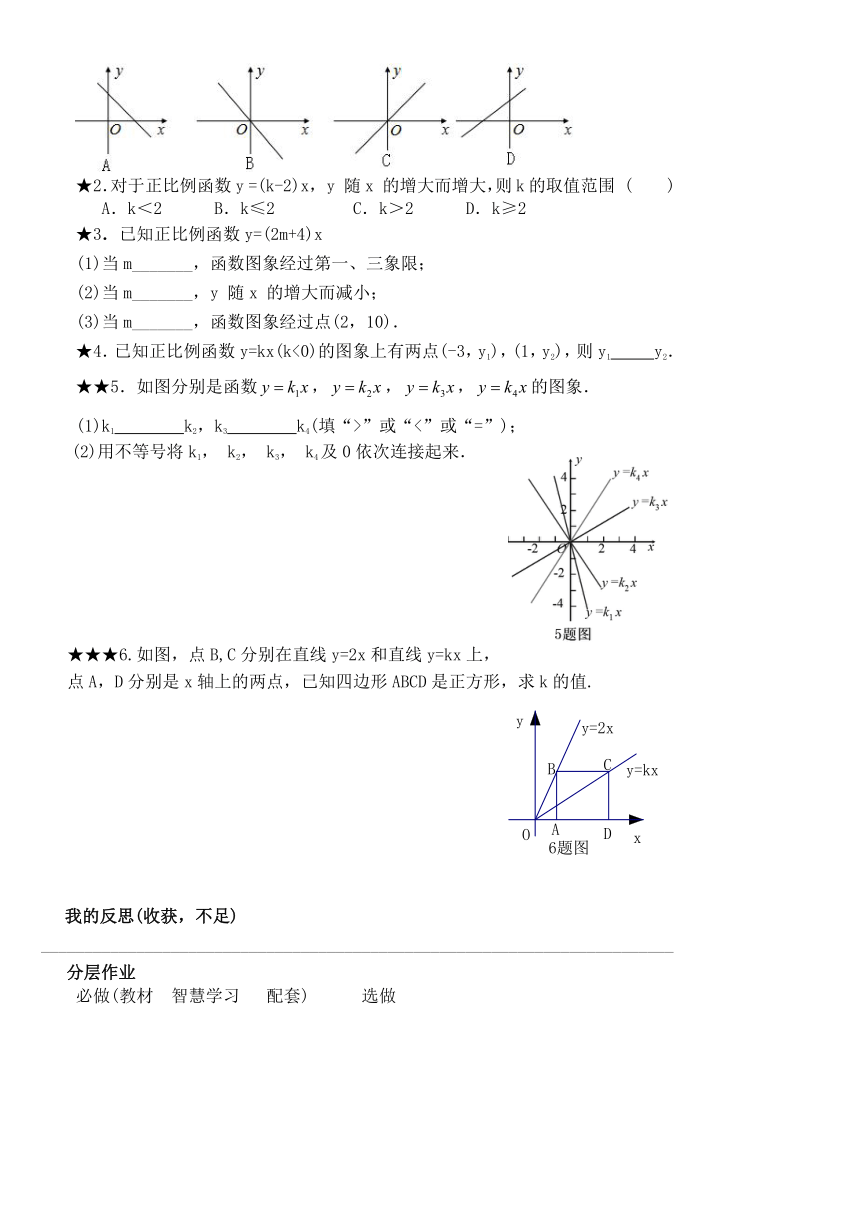
2.在平面直角坐标系中,正比例函数y =kx(k<0)的图象的大致位置可能是( ).
五、我的疑惑(反思)
__________________________________________________________________________________________________________________________________________________
要点探究
探究点1:正比例函数的图象
问题1:由预习导航可知,正比例函数的图象是什么样子的?
这样画正比例函数的图象时只需要确定几个点即可?
即学即练:1.用你认为最简单的方法画出下列函数的图象:
; (2)
方法总结:画正比例函数图象时我们只需描点(0,0)和点 (1,k),连线即可.
探究点2:正比例函数的性质
由预习导航可知,我们是从______、_______、________三个方面来研究正比例函数的性质的,具体来说是:
1.函数y=kx (k是常数,k≠0)的图象是一条经过 的 ;
2.k>0时,函数y=kx (k是常数,k≠0)的图象经过第 象限,函数值y随自变量x 的增大而 ;
3.k<0时,函数y=kx (k是常数,k≠0)的图象经过第 象限,函数值y随自变量x 的增大而 .
即学即练:
2.在函数y=x,y=3x, 和 中,随着x的增大,y的值分别如何变化?
二、精讲点拨
例1 已知正比例函数y=(k+1)x.
(1)若函数图象经过第一、三象限,求k的取值范围;
(2)若函数图象经过点(2,4),则k的值是多少?
例2 已知正比例函数y=mx的图象经过点(m,4),且y的值随着x值的增大而减小,求m的值.
方法总结:
三、变式训练
1.正比例函数y=x和y=3x中,随着x值的增大y的值都增加了,其中哪一个增加得更快?你能说明其中的道理吗?
2.正比例函数和y=-4x中,随着x值的增大y的值都减小了,其中哪一个减小得更快?你是如何判断的?
3.已知正比例函数y=(2m+1),y随x的增大而增大,求这个正比例函数解析式.
四、课堂小结
正比例函数y=kx(k≠0)
图象 正比例函数的图象是一条过原点的直线.
k>0 k<0
图象是自左向右上升的,经过第一、三象限 图象是自左向右下降的,经过第二、四象限
|k|越大,图象越陡(即越靠近y轴)
性质 y随x的增大而增大 y随x的增大而减小
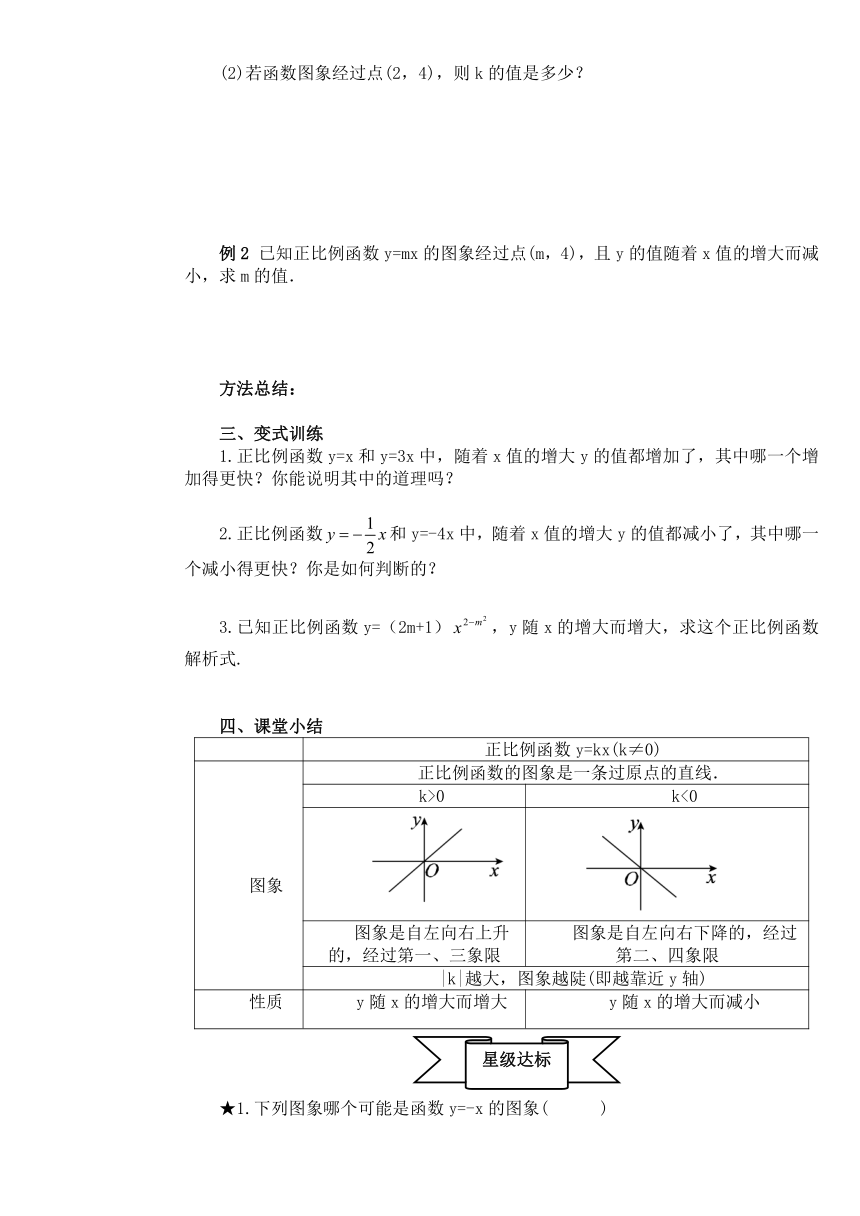
★1.下列图象哪个可能是函数y=-x的图象( )
★2.对于正比例函数y =(k-2)x, y 随x 的增大而增大,则k的取值范围 ( )
A.k<2 B.k≤2 C.k>2 D.k≥2
★3.已知正比例函数y=(2m+4)x
(1)当m_______,函数图象经过第一、三象限;
(2)当m_______,y 随x 的增大而减小;
(3)当m_______,函数图象经过点(2,10).
★4.已知正比例函数y=kx(k<0)的图象上有两点(-3,y1),(1,y2),则y1 y2.
★★5.如图分别是函数,,,的图象.
(1)k1 k2,k3 k4(填“>”或“<”或“=”);
(2)用不等号将k1, k2, k3, k4及0依次连接起来.
★★★6.如图,点B,C分别在直线y=2x和直线y=kx上,点A,D分别是x轴上的两点,已知四边形ABCD是正方形,求k的值.
我的反思(收获,不足)
_________________________________________________________________________
分层作业
必做(教材 智慧学习 配套) 选做
参考答案:
课前检测
试题分析:根据正比例函数定义,设y=k(x﹣1),把x=8,y=6代入求出k的值,从而得到x与y之间的函数关系式,然后分别计算出x=4和x=﹣3所对应的y的值.
详解:设y=k(x﹣1),
把x=8,y=6代入得k×(8﹣1)=6,解得k=,
所以y=(x﹣1)=x﹣,
所以x=y+1,
当x=4时,y=×4﹣=;
当x=﹣3时,y=×(﹣3)﹣=﹣.
即学即练:
1.试题分析:本题考查了正比例函数图象的画法.根据“两点确定一条直线”来作图即可.
(1)该函数图象是经过第一、三象限,且过原点的一条直线;
(2)该函数图象是经过第二、四象限,且过原点的一条直线.
详解:(1)该函数是正比例函数,函数图象是过原点的一条直线.
当x=0时,y=0; 当x=2时,y=3,
则该直线经过点(0,0),(2,3).
其图象如图所示;
(2)该函数是正比例函数,函数图象是过原点的一条直线.
当x=0时,y=0; 当x=1时,y=﹣3,
则该直线经过点(0,0),(1,﹣3).
其图象如图所示.
2.试题分析:本题考查了正比例函数的增减性,在y=kx (k≠0)中,当k>0时,y随x的增大而增大;当k<0时,y随x的增大而减小.据此可以判断.
详解:
在函数y=x中,比例系数k=1>0,随着x的增大,y的值也增大;
在函数y=3x中,比例系数k=3>0,随着x的增大,y的值也增大;
在函数中,比例系数k=<0,随着x的增大,y的值减小;
在函数y=-4x中,比例系数k=-4<0,随着x的增大,y的值减小.
精讲点拨
例1 试题分析:(1)根据正比例函数的图象经过第一、三象限列出关于k的不等式,求出k的取值范围即可;(2)由函数图象经过点(2,4),将(2,4)代入y=(k+1)x,解之可得.
详解:(1)∵比例函数y=(k+1)x的图象经过第一、三象限,
∴k+1>0,解得k>﹣1.
(2) ∵函数图象经过点(2,4),
将(2,4)代入y=(k+1)x,得
4=2(k+1),解得k=1.
例2 试题分析:将坐标(m,4)代入解析式,可求得m=±2,且y的值随x值的增大而减小,则m=﹣2.
详解∵正比例函数y=mx的图象经过点A(m,4),
∴4=m2. 解得m=±2.
∵y的值随x值的增大而减小
∴m=﹣2.
故答案为﹣2.
变式训练
1.试题分析:由题意知y=x和y=3x都是y随x的增大而增大,其中y=3x增加的更快些.
详解:y=3x增加的更快些.理由如下:
当x=a时,y=x=a,y=3x=3a;
现在自变量都增加了一个常数b(b>0),则
y=x=a+b,y=3x=3(a+b)=3a+3b.
与原函数值比较,y=x增加了b;y=3x增加了3b.
所以y=3x增加的更快些.
2.试题分析:由题意知和y=-4x都是y随x的增大而减小,其中y=-4x减小的更快些.
详解:y=-4x减小的更快些.理由如下:
当x=a时,=a,y=-4x=-4a;
现在自变量都增加了一个常数b(b>0),则
=ab,y=-4x=-4(a+b)=-4a-4b.
与原函数值比较,y=x减小了b;y=-4x减小了4b.
所以y=-4x减小的更快些.
3.试题分析:根据正比例函数的自变量的指数为1且比例系数不为零以及增减性即可求得m的值,代入解析式即可.
详解:∵正比例函数y=(2m+1)中,y随x的增大而增大,
∴, 解得:m=1,
∴正比例函数为y=3x.
星级达标:
试题分析:在正比例函数y=kx中,当k<0时,图象位于第二、四象限,据此可以做出判断.
详解:因为k=-1<0,所以y=-x的图象位于二、四象限,故选答案B.
2.试题分析:在正比例函数y=ax中,当a<0时,y随x的增大而减小,据此判断即可.
详解:∵正比例函数y=(k﹣2)x中,y随x的增大而减小
∴k﹣2<0,解得k<2
故选答案A.
3.试题分析:(1)根据函数图象经过一、三象限列出关于m的不等式,求出m的取值范围即可;(2)根据y随x的增大而减小列出关于m的不等式,求出m的取值范围即可;
(3)直接把点(2,10)代入正比例函数y=(2m+4)x,求出m的值即可.
详解:(1)∵函数图象经过一、三象限,
∴2m+4>0,解得m>﹣2;
(2)∵y随x的增大而减小,
∴2m+4<0,解得m<﹣2;
(3)∵点(2,10)在该函数图象上,
∴(2m+4)×2=10,解得m=.
4.试题分析:先根据题意判断出一次函数的增减性,再根据-3<1即可得出结论.
详解:∵一次函数y=kx中,k<0,
∴函数图象经过二、四象限,且y随x的增大而减小,
∵-3<1, ∴y1>y2. 故填“>”.
5.试题分析:对于,,,,我们可以令x=1,分别求出y的值,然后进行比较即可.
详解:(1)对于函数,令x=1则y=k1,对应点为(1,k1);
对于函数,令x=1则y=k2,对应点为(1,k2);
对于函数,令x=1则y=k3,对应点为(1,k3);
对于函数,令x=1则y=k4,对应点为(1,k4),如图所示:
由图可知k1<k2<0<k3<k4 ,
即 k1<k2,k3<k4.. 故答案是:<,<;
(2)由(1)可知k1<k2<0<k3<k4 .
6.试题分析:设正方形的边长为a,根据正方形的性质分别表示出B,C两点的坐标,再将C的坐标代入函数解析式中从而可求得k的值.
详解:设正方形的边长为a,则B的纵坐标是a,
把y=a代入直线y=2x的解析式,得x=.
则点B的坐标为(,a),点C的坐标为(+a,a),
把点C的坐标代入y=kx中得,a=k(+a),
解得k=.
第2课时 正比例函数的图象和性质
学习目标:
1.知道正比例函数的图象的特点,会利用两点(法)画正比例函数的图象.
2.熟记正比例函数的性质.
3.能结合正比例函数的图象和性质解答有关问题.
学习重点:正比例函数的图象和性质及其应用.
一、课前检测
若y与x-1成正比例,x=8时,y=6.写出x与y之间的函数关系式,并分别求出x=4和x=-3时y的值.
二、温故知新
1.已知正比例函数y=3x,当x=0时,y= ;当x=1时,y= .
2.画函数图象的步骤有: 、 、 .
三、预习导航(预习教材第87-89页,标出你认为重要的关键词)
1.画出下列正比例函数的图象:
(1)y=2x,; (2)y=-1.5x,y=-4x.
2.函数y=2x,的图象的共同特点是________________________________;
函数y=-1.5x,y=-4x的图象的共同特点是________________________________.
3.自主归纳:
(1)函数y=kx (k是常数,k≠0)的图象是一条经过 的 ;
(2)k>0时,函数y=kx (k是常数,k≠0)的图象经过第 象限;
k<0时,函数y=kx (k是常数,k≠0)的图象经过第 象限;
(3)k>0时,函数值y随自变量x 的增大而 ;
k<0时,函数值y随自变量x 的增大而 .
四、自学自测
1.函数y=-3x的图象是经过点(0,__)和(1,___)的一条______,图象经过第_____、____象限,从左到右呈_____趋势,即y随x的增大而______.
2.在平面直角坐标系中,正比例函数y =kx(k<0)的图象的大致位置可能是( ).
五、我的疑惑(反思)
__________________________________________________________________________________________________________________________________________________
要点探究
探究点1:正比例函数的图象
问题1:由预习导航可知,正比例函数的图象是什么样子的?
这样画正比例函数的图象时只需要确定几个点即可?
即学即练:1.用你认为最简单的方法画出下列函数的图象:
; (2)
方法总结:画正比例函数图象时我们只需描点(0,0)和点 (1,k),连线即可.
探究点2:正比例函数的性质
由预习导航可知,我们是从______、_______、________三个方面来研究正比例函数的性质的,具体来说是:
1.函数y=kx (k是常数,k≠0)的图象是一条经过 的 ;
2.k>0时,函数y=kx (k是常数,k≠0)的图象经过第 象限,函数值y随自变量x 的增大而 ;
3.k<0时,函数y=kx (k是常数,k≠0)的图象经过第 象限,函数值y随自变量x 的增大而 .
即学即练:
2.在函数y=x,y=3x, 和 中,随着x的增大,y的值分别如何变化?
二、精讲点拨
例1 已知正比例函数y=(k+1)x.
(1)若函数图象经过第一、三象限,求k的取值范围;
(2)若函数图象经过点(2,4),则k的值是多少?
例2 已知正比例函数y=mx的图象经过点(m,4),且y的值随着x值的增大而减小,求m的值.
方法总结:
三、变式训练
1.正比例函数y=x和y=3x中,随着x值的增大y的值都增加了,其中哪一个增加得更快?你能说明其中的道理吗?
2.正比例函数和y=-4x中,随着x值的增大y的值都减小了,其中哪一个减小得更快?你是如何判断的?
3.已知正比例函数y=(2m+1),y随x的增大而增大,求这个正比例函数解析式.
四、课堂小结
正比例函数y=kx(k≠0)
图象 正比例函数的图象是一条过原点的直线.
k>0 k<0
图象是自左向右上升的,经过第一、三象限 图象是自左向右下降的,经过第二、四象限
|k|越大,图象越陡(即越靠近y轴)
性质 y随x的增大而增大 y随x的增大而减小
★1.下列图象哪个可能是函数y=-x的图象( )
★2.对于正比例函数y =(k-2)x, y 随x 的增大而增大,则k的取值范围 ( )
A.k<2 B.k≤2 C.k>2 D.k≥2
★3.已知正比例函数y=(2m+4)x
(1)当m_______,函数图象经过第一、三象限;
(2)当m_______,y 随x 的增大而减小;
(3)当m_______,函数图象经过点(2,10).
★4.已知正比例函数y=kx(k<0)的图象上有两点(-3,y1),(1,y2),则y1 y2.
★★5.如图分别是函数,,,的图象.
(1)k1 k2,k3 k4(填“>”或“<”或“=”);
(2)用不等号将k1, k2, k3, k4及0依次连接起来.
★★★6.如图,点B,C分别在直线y=2x和直线y=kx上,点A,D分别是x轴上的两点,已知四边形ABCD是正方形,求k的值.
我的反思(收获,不足)
_________________________________________________________________________
分层作业
必做(教材 智慧学习 配套) 选做
参考答案:
课前检测
试题分析:根据正比例函数定义,设y=k(x﹣1),把x=8,y=6代入求出k的值,从而得到x与y之间的函数关系式,然后分别计算出x=4和x=﹣3所对应的y的值.
详解:设y=k(x﹣1),
把x=8,y=6代入得k×(8﹣1)=6,解得k=,
所以y=(x﹣1)=x﹣,
所以x=y+1,
当x=4时,y=×4﹣=;
当x=﹣3时,y=×(﹣3)﹣=﹣.
即学即练:
1.试题分析:本题考查了正比例函数图象的画法.根据“两点确定一条直线”来作图即可.
(1)该函数图象是经过第一、三象限,且过原点的一条直线;
(2)该函数图象是经过第二、四象限,且过原点的一条直线.
详解:(1)该函数是正比例函数,函数图象是过原点的一条直线.
当x=0时,y=0; 当x=2时,y=3,
则该直线经过点(0,0),(2,3).
其图象如图所示;
(2)该函数是正比例函数,函数图象是过原点的一条直线.
当x=0时,y=0; 当x=1时,y=﹣3,
则该直线经过点(0,0),(1,﹣3).
其图象如图所示.
2.试题分析:本题考查了正比例函数的增减性,在y=kx (k≠0)中,当k>0时,y随x的增大而增大;当k<0时,y随x的增大而减小.据此可以判断.
详解:
在函数y=x中,比例系数k=1>0,随着x的增大,y的值也增大;
在函数y=3x中,比例系数k=3>0,随着x的增大,y的值也增大;
在函数中,比例系数k=<0,随着x的增大,y的值减小;
在函数y=-4x中,比例系数k=-4<0,随着x的增大,y的值减小.
精讲点拨
例1 试题分析:(1)根据正比例函数的图象经过第一、三象限列出关于k的不等式,求出k的取值范围即可;(2)由函数图象经过点(2,4),将(2,4)代入y=(k+1)x,解之可得.
详解:(1)∵比例函数y=(k+1)x的图象经过第一、三象限,
∴k+1>0,解得k>﹣1.
(2) ∵函数图象经过点(2,4),
将(2,4)代入y=(k+1)x,得
4=2(k+1),解得k=1.
例2 试题分析:将坐标(m,4)代入解析式,可求得m=±2,且y的值随x值的增大而减小,则m=﹣2.
详解∵正比例函数y=mx的图象经过点A(m,4),
∴4=m2. 解得m=±2.
∵y的值随x值的增大而减小
∴m=﹣2.
故答案为﹣2.
变式训练
1.试题分析:由题意知y=x和y=3x都是y随x的增大而增大,其中y=3x增加的更快些.
详解:y=3x增加的更快些.理由如下:
当x=a时,y=x=a,y=3x=3a;
现在自变量都增加了一个常数b(b>0),则
y=x=a+b,y=3x=3(a+b)=3a+3b.
与原函数值比较,y=x增加了b;y=3x增加了3b.
所以y=3x增加的更快些.
2.试题分析:由题意知和y=-4x都是y随x的增大而减小,其中y=-4x减小的更快些.
详解:y=-4x减小的更快些.理由如下:
当x=a时,=a,y=-4x=-4a;
现在自变量都增加了一个常数b(b>0),则
=ab,y=-4x=-4(a+b)=-4a-4b.
与原函数值比较,y=x减小了b;y=-4x减小了4b.
所以y=-4x减小的更快些.
3.试题分析:根据正比例函数的自变量的指数为1且比例系数不为零以及增减性即可求得m的值,代入解析式即可.
详解:∵正比例函数y=(2m+1)中,y随x的增大而增大,
∴, 解得:m=1,
∴正比例函数为y=3x.
星级达标:
试题分析:在正比例函数y=kx中,当k<0时,图象位于第二、四象限,据此可以做出判断.
详解:因为k=-1<0,所以y=-x的图象位于二、四象限,故选答案B.
2.试题分析:在正比例函数y=ax中,当a<0时,y随x的增大而减小,据此判断即可.
详解:∵正比例函数y=(k﹣2)x中,y随x的增大而减小
∴k﹣2<0,解得k<2
故选答案A.
3.试题分析:(1)根据函数图象经过一、三象限列出关于m的不等式,求出m的取值范围即可;(2)根据y随x的增大而减小列出关于m的不等式,求出m的取值范围即可;
(3)直接把点(2,10)代入正比例函数y=(2m+4)x,求出m的值即可.
详解:(1)∵函数图象经过一、三象限,
∴2m+4>0,解得m>﹣2;
(2)∵y随x的增大而减小,
∴2m+4<0,解得m<﹣2;
(3)∵点(2,10)在该函数图象上,
∴(2m+4)×2=10,解得m=.
4.试题分析:先根据题意判断出一次函数的增减性,再根据-3<1即可得出结论.
详解:∵一次函数y=kx中,k<0,
∴函数图象经过二、四象限,且y随x的增大而减小,
∵-3<1, ∴y1>y2. 故填“>”.
5.试题分析:对于,,,,我们可以令x=1,分别求出y的值,然后进行比较即可.
详解:(1)对于函数,令x=1则y=k1,对应点为(1,k1);
对于函数,令x=1则y=k2,对应点为(1,k2);
对于函数,令x=1则y=k3,对应点为(1,k3);
对于函数,令x=1则y=k4,对应点为(1,k4),如图所示:
由图可知k1<k2<0<k3<k4 ,
即 k1<k2,k3<k4.. 故答案是:<,<;
(2)由(1)可知k1<k2<0<k3<k4 .
6.试题分析:设正方形的边长为a,根据正方形的性质分别表示出B,C两点的坐标,再将C的坐标代入函数解析式中从而可求得k的值.
详解:设正方形的边长为a,则B的纵坐标是a,
把y=a代入直线y=2x的解析式,得x=.
则点B的坐标为(,a),点C的坐标为(+a,a),
把点C的坐标代入y=kx中得,a=k(+a),
解得k=.
