教科版九年级上册物理习题课件 期末提分练案 第4讲 第2课时 技巧训练 电功率综合计算中的常用技巧(34张)
文档属性
| 名称 | 教科版九年级上册物理习题课件 期末提分练案 第4讲 第2课时 技巧训练 电功率综合计算中的常用技巧(34张) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 教科版 | ||
| 科目 | 物理 | ||
| 更新时间 | 2021-05-29 22:12:46 | ||
图片预览










文档简介
第4讲 电功率
JK版 九年级上
期末提分练案
第2课时 技巧训练
电功率综合计算中的常用技巧
见习题
见习题
1
2
3
答案呈现
提示:点击 进入习题
见习题
见习题
见习题
4
5
6
见习题
见习题
7
1.【2019·泸州】小明家电热水器铭牌标识为“220 V 1 000 W”。由于使用了多年,该电热水器中的电热丝明显氧化导致其电阻发生了变化,为准确测量氧化电热丝的实际电阻值,小明在家中把该电热水器单独接入220 V的家庭电路中工作5 min,发现电能表指示灯闪烁了242次,电能表规格如图所示。问:
(1)小明测得该电热水器的实际电功率是多少?
解:电能表指示灯闪烁了242次,消耗的电能
该电热水器的实际电功率
(2)该电热水器氧化电热丝的实际电阻值是多少?
解:该电热水器氧化电热丝的实际电阻值
(3)为恢复该电热水器的铭牌功率,可与氧化电热丝并联一段新的电热丝,则并联的这段电热丝的电阻值为多少?
解:电热水器铭牌标识的功率对应的电阻
为恢复该电热水器的铭牌功率,可与氧化电热丝并联一段新的电热丝,由并联电路中电阻的规律可得
即 解得R并=1 512.5 Ω。
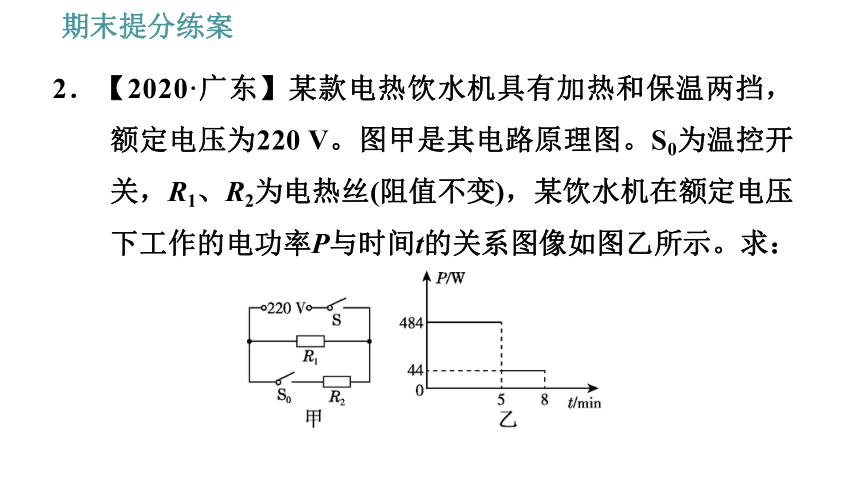
2.【2020·广东】某款电热饮水机具有加热和保温两挡,额定电压为220 V。图甲是其电路原理图。S0为温控开关,R1、R2为电热丝(阻值不变),某饮水机在额定电压下工作的电功率P与时间t的关系图像如图乙所示。求:
(1)饮水机处于加热挡阶段消耗的电能。
解:由图乙知,加热挡的功率为P加热=484 W,加热时间为t=5 min=300 s,饮水机处于加热挡阶段消耗的电能为:W=P加热t=484 W×300 s=1.452×105 J。
(2)饮水机处于保温挡时,通过R1的电流。
解:当开关S、S0闭合时,R1与R2并联,电路中的总电阻最小,根据 可知,饮水机的总功率最大,此时为加热状态;当只闭合开关S时,电路为R1的简单电路,饮水机处于保温状态。根据图乙知保温挡的功率为44 W;由P=UI知,保温挡时通过R1的电流为
(3)R2的阻值。
解:电热饮水机处于加热状态时电阻丝R2的电功率:P2=P加热-P1=P加热-P保温=484 W-44 W=440 W,由 可得,电阻R2的阻值:
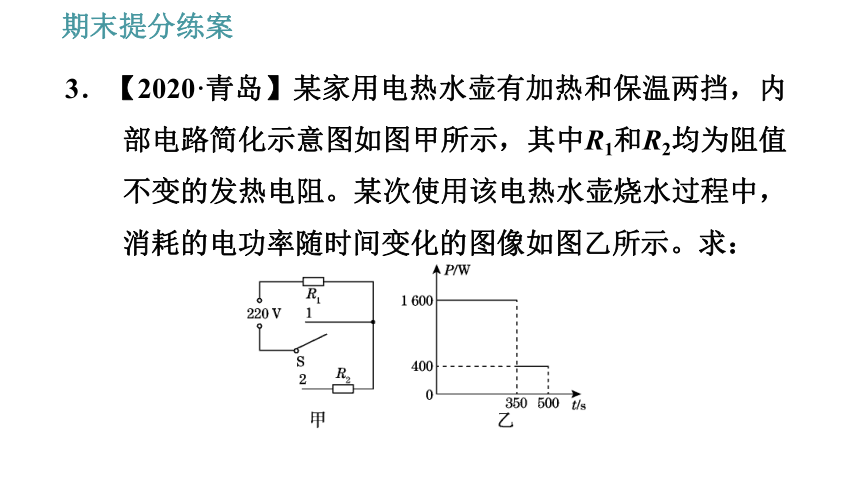
3.【2020·青岛】某家用电热水壶有加热和保温两挡,内部电路简化示意图如图甲所示,其中R1和R2均为阻值不变的发热电阻。某次使用该电热水壶烧水过程中,消耗的电功率随时间变化的图像如图乙所示。求:
(1)该电热水壶加热和保温时的电流之比。
解:由图乙知,加热功率为P1=1 600 W,保温功率为P2=400 W;根据P=UI可知,该电热水壶加热和保温时的电流之比为 I热:I温=P1:P2=1 600 W:400 W=4:1。
(2)电阻R2的阻值。
解:当开关S接1时,为R1的简单电路;当开关S接2时,两电阻串联,根据 可知,S接2时总功率最小,此时为保温挡,则S接1时为加热挡;加热状态时电路中的电阻:
保温时电路的总电阻为:
R2的阻值:R2=R串联-R1=121 Ω-30.25 Ω=90.75 Ω。
(3)给1.2 kg的水加热,使水温从20 ℃升至80 ℃,热水壶的工作效率为90%,需要多长加热时间。
解:水温从20 ℃升至80 ℃需要吸收的热量:Q=cmΔt=4.2×103 J/(kg·℃)×1.2 kg×(80 ℃-20 ℃)=3.024×105 J;由 可得需要的加热时间:
4.【中考·遵义】有一种挂式电热水器内部简化电路如图所示,该热水器设有高、中、低三挡,已知电热丝R1=55 Ω,高挡加热功率为1 100 W,电热转化效率为80%,水的比热容为4.2×103 J/(kg·℃)。
(1)将2 kg水从20 ℃加热到75 ℃需要吸收多少热量?
解:水吸收的热量Q吸=cm(t-t0)=4.2×103 J/(kg·℃)×2 kg×(75 ℃-20 ℃)=4.62×105 J。
(2)用高挡将2 kg水从20 ℃加热到75 ℃需要多长时间?
解:需要消耗的电能
需要加热的时间
(3)只闭合S、S2时,电热水器的电功率是多少?
解:由电路图可知,闭合S、S1、S2时,R1与R2并联,电路的总电阻最小,电路的总功率最大,电热水器处于高挡,此时电热丝R1的功率
因为电路的总功率等于各用电器功率之和,所以电热丝R2的功率P2=P高-P1=1 100 W-880 W=220 W;
只闭合S、S2时,电路为R2的简单电路,因为并联电路中各支路独立工作、互不影响,所以此时电热水器的电功率为220 W。
5.【中考·岳阳】图甲是某家用电熨斗,电路原理如图乙所示,R1、R2为发热体,R1的阻值为110 Ω,通过S1、S2实现温度控制。电源电压为电熨斗的额定电压220 V,电熨斗消耗的最大功率为660 W。
(1)只闭合S1,求通过R1的电流。
解:只闭合S1时,通过R1的电流
(2)只闭合S2,求R2在60 s内产生的热量。
解:闭合S1、S2时R1消耗的电功率P1=UI1=220 V×2 A=440 W;
只闭合S2时,只有R2接入电路,
R2消耗的电功率P2=P-P1=660 W-440 W=220 W;
R2在60 s内产生的热量Q2=W2=P2t=220 W×60 s=13 200 J。
(3)为适应更多衣料,小明对电路进行了改造,如图丙所示。当电熨斗控制开关S1、S2处于原低温工作状态不变时,移动滑片P,相应发热体的功率可在原功率的25%~100%之间变化。求滑动变阻器最大阻值至少为多少?
解:R2的电阻:
因为P1>P2,所以R2为低温挡发热电阻;
低温挡R2的发热功率为最大功率25%时的实际功率为
P2实=25%×220 W=55 W,
通过R2的实际电流为
此时R2与滑动变阻器串联,滑动变阻器两端的实际电压U变=U-U2实=220 V-110 V=110 V,I变=I2=0.5 A;滑动变阻器的最大电阻至少为
6.【2019·恩施】如图所示的为某电热器的电路图。R1和R2为电热丝,其中R1的规格为“220 V 110 W”且阻值不随温度变化而变化,电源电压保持220 V恒定不变。
(1)当S闭合时,10 min内电热器产生的热量是多少焦?
解:当S闭合时,电路为R1的简单电路,此时R1的功率P1=110 W,
则10 min内电热器产生的热量Q=W=P1t=110 W×10×60 s=6.6×104 J。
(2)当S断开时,R1的实际功率为39.6 W,则此时电热器的总功率为多大?
解:由 可得,R1的阻值
当S断开时,R1与R2串联,因为串联电路中各处的电流相等,所以,由P=UI=I2R可得,电路中的电流
此时电热器的总功率P=UI=220 V×0.3 A=66 W。
7.【2020·深圳】如图所示,电源电压恒定,小灯泡L标有“6 V 3 W”的字样(灯丝的电阻不随温度变化而变化)。当只闭合开关S1时,小灯泡恰好正常发光;当同时闭合S1和S2时,电流表的示数为0.8 A。求:
(1)只闭合S1时,电流表的示数。
解:只闭合S1时,只有灯泡L接入电路且灯泡正常发光,所以,电源的电压U=UL=6 V,由P=UI可得,小灯泡正常发光时的电流,即电流表的示数为:
(2)R0的阻值。
解:当开关S1、S2都闭合时,R0与L并联,电流表测干路电流,通过L的电流不变,通过R0的电流:I0=I-IL=0.8 A-0.5 A=0.3 A;由
可得R0的阻值:
(3)同时闭合S1和S2时,通电1 min电路产生的总热量。
解:当S1、S2都闭合时,通电1 min电路产生的总热量:
Q=W=UIt=6 V×0.8 A×60 s=288 J。
JK版 九年级上
期末提分练案
第2课时 技巧训练
电功率综合计算中的常用技巧
见习题
见习题
1
2
3
答案呈现
提示:点击 进入习题
见习题
见习题
见习题
4
5
6
见习题
见习题
7
1.【2019·泸州】小明家电热水器铭牌标识为“220 V 1 000 W”。由于使用了多年,该电热水器中的电热丝明显氧化导致其电阻发生了变化,为准确测量氧化电热丝的实际电阻值,小明在家中把该电热水器单独接入220 V的家庭电路中工作5 min,发现电能表指示灯闪烁了242次,电能表规格如图所示。问:
(1)小明测得该电热水器的实际电功率是多少?
解:电能表指示灯闪烁了242次,消耗的电能
该电热水器的实际电功率
(2)该电热水器氧化电热丝的实际电阻值是多少?
解:该电热水器氧化电热丝的实际电阻值
(3)为恢复该电热水器的铭牌功率,可与氧化电热丝并联一段新的电热丝,则并联的这段电热丝的电阻值为多少?
解:电热水器铭牌标识的功率对应的电阻
为恢复该电热水器的铭牌功率,可与氧化电热丝并联一段新的电热丝,由并联电路中电阻的规律可得
即 解得R并=1 512.5 Ω。
2.【2020·广东】某款电热饮水机具有加热和保温两挡,额定电压为220 V。图甲是其电路原理图。S0为温控开关,R1、R2为电热丝(阻值不变),某饮水机在额定电压下工作的电功率P与时间t的关系图像如图乙所示。求:
(1)饮水机处于加热挡阶段消耗的电能。
解:由图乙知,加热挡的功率为P加热=484 W,加热时间为t=5 min=300 s,饮水机处于加热挡阶段消耗的电能为:W=P加热t=484 W×300 s=1.452×105 J。
(2)饮水机处于保温挡时,通过R1的电流。
解:当开关S、S0闭合时,R1与R2并联,电路中的总电阻最小,根据 可知,饮水机的总功率最大,此时为加热状态;当只闭合开关S时,电路为R1的简单电路,饮水机处于保温状态。根据图乙知保温挡的功率为44 W;由P=UI知,保温挡时通过R1的电流为
(3)R2的阻值。
解:电热饮水机处于加热状态时电阻丝R2的电功率:P2=P加热-P1=P加热-P保温=484 W-44 W=440 W,由 可得,电阻R2的阻值:
3.【2020·青岛】某家用电热水壶有加热和保温两挡,内部电路简化示意图如图甲所示,其中R1和R2均为阻值不变的发热电阻。某次使用该电热水壶烧水过程中,消耗的电功率随时间变化的图像如图乙所示。求:
(1)该电热水壶加热和保温时的电流之比。
解:由图乙知,加热功率为P1=1 600 W,保温功率为P2=400 W;根据P=UI可知,该电热水壶加热和保温时的电流之比为 I热:I温=P1:P2=1 600 W:400 W=4:1。
(2)电阻R2的阻值。
解:当开关S接1时,为R1的简单电路;当开关S接2时,两电阻串联,根据 可知,S接2时总功率最小,此时为保温挡,则S接1时为加热挡;加热状态时电路中的电阻:
保温时电路的总电阻为:
R2的阻值:R2=R串联-R1=121 Ω-30.25 Ω=90.75 Ω。
(3)给1.2 kg的水加热,使水温从20 ℃升至80 ℃,热水壶的工作效率为90%,需要多长加热时间。
解:水温从20 ℃升至80 ℃需要吸收的热量:Q=cmΔt=4.2×103 J/(kg·℃)×1.2 kg×(80 ℃-20 ℃)=3.024×105 J;由 可得需要的加热时间:
4.【中考·遵义】有一种挂式电热水器内部简化电路如图所示,该热水器设有高、中、低三挡,已知电热丝R1=55 Ω,高挡加热功率为1 100 W,电热转化效率为80%,水的比热容为4.2×103 J/(kg·℃)。
(1)将2 kg水从20 ℃加热到75 ℃需要吸收多少热量?
解:水吸收的热量Q吸=cm(t-t0)=4.2×103 J/(kg·℃)×2 kg×(75 ℃-20 ℃)=4.62×105 J。
(2)用高挡将2 kg水从20 ℃加热到75 ℃需要多长时间?
解:需要消耗的电能
需要加热的时间
(3)只闭合S、S2时,电热水器的电功率是多少?
解:由电路图可知,闭合S、S1、S2时,R1与R2并联,电路的总电阻最小,电路的总功率最大,电热水器处于高挡,此时电热丝R1的功率
因为电路的总功率等于各用电器功率之和,所以电热丝R2的功率P2=P高-P1=1 100 W-880 W=220 W;
只闭合S、S2时,电路为R2的简单电路,因为并联电路中各支路独立工作、互不影响,所以此时电热水器的电功率为220 W。
5.【中考·岳阳】图甲是某家用电熨斗,电路原理如图乙所示,R1、R2为发热体,R1的阻值为110 Ω,通过S1、S2实现温度控制。电源电压为电熨斗的额定电压220 V,电熨斗消耗的最大功率为660 W。
(1)只闭合S1,求通过R1的电流。
解:只闭合S1时,通过R1的电流
(2)只闭合S2,求R2在60 s内产生的热量。
解:闭合S1、S2时R1消耗的电功率P1=UI1=220 V×2 A=440 W;
只闭合S2时,只有R2接入电路,
R2消耗的电功率P2=P-P1=660 W-440 W=220 W;
R2在60 s内产生的热量Q2=W2=P2t=220 W×60 s=13 200 J。
(3)为适应更多衣料,小明对电路进行了改造,如图丙所示。当电熨斗控制开关S1、S2处于原低温工作状态不变时,移动滑片P,相应发热体的功率可在原功率的25%~100%之间变化。求滑动变阻器最大阻值至少为多少?
解:R2的电阻:
因为P1>P2,所以R2为低温挡发热电阻;
低温挡R2的发热功率为最大功率25%时的实际功率为
P2实=25%×220 W=55 W,
通过R2的实际电流为
此时R2与滑动变阻器串联,滑动变阻器两端的实际电压U变=U-U2实=220 V-110 V=110 V,I变=I2=0.5 A;滑动变阻器的最大电阻至少为
6.【2019·恩施】如图所示的为某电热器的电路图。R1和R2为电热丝,其中R1的规格为“220 V 110 W”且阻值不随温度变化而变化,电源电压保持220 V恒定不变。
(1)当S闭合时,10 min内电热器产生的热量是多少焦?
解:当S闭合时,电路为R1的简单电路,此时R1的功率P1=110 W,
则10 min内电热器产生的热量Q=W=P1t=110 W×10×60 s=6.6×104 J。
(2)当S断开时,R1的实际功率为39.6 W,则此时电热器的总功率为多大?
解:由 可得,R1的阻值
当S断开时,R1与R2串联,因为串联电路中各处的电流相等,所以,由P=UI=I2R可得,电路中的电流
此时电热器的总功率P=UI=220 V×0.3 A=66 W。
7.【2020·深圳】如图所示,电源电压恒定,小灯泡L标有“6 V 3 W”的字样(灯丝的电阻不随温度变化而变化)。当只闭合开关S1时,小灯泡恰好正常发光;当同时闭合S1和S2时,电流表的示数为0.8 A。求:
(1)只闭合S1时,电流表的示数。
解:只闭合S1时,只有灯泡L接入电路且灯泡正常发光,所以,电源的电压U=UL=6 V,由P=UI可得,小灯泡正常发光时的电流,即电流表的示数为:
(2)R0的阻值。
解:当开关S1、S2都闭合时,R0与L并联,电流表测干路电流,通过L的电流不变,通过R0的电流:I0=I-IL=0.8 A-0.5 A=0.3 A;由
可得R0的阻值:
(3)同时闭合S1和S2时,通电1 min电路产生的总热量。
解:当S1、S2都闭合时,通电1 min电路产生的总热量:
Q=W=UIt=6 V×0.8 A×60 s=288 J。
同课章节目录
