10.2.1 平行线的判定 —三线八角课件-沪科版七年级数学下册(17张)
文档属性
| 名称 | 10.2.1 平行线的判定 —三线八角课件-沪科版七年级数学下册(17张) |

|
|
| 格式 | ppt | ||
| 文件大小 | 915.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-31 15:32:32 | ||
图片预览




文档简介
(共17张PPT)
课题导入
10.2.1
平行线的判定
—三线八角
课题导入
目标引领
目标引领
1、理解平行线的概念及相关性质,并掌握平行线的画法;
2、理解同位角、内错角、同旁内角的概念,能够辨认同位角、内错角、同旁内角.
约3分钟
独立自学一
独立自学
阅读课本P123,思考下列问题:
2、如何过直线外一点作与它平行的直线?
能作几条?
1、在
内
的两条直线叫平行线.
l
P
引导探究
引导探究
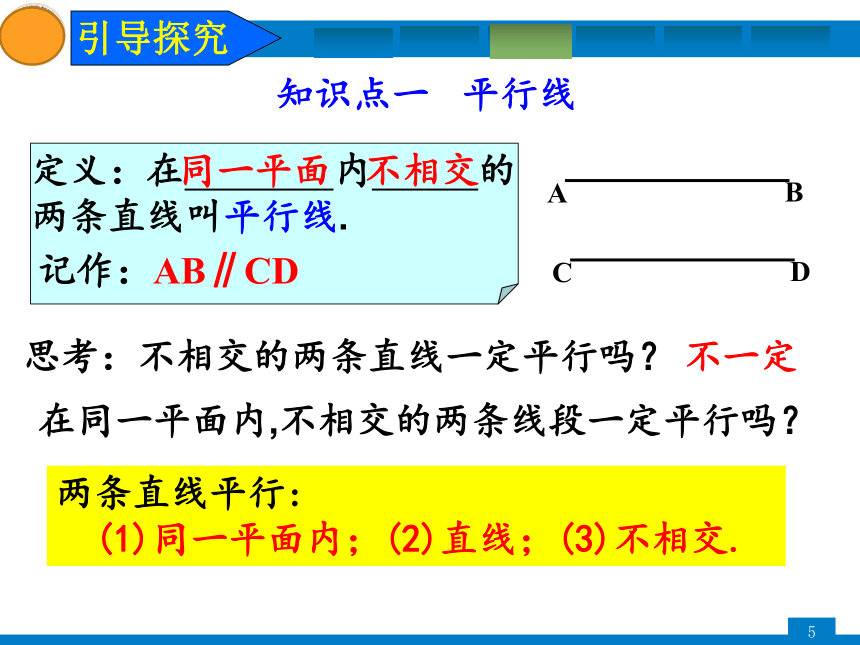
定义:在
内
的
两条直线叫平行线.
A
B
C
D
记作:AB∥CD
同一平面
不相交
思考:不相交的两条直线一定平行吗?
不一定
两条直线平行:
(1)同一平面内;(2)直线;(3)不相交.
在同一平面内,不相交的两条线段一定平行吗?
知识点一
平行线
引导探究
引导探究
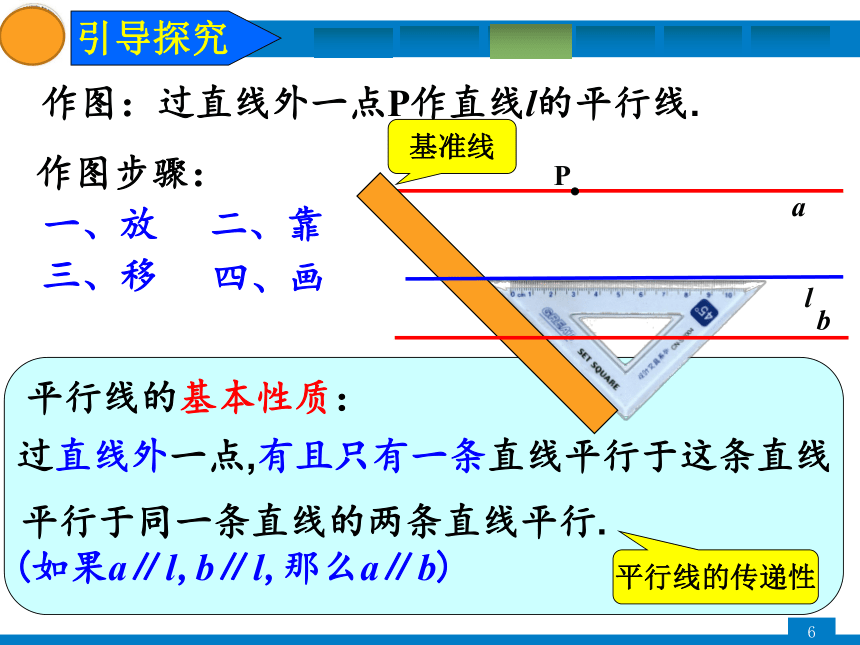
平行线的基本性质:
作图:过直线外一点P作直线l的平行线.
l
P
a
作图步骤:
一、放
四、画
二、靠
三、移
b
过直线外一点,有且只有一条直线平行于这条直线
平行于同一条直线的两条直线平行.
(如果a∥l,b∥l,那么a∥b)
基准线
平行线的传递性
约3分钟
独立自学二
独立自学
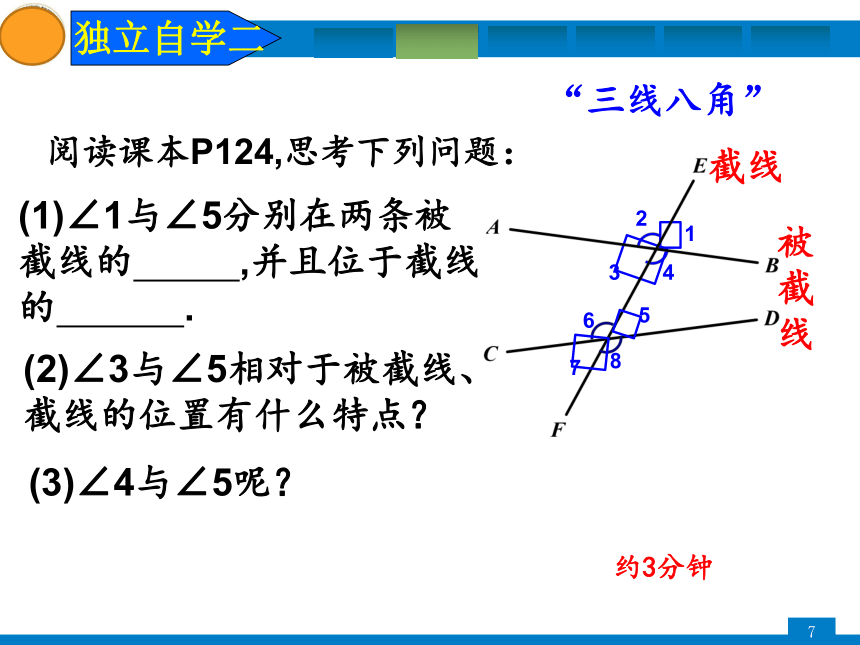
(1)∠1与∠5分别在两条被截线的
,并且位于截线的
.
1
2
3
4
5
6
7
8
“三线八角”
被截线
截线
阅读课本P124,思考下列问题:
(2)∠3与∠5相对于被截线、截线的位置有什么特点?
(3)∠4与∠5呢?
引导探究
引导探究
与被截线位置
与截线位置
形状
∠1,∠5
∠3,∠5
∠4,∠5
同侧
1
2
3
4
5
6
7
8
被截线
截线
1
5
同旁
同位角
F
之间
两旁
内错角
3
5
Z
之间
同旁
同旁内角
5
4
U
请你找出其它的同位角.
内错角
同旁内角
知识点二
“三线八角”
引导探究
引导探究
1、下列各图
与
是同位角吗?
1
2
(
)
(
)
1
2
(
)
1
2
方法指导:找准截线(两个角的公共边所在直线)
2、如图,(1)∠1与∠2是
角,它们是由直线
、
被直线
所截得;
(2)∠1与∠4是
角,它们是由直线
、
被直线
所截得;
(3)∠3与∠4是
角,它们是由直线
、
被直线
所截得;
同旁内
AB
CD
EF
同位
EF
MN
AB
内错
AB
CD
MN
知识点二
“三线八角”
引导探究
引导探究
引导探究
3、如图,直线AB,CD被直线CE所截,与∠1成内错角的是
;与∠1成同旁内角的是
.
当直线
,
被直线
所截时,∠2与∠5成内错角,∠2与
成同旁内角.
∠3
∠BEC
CD
AB
方法指导:找到截线与被截线,排除其他直线干扰
DE
∠AED
4.如图直线DE、BC被直线AB所截,
(1)∠1和∠2、∠1和∠3、∠1和∠4各是什么角?
(2)如果∠1=∠4,哪么∠1和∠2相等吗?∠1和∠3互补吗?为什么?
E
2
4
3
1
解:(1)∠1和∠2是内错角;∠1和∠3是同旁内角;
∠1和∠4是同位角。
(2)∵∠1=∠4(已知)
∠4=∠2
(对顶角相等)
∴∠1=∠2.
∵∠4+∠3=180°(邻补角定义)
∠1=∠4(已知)
∴∠1+∠3=180°
即∠1和∠3互补.
D
A
B
C
引导探究
5.如图,回答:
1
2
3
4
5
6
7
8
A
B
C
D
E
若直线DE,AB被AC所截,同旁内角有几对?
若直线DE,AC被AB所截,同旁内角有几对?
关键:要先分清哪两条直线被哪一条直线所截
9
12
11
10
引导探究
引导探究
引导探究
6、根据图形,完成下列问题:
(1)∠B的同位角有
.
(3)∠B的同旁内角有
.
(2)∠C的内错角有
.
∠EAD
∠EAC
∠DAC
∠EAC
∠BAC
∠C
∠DAB
你有什么收获或疑惑?
目标升华
目标升华
一概念:在同一平面内不相交的两条直线叫平行线.
两性质:
1、过直线外一点,有且只有一条直线平行于这条直线.
2、如果直线a∥l,b∥l,那么直线a∥b.(传递性)
三种角:同位角
内错角
同旁内角
当堂诊学
当堂诊学
C
1、下列说法正确的是( )
A.过直线AB外一点P画AB的平行线,可以画无数条
B.在同一平面内,平行于AB的直线只有一条
C.过直线外一点有且只有一条直线与这条直线平行
D.经过一点,有且只有一条直线和已知直线平行
2、如图直线DE、BC被直线AB所截,
(1)∠1和∠2、∠1和∠3、∠1和∠4各是什么角?
(2)如果∠1=∠4,哪么∠1和∠2相等吗?
∠1和∠3互补吗?为什么?
E
2
4
3
1
D
A
B
1、课后练习1、2、3、4;
2、预习
强化补清
强化补清
课题导入
10.2.1
平行线的判定
—三线八角
课题导入
目标引领
目标引领
1、理解平行线的概念及相关性质,并掌握平行线的画法;
2、理解同位角、内错角、同旁内角的概念,能够辨认同位角、内错角、同旁内角.
约3分钟
独立自学一
独立自学
阅读课本P123,思考下列问题:
2、如何过直线外一点作与它平行的直线?
能作几条?
1、在
内
的两条直线叫平行线.
l
P
引导探究
引导探究
定义:在
内
的
两条直线叫平行线.
A
B
C
D
记作:AB∥CD
同一平面
不相交
思考:不相交的两条直线一定平行吗?
不一定
两条直线平行:
(1)同一平面内;(2)直线;(3)不相交.
在同一平面内,不相交的两条线段一定平行吗?
知识点一
平行线
引导探究
引导探究
平行线的基本性质:
作图:过直线外一点P作直线l的平行线.
l
P
a
作图步骤:
一、放
四、画
二、靠
三、移
b
过直线外一点,有且只有一条直线平行于这条直线
平行于同一条直线的两条直线平行.
(如果a∥l,b∥l,那么a∥b)
基准线
平行线的传递性
约3分钟
独立自学二
独立自学
(1)∠1与∠5分别在两条被截线的
,并且位于截线的
.
1
2
3
4
5
6
7
8
“三线八角”
被截线
截线
阅读课本P124,思考下列问题:
(2)∠3与∠5相对于被截线、截线的位置有什么特点?
(3)∠4与∠5呢?
引导探究
引导探究
与被截线位置
与截线位置
形状
∠1,∠5
∠3,∠5
∠4,∠5
同侧
1
2
3
4
5
6
7
8
被截线
截线
1
5
同旁
同位角
F
之间
两旁
内错角
3
5
Z
之间
同旁
同旁内角
5
4
U
请你找出其它的同位角.
内错角
同旁内角
知识点二
“三线八角”
引导探究
引导探究
1、下列各图
与
是同位角吗?
1
2
(
)
(
)
1
2
(
)
1
2
方法指导:找准截线(两个角的公共边所在直线)
2、如图,(1)∠1与∠2是
角,它们是由直线
、
被直线
所截得;
(2)∠1与∠4是
角,它们是由直线
、
被直线
所截得;
(3)∠3与∠4是
角,它们是由直线
、
被直线
所截得;
同旁内
AB
CD
EF
同位
EF
MN
AB
内错
AB
CD
MN
知识点二
“三线八角”
引导探究
引导探究
引导探究
3、如图,直线AB,CD被直线CE所截,与∠1成内错角的是
;与∠1成同旁内角的是
.
当直线
,
被直线
所截时,∠2与∠5成内错角,∠2与
成同旁内角.
∠3
∠BEC
CD
AB
方法指导:找到截线与被截线,排除其他直线干扰
DE
∠AED
4.如图直线DE、BC被直线AB所截,
(1)∠1和∠2、∠1和∠3、∠1和∠4各是什么角?
(2)如果∠1=∠4,哪么∠1和∠2相等吗?∠1和∠3互补吗?为什么?
E
2
4
3
1
解:(1)∠1和∠2是内错角;∠1和∠3是同旁内角;
∠1和∠4是同位角。
(2)∵∠1=∠4(已知)
∠4=∠2
(对顶角相等)
∴∠1=∠2.
∵∠4+∠3=180°(邻补角定义)
∠1=∠4(已知)
∴∠1+∠3=180°
即∠1和∠3互补.
D
A
B
C
引导探究
5.如图,回答:
1
2
3
4
5
6
7
8
A
B
C
D
E
若直线DE,AB被AC所截,同旁内角有几对?
若直线DE,AC被AB所截,同旁内角有几对?
关键:要先分清哪两条直线被哪一条直线所截
9
12
11
10
引导探究
引导探究
引导探究
6、根据图形,完成下列问题:
(1)∠B的同位角有
.
(3)∠B的同旁内角有
.
(2)∠C的内错角有
.
∠EAD
∠EAC
∠DAC
∠EAC
∠BAC
∠C
∠DAB
你有什么收获或疑惑?
目标升华
目标升华
一概念:在同一平面内不相交的两条直线叫平行线.
两性质:
1、过直线外一点,有且只有一条直线平行于这条直线.
2、如果直线a∥l,b∥l,那么直线a∥b.(传递性)
三种角:同位角
内错角
同旁内角
当堂诊学
当堂诊学
C
1、下列说法正确的是( )
A.过直线AB外一点P画AB的平行线,可以画无数条
B.在同一平面内,平行于AB的直线只有一条
C.过直线外一点有且只有一条直线与这条直线平行
D.经过一点,有且只有一条直线和已知直线平行
2、如图直线DE、BC被直线AB所截,
(1)∠1和∠2、∠1和∠3、∠1和∠4各是什么角?
(2)如果∠1=∠4,哪么∠1和∠2相等吗?
∠1和∠3互补吗?为什么?
E
2
4
3
1
D
A
B
1、课后练习1、2、3、4;
2、预习
强化补清
强化补清
