第八章成对数据的统计分析复习课教学课件(共18张PPT)——2020-2021学年高二下学期人教A版(2019)选择性必修第三册第八章成对数据的统计分析
文档属性
| 名称 | 第八章成对数据的统计分析复习课教学课件(共18张PPT)——2020-2021学年高二下学期人教A版(2019)选择性必修第三册第八章成对数据的统计分析 |  | |
| 格式 | pptx | ||
| 文件大小 | 382.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-01 09:18:26 | ||
图片预览


文档简介
第八章成对数据的统计分析的应用
——复习参考题
回归分析
独立性检验
01
02
知识回顾
1
散点图
通过散点图了解变量关系,非线性转化为线性的,然后用最小二乘法建立回归模型,接着通过分析残差、指标衡量模型的拟合效果
2
非线性线性
3
回归方程
4
问题预测
回归分析
01
1
列联表
2
假设变量无关
3
随机变量
4
问题决策
独立性检验
02
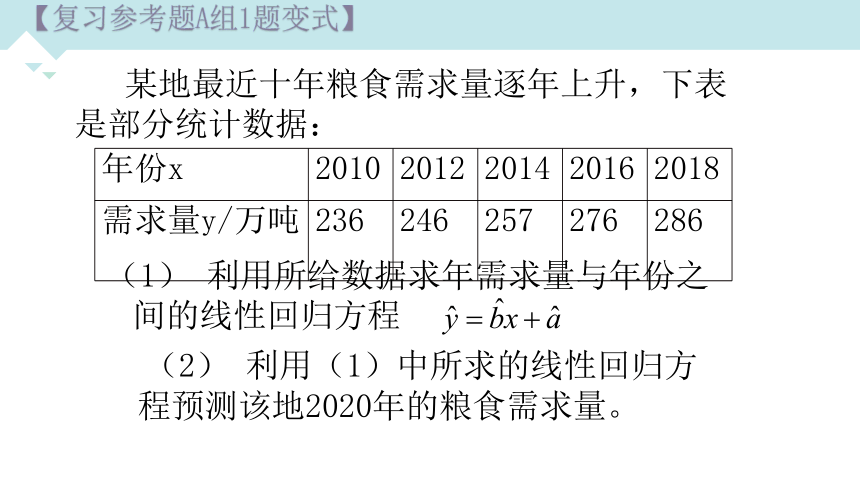
【复习参考题A组1题变式】
某地最近十年粮食需求量逐年上升,下表是部分统计数据:
{5940675A-B579-460E-94D1-54222C63F5DA}年份x
2010
2012
2014
2016
2018
需求量y/万吨
236
246
257
276
286
(1) 利用所给数据求年需求量与年份之间的线性回归方程
(2) 利用(1)中所求的线性回归方程预测该地2020年的粮食需求量。
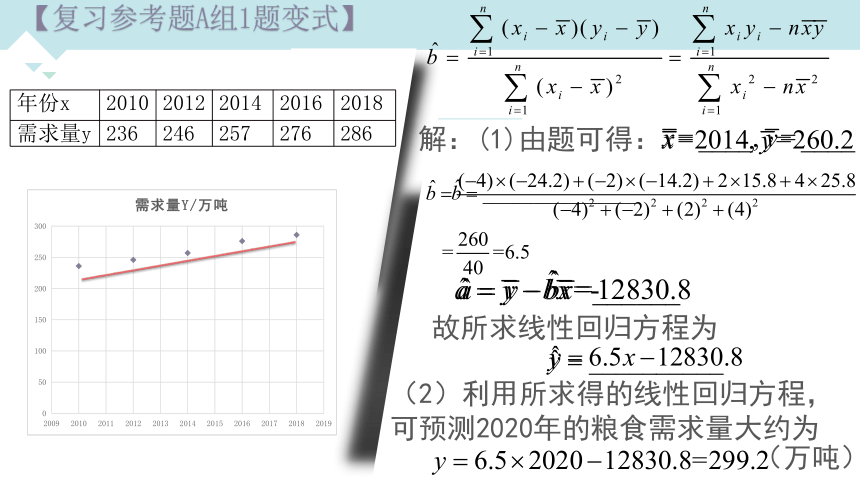
解:(1)由题可得:
【复习参考题A组1题变式】
{5940675A-B579-460E-94D1-54222C63F5DA}年份x
2010
2012
2014
2016
2018
需求量y
236
246
257
276
286
故所求线性回归方程为
(2)利用所求得的线性回归方程,可预测2020年的粮食需求量大约为
(万吨)
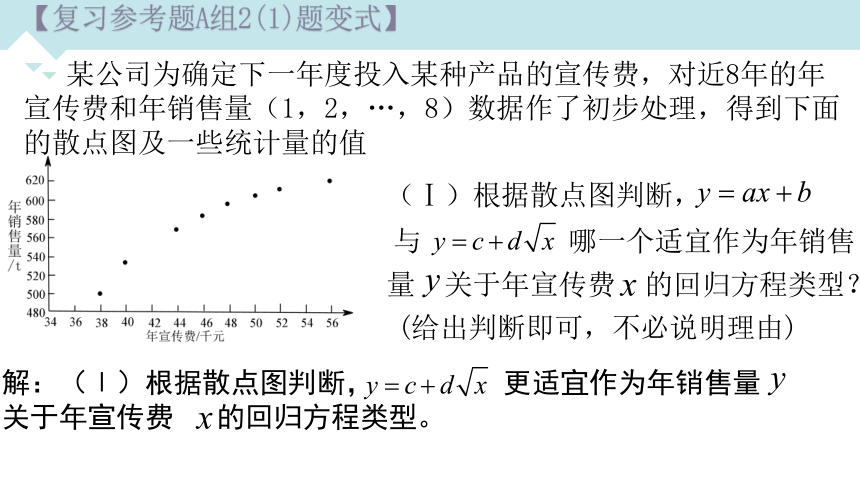
【复习参考题A组2(1)题变式】
某公司为确定下一年度投入某种产品的宣传费,对近8年的年宣传费和年销售量(1,2,…,8)数据作了初步处理,得到下面的散点图及一些统计量的值
(Ⅰ)根据散点图判断,
与
哪一个适宜作为年销售
量 关于年宣传费 的回归方程类型?
(给出判断即可,不必说明理由)
解:(Ⅰ)根据散点图判断, 更适宜作为年销售量 关于年宣传费 的回归方程类型。
一次函数模型:
指数函数模型:
二次函数模型:
反比例函数模型:
对数函数模型:
【复习参考题A组2(1)题变式】
某公司为确定下一年度投入某种产品的宣传费,对近8年的年宣传费和年销售量(1,2,…,8)数据作了初步处理,得到下面的散点图及一些统计量的值(其表中: , )
(Ⅱ)根据(Ⅰ)的判断结果及表中数据,建立 关于 的回归方程;
附:对于一组数据 , ,…, ,其回归直线
的斜率和截距的最小二乘估计分别为:
【复习参考题A组2(1)题变式】
解:(Ⅱ)令 ,先建立 关于 的线性回归方程式
∴建立 关于 的线性回归方程式为
∴ 关于 的线性回归方程式为
非线性回归方程
线性回归方程
由于
【复习参考题A组2(3)题变式】
一只药用昆虫的产卵数 与一定范围内的温度 有关,现收集了该种药用昆虫的6组观测数据如下表:
甲同学用线性回归模型,得到
乙同学用非线性回归模型,得到: ,且
(1)甲乙两个同学用的回归模型相比,哪种的拟合效果更好?这种模型是不是最好的模型?
(2)用拟合效果好的模型预测温度为35℃时,该药用昆虫的产卵数?
【复习参考题A组2(3)题变式】
甲 线性回归模型
乙 非线性回归模型
注:
线性回归模型的残差平方和
解:(1)由所给的数据求得,线
性回归方程:
的相关指数为:
因为 ,所以乙同学的非线性回归方程拟合效果更好。
(2)当温度为35℃时,该药用昆虫的
产卵数约为:
问题:哪种的拟合效果更好?
【复习参考题A组3题】
调查某医院某段时间内婴儿出生的时间和性别的关系,得到下面的数据表,能否在犯错误的概率不超过0.1的前提下认为婴儿性别与出生时间有关系呢?
【解析】根据上表数据得到
等高条形图:
由等高条形图可以初步判断:
婴儿性别与出生时间有关系。
【复习参考题A组3题】
调查某医院某段时间内婴儿出生的时间和性别的关系,得到下面的数据表,能否在犯错误的概率不超过0.1的前提下认为婴儿性别与出生时间有关系呢?
又因为
解:假设婴儿性别与出生时
间没有关系,由列联表中的
数据得出 的观测值
而3.689>2.706,因此在犯错误
概率不超过0.1的前提下认为
“婴儿的性别和出生的时间有
关系”。
1
2
寻找统计方案
3
建构统计模型
4
提取数字特征
课堂小结
5
决策相应方案
确立决策目标
感谢您的观看
Thank you for your download to watch
——复习参考题
回归分析
独立性检验
01
02
知识回顾
1
散点图
通过散点图了解变量关系,非线性转化为线性的,然后用最小二乘法建立回归模型,接着通过分析残差、指标衡量模型的拟合效果
2
非线性线性
3
回归方程
4
问题预测
回归分析
01
1
列联表
2
假设变量无关
3
随机变量
4
问题决策
独立性检验
02
【复习参考题A组1题变式】
某地最近十年粮食需求量逐年上升,下表是部分统计数据:
{5940675A-B579-460E-94D1-54222C63F5DA}年份x
2010
2012
2014
2016
2018
需求量y/万吨
236
246
257
276
286
(1) 利用所给数据求年需求量与年份之间的线性回归方程
(2) 利用(1)中所求的线性回归方程预测该地2020年的粮食需求量。
解:(1)由题可得:
【复习参考题A组1题变式】
{5940675A-B579-460E-94D1-54222C63F5DA}年份x
2010
2012
2014
2016
2018
需求量y
236
246
257
276
286
故所求线性回归方程为
(2)利用所求得的线性回归方程,可预测2020年的粮食需求量大约为
(万吨)
【复习参考题A组2(1)题变式】
某公司为确定下一年度投入某种产品的宣传费,对近8年的年宣传费和年销售量(1,2,…,8)数据作了初步处理,得到下面的散点图及一些统计量的值
(Ⅰ)根据散点图判断,
与
哪一个适宜作为年销售
量 关于年宣传费 的回归方程类型?
(给出判断即可,不必说明理由)
解:(Ⅰ)根据散点图判断, 更适宜作为年销售量 关于年宣传费 的回归方程类型。
一次函数模型:
指数函数模型:
二次函数模型:
反比例函数模型:
对数函数模型:
【复习参考题A组2(1)题变式】
某公司为确定下一年度投入某种产品的宣传费,对近8年的年宣传费和年销售量(1,2,…,8)数据作了初步处理,得到下面的散点图及一些统计量的值(其表中: , )
(Ⅱ)根据(Ⅰ)的判断结果及表中数据,建立 关于 的回归方程;
附:对于一组数据 , ,…, ,其回归直线
的斜率和截距的最小二乘估计分别为:
【复习参考题A组2(1)题变式】
解:(Ⅱ)令 ,先建立 关于 的线性回归方程式
∴建立 关于 的线性回归方程式为
∴ 关于 的线性回归方程式为
非线性回归方程
线性回归方程
由于
【复习参考题A组2(3)题变式】
一只药用昆虫的产卵数 与一定范围内的温度 有关,现收集了该种药用昆虫的6组观测数据如下表:
甲同学用线性回归模型,得到
乙同学用非线性回归模型,得到: ,且
(1)甲乙两个同学用的回归模型相比,哪种的拟合效果更好?这种模型是不是最好的模型?
(2)用拟合效果好的模型预测温度为35℃时,该药用昆虫的产卵数?
【复习参考题A组2(3)题变式】
甲 线性回归模型
乙 非线性回归模型
注:
线性回归模型的残差平方和
解:(1)由所给的数据求得,线
性回归方程:
的相关指数为:
因为 ,所以乙同学的非线性回归方程拟合效果更好。
(2)当温度为35℃时,该药用昆虫的
产卵数约为:
问题:哪种的拟合效果更好?
【复习参考题A组3题】
调查某医院某段时间内婴儿出生的时间和性别的关系,得到下面的数据表,能否在犯错误的概率不超过0.1的前提下认为婴儿性别与出生时间有关系呢?
【解析】根据上表数据得到
等高条形图:
由等高条形图可以初步判断:
婴儿性别与出生时间有关系。
【复习参考题A组3题】
调查某医院某段时间内婴儿出生的时间和性别的关系,得到下面的数据表,能否在犯错误的概率不超过0.1的前提下认为婴儿性别与出生时间有关系呢?
又因为
解:假设婴儿性别与出生时
间没有关系,由列联表中的
数据得出 的观测值
而3.689>2.706,因此在犯错误
概率不超过0.1的前提下认为
“婴儿的性别和出生的时间有
关系”。
1
2
寻找统计方案
3
建构统计模型
4
提取数字特征
课堂小结
5
决策相应方案
确立决策目标
感谢您的观看
Thank you for your download to watch
