1.3.1 正弦函数的图象与性质 课件(共18张PPT)——2020-2021学年高一人教B版必修4 第一章基本初等函数(II )
文档属性
| 名称 | 1.3.1 正弦函数的图象与性质 课件(共18张PPT)——2020-2021学年高一人教B版必修4 第一章基本初等函数(II ) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-01 09:20:30 | ||
图片预览

文档简介
(共18张PPT)
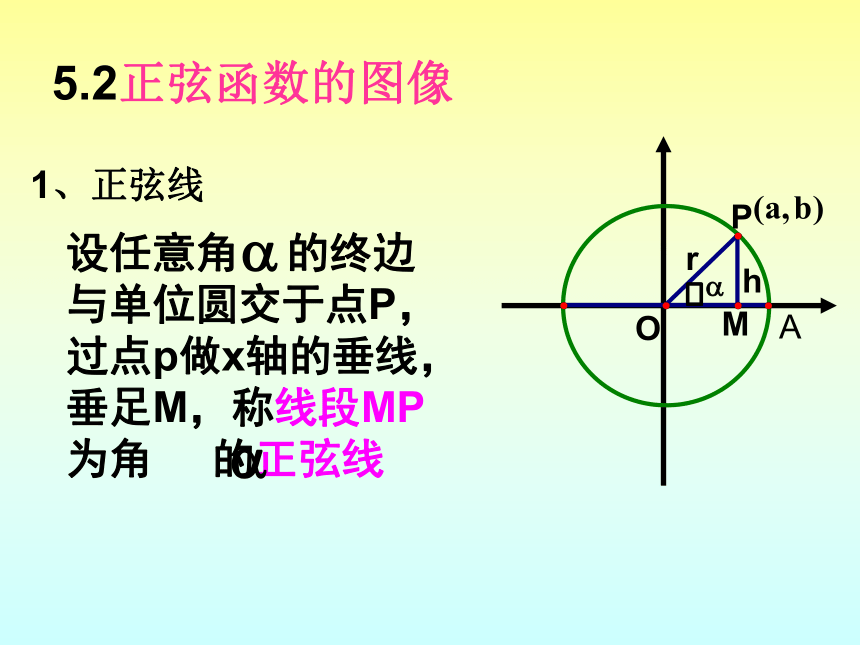
5.2正弦函数的图像
1、正弦线
设任意角
的终边与单位圆交于点P,过点p做x轴的垂线,垂足M,称线段MP为角
的正弦线
1
-1
1
-1
o
P(u,v)
M
x
y
α
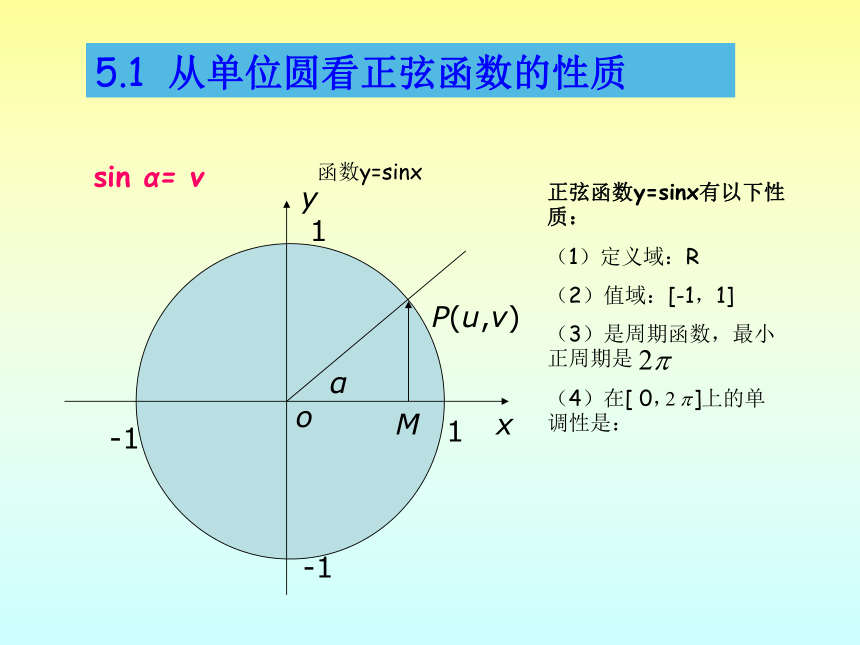
正弦函数y=sinx有以下性质:
(1)定义域:R
(2)值域:[-1,1]
(3)是周期函数,最小正周期是
(4)在[
0,
]上的单调性是:
5.1
从单位圆看正弦函数的性质
sin
α=
v
函数y=sinx
1
-1
0
y
x
●
●
●
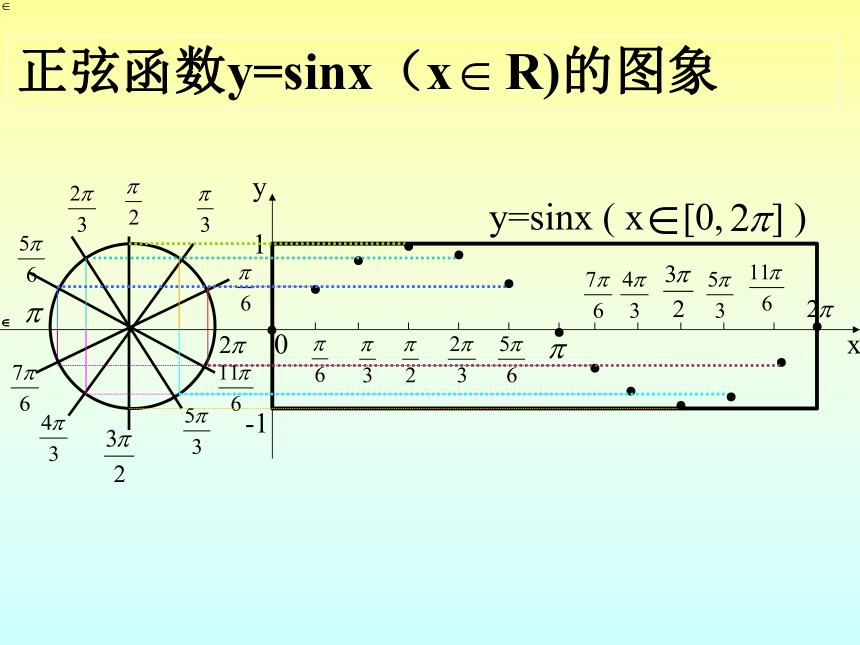
正弦函数y=sinx(x
R)的图象
y=sinx
(
x
[0,
]
)
●
●
●
●
●
●
●
●
●
●
y=sin
x,
x∈R
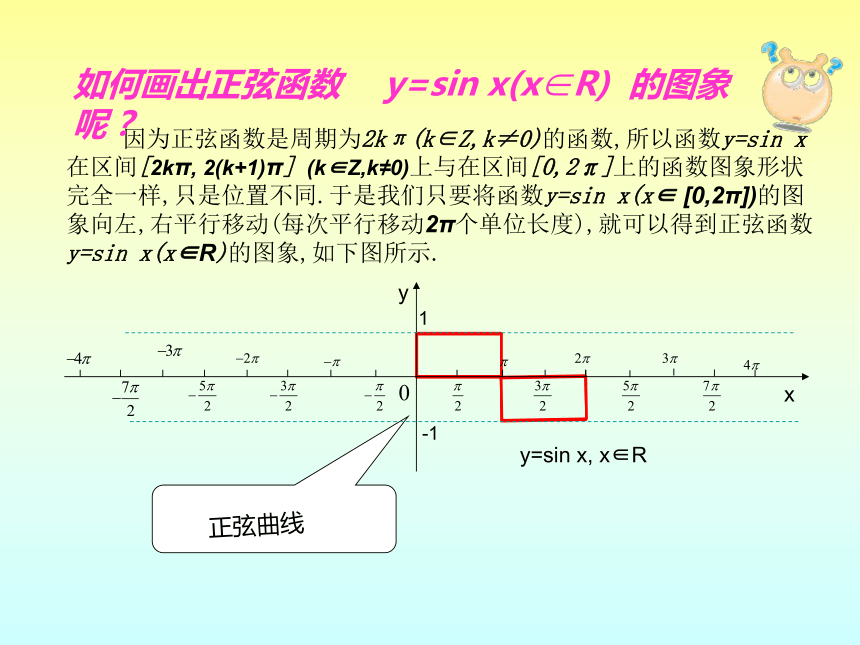
因为正弦函数是周期为2kπ(k∈Z,k≠0)的函数,所以函数y=sin
x在区间[2kπ,
2(k+1)π]
(k∈Z,k≠0)上与在区间[0,2π]上的函数图象形状完全一样,只是位置不同.于是我们只要将函数y=sin
x(x∈
[0,2π])的图象向左,右平行移动(每次平行移动2π个单位长度),就可以得到正弦函数y=sin
x(x∈R)的图象,如下图所示.
正弦曲线
x
y
1
-1
如何画出正弦函数
y=sin
x(x∈R)
的图象呢?
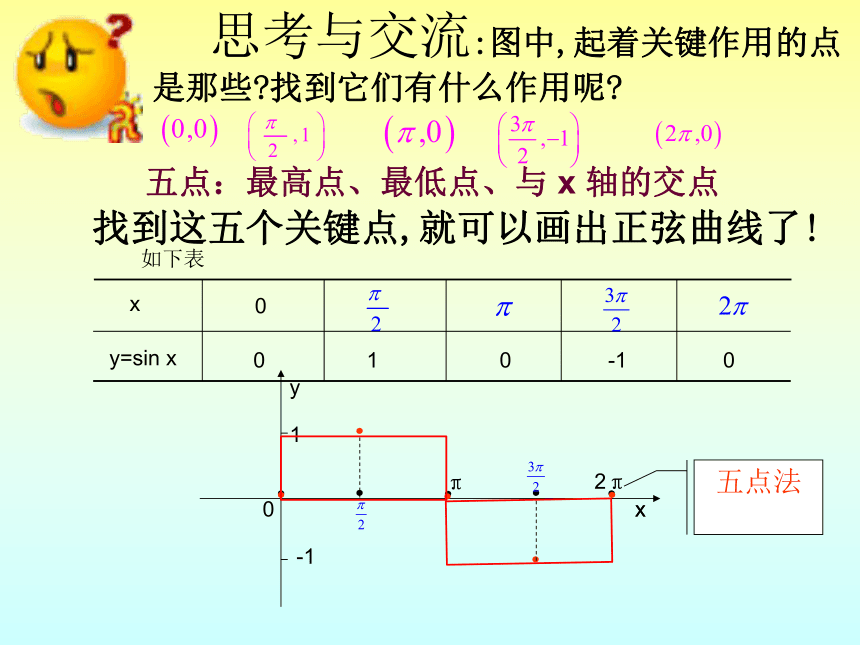
思考与交流:图中,起着关键作用的点是那些?找到它们有什么作用呢?
找到这五个关键点,就可以画出正弦曲线了!
如下表
x
y=sin
x
0
0
1
0
-1
0
.
.
.
.
x
y
0
π
.
2π
1
-1
x
.
.
.
.
.
五点法
五点:最高点、最低点、与
x
轴的交点
x
y=sin
x
y=-sin
x
0
0
1
0
-1
0
0
-1
0
1
0
.
.
.
.
x
y
0
π
.
2π
1
-1
x
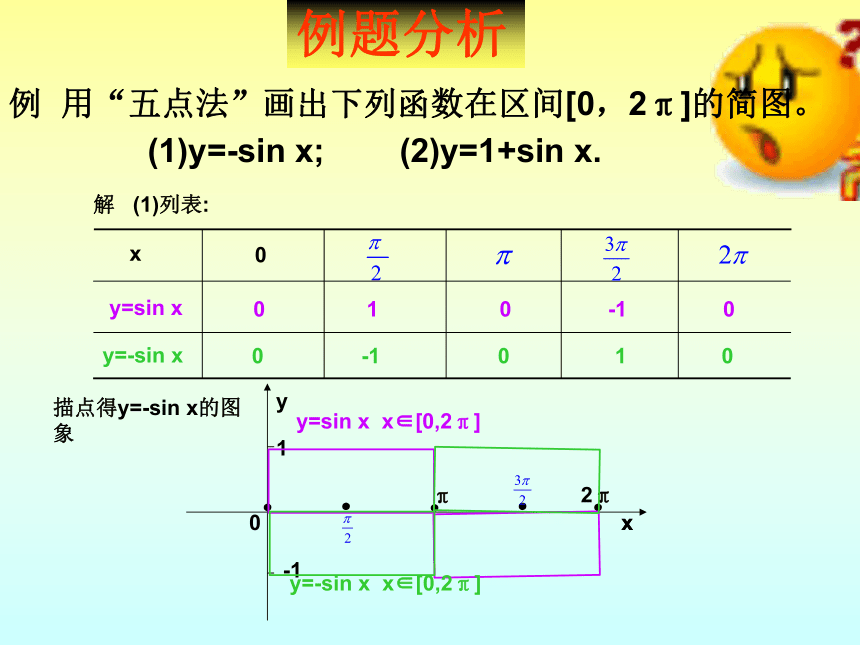
描点得y=-sin
x的图象
y=sin
x
x∈[0,2π]
y=-sin
x
x∈[0,2π]
例
用“五点法”画出下列函数在区间[0,2π]的简图。
(1)y=-sin
x;
(2)y=1+sin
x.
解
(1)列表:
例题分析
x
y=sin
x
y=1+sin
x
0
0
1
0
-1
0
1
2
1
0
1
(2)
列表:
描点得y=1+sin
x的图象
.
.
.
.
x
y
0
π
.
2π
1
-1
x
y=sin
x
x∈[0,2π]
y=1+sin
x
x∈[0,2π]
用“五点法”画出下列函数在区间[0,2π]的图。
(1)y=2+sin
x;
(2)y=sin
x-1;
(3)y=3sin
x.
y=sin
x
-1
x∈[0,2π]
y=sin
3x
x∈[0,2π]
y=2+sin
x
x∈[0,2π]
.
.
.
.
x
y
0
π
.
2π
1
-1
x
2
3
练习小结
小结:
作正弦函数图象的简图的方法是:
作业:P28
2
“五点法”
正弦函数的性质
正弦函数y=sinx的性质:
sin(x+2kπ)=sin
x,
(k∈Z),
(3)周期性
当x=________________时,
当x=________________时, 值域是:
(2)值域
(1)定义域
(5)单调性
(6)奇偶性
是______函数,图象关于_______对称
(4)最大值与最小值
正弦函数y=sinx的性质:
定义域
R
值域
[-1,1]
奇偶性
奇函数
周期性
2π
单调性
最值
正弦函数的性质
1
求函数y=2+sinx的最大值、最小值和周期,并求这个函数取最大值、最小值的x值的集合。
解:
使y=2+sinx取得最大值的x的集合是:
使y=2+sinx取得最小值的x的集合是:
周期
2
不求值,比较下列各对正弦值的大小:
(1) (2)
解:(1)
且y=sinx在
上是增函数,
(2)
且y=sinx在
上是减函数,
3
求y=
5+sinx这个函数的最大值、最小值和周期,并求这个函数分别取得最大值及最小值的x的集合。
使y=
5+sinx取得最大值的x的集合是:
使y=
5+sinx取得最小值的x的集合是:
解:
4
不求值,比较下列各对正弦值的大小:
(1)
(2)
解:(1)
作业
28页
5.2正弦函数的图像
1、正弦线
设任意角
的终边与单位圆交于点P,过点p做x轴的垂线,垂足M,称线段MP为角
的正弦线
1
-1
1
-1
o
P(u,v)
M
x
y
α
正弦函数y=sinx有以下性质:
(1)定义域:R
(2)值域:[-1,1]
(3)是周期函数,最小正周期是
(4)在[
0,
]上的单调性是:
5.1
从单位圆看正弦函数的性质
sin
α=
v
函数y=sinx
1
-1
0
y
x
●
●
●
正弦函数y=sinx(x
R)的图象
y=sinx
(
x
[0,
]
)
●
●
●
●
●
●
●
●
●
●
y=sin
x,
x∈R
因为正弦函数是周期为2kπ(k∈Z,k≠0)的函数,所以函数y=sin
x在区间[2kπ,
2(k+1)π]
(k∈Z,k≠0)上与在区间[0,2π]上的函数图象形状完全一样,只是位置不同.于是我们只要将函数y=sin
x(x∈
[0,2π])的图象向左,右平行移动(每次平行移动2π个单位长度),就可以得到正弦函数y=sin
x(x∈R)的图象,如下图所示.
正弦曲线
x
y
1
-1
如何画出正弦函数
y=sin
x(x∈R)
的图象呢?
思考与交流:图中,起着关键作用的点是那些?找到它们有什么作用呢?
找到这五个关键点,就可以画出正弦曲线了!
如下表
x
y=sin
x
0
0
1
0
-1
0
.
.
.
.
x
y
0
π
.
2π
1
-1
x
.
.
.
.
.
五点法
五点:最高点、最低点、与
x
轴的交点
x
y=sin
x
y=-sin
x
0
0
1
0
-1
0
0
-1
0
1
0
.
.
.
.
x
y
0
π
.
2π
1
-1
x
描点得y=-sin
x的图象
y=sin
x
x∈[0,2π]
y=-sin
x
x∈[0,2π]
例
用“五点法”画出下列函数在区间[0,2π]的简图。
(1)y=-sin
x;
(2)y=1+sin
x.
解
(1)列表:
例题分析
x
y=sin
x
y=1+sin
x
0
0
1
0
-1
0
1
2
1
0
1
(2)
列表:
描点得y=1+sin
x的图象
.
.
.
.
x
y
0
π
.
2π
1
-1
x
y=sin
x
x∈[0,2π]
y=1+sin
x
x∈[0,2π]
用“五点法”画出下列函数在区间[0,2π]的图。
(1)y=2+sin
x;
(2)y=sin
x-1;
(3)y=3sin
x.
y=sin
x
-1
x∈[0,2π]
y=sin
3x
x∈[0,2π]
y=2+sin
x
x∈[0,2π]
.
.
.
.
x
y
0
π
.
2π
1
-1
x
2
3
练习小结
小结:
作正弦函数图象的简图的方法是:
作业:P28
2
“五点法”
正弦函数的性质
正弦函数y=sinx的性质:
sin(x+2kπ)=sin
x,
(k∈Z),
(3)周期性
当x=________________时,
当x=________________时, 值域是:
(2)值域
(1)定义域
(5)单调性
(6)奇偶性
是______函数,图象关于_______对称
(4)最大值与最小值
正弦函数y=sinx的性质:
定义域
R
值域
[-1,1]
奇偶性
奇函数
周期性
2π
单调性
最值
正弦函数的性质
1
求函数y=2+sinx的最大值、最小值和周期,并求这个函数取最大值、最小值的x值的集合。
解:
使y=2+sinx取得最大值的x的集合是:
使y=2+sinx取得最小值的x的集合是:
周期
2
不求值,比较下列各对正弦值的大小:
(1) (2)
解:(1)
且y=sinx在
上是增函数,
(2)
且y=sinx在
上是减函数,
3
求y=
5+sinx这个函数的最大值、最小值和周期,并求这个函数分别取得最大值及最小值的x的集合。
使y=
5+sinx取得最大值的x的集合是:
使y=
5+sinx取得最小值的x的集合是:
解:
4
不求值,比较下列各对正弦值的大小:
(1)
(2)
解:(1)
作业
28页
