_1.3.1 正弦函数的图象与性质 课件(共19张PPT)2020-2021学年高中数学人教B版必修4
文档属性
| 名称 | _1.3.1 正弦函数的图象与性质 课件(共19张PPT)2020-2021学年高中数学人教B版必修4 |

|
|
| 格式 | ppt | ||
| 文件大小 | 796.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-01 09:21:38 | ||
图片预览




文档简介
(共19张PPT)
教学目标:
1、掌握利用正切线画正切函数图象
的方法;
2、能够利用正切函数图象准确归纳其性质并能简单地应用。
学习重点:
正切函数的图象及其主要性质.
学习难点:
利用正切线画出
的图象.
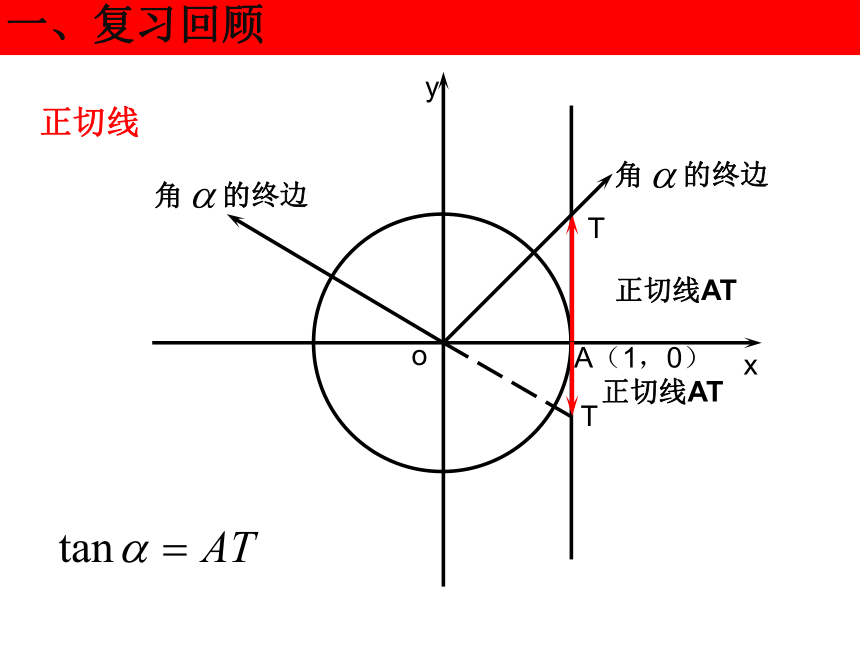
A(1,0)
T
y
o
x
T
的终边
角
的终边
角
正切线AT
正切线AT
一、复习回顾
正切线
二、知识探究
思考1:正切函数的定义域是什么?
正切函数是周期函数,周期是π.
正切函数
是否为周期函数?
思考2:
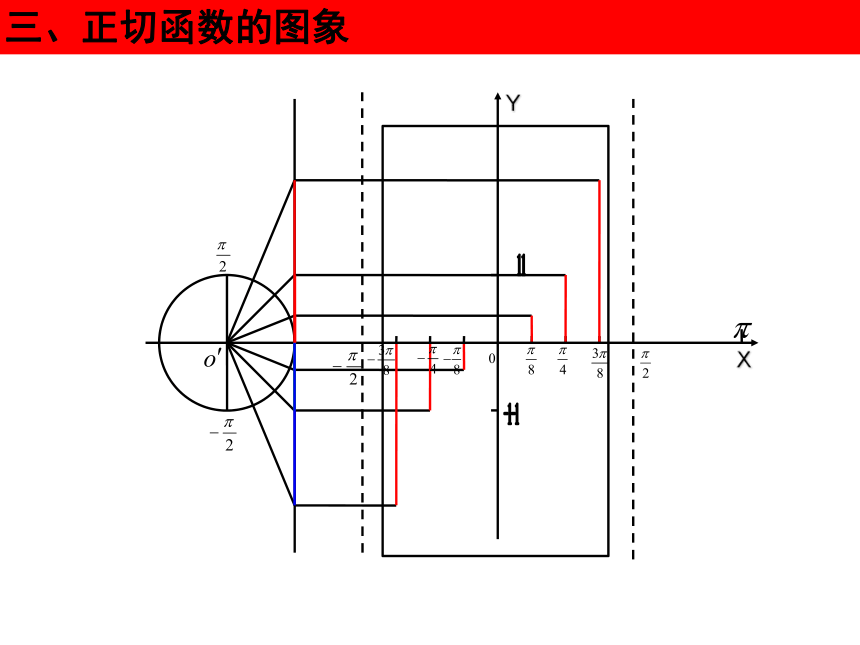
三、正切函数的图象
X
Y
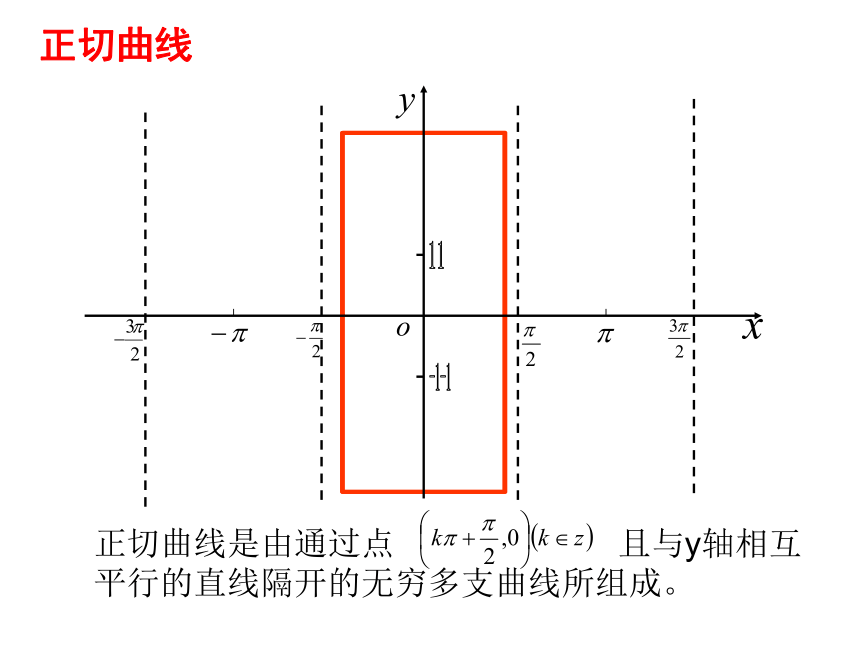
正切曲线
正切曲线是由通过点
且与y轴相互平行的直线隔开的无穷多支曲线所组成。
四、观察正切函数的图象,归纳其性质:
y
x
1
-1
?/2
-?/2
?
3?/2
-3?/2
-?
0
思考1:正切函数在整个定义域上是不是增函数?
(1)正切函数在整个定义域上不具有单调性,因为它的定义域不连续,所以不能说它在整个定义域内是增函数;
(2)正切函数在每个单调区间内是增函数。
思考2:一条平行于x轴的直线与正切曲线相邻两支的交点的距离为多少?
一个周期π
例1
求函数
的定义域
那么函数
的定义域是:
所以由 可得:
所以函数
的定义域是:
解:令
求函数
的定义域
练一练
题型探究:
例2
求函数
的周期
题型探究:
练一练
解:
例3
比较下列正切函数值的大小
与
解:
在
上是增函数
又
利用单调性
题型探究:
练一练
y
x
1
-1
?
-?
0
例4 求下列函数的单调区间:
灵活应用:
题型探究:
练一练
思考:如何求y=Atan(ωx+Ф)的单调区间?
当堂检测
1.函数y=tan
(2x+
)的周期是
(
)
(A)
π
(B)
2π
(C)
(D)
C
2.已知a=tan1,
b=tan2,
c=tan3,
则a、b、c的大小关系是
(
)
(A)
a(B)
c(C)
b(D)
bC
基础训练
C
4.
函数y=2tan(
)的定义域是_________.
定义域是(2kπ-
,
2kπ+
)(k∈Z)
5.函数y=tan(
)的递增区间是__________.
6.函数
的定义域是(
)
(A)
{x|kπ,
k∈Z}
(B)
{x|2kπk∈Z}
(C)
{x|kπ,
k∈Z}
(D)
第一、三象限
C
能力提升
(1)正切函数的图象
(2)正切函数的性质:
定义域:
值域:
周期性:
奇偶性:
单调性:
全体实数R
正切函数是周期函数,
最小正周期是
奇函数
正切函数在开区间
内都是增函数。
自我小结
教学目标:
1、掌握利用正切线画正切函数图象
的方法;
2、能够利用正切函数图象准确归纳其性质并能简单地应用。
学习重点:
正切函数的图象及其主要性质.
学习难点:
利用正切线画出
的图象.
A(1,0)
T
y
o
x
T
的终边
角
的终边
角
正切线AT
正切线AT
一、复习回顾
正切线
二、知识探究
思考1:正切函数的定义域是什么?
正切函数是周期函数,周期是π.
正切函数
是否为周期函数?
思考2:
三、正切函数的图象
X
Y
正切曲线
正切曲线是由通过点
且与y轴相互平行的直线隔开的无穷多支曲线所组成。
四、观察正切函数的图象,归纳其性质:
y
x
1
-1
?/2
-?/2
?
3?/2
-3?/2
-?
0
思考1:正切函数在整个定义域上是不是增函数?
(1)正切函数在整个定义域上不具有单调性,因为它的定义域不连续,所以不能说它在整个定义域内是增函数;
(2)正切函数在每个单调区间内是增函数。
思考2:一条平行于x轴的直线与正切曲线相邻两支的交点的距离为多少?
一个周期π
例1
求函数
的定义域
那么函数
的定义域是:
所以由 可得:
所以函数
的定义域是:
解:令
求函数
的定义域
练一练
题型探究:
例2
求函数
的周期
题型探究:
练一练
解:
例3
比较下列正切函数值的大小
与
解:
在
上是增函数
又
利用单调性
题型探究:
练一练
y
x
1
-1
?
-?
0
例4 求下列函数的单调区间:
灵活应用:
题型探究:
练一练
思考:如何求y=Atan(ωx+Ф)的单调区间?
当堂检测
1.函数y=tan
(2x+
)的周期是
(
)
(A)
π
(B)
2π
(C)
(D)
C
2.已知a=tan1,
b=tan2,
c=tan3,
则a、b、c的大小关系是
(
)
(A)
a
c
b
b
基础训练
C
4.
函数y=2tan(
)的定义域是_________.
定义域是(2kπ-
,
2kπ+
)(k∈Z)
5.函数y=tan(
)的递增区间是__________.
6.函数
的定义域是(
)
(A)
{x|kπ
k∈Z}
(B)
{x|2kπ
(C)
{x|kπ
k∈Z}
(D)
第一、三象限
C
能力提升
(1)正切函数的图象
(2)正切函数的性质:
定义域:
值域:
周期性:
奇偶性:
单调性:
全体实数R
正切函数是周期函数,
最小正周期是
奇函数
正切函数在开区间
内都是增函数。
自我小结
