_1.2.3 同角三角函数的基本关系式课件(共21张PPT)2020-2021学年高中数学人教B版必修4
文档属性
| 名称 | _1.2.3 同角三角函数的基本关系式课件(共21张PPT)2020-2021学年高中数学人教B版必修4 |

|
|
| 格式 | ppt | ||
| 文件大小 | 681.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-01 09:23:07 | ||
图片预览







文档简介
(共21张PPT)
1.2.3 同角三角函数的基本关系式
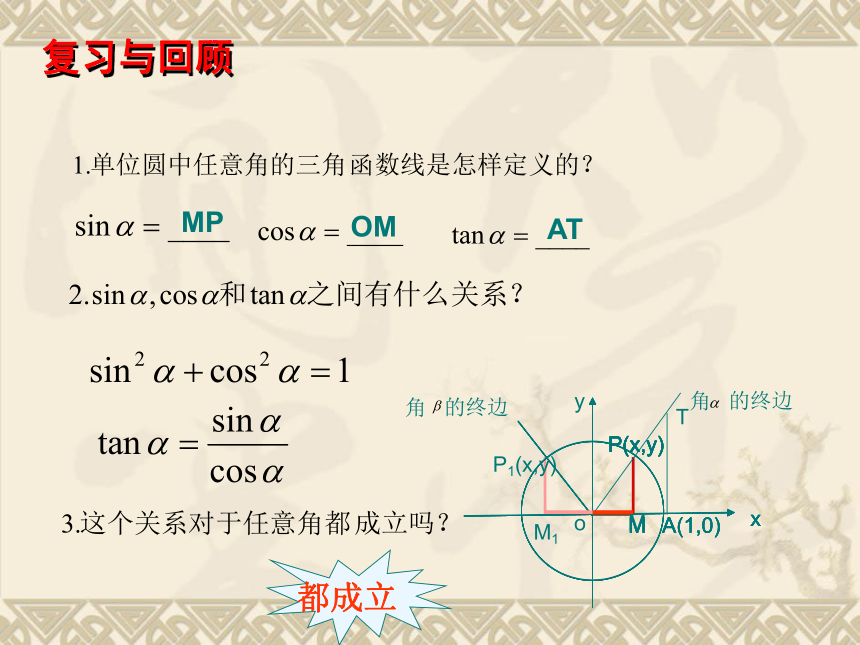
复习与回顾
T
M
P1(x,y)
M
M
M
y
x
o
M
M1
A(1,0)
P(x,y)
P(x,y)
P(x,y)
P(x,y)
P(x,y)
A(1,0)
P(x,y)
角
的终边
角
的终边
x
A(1,0)
x
P(x,y)
A(1,0)
x
OM
MP
AT
都成立
同角三角函数基本关系式:
公式的本质解读
1.“同角”的概念与角的表达形式无关,其含义是角相同。
2.两种关系式(公式)都必须在定义域允许的范围内成立.
平方关系:
商数关系:
平方关系:
商数关系:
平方关系:
平方关系:
基本变形
思考1:对于平方关系
可作哪些变形?
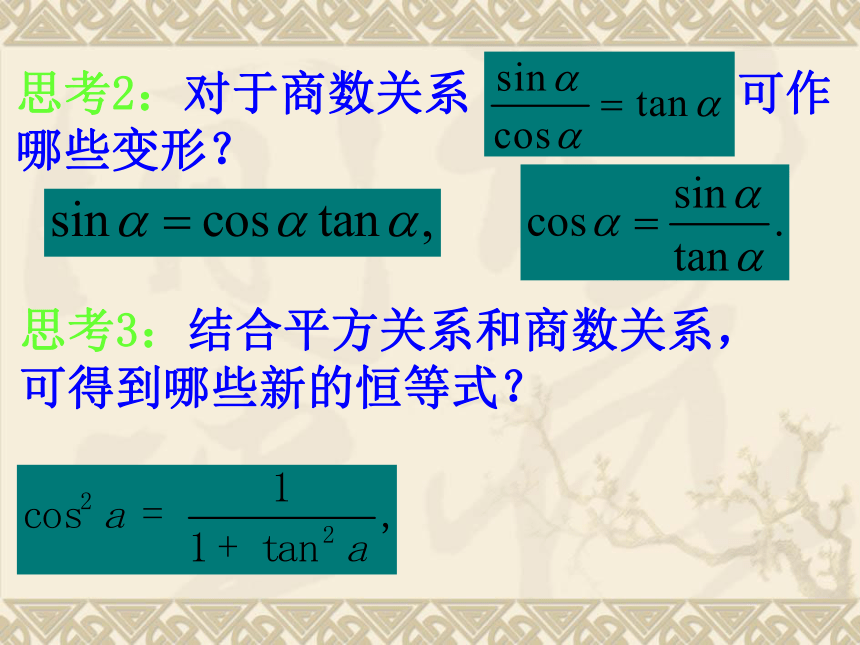
思考2:对于商数关系
可作哪些变形?
思考3:结合平方关系和商数关系,可得到哪些新的恒等式?
由
得
解:
应用举例
从而
解:因为
,
所以
是第
一或第二象限角.
由
得
当
是第一象限角,那么
当
是第二象限角,那么
方法一:
应用举例
解:由题意和基本三角恒等式,列出方程组
方法二:
②
①
应用举例
解:依题意和基本三角恒等式,得到方程组
应用举例
应用举例
弦化切
应用举例
应用举例
解
应用举例
化简的一般要求:三角函数种数尽量少;项数尽量少;次数尽量低;尽量使分母不含三角函数式;尽量使被开方数不含三角函数式;能求出值的应尽量求出值.
依据三角函数式的结构特点,常采用的变换方法:异角化同角;异名化同名;异次化同次;高次化降次
例5:化简
切化弦
应用举例
例5.化简
变式:化简
例6.化简
变式:化简
变式:化简
点评:涉及公式
A
B
D
达标测试:
达标测试:
达标测试:
解:因为
1、掌握同角三角函数基本关系式并牢记.
2、应用(1)求值
同角三角函数的基本关系式
3、数学思想:
小
结
①应用公式(重点)
②列方程组
分类讨论,
(2)化简
方程思想,
变量归一的思想
作业:
P25练习A
1、2、4
1.2.3 同角三角函数的基本关系式
复习与回顾
T
M
P1(x,y)
M
M
M
y
x
o
M
M1
A(1,0)
P(x,y)
P(x,y)
P(x,y)
P(x,y)
P(x,y)
A(1,0)
P(x,y)
角
的终边
角
的终边
x
A(1,0)
x
P(x,y)
A(1,0)
x
OM
MP
AT
都成立
同角三角函数基本关系式:
公式的本质解读
1.“同角”的概念与角的表达形式无关,其含义是角相同。
2.两种关系式(公式)都必须在定义域允许的范围内成立.
平方关系:
商数关系:
平方关系:
商数关系:
平方关系:
平方关系:
基本变形
思考1:对于平方关系
可作哪些变形?
思考2:对于商数关系
可作哪些变形?
思考3:结合平方关系和商数关系,可得到哪些新的恒等式?
由
得
解:
应用举例
从而
解:因为
,
所以
是第
一或第二象限角.
由
得
当
是第一象限角,那么
当
是第二象限角,那么
方法一:
应用举例
解:由题意和基本三角恒等式,列出方程组
方法二:
②
①
应用举例
解:依题意和基本三角恒等式,得到方程组
应用举例
应用举例
弦化切
应用举例
应用举例
解
应用举例
化简的一般要求:三角函数种数尽量少;项数尽量少;次数尽量低;尽量使分母不含三角函数式;尽量使被开方数不含三角函数式;能求出值的应尽量求出值.
依据三角函数式的结构特点,常采用的变换方法:异角化同角;异名化同名;异次化同次;高次化降次
例5:化简
切化弦
应用举例
例5.化简
变式:化简
例6.化简
变式:化简
变式:化简
点评:涉及公式
A
B
D
达标测试:
达标测试:
达标测试:
解:因为
1、掌握同角三角函数基本关系式并牢记.
2、应用(1)求值
同角三角函数的基本关系式
3、数学思想:
小
结
①应用公式(重点)
②列方程组
分类讨论,
(2)化简
方程思想,
变量归一的思想
作业:
P25练习A
1、2、4
