_ 2.2.3 用平面向量坐标表示向量共线条件 课件(共13张PPT)2020-2021学年高中数学人教B版必修4
文档属性
| 名称 | _ 2.2.3 用平面向量坐标表示向量共线条件 课件(共13张PPT)2020-2021学年高中数学人教B版必修4 |

|
|
| 格式 | ppt | ||
| 文件大小 | 541.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-01 09:24:16 | ||
图片预览





文档简介
(共13张PPT)
高一数学必修四人教B版
2.2.3用平面向量坐标
表示向量共线条件
1.理解用坐标表示的平面向量共线的条件.
2.能根据平面向量的坐标,判断向量是否
共线.
3.掌握三点共线的判断方法.
学习目标
2.向量共线的条件?
平行向量基本定理:
表示此向量的有向线段的
终点坐标减去起点坐标.
1.向量的坐标?
向量
与非零向量
平行(共线),当且仅当
存在唯一实数
,
使得
复习回顾
O
x
y
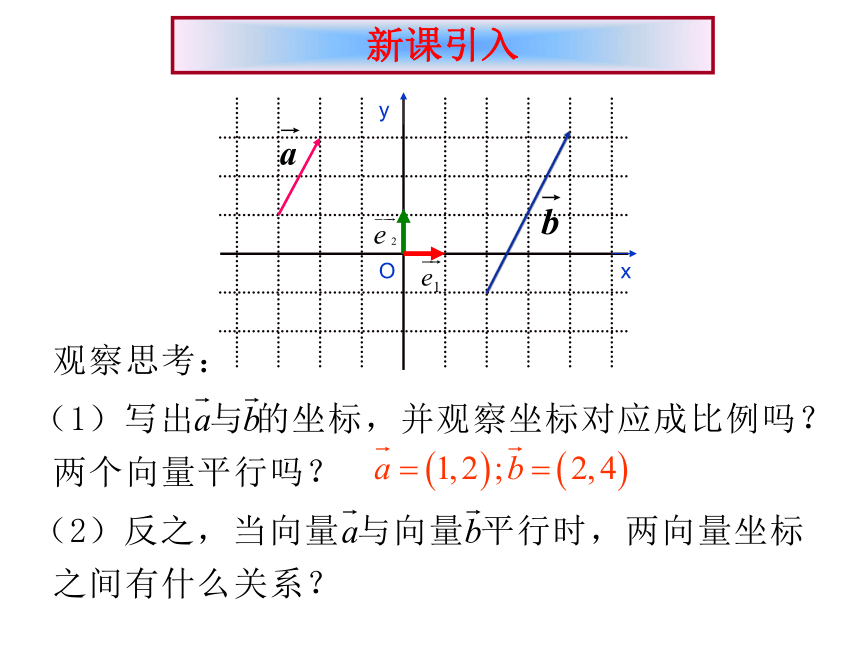
新课引入
平面向量共线的坐标表示
设
有
(1)(2)两式两边分别乘以
可得
即
如果
平面向量共线的坐标表示
反之也成立。
(3)-(4)可得
两个平面向量共线的坐标表示:
语言表述:
两个向量平行的条件是相应坐标成比例
平面向量共线的条件
此外,当向量
不平行于坐标轴时,即b1≠0,b2≠0时,有
例1.
已知向量
=(2,5)和向量
=(1,y),并且向量
,求向量
的纵坐标y。
解:因为
所以
2×y
-
5×1=0
解得
题型1.向量共线
典例精析
例2.
在直角坐标系xOy内,已知A(-2,-3),
B(0,1),C(2,5),
求证:A、B、C三点共线.
题型2.三点共线
证明:
所以
因此A,B,C三点共线.
因为
2×8-4×4
=0
1.已知
=(-3,
9),
=(2,
y),且
,求y.
解:-3y-9×2=0
y
=-6
解:3sinα-4
cosα=0
tanα=4
/3
2.已知
=(3,
4),
=(cosα,
sinα),
且
,
求tanα.
课堂练习
3.已知
=(1,
0),
=(2,
1),
当实数k为何
值时,向量
与
平行?
并确定它们是同向还是反向.
因此,两个向量反向.
解:
所以(k-2)×3-(-1)×7=0
1.
向量平行(共线)的表示形式:
小
结
2.
运用向量的坐标形式研究向量
共线及几何中的三点共线问题
作
业
谢谢,再见!
高一数学必修四人教B版
2.2.3用平面向量坐标
表示向量共线条件
1.理解用坐标表示的平面向量共线的条件.
2.能根据平面向量的坐标,判断向量是否
共线.
3.掌握三点共线的判断方法.
学习目标
2.向量共线的条件?
平行向量基本定理:
表示此向量的有向线段的
终点坐标减去起点坐标.
1.向量的坐标?
向量
与非零向量
平行(共线),当且仅当
存在唯一实数
,
使得
复习回顾
O
x
y
新课引入
平面向量共线的坐标表示
设
有
(1)(2)两式两边分别乘以
可得
即
如果
平面向量共线的坐标表示
反之也成立。
(3)-(4)可得
两个平面向量共线的坐标表示:
语言表述:
两个向量平行的条件是相应坐标成比例
平面向量共线的条件
此外,当向量
不平行于坐标轴时,即b1≠0,b2≠0时,有
例1.
已知向量
=(2,5)和向量
=(1,y),并且向量
,求向量
的纵坐标y。
解:因为
所以
2×y
-
5×1=0
解得
题型1.向量共线
典例精析
例2.
在直角坐标系xOy内,已知A(-2,-3),
B(0,1),C(2,5),
求证:A、B、C三点共线.
题型2.三点共线
证明:
所以
因此A,B,C三点共线.
因为
2×8-4×4
=0
1.已知
=(-3,
9),
=(2,
y),且
,求y.
解:-3y-9×2=0
y
=-6
解:3sinα-4
cosα=0
tanα=4
/3
2.已知
=(3,
4),
=(cosα,
sinα),
且
,
求tanα.
课堂练习
3.已知
=(1,
0),
=(2,
1),
当实数k为何
值时,向量
与
平行?
并确定它们是同向还是反向.
因此,两个向量反向.
解:
所以(k-2)×3-(-1)×7=0
1.
向量平行(共线)的表示形式:
小
结
2.
运用向量的坐标形式研究向量
共线及几何中的三点共线问题
作
业
谢谢,再见!
