_1.4.1 正弦函数、余弦函数的图象 课件(19张)——2020-2021学年高一下学期人教A版必修4第一章三角函数
文档属性
| 名称 | _1.4.1 正弦函数、余弦函数的图象 课件(19张)——2020-2021学年高一下学期人教A版必修4第一章三角函数 |

|
|
| 格式 | ppt | ||
| 文件大小 | 2.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-01 00:00:00 | ||
图片预览

文档简介
(共19张PPT)
1.4.1正弦函数、余弦函数的图象
授课人:
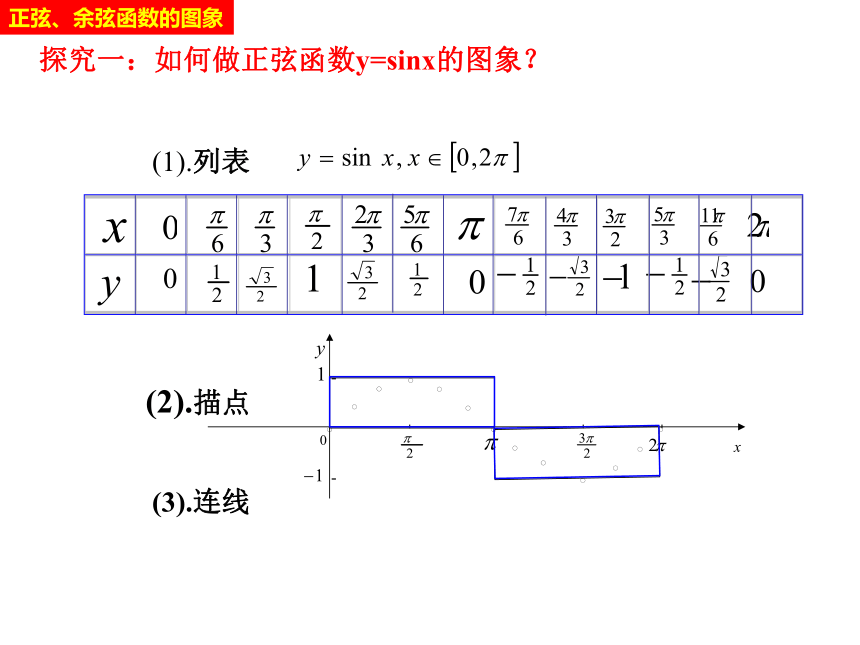
(1).列表
(3).连线
-
-
-
-
-
-
探究一:如何做正弦函数y=sinx的图象?
正弦、余弦函数的图象
(2).描点
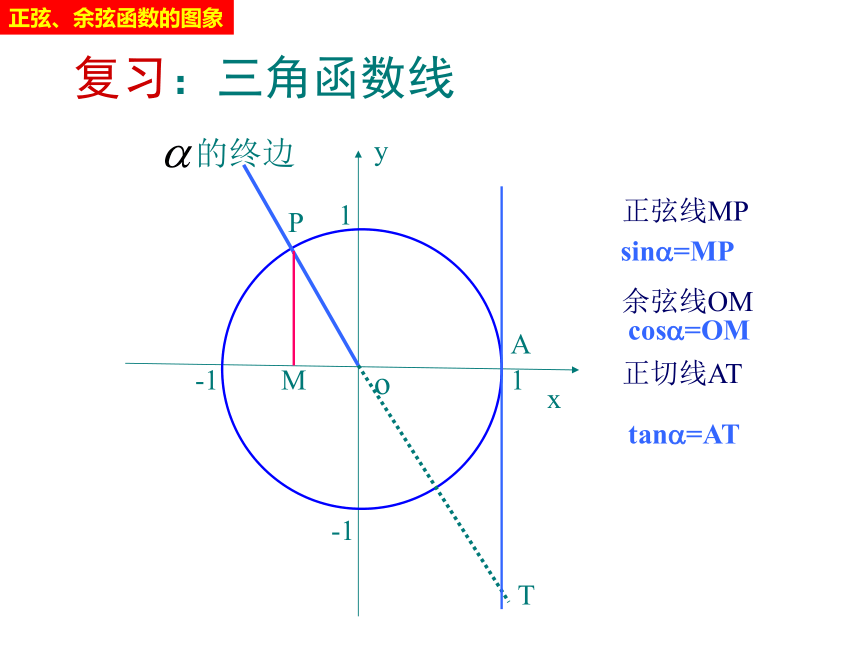
复习:三角函数线
x
y
o
P
M
T
1
A
的终边
-1
-1
1
正弦线MP
余弦线OM
正切线AT
sin?=MP
cos?=OM
tan?=AT
正弦、余弦函数的图象
正弦、余弦函数的图象
O1
O
y
x
-1
1
A
B
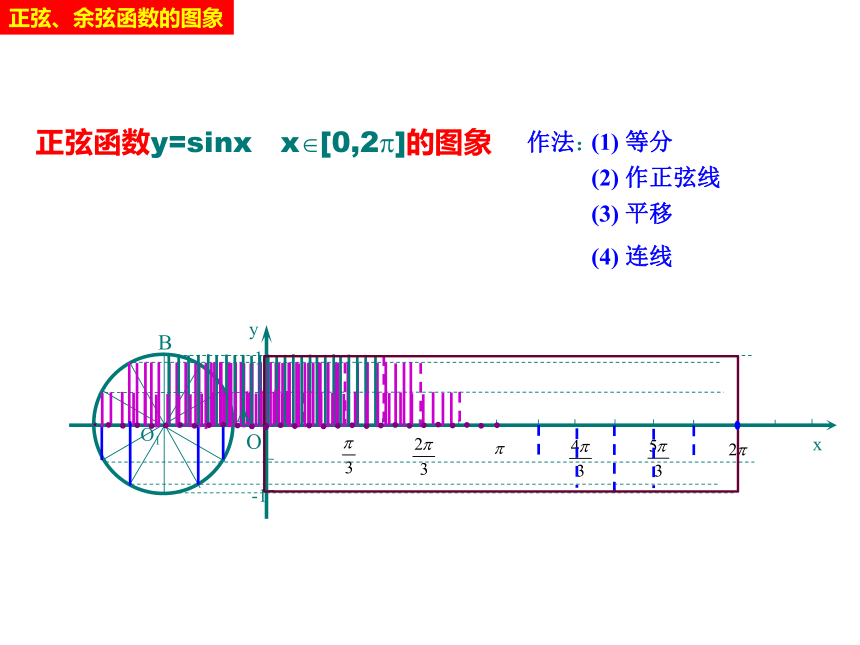
正弦函数y=sinx
x?[0,2?]的图象
(1)
等分
作法:
(2)
作正弦线
(3)
平移
(4)
连线
y=sinx
x?[0,2?]
y=sinx
x?R
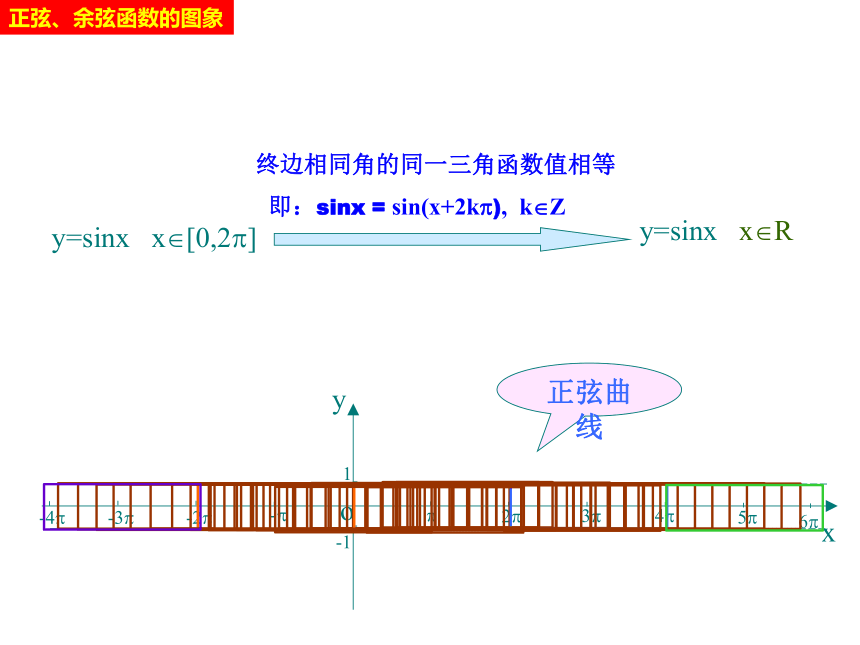
终边相同角的同一三角函数值相等
即:sinx
=
sin(x+2k?),
k?Z
正弦、余弦函数的图象
x
6?
y
o
-?
-1
2?
3?
4?
5?
-2?
-3?
-4?
1
?
正弦曲线
y
x
o
1
-1
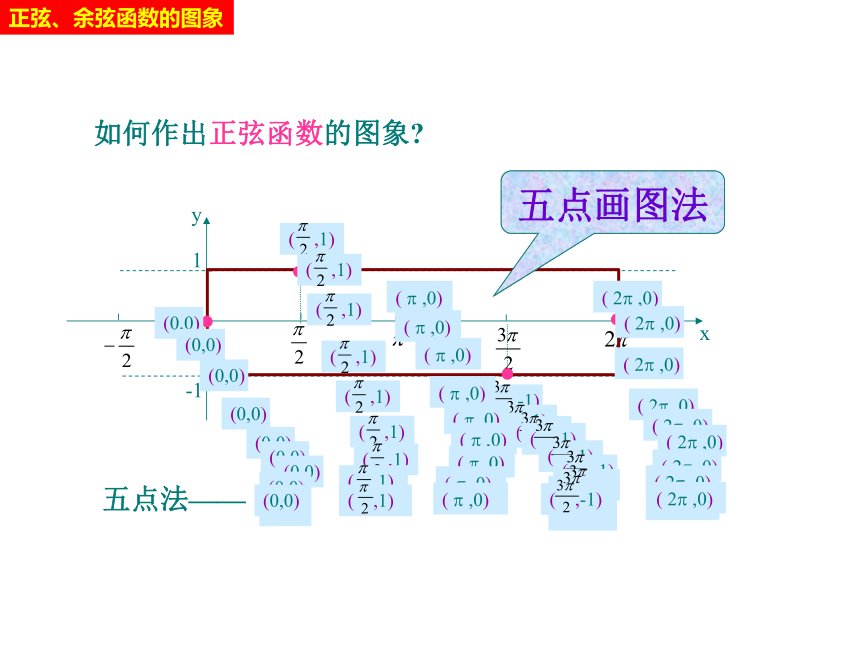
如何作出正弦函数的图象?
(0,0)
(
,1)
(
?
,0)
(
,-1)
(
2?
,0)
五点画图法
五点法——
(0,0)
(
,1)
(
?
,0)
(
,1)
(
2?
,0)
(0,0)
(
,1)
(
?
,0)
(
,1)
(
2?
,0)
(0,0)
(
,1)
(
?
,0)
(
,1)
(
2?
,0)
(0,0)
(
,1)
(
?
,0)
(
,1)
(
2?
,0)
(0,0)
(
,1)
(
?
,0)
(
,-1)
(
2?
,0)
(0,0)
(
,1)
(
?
,0)
(
,-1)
(
2?
,0)
(0,0)
(
,1)
(
?
,0)
(
,-1)
(
2?
,0)
(0,0)
(
,1)
(
?
,0)
(
,-1)
(
2?
,0)
正弦、余弦函数的图象
-
-
-1
1
-
-
-1
-
-
-
-
-1
1
-
-
-1
-
-
-
-
-1
1
-
-
-1
-
-
(1)
等分
作法:
(2)
作余弦线
(3)
竖立、平移
(4)
连线
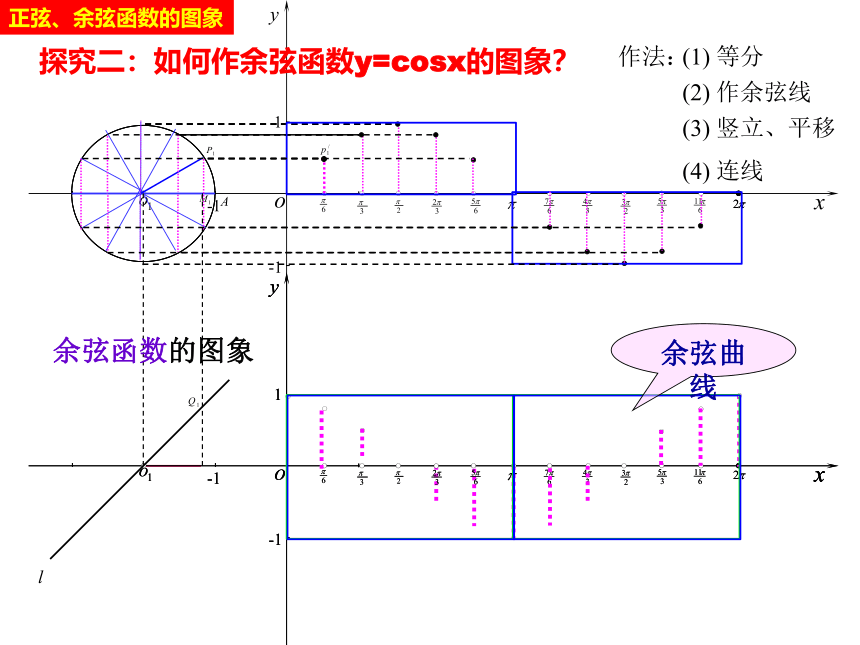
余弦函数的图象
余弦曲线
探究二:如何作余弦函数y=cosx的图象?
正弦、余弦函数的图象
因为终边相同的角的三角函数值相同,所以y=cosx的图象在……,
…与y=cosx,x∈[0,2π]的图象相同
-
-
-
-
-
-
-
-
-
1
-1
正弦、余弦函数的图象
余弦函数y=cosx,x∈R的图象
余弦曲线
-
-
-
-1
1
-
-1
正弦、余弦函数的图象
类比正弦函数如何作出余弦函数的图象?
五点法——
正弦、余弦函数的图象
与x轴的交点
图象的最高点
图象的最低点
图象的最高点
图象的最低点
(五点作图法)
与x轴的交点
x
6?
y
o
-?
-1
2?
3?
4?
5?
-2?
-3?
-4?
1
?
余弦函数的图象
正弦函数的图象
x
6?
y
o
-?
-1
2?
3?
4?
5?
-2?
-3?
-4?
1
?
y=cosx=sin(x+
),
x?R
余弦曲线
正弦曲线
正弦、余弦函数的图象
探究三:观察正弦曲线和余弦曲线有何关系?
例一:用五点法作图
(1)画出y=1+sinx
,
x∈[0,2?
]的简图
(2)画出y=cosx,
x∈[0,2?
]的简图
正弦、余弦函数的图象
思考:y=sinx与y=sinx+1图象有怎样的的关系?
x
1
2
o
?/2
?
3?/2
2?
y=1+sinx,
x?[0,2?]
.
.
.
.
.
x
cosx
-cosx
0
1
0
-1
0
1
-1
0
1
0
-1
例一:用五点法作图
(2)画出y=-cosx,
x∈[0,2?
]的简图。
正弦、余弦函数的图象
●
●
●
●
●
y=-cosx
x
[0,
]
思考:y=cosx与y=-cosx图象有怎样的的关系?
o
x
1
-1
(1)作函数
y=1+3cosx,x∈[0,2π]的简图
(2)
作函数
y=2sinx-1,x∈[0,2π]的简图
(1)
y
x
正弦、余弦函数的图象
用“五点法”画出函数y=
sinx,x?[0,
2?]的简图
用“五点法”画出函数
y=
sin2x,x?[0,
?]的简图:
令2x=X用整体替换思想
正弦、余弦函数的图象
画出函数y=
sin2x,x?[0,
?]的简图:
x
2x
sin2x
0
?
2
?
0
1
0
-1
0
y
x
o
1
-1
y=
sin2x,x?[0,
?]
正弦、余弦函数的图象
正弦、余弦函数的图象
本节课小结
本节课小结
正弦、余弦函数的图象
课后作业:用“五点法”作下面函数的图象。
正弦、余弦函数的图象
1.4.1正弦函数、余弦函数的图象
授课人:
(1).列表
(3).连线
-
-
-
-
-
-
探究一:如何做正弦函数y=sinx的图象?
正弦、余弦函数的图象
(2).描点
复习:三角函数线
x
y
o
P
M
T
1
A
的终边
-1
-1
1
正弦线MP
余弦线OM
正切线AT
sin?=MP
cos?=OM
tan?=AT
正弦、余弦函数的图象
正弦、余弦函数的图象
O1
O
y
x
-1
1
A
B
正弦函数y=sinx
x?[0,2?]的图象
(1)
等分
作法:
(2)
作正弦线
(3)
平移
(4)
连线
y=sinx
x?[0,2?]
y=sinx
x?R
终边相同角的同一三角函数值相等
即:sinx
=
sin(x+2k?),
k?Z
正弦、余弦函数的图象
x
6?
y
o
-?
-1
2?
3?
4?
5?
-2?
-3?
-4?
1
?
正弦曲线
y
x
o
1
-1
如何作出正弦函数的图象?
(0,0)
(
,1)
(
?
,0)
(
,-1)
(
2?
,0)
五点画图法
五点法——
(0,0)
(
,1)
(
?
,0)
(
,1)
(
2?
,0)
(0,0)
(
,1)
(
?
,0)
(
,1)
(
2?
,0)
(0,0)
(
,1)
(
?
,0)
(
,1)
(
2?
,0)
(0,0)
(
,1)
(
?
,0)
(
,1)
(
2?
,0)
(0,0)
(
,1)
(
?
,0)
(
,-1)
(
2?
,0)
(0,0)
(
,1)
(
?
,0)
(
,-1)
(
2?
,0)
(0,0)
(
,1)
(
?
,0)
(
,-1)
(
2?
,0)
(0,0)
(
,1)
(
?
,0)
(
,-1)
(
2?
,0)
正弦、余弦函数的图象
-
-
-1
1
-
-
-1
-
-
-
-
-1
1
-
-
-1
-
-
-
-
-1
1
-
-
-1
-
-
(1)
等分
作法:
(2)
作余弦线
(3)
竖立、平移
(4)
连线
余弦函数的图象
余弦曲线
探究二:如何作余弦函数y=cosx的图象?
正弦、余弦函数的图象
因为终边相同的角的三角函数值相同,所以y=cosx的图象在……,
…与y=cosx,x∈[0,2π]的图象相同
-
-
-
-
-
-
-
-
-
1
-1
正弦、余弦函数的图象
余弦函数y=cosx,x∈R的图象
余弦曲线
-
-
-
-1
1
-
-1
正弦、余弦函数的图象
类比正弦函数如何作出余弦函数的图象?
五点法——
正弦、余弦函数的图象
与x轴的交点
图象的最高点
图象的最低点
图象的最高点
图象的最低点
(五点作图法)
与x轴的交点
x
6?
y
o
-?
-1
2?
3?
4?
5?
-2?
-3?
-4?
1
?
余弦函数的图象
正弦函数的图象
x
6?
y
o
-?
-1
2?
3?
4?
5?
-2?
-3?
-4?
1
?
y=cosx=sin(x+
),
x?R
余弦曲线
正弦曲线
正弦、余弦函数的图象
探究三:观察正弦曲线和余弦曲线有何关系?
例一:用五点法作图
(1)画出y=1+sinx
,
x∈[0,2?
]的简图
(2)画出y=cosx,
x∈[0,2?
]的简图
正弦、余弦函数的图象
思考:y=sinx与y=sinx+1图象有怎样的的关系?
x
1
2
o
?/2
?
3?/2
2?
y=1+sinx,
x?[0,2?]
.
.
.
.
.
x
cosx
-cosx
0
1
0
-1
0
1
-1
0
1
0
-1
例一:用五点法作图
(2)画出y=-cosx,
x∈[0,2?
]的简图。
正弦、余弦函数的图象
●
●
●
●
●
y=-cosx
x
[0,
]
思考:y=cosx与y=-cosx图象有怎样的的关系?
o
x
1
-1
(1)作函数
y=1+3cosx,x∈[0,2π]的简图
(2)
作函数
y=2sinx-1,x∈[0,2π]的简图
(1)
y
x
正弦、余弦函数的图象
用“五点法”画出函数y=
sinx,x?[0,
2?]的简图
用“五点法”画出函数
y=
sin2x,x?[0,
?]的简图:
令2x=X用整体替换思想
正弦、余弦函数的图象
画出函数y=
sin2x,x?[0,
?]的简图:
x
2x
sin2x
0
?
2
?
0
1
0
-1
0
y
x
o
1
-1
y=
sin2x,x?[0,
?]
正弦、余弦函数的图象
正弦、余弦函数的图象
本节课小结
本节课小结
正弦、余弦函数的图象
课后作业:用“五点法”作下面函数的图象。
正弦、余弦函数的图象
