_1.1.2 弧度制和弧度制与角度制的换算 课件(共15张PPT)2020-2021学年高中数学人教B版必修4
文档属性
| 名称 | _1.1.2 弧度制和弧度制与角度制的换算 课件(共15张PPT)2020-2021学年高中数学人教B版必修4 |

|
|
| 格式 | ppt | ||
| 文件大小 | 4.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-01 09:33:08 | ||
图片预览





文档简介
(共15张PPT)
课程名称:弧度制和弧度制与角度制
的互化
年
级:高一年级
版
本:人教版B版
§1.1.2
弧度制和弧度制与角度制的换算
一、新课导入——复习角度制
角的终边的旋转方向
零角
负角
正角
→
正的角度数
→
负的角度数
→
0°
比如:
30°,
600°
比如:-30°,-600°
1°是如何定义的?
六十进制
一条射线绕着它的端点从一个位置旋转到另一个位置所形成的图形
任意角
角度制
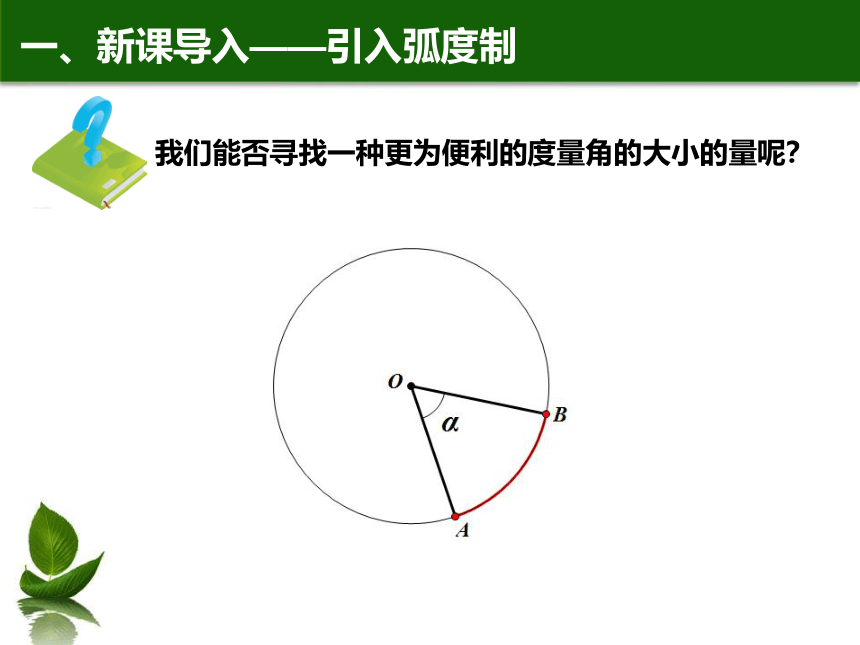
一、新课导入——引入弧度制
我们能否寻找一种更为便利的度量角的大小的量呢?
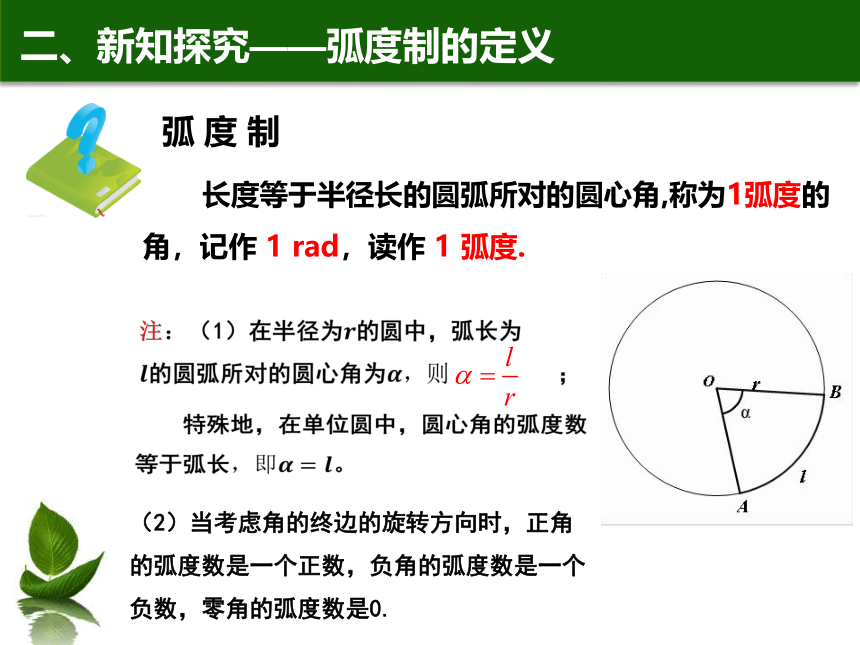
弧
度
制
长度等于半径长的圆弧所对的圆心角,称为1弧度的角,记作
1
rad,读作
1
弧度.
二、新知探究——弧度制的定义
?
?
(2)当考虑角的终边的旋转方向时,正角的弧度数是一个正数,负角的弧度数是一个负数,零角的弧度数是0.
现在对于同一个角,我们既可以用角度制来表示角,也可以用弧度制来表示.那么两者之间能够相互转化吗?360°是多少弧度?180°呢?90°呢?1°呢?
二、新知探究——弧度制与角度制的互化
由于在半径为r的圆中,360°角所对的弧长l=2πr
,于是该角的弧度数是2π,则
弧度制与角度制的互化
例1
把下列各角化为角度与弧度
二、新知探究——弧度制与角度制的互化
?
答案:
练习2
写出下列各组角度所对应的弧度
三、新知巩固——弧度制与角度制的互化
练习1
把下列各角化为角度与弧度
答案:
四、新知探究——弧长公式和扇形面积公式
?
?
弧长公式:
扇形面积公式:
练习3:(1)已知扇形的圆心角为60°,半径为3,求圆心角所对弧长及扇形面积。
五、新知巩固——弧长公式和扇形面积公式
练习3:(2)已知扇形的弧长为10,半径为5,求圆心角及扇形面积.
五、新知巩固——弧长公式和扇形面积公式
练习3:(2)已知扇形的弧长为10,半径为5,求圆心角及扇形面积.
思考:弦AB的长度为多少?
五、新知巩固——弧长公式和扇形面积公式
?
1.弧度制的概念
2.角度制与弧度制的互化
3.弧长公式、扇形面积公式
特殊角的
弧度数
六、新知小结
?
1、复习今天新学习的内容;
2、记忆特殊角的弧度数
3、作业本上完成:
课本A组习题3、5;B组习题4、5
七、作
业
The
High
School
Affiliated
to
Xi'an
JiaoTong
University
课程名称:弧度制和弧度制与角度制
的互化
年
级:高一年级
版
本:人教版B版
§1.1.2
弧度制和弧度制与角度制的换算
一、新课导入——复习角度制
角的终边的旋转方向
零角
负角
正角
→
正的角度数
→
负的角度数
→
0°
比如:
30°,
600°
比如:-30°,-600°
1°是如何定义的?
六十进制
一条射线绕着它的端点从一个位置旋转到另一个位置所形成的图形
任意角
角度制
一、新课导入——引入弧度制
我们能否寻找一种更为便利的度量角的大小的量呢?
弧
度
制
长度等于半径长的圆弧所对的圆心角,称为1弧度的角,记作
1
rad,读作
1
弧度.
二、新知探究——弧度制的定义
?
?
(2)当考虑角的终边的旋转方向时,正角的弧度数是一个正数,负角的弧度数是一个负数,零角的弧度数是0.
现在对于同一个角,我们既可以用角度制来表示角,也可以用弧度制来表示.那么两者之间能够相互转化吗?360°是多少弧度?180°呢?90°呢?1°呢?
二、新知探究——弧度制与角度制的互化
由于在半径为r的圆中,360°角所对的弧长l=2πr
,于是该角的弧度数是2π,则
弧度制与角度制的互化
例1
把下列各角化为角度与弧度
二、新知探究——弧度制与角度制的互化
?
答案:
练习2
写出下列各组角度所对应的弧度
三、新知巩固——弧度制与角度制的互化
练习1
把下列各角化为角度与弧度
答案:
四、新知探究——弧长公式和扇形面积公式
?
?
弧长公式:
扇形面积公式:
练习3:(1)已知扇形的圆心角为60°,半径为3,求圆心角所对弧长及扇形面积。
五、新知巩固——弧长公式和扇形面积公式
练习3:(2)已知扇形的弧长为10,半径为5,求圆心角及扇形面积.
五、新知巩固——弧长公式和扇形面积公式
练习3:(2)已知扇形的弧长为10,半径为5,求圆心角及扇形面积.
思考:弦AB的长度为多少?
五、新知巩固——弧长公式和扇形面积公式
?
1.弧度制的概念
2.角度制与弧度制的互化
3.弧长公式、扇形面积公式
特殊角的
弧度数
六、新知小结
?
1、复习今天新学习的内容;
2、记忆特殊角的弧度数
3、作业本上完成:
课本A组习题3、5;B组习题4、5
七、作
业
The
High
School
Affiliated
to
Xi'an
JiaoTong
University
